动态交通场景下基于时空导航地图的行驶轨迹规划方法

宋文杰，冯思源，封志奇，付梦印

（北京理工大学 自动化学院，北京 100081）

智能无人系统，是一个集自主感知理解、智能决策规划、集群协同控制等核心技术于一体的综合体，具有极高的社会和经济价值，是国家重点布局的科技方向，已成为引领新一轮科技革命和产业变革的重要战略支点。无人驾驶汽车作为智能无人系统技术最典型的市场化/社会化应用，不仅可以极大地推动车辆产品革新和产业生态变革，更是解决当前社会交通通行效率低下、道路安全问题突出、资源环境压力巨大等问题的有效途径。

无人驾驶汽车在复杂动态的城市结构化道路条件下实现安全（Safe）、平稳（Smooth）、智能（Smart）、快速（Speed）的4S自动驾驶，目前主要面临两大挑战：1. 大范围场景的高精度地图构建及精确定位定向；2. 高密度动态目标干扰下的智能决策与规划。

针对挑战1，百度、谷歌、高德等公司均已投入大量人力、物力、财力开展高精度地图构建、组合定位、地图匹配等工作，目前无人驾驶汽车在绝大多数城市环境下可实现较为稳定可靠的定位效果，具备一定商业落地条件；针对挑战2，由于环境极为多样、多类型目标运动特点极为复杂，尽管世界范围内大量研究人员已开展广泛研究，目前无人驾驶汽车在动态环境下的安全、高效、智能决策与规划仍是一项重要难题，其自动驾驶水平与人类仍不具备可比性（或可替代性）。因此，高密度动态交通场景下实现4S标准的智能决策与规划是自动驾驶功能的瓶颈技术，也是无人驾驶汽车体现其智力水平的一项重要指标。

为克服上述挑战2，现有方法通常在二维行驶空间中搜索出一条无碰撞参考路径，再将时间约束信息加入到参考路径中，经过反复迭代，寻找出一条符合要求的轨迹。其中，最优化方法[1]通过在多组约束（如车辆横向和纵向限制、环境限制、曲率限制等）下最小化性能指标（动能变化、加加速度、横向加速度），以获得平滑的驾驶轨迹[2]。Dieter Fox[3]提出的动态窗口法（Dynamic Window Approach）可以有效解决移动机器人的避障问题；斯坦福大学开发的自动驾驶汽车Junior在DARPA城市挑战赛中成功展示了基于最优控制的轨迹规划技术的有效性[4]。但此类方法往往会增加算法的时间复杂度且难以应用于速度和路径高度耦合的高密度动态交通场景。

在Frenet[5]框架中，路径-速度解耦法是目前常用的最优化方法之一，主要是分别优化路径和速度：路径优化主要考虑静态障碍物；然后基于生成的路径，结合动态目标以优化速度[6]。Zhan[7]等人通过沿着粗略参考路径的纵向和横向对运动规划进行空间划分，结合A*搜索和二次规划进行粗略长期纵向运动和短期轨迹规划；但该方法依然是对空间横纵向的分解规划，虽然降低了规划问题的计算复杂度，但由于缺乏时间维度信息，存在一定局限性。百度Apollo EM planner[5]将高维的轨迹规划解耦：路径优化框架利用ST图[8]进行无碰撞轨迹规划；速度优化框架用来评估路径优化器中车辆与低速障碍物的交互性，然后速度优化器接到生成的轨迹并求解最优速度。该类方法通过将时间与空间解耦，分别求解轨迹与速度，在一定程度上可以有效解决复杂交通场景下动态车辆扰动问题。

与上述思路不同，一些研究人员将时间和空间维度统一到同一坐标系进行轨迹规划，以解决动态场景时空耦合问题。Ding等人[9]提出了一种新的统一时空语义走廊结构，为不同类型的语义提供一个抽象层次元素；该系统通过正向推演的模拟模型从预测行为中采样得到种子点，依次膨胀出一系列相互连接的无碰撞立方体，并在时空域内由语义元素构成动态约束，利用分段Bezier曲线参数化的凸包和速度图特性进行二次规划，但该方法在时空走廊的种子点选取和时间分配等方面并未进行明确阐述。

由此可见，在高动态结构化道路高速自动驾驶场景中，无人驾驶汽车周围运动的障碍物会在其规划空间中引入时空约束。因此实现安全、平稳的自主规划必须解决时空解耦问题，以在时空约束条件下搜索一条最优平滑时空轨迹。本文基于实时车路状态反馈信息（从高精度地图获得道路状态，从感知模块获得周围实时动态目标状态），以无人驾驶汽车为第一视角，通过多目标行为预测等手段，构建三维时空导航地图；通过增加时间维度，将静态障碍物和动态障碍物统一到同一参数空间中。基于该参数空间，通过前端A*路径搜索初始化均匀B-样条曲线控制点，设计轨迹代价函数，进行非线性优化，生成一条符合安全无碰撞和车辆运动约束（速度、加速度限制）的时空轨迹，从而将二维Frenet动态物理空间下决策与规划问题转化为三维时空下静态场景决策与规划问题，有效降低多目标运动对无人驾驶汽车决策与规划引入的扰动。

1 基于时空导航地图的轨迹优化方法系统

本文所述算法系统如图1所示，主要包含时空导航地图构建、前端路径搜索和基于B-样条曲线的轨迹优化三个模块。首先，根据感知模块的主车状态信息（其中包括位置、速度、方向等）、周围动态车辆的运动信息以及道路结构信息，通过对周围动态车辆进行轨迹预测，构建Frenet坐标系下（s,d,t）局部三维时空占据栅格地图，并构建欧式符号距离场（Euclidean Signed Distance Fields, ESDF）[10]。在基于本团队已完成的车道时空间隙决策[11]下（综合分析道路交通情况，构建车道时空间隙决策拓扑，选择最优决策拓扑路径作为无人驾驶汽车的实时决策结果，主要用于指导无人驾驶汽车是否变道、以及如何变道（依次通过哪些间隙），由于本部分非本文重点，此处不展开详细介绍），对决策间隙进行局部目标点选取和A*路径搜索，得到栅格路径。将栅格路径点进行采样作为B-样条曲线的初始控制点，并且构建均匀B-样条曲线，基于欧式符号距离场对控制点进行非线性优化，得到符合车辆运动学约束的行驶轨迹。

图1 基于时空域地图的轨迹优化方法系统框图Fig.1 System block diagram of trajectory optimization method based on spatio-temporal map

2 基于时空导航地图的轨迹生成与优化

2.1 时空导航地图构建

在机器人领域，常用地图种类主要包含尺度地图（Metric Map）、拓扑地图（Topological Map）以及语义地图（Semantic Map）。在轨迹规划方面，常用的为尺度地图，即地图中每一点对应于一个坐标。占据栅格地图（Occupancy Grid Map）[12]是将场景按照一定距离进行划分，得到的一种结构化地图，在占据栅格地图中，对于一个点，存储的是障碍物占据概率。对每个栅格点直接的存储方式带来的好处是坐标索引查询复杂度低至O(1)（无论数据规模多大，都可以在一次计算后找到目标），但较高的地图分辨率也将导致内存占用较大和更新延迟。而八叉树地图（Octo-map）[13]是对占据栅格地图存储方式的一种改进，环境中没有障碍物的空间，用大方块表示，当大方块里面有障碍物时，便进行递归切分，直至寻到完整包含障碍物的最小方块为止。该方法所构建的地图为稀疏地图，并且在查询过程中是非直接查询。

在高速道路环境下，车辆不进行任何倒车操作，因此本文方法所采用的局部地图在Frenet坐标系下，仅考虑了无人驾驶汽车前方50米范围区域，所包含时间维度范围为0～5 s。

如图2-3所示，将车辆感知结果映射到局部坐标系，主车位置始终保持固定（图3中黑色标记）。

图2 高速场景仿真环境Fig.2 The high-speed scene simulation environment

图3 高速场景环境构建时空域地图Fig.3 Constructing spatio-temporal maps in high-speed scenarios

由于本文重点不包括车辆轨迹预测，因此对于周围动态车辆，我们研究采用线性预测的方法对周围车辆进行运动状态估计，从而得到如图3所示的三维空间占据栅格地图，地图分辨率为0.02 m。时间维度从当前时刻至未来5 s，以推测5 s内周围车辆的运动分布，车辆速度的不同呈现为占据栅格点在时间轴正方向上斜率的不同。如图2所示，车辆1相比于车辆4的速度较大，则在图3中车辆1的栅格点序列沿时间轴斜率更大。

三维占据栅格的作用在于为前端路径搜索模块提供可行的搜索空间，而针对后端轨迹优化模块，为确保轨迹的安全可行，需要对轨迹的控制点进行位置约束，其中包括距离障碍物的距离。由于三维占据栅格地图无法直接提供距离信息，本文通过构建三维空间中的欧式符号距离场，描述三维空间中任意点距离障碍物的距离信息，并对障碍物进行距离和梯度信息查询。欧式符号距离场的应用对机器人的在线运动规划具有重要意义。Han等人[14]于2019年提出FIESTA地图系统，增量式地建立ESDF地图。FIESTA系统通过引入两个用以插入和删除障碍物的独立更新队列，使用索引数据结构和双向链表进行ESDF地图维护，实现在广度优先搜索算法框架下，更新尽可能少的地图节点。如图4所示，右侧为三维空间中t= 0, 1, 2, 3, 4 s时的ESDF地图。其中主车位于第三车道，根据构建的ESDF地图可快速获取任意一点处距离障碍物的距离信息，以用于后端轨迹优化。

图4 构建欧式距离场ESDFFig.4 Build ESDF map

2.2 时空地图中方向限制的A*路径搜索

基于三维时空地图构建和本团队已完成的时空间隙决策算法[11]，可以获得三维空间中局部目标点g（s,d,t）和三维占据栅格地图。然后，采用A*搜索算法对主车节点到目标点的路径进行搜索：其中采用的启发函数为欧式距离函数，描述为当前节点距目标点的欧式距离d。如图5所示（针对图4所示场景），在高速道路行驶过程中，车辆行驶不能掉头、倒车，因此在进行路径搜索中，限制搜索方向为s和t维度的正方向，减少搜索过程中的访问节点数，缩短A*搜索时间。

图5 三维时空导航地图下前端A*路径搜索结果Fig.5 Front-end A* path search results under the three-dimensional spatio-temporal navigation map

2.3 基于B-样条曲线的轨迹优化

2.3.1 B-样条曲线

B-样条曲线是B-样条基函数（给定区间上的所有样条函数组成一个线性空间）的线性组合，如图6-7所示。

图6 四阶B-样条曲线Fig.6 Fourth-order B-spline curve

设有{Q0,Q1…QN}共有N+1个控制点，一个节点向量U= {u0,u1…um}，用于定义k阶（k-1次）样条曲线，其中必须满足k≥1、m=N+k，则k阶样条曲线的定义如下：

式中，Bi,k(u)为第i个k阶B-样条基函数，与控制点Qi相对应，定义如下：

B-样条轨迹可由时间t参数化，其中t∈ [tk,tm-k]。对于均匀B-样条曲线，每个节点跨度 Δtj=tj+1-tj的值Δt是相同的。因此，对于局部起始点（s0,d0,t0）和局部目标点（sg,dg,tg），定义节点跨度为Δt= (tg-t0)/(m+1)。

B-样条曲线具有凸包性质：样条曲线会被包含于控制点构成的凸包内（图6）；并且，样条曲线一阶微分仍为B样条曲线（图7）。在轨迹优化过程中这些性质被广泛应用[15,16]，以确保轨迹的动态可行性和行驶安全性。B-样条曲线的阶数越高，曲线的导数次数也越高，产生更多零点，导致原曲线存在较多极值；相反，阶数越低，样条曲线逼近控制点的效果越好。四阶（三次）B-样条曲线能够实现二阶导数连续，因此，本文选择四阶B-样条曲线用于轨迹优化。针对动态可行性，对曲线进行一阶和二阶微分即可得到速度与加速度曲线，二者同样具备B-样条曲线特性，其控制点分别为{V0,V1…VN-1}和{A0,A1…AN-2}，限制速度与加速度为Vi∈[ -vmax,vmax]，Ai∈[ -amax,amax]。其中Vi和Ai计算如下：

图7 B-样条曲线的一阶微分Fig.7 The first derivative of the fourth-order B-spline curve

2.3.2 控制点非线性优化

针对由N+1个控制点{Q0,Q1,… ,QN}定义的四阶B-样条曲线，由于轨迹初始状态与末端状态固定，需对初始和末端的位置、速度、加速度进行限制，故设置{Q0,Q1,Q2,QN-2,QN-1,QN}为固定值，优化的控制点为{Q3,Q4,… ,QN-3}共N-5个。

设计如下的代价函数：

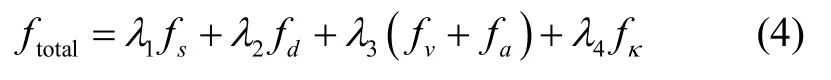
其中，fs为平滑度代价函数，fd为距离代价函数，fv和fa分别表示速度和加速度代价函数，fκ表示曲率代价函数，1λ、2λ、3λ、4λ为相应的权重参数。

通过轨迹的几何信息来定义平滑度代价函数fs，代价定义如下[17]：

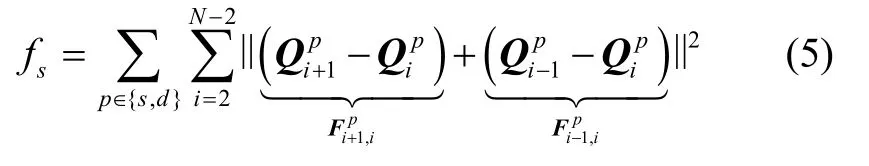
距离代价函数定义如下：

其中，d（Qi）表示控制点Qi到最近障碍物的距离值（该值通过欧式距离场ESDF获取），dsafe表示安全距离阈值，设置dsafe= 3m。

为将速度与加速度约束于规定范围内，对超出最大允许值vmax、amax的速度和加速度进行惩罚，超速评估函数设计如下：

其中p∈{s,d}，超加速度评估函数形式与之相同。基于二者，定义速度和加速度代价函数fv和fa以惩罚速度和加速度不可行的控制点，形式如下:

曲率代价函数定义如下：

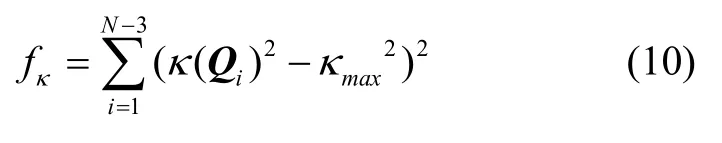
其中κ(Qi)表示Qi处曲率，进行轨迹曲率代价计算时需转换为笛卡尔坐标系。

图8展示了样条曲线优化结果。首先对A*搜索得到的路径点进行采样得到初始控制点，并进行时间均匀分配得到均匀样条曲线（图8中黄色轨迹）。利用Nlopt开源非线性优化库中的NLOPT_LD_TNE WTON算法[18]对式(4)的优化问题进行求解，得到优化后的轨迹（图8中绿色轨迹）。

图8 B-样条曲线优化结果Fig.8 B-spline curve optimization results

3 仿真试验与分析

本部分主要展示并分析时空域地图中的轨迹优化结果，验证所提出算法的有效性。在进行局部轨迹优化过程中，构建局部时空域导航地图，并先后进行前端路径搜索与后端轨迹优化。

首先分析系统框架中各个模块耗时情况，如表1所示。对无人驾驶汽车驾驶过程中所有车辆的行驶方向进行假设，即假设车辆只能沿道路前向行驶，对A*搜索方向进行限制，缩小了搜索空间，使搜索平均耗时由12.20 ms减少至8.80 ms，效率得到提升。整个轨迹优化过程平均耗时为51.27 ms，满足无人驾驶汽车行驶要求。

表1 时空域轨迹规划仿真实验耗时Tab.1 Time-consuming simulation experiment of trajectory planning under spatio-temporal map

图9-12分别展示了在简单车道保持场景和复杂变道场景下时空域轨迹规划的仿真试验界面和数据分析结果。如图9-10所示，在保持车道场景下，主车（无人驾驶汽车）的速度、加速度以及曲率都在车辆运动约束范围之内。由于主车前方有其他车辆，因此在保持车道的过程中，可以看到主车规划结果有适当减速，以保持安全距离。图11中换道场景随即发生在图9场景之后，相比之下，主车速度与加速度发生较大变化，在换道过程中主车稍微加速进行换道，换道完成后重新进行车速调整。并且在换道过程中势必引起车辆曲率变化，如图12所示，换道成功后轨迹曲率减小。

图9 车道保持场景仿真界面Fig.9 Lane-keeping scene simulation interface

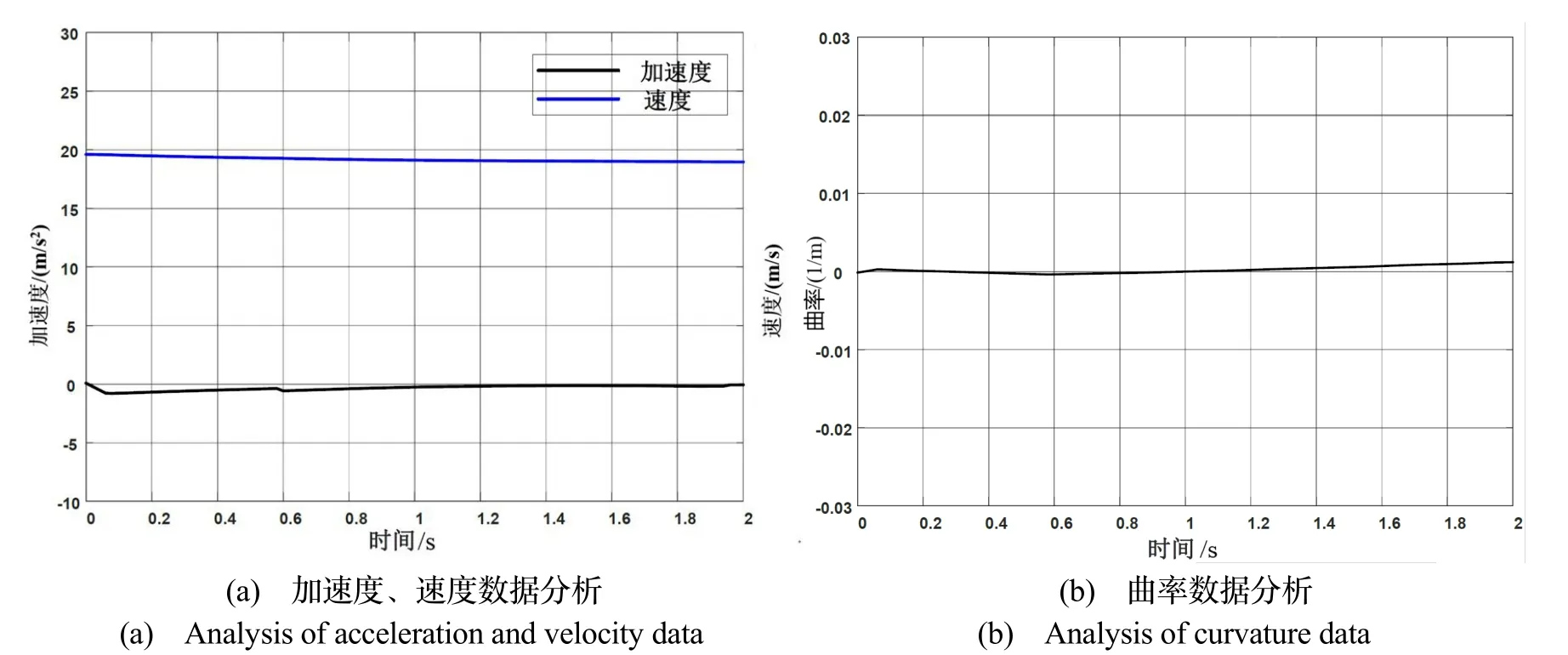
图10 车道保持场景轨迹优化结果分析Fig.10 Analysis of the trajectory optimization results of the lane-keeping scene

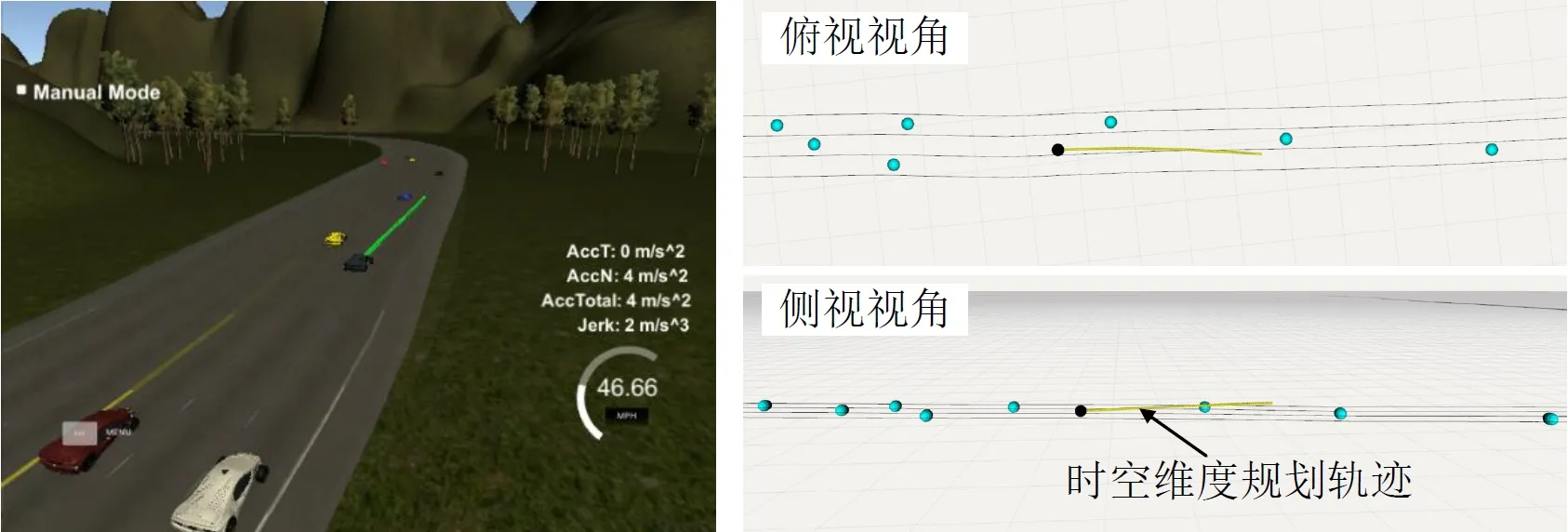
图11 换道场景仿真界面Fig.11 Lane-changing scene simulation interface

图12 换道场景轨迹优化结果分析Fig.12 Analysis of the trajectory optimization results of the lane-changing scene

4 结 论

针对高动态结构化道路自动驾驶需求，本文提出了一种基于时空导航地图的轨迹优化方法，在时空约束条件下提高车辆行驶轨迹质量，解决了高速场景下静动态障碍物统一表征问题，提高了轨迹平滑度。该方法引入时间维度作为参考，将感知结果投影至三维时空地图，构建欧氏距离场，针对决策目标先后进行路径搜索与轨迹优化。同时，通过限制A*路径搜索方向，缩小搜索空间，加快搜索效率，用A*路径初始化均匀B-样条曲线控制点，设计轨迹代价函数，进行非线性优化，生成最优轨迹控制点。仿真试验结果表明，所提出的方法在车道保持场景以及换道场景下均能有效生成符合车辆运动约束的平滑轨迹，在4S驾驶标准上符合人类驾驶特性。