光纤环混合四极对称绕制方法

范运强，魏 伟，黄继勋，李 晶

（1. 北京航天时代光电科技有限公司，北京 100094；2. 空军装备部驻北京地区第四军事代表室，北京 100041；3. 北京航天控制仪器研究所，北京 100854）

光纤陀螺是一种基于Sagnac效应的全固态陀螺仪，具有抗冲击、灵敏度高、寿命长、动态范围大、启动时间短等优点[1]，已在海、陆、空、天等领域得到广泛应用[2]。光纤陀螺易受环境温度影响，造成光纤陀螺零偏发生漂移，这种由温度变化引起的零偏误差被称为Shupe误差[3]，该误差的存在也成为制约高精度光纤陀螺工程应用的主要技术瓶颈之一。

光纤环是光纤陀螺的敏感核心，其性能直接影响光纤陀螺温度性能，而光纤环温度性能受绕制方法的影响较为明显，优化光纤环绕制方法可有效提升光纤环温度性能，是提升光纤陀螺温度性能的一个主要途径[3]。四极对称绕制方法的提出，使Shupe误差减小了3个数量级[2,3]；八极对称绕法和十六极对称绕法是基于四极对称绕法衍生出的绕制方法，对进一步抑制光纤陀螺温度误差效果显著[1,4]，但温度误差仍存在残余，这种残余误差对高精度光纤陀螺来说依然较大；交叉绕法相对四极对称绕法具有更明显的温度误差抑制效果，温度误差能降低1个数量级[4]，但该方法中光纤绕制端的切换以及随动放纤结构换位均在光纤环层中间位置，每个四极内需进行2次光纤绕制端切换和2次随动放纤结构位置切换，同时引起两端光纤出现2次交叉，因交叉造成的光纤凸起将直接影响上层光纤的绕制，同时绕制端切换、随动放纤结构位置切换过于频繁，导致工艺过于复杂，实现难度较大，未能在工程中大范围推广应用。而工程实践迫切需要一种工艺方法简单、温度误差抑制效果理想的绕制方法，因此仍有必要对光纤环绕制方法开展深入研究。

本文以光纤陀螺温度误差原理为基础，对光纤环温度误差以匝为单位进行了离散化定量分析，根据正负四极对称绕法对温度误差的影响相反的特征，在考虑工程实现难度和温度误差抑制效果的同时，提出了基于现有工艺方法和设备的混合四极对称绕制方法，验证了在众多混合四极对称绕法中存在最优绕法，并对其中两种混合四极对称绕法的效果进行了验证，结果显示混合四极对称绕法抑制光纤环温度误差的效果更好。

1 光纤环Shupe误差理论分析

1.1 光纤环Shupe误差模型

光纤折射率受温度影响明显，而光波在光纤中传播所产生的相位延迟与光纤折射率大小直接相关，当光纤环非中点处光纤受到温度干扰时，折射率发生变化，光纤环内部相向传输的两束光波经过该点的时间不同，经过该点所产生的相位延迟不一致，由此引起的零偏误差大小可表示为：

式中， ΔΦE（t）为t时刻温度变化引起的陀螺相位误差，为光波的传播常数，c为光波在光纤中的传播速度，为光纤纤芯折射率温度系数，z,t）为t时z点处光纤纤芯温度变化率，L为光纤陀螺光路总长度。

将式(1)按照中点对称的方式进行展开：

若光纤环共有m个四极，假设相邻两层间的光纤长度差为定值Δl，光纤中点两侧各层间对称性分布如图1所示，光纤环绕制时随绕制层数增加，光纤绕制直径变大，每层光纤绕制的长度逐层增加。

图1 光纤环层间对称分布Fig.1 Symmetric distribution of fiber coil in layers

光纤环每个四极内两端光纤长度相等，因此可将光纤环的温度误差以四极为单位进行离散化展开，此时式(2)可表示为：

式中，li_s为光纤上半段第i个四极内积分起点，li_e为光纤上半段第i个四极内积分结束点。

以上半段作为计算基准，将公式每个四极内的温度误差以匝为单位进行展开，此时式(3)可变为：

式中，N为每层匝数；li_1_j_s和li_1_j_e分别为光纤环第i个四极内第1层第j匝积分的起点和终点；li_4_j_s和li_4_j_e分别为光纤环第i个四极内第4层第j匝积分的起点和终点分别为第i个四极内第1层第j匝的温度变化率和与该匝光纤距中点对称的光纤的温度变化率；和分别为第i个四极内第4层第j匝的温度变化率和与该匝光纤距中点对称的光纤的温度变化率。

每层光纤的直径不同，不同层间每匝光纤的长度也存在差异，第i个四极内以匝为单位的光纤对称分布情况如图2所示。每个四极内，与第1层第1匝对称的光纤分布在第2层第1匝，而与第1层第j（2≤j≤N）匝对称的光纤则分布在第2层的第j-1匝和第j匝，其中分布在第2层第j-1匝内的光纤长度为2π(j-1)d（d为光纤直径）；与第4层第j（1≤j＜N）匝对称的光纤分布在第3层的第j匝和第j+1匝，其中分布在第j+1匝的光纤长度为2πjd，而与第4层第N匝对称的光纤分布在第2层第N匝和第三层第N匝，且分布在第2层第N匝的长度为2πNd。

图2 光纤环匝间对称分布Fig.2 Symmetric distribution of fiber coil in turns

根据光纤环对称分布情况，将式(4)中积分按匝分布展开，则光纤环温度误差可表示为：

式中，li_1和li_4分别表示第i个四极第1层和第4层每匝光纤的长度。

由式(5)中误差积分公式，可得光纤环温度误差的离散方程为：

式(6)为光纤环Shupe误差计算模型，利用该公式便可求出光纤环温度误差。

1.2 光纤环温度分布模型

光纤环由光纤精密绕制，并由固化胶将各匝光纤粘接固定而成，光纤环内部光纤和固化胶按一定规则均匀分布，因此可将光纤环内部热传导等效为均匀介质的热传导过程。

根据热扩散基本原理，当环境温度发生变化时，光纤环内部的热传导方程可表示为[2]：

式中，K=r/ρc′为光纤环热扩散系数，r为光纤环的导热系数，ρ为光纤环密度，c′为光纤环比热容，T0为环境初始温度，因此t时刻扩散深度为x的温度分布为：

选取某型号光纤环为研究对象，对光纤环的温度误差进行分析，其中光纤为135 μm型光纤，光纤长度1235 m，光纤环内径75 mm，外径89 mm，光纤环高度12.8 mm，光纤环层数52，每层光纤匝数91，光纤环物理参数如表1所示[9]。

表1 光纤环物理参数Tab.1 Fiber coil physical parameter

将光纤环放置在密闭的磁屏蔽工装内，通过温箱控制环境温度，测试温度范围-40℃～60℃，温度变化率1℃/min，在-40℃保温3 h，以高温60℃为起点，温度曲线如图3所示。

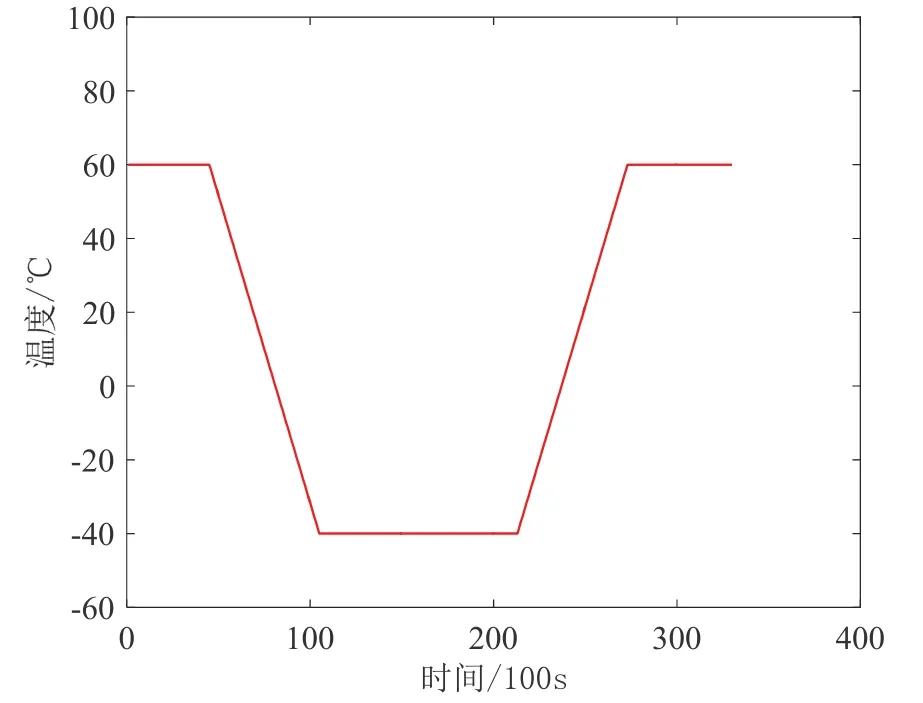
图3 温度曲线Fig.3 Temperature curve

按上述条件对光纤环磁屏蔽工装施加温度，光纤环内部热传导可分为轴向和径向两个方向，根据光纤环温度扩散原理，光纤环径向各层间温度变化和轴向各匝间温度变化分别如图4和图5所示。

图4 光纤环层间温度Fig.4 Fiber coil temperature distribution in radial direction

图5 光纤环径向温度Fig.5 Fiber coil temperature distribution in axial direction

2 混合四极对称绕法对Shupe误差的影响

2.1 正负四极对称绕法温度误差特征

光纤环常用的绕制方式为四极对称绕制，现对四极对称绕法做如下定义：由0端光纤绕制第1层和第4层，L端光纤绕制第2层和第3层的四极对称绕制方式定义为正四极对称；由L端光纤绕制第1层和第4层，由0端光纤绕制第2层和第3层的四极对称绕制方式定义为负四极对称，由正四极对称和负四极对称共同构成的绕制方式定义为混合四极对称。

当光纤环由正四极对称绕制变为负四极对称绕制时，距中点对称的光纤温度发生了转换，此时式(3)中温度误差可表示为：

由式(3)(7)知，改变光纤绕制顺序，温度误差大小不变，但随温度变化率相关性发生改变。

为验证正负四极对温度误差的影响，以正四极和负四极分别绕制一只同型号光纤环，并以图3中温度条件分别进行温度性能测试，测试曲线如图6所示。

图6 正负四极对称光纤环测试曲线Fig.6 Positive and negative quadrupole symmetric fiber coil test curve

2.2 混合四极对称绕法对Shupe误差的抑制

当光纤环采用以四极对称为单位的混合四极对称绕制时，每个四极均可采用正四极对称或负四极对称绕制，对于层数为4m的光纤环，其混合四极对称绕制的光纤环共有2m种绕制方法，将数字转换成m位二进制，以每位数字表示一个四极的绕法，数字1表示正四极，数字0表示负四极，高位表示外层四极低位表示内层四极，则表1中光纤环共有8192中绕制方法，0～8191每个数字均代表一种绕法，其中0和8191分别表示正负四极对称、5461和6553分别表示正八极和正十六极对称。

光纤环共有2m种绕制方法，若以绕法为变量，以光纤环升降温极差作为误差函数，误差值相邻的绕法的温度误差比较接近，因此可将光纤环误差函数近似看做连续函数。由正负四极对称绕法的温度特征知，正四极对称（2m）和负四极（0）对称分别为误差函数的极大值和极小值，且这两种绕法下的温度误差正负号相反，因此光纤环温度误差函数必过零点，即必然存在一种或几种绕法，使得光纤环温度误差近似为零。

选取表1中光纤环作为研究对象，利用式(6)对混合四极对称绕制的光纤环温度误差进行仿真分析，从众多混合四极对称绕法中选取一种对温度误差抑制效果相对较好的绕制方法（2235），记为混合四极对称1，其温度误差仿真结果与正四极对称、正十六极对称温度误差仿真结果如图7所示。

图7 光纤环不同绕法温度误差仿真Fig.7 Fiber coil temperature error simulation with different winding methods

以混合四极对称1与常用绕制方法分别进行光纤环绕制，并对各光纤环进行全温测试，光纤环表面温度曲线如图8所示，温度误差测试曲线如图9所示。

图8 温度测试曲线Fig.8 Temperature test curve

由图9中5组测试曲线知，采用正四极对称绕制时，光纤环温度误差与温度变化率正相关，部分四极由正四极变为负四极时（如正十六极对称），光纤环温度误差将逐渐减小，当负四极数量满足一定条件时（如负十六极对称），温度误差与温度变化率变为负相关，因此，必然存在一种或几种绕法，使两者相关性处于临界状态，此时光纤环温度误差将显著减小，光纤环温度误差与温度变化率无明显相关性。

图9 光纤环不同绕法温度误差测试曲线Fig.9 Fiber coil temperature error test curve with different winding methods

图9中光纤环实测曲线与图7中仿真曲线形状之所以存在差异，是因为仿真分析时，光纤环内部热传导模型是按等效均质理想模型计算的，而光纤环是由光纤和固化胶构成的混合物，两者存在一定差异，此外实测条件下由于受光纤环外防风罩的影响，光纤环实际热传递比理想情况缓慢，工程实践中光纤环也表现出明显的延迟特征[2]，因此实测曲线的上升和下降段曲线比较缓慢，造成理论曲线与实测曲线形状存在一定差异。

3 实验验证

根据光纤环误差机理知，在众多混合四极对称中，存在最优绕法，图9中混合四极对称绕制方法1绕制的光纤环温度误差与温度变化率依然成正相关，在该绕法的基础上增加负四极的权重可再次降低光纤环温度误差，因此，将部分内侧负四极变为正四极，同时外侧相同数量的正四极变为负四极，以此增加负相关温度误差的权重，得混合四极对称绕制方法2（1239）。

以混合四极对称1、混合四极对称2和正十六极对称对表1所示型号的光纤环分别绕制5只，并进行温度性能测试，在无温度补偿下各光纤环零偏稳定性（100 s，1 σ）如表2所示。

表2 光纤环零偏稳定性测试结果Tab.2 Fiber coil bias stability test results

表2中，采用正十六极对称绕制的5只光纤环，其全温零偏稳定性均值为0.271 °/h，采用混合四极对称1绕制的5只光纤环，其全温零偏稳定性均值为0.0241 °/h，采用混合四极对称2绕制的5只光纤环，其全温零偏稳定性均值为0.0161 °/h。与正十六极对称绕制相比，两种混合四极对称绕制的光纤环温度性能均得到明显提升，其中混合四极对称1绕制的光纤环温度性能提升了11%，混合四极对称2绕制的光纤环温度性能提升了41%，通过数据分析知，调整正负四极对称绕法的组合方式，光纤环温度误差也将随之改变，因此，采用适合的混合四极对称绕法能有效抑制光纤环温度误差。

4 结 论

根据光纤陀螺温度误差产生的机理，将光纤环温度误差以匝为单位进行了离散量化分析，建立了以匝为单位的温度误差计算模型，提出了混合四极对称的绕法，证明了存在一种或多种混合四极绕法能使光纤环温度误差显著减小，以仿真分析和实验修正的方式确定了混合四极对称1和混合四极对称2两种绕法，并对两种绕法与正十六极对称绕法进行了实验对比验证。结果表明采用混合四极对称绕制方法抑制光纤环温度误差的方法可行，且混合四极对称2更接近该工艺状态下的最优绕法。工程实践中，光纤环受设备、光纤、固化胶、绕制工艺等多个因素的影响，同一型号的光纤环在不同工艺参数下的温度性能不同，因此其最优绕法不唯一，不同工艺状态下光纤环存在不同的最优绕法。