基于K折交叉验证的SVM隧道围岩分级判别①

汪学清，刘 爽，李秋燕，马凯彬

（1.中国矿业大学（北京）力学与建筑工程学院，北京100083；2.齐齐哈尔大学建筑与土木工程学院，黑龙江齐齐哈尔161006；3.河南开放大学建筑工程与智能建造学院，河南 郑州450000）

隧道围岩分级判别是正确进行隧道设计和施工的基础，通过对围岩分级判别，可以科学管理隧道施工以及正确评价经济效益。符合工程项目实际情况的围岩分级对改善地下工程结构设计、发展新的隧道施工工艺、降低工程造价具有十分重要的意义［1］。目前国内对于隧道围岩分级常用的方法有RMR围岩分类方法［2］、距离判别分析［3］、模糊信息分析［4］、系统聚类分析［5］、灰色聚类评估法［6］和贝叶斯判别法［7］等。这些分类判别方法确定的指标大多数是在岩层揭露后勘测获得，导致围岩分级判别缺乏预见性。TSP303系统（tunnel seismic prediction system）［8］能够预先获得前方150～200 m地质数据，将这些数据与判别方法相结合为隧道围岩分级提供了一种新途径。在样本量较少时，很多学者没有重视样本划分对分类结果产生的影响，只选用1组样本训练模型，存在对样本信息利用不足的问题，导致分类结果可靠性较低。采用K折交叉验证方法，在训练样本分组后对模型交叉训练并验证，使分类结果更接近真实值。

本文根据TSP303系统确定判别指标，选取了40组样本对模型进行训练、10组样本进行测试，采用K折交叉验证法（KCV）对训练样本进行分组，代入支持向量机（SVM）分类器中进行交叉验证，确定分类器的权重，建立基于K折交叉验证的SVM（KCV⁃SVM）隧道围岩分级判别模型。分别与系统聚类分析方法、贝叶斯判别法进行对比，结果表明KCV⁃SVM模型准确率较高，可以更好地进行隧道围岩分级判别。

1 基本原理

1.1 K折交叉验证

交叉验证［9］是用来验证分类器性能的一种统计分析方法。基本思想是将原始数据进行分组，一部分作为训练集，另一部分作为验证集，首先用训练集对分类器进行训练，再利用验证集来测试训练得到的模型，以此作为评价分类器的性能指标。

K折交叉验证（KCV）［10］将原始数据分成K组，不重复地抽取1个子集作为一次验证集，将其余的K-1组子集数据组合在一起作为训练集，如图1所示，本文选取10折交叉验证法。

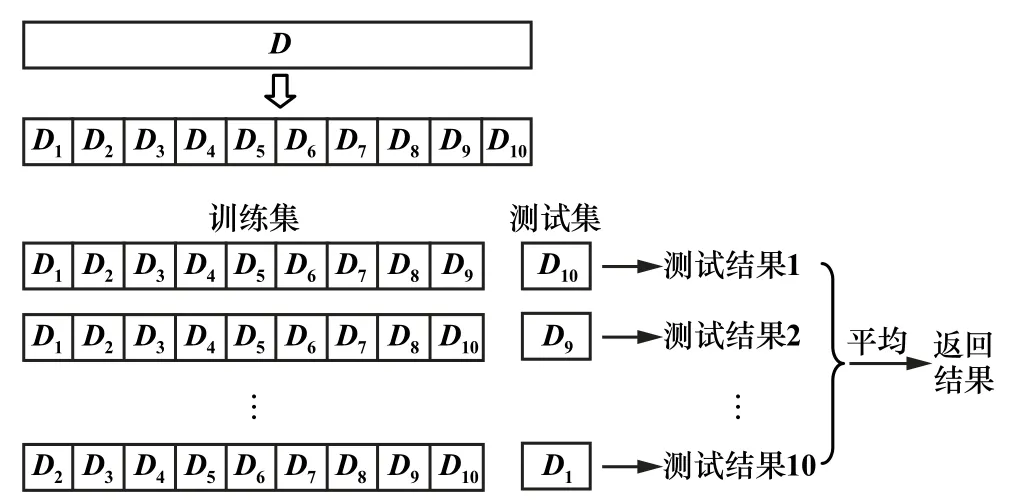
图1 10折交叉验证原理

通过分组训练会得到K个模型，用这K个模型验证集准确率平均数作为K折交叉验证分类器的性能指标［11］。K折交叉验证能避免过学习和欠学习状态的发生，最后得到的结果也比较具有说服性。

1.2 支持向量机（SVM）

支持向量机（SVM）［12］由Vapnik等人提出，是一种基于模式识别发展而来的广义线性分类器。SVM的理论依据是统计学理论和结构风险最小化。SVM在小样本、非线性以及高维分类问题上表现优异，在解决分类器复杂性与泛化性之间的矛盾问题上比传统模式识别方法具有更大的优势，因此SVM被广泛应用于机器学习和模式识别领域并得到迅猛发展［12］。

2 基于K折交叉验证的SVM隧道围岩分级判别模型

建立隧道围岩级别与其判别指标之间的判别模型，利用K折交叉验证方法对样本进行分组，并通过SVM模型进行交叉训练，确定模型权重，构建基于K折交叉验证的SVM隧道围岩分级判别模型，其具体流程如图2所示。

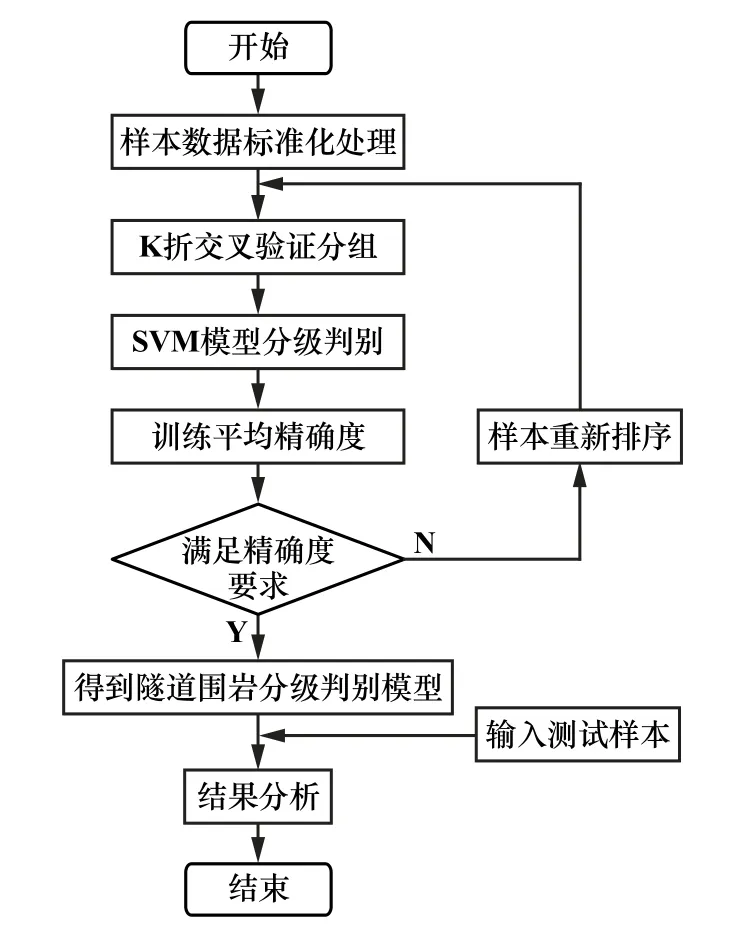
图2 模型实现流程

基于K折交叉验证的SVM模型的建立步骤如下：

1）整理和收集样本，并对数据进行标准化处理。

2）通过K折交叉验证方法对样本数据进行分组训练，选定K＝10。

3）将每个子集（4个样本）数据分别作为一次验证集，其余的9组子集（36个样本）数据作为训练集，这样会得到10次训练模型数据，带入到SVM模型中进行训练。

4）当模型平均准确率大于等于90%时认定该模型可以进行隧道围岩分级判别，并将训练模型最优结果权重确定为分类模型权重。若平均准确率小于90%，则将样本重新随机排序，返回到第2步再进行K折交叉验证。直至满足条件。

5）得到基于K折交叉验证的SVM隧道围岩的分级判别模型。

6）输入测试样本，得到分级判别结果。

3 模型应用与分析

3.1 指标体系构建与数据处理

收集了邓家湾隧道50组样本数据，如表1所示。根据TSP303系统确定判别指标为纵波速度X1（m／s）、横波速度X2（m／s）、纵横波速比X3、泊松比X4、密度X5（kg／m3）及静态杨氏模量X6（GPa），输出变量为判别等级Y，根据现场勘测得到样本隧道围岩包括2、3、4、5共4个等级。选取了40组样本对模型进行训练、10组样本进行测试。利用SPSS软件将样本数据标准化处理结果，如表1所示。

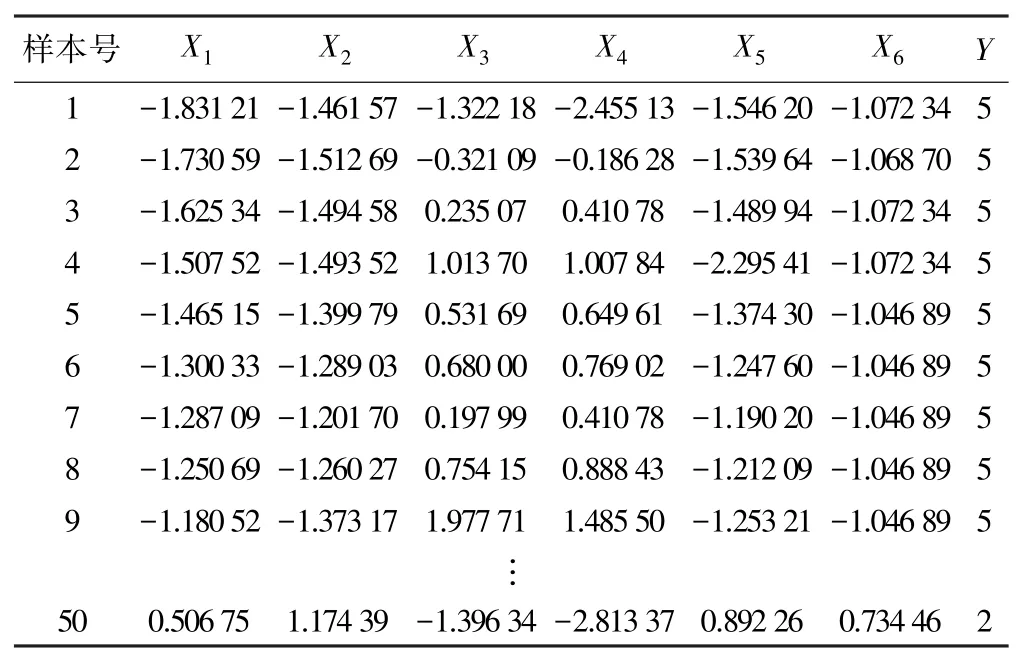
表1 标准化样本数据

3.2 模型的建立

采用Matlab2016（a）仿真平台建立隧道围岩分级判别模型，通过K折交叉验证方法对样本数据进行分组训练，选定K＝10，将每个子集数据分别作为一次验证集，其余9组子集数据组合起来作为训练集，带入到SVM模型中进行训练，针对多分类问题，SVM分类器选用fitcecoc函数。通过训练得到10组判别模型的准确率如图3所示，求得平均准确率为95%，证明该模型可以对隧道围岩进行分级判别，并确定分类模型的权重ω＝0.055 6。

图3 KCV⁃SVM判别模型准确率

3.3 判别结果对比分析

为了验证模型是否具有优良的泛化能力，通过输入10组测试样本数据进行预测，并分别与系统聚类分析方法、贝叶斯判别方法进行对比，结果如图4和表2所示。从图4可见，系统聚类分析和贝叶斯判别方法均有2个样本判别错误，而本文的KCV⁃SVM判别模型仅有1个样本判别错误。由表3可见，3种判别方法的准确率分别为80%、80%、90%，说明KCV⁃SVM模型判别准确率更高，更适用于隧道围岩的分级判别。

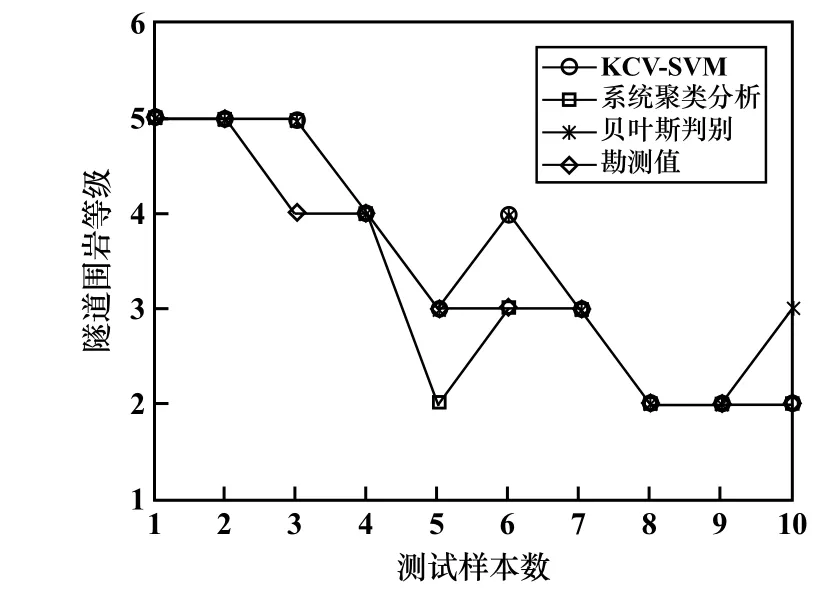
图4 不同方法的判别结果对比

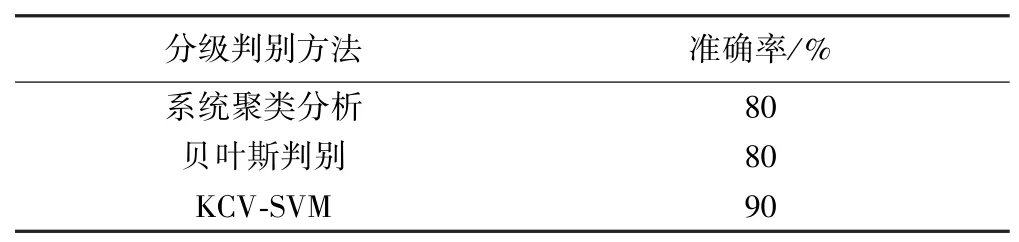
表2 3种方法准确率对比

4 结 论

1）建立支持向量机的隧道围岩分级判别模型，并采用K折交叉验证方法对样本进行分组，再代入到支持向量机模型进行交叉验证训练，可以更好地评估该模型的分级判别性能，在一定程度上减少过拟合现象；确定了分类模型的权重，避免了分类器靠经验值确定权重而导致精确度较低的现象。

2）采用K折交叉验证下的支持向量机模型对测试样本进行分级判别，仅1个样本判别错误，准确率达到90%；采用系统聚类分析和贝叶斯判别方法的准确率均为80%。通过对比得出：K折交叉验证下的支持向量机模型准确率更高，为隧道围岩的分级判别提供了新途径。