基于松动圈理论的隧道初期支护时机分析
2021-08-26王睿党发宁王靖媛邓祥辉袁岽洋
王睿 党发宁 王靖媛 邓祥辉 袁岽洋

摘要:
隧道开挖后,围岩应力将逐步释放,此时围岩变形增大、压力减小,若能有效确定隧道初期支护最佳施作时机,则既可充分发挥围岩自承能力减小支护结构强度,又可控制围岩变形,确保施工安全。以围岩拉应变达到岩体极限拉应变、围岩开始产生松动圈作为初期支护的最佳施作时机,建立了基于松动圈理论的隧道初期支护施作时机确定理论。运用Midas GTS有限元计算软件,分析各级围岩在应力释放全过程中围岩应力、应变、位移及松动圈的变化规律,确定Ⅲ级、Ⅳ级和Ⅴ级围岩在应力释放分别达到60%、40%和20%时是施作初期支护的最佳时机。
关 键 词:
围岩松动圈; 初期支护; 应力释放; 拉应变
中图法分类号: U451
文献标志码: A
DOI:10.16232/j.cnki.1001-4179.2021.07.024
0 引 言
隧道开挖后,围岩应力的释放存在明显的时间效应。而在围岩应力释放过程中,岩体损伤加剧、变形增大、围岩压力减小,支护结构所需提供的支护力也随之减小;若对围岩应力释放不加约束,将导致围岩变形过大、初支侵限甚至坍塌[1-3]。因此,确定隧道初期支护最佳施作时机,既可使围岩应力有效释放,减小支护结构强度,又可控制围岩变形,确保施工安全[4-5]。
1958年Lauffer提出了隧道围岩自稳时间的经验公式。从理论上讲,在围岩暂时稳定时间内施作初期支护均是可行的,但由于计算参数难以准确确定,使自稳时间可靠度较低,且自稳时间范围较大,无法确定初期支护最佳时机,常造成围岩过度松弛[6-7]。变形控制理论认为围岩应力释放最直观的表现就是位移的产生。根据围岩最大位移值、位移变化速率和位移速率变化趋势确定初期支护甚至二次衬砌的施作时机已在业界达成了广泛的一致[8-10],但现有的监控量测手段均是监测初期支护约束下支护结构和围岩的受力及变形情况,无法监测到隧道开挖后瞬时位移,对确定初期支护时机仅有参考作用[11]。李鹏飞等[12]通过分析含衬砌的深埋隧道在围岩应力释放过程中围岩应力的大小及变化规律,发现及时施作具有一定刚度的初期支护可以控制围岩应力的释放,减小围岩塑性变形,使围岩处于较好的三向受力状态,且当围岩最小主应力与最大主应力之间差值较小时,发生破坏的概率也会降低,故可通过建立应力释放系数与围岩应力的对应关系确定初期支护施作时机。文竞舟[13]模拟了圆形隧道Ⅳ级围岩应力释放系数为0.3,0.5,0.7时施作初期支护后,锚喷的力学性能和围岩塑性区状态,得到初期支护施作越晚,锚杆所受轴力越小、围岩塑性区半径越大的结论,说明此时围岩的变形已基本结束,锚喷支护作用已不明显,围岩容易引起松动和破坏,且Ⅳ级围岩应力释放系数为0.5时施作初期支护最佳。以上方法在理论上分析了初期支护施作时机和围岩自稳时间、围岩位移、围岩应力和支护结构受力之间的关系,但未给出评判标准和定量指标,因此对工程的指导意义有限[14-16]。
本文根据隧道围岩松动圈的产生及发展规律,提出新的初期支护施作时机理论,并运用数值模拟的方法,分析各级围岩隧道在应力释放过程中围岩位移、应力、拉应变和松动圈范围的变化规律,以期得到不同围岩级别隧道初期支护施作的最佳时机。
1 研究思路
松动圈是隧道开挖时围岩发生应力重分布,导致局部围岩拉应力超过岩体抗拉强度而产生受拉破坏而形成的。围岩松动圈的产生标志着岩体开始破坏,因此可把这一时刻作为施作初期支护的最佳时机,进而提出新的隧道初期支護施作时机确定理论。
通过分析隧道开挖后,在无支护条件下围岩应力释放过程中,即应力释放系数由0→0.1→0.2→0.4
→0.6→0.8→1.0变化的过程中,围岩位移、应力及拉应变的变化规律,以围岩的拉应变达到岩体极限拉应变开始(即将)产生破坏,并形成(即将形成)松动圈为判别标准,作为初期支护的最佳施作时机,建立基于松动圈理论的隧道初期支护施作时机理论。
具体方法如下:
(1) 建立隧道开挖后,初期支护尚未施作时,围岩应力释放系数分别为0.1,0.2,0.4,0.6,0.8,1.0的三维有限元数值计算模型。
(2) 分析不同应力释放系数下拱顶、拱肩、边墙、拱脚等关键节点围岩位移、应力、拉应变的变化规律以及松动圈的产生和发展规律,并绘制应力释放系数与围岩位移、应力、拉应变的关系曲线。
(3) 以围岩拉应变达到极限拉应变,同时开始(即将)产生松动圈为判别标准,所对应的应力释放系数即为初期支护施作时机。
2 数值分析
2.1 模型建立
2.1.1 工程概况
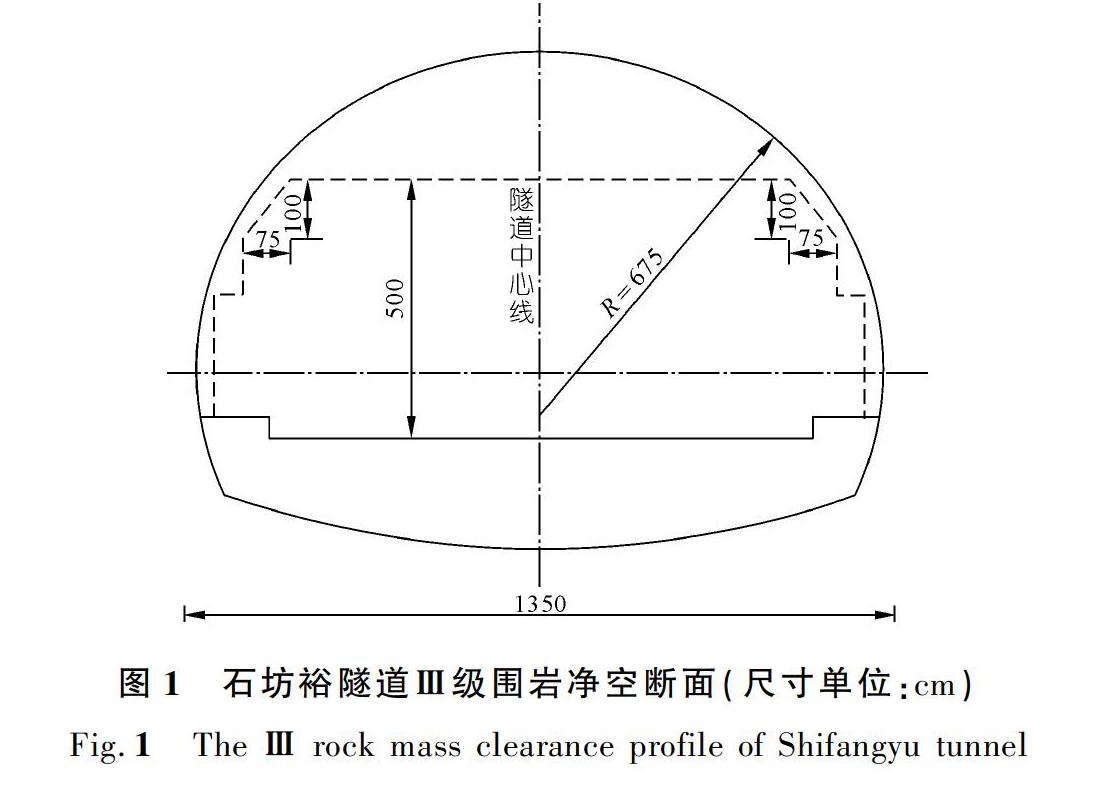
济南市二环南路快速路工程石坊裕隧道为分离式单向3车道长隧道,设计时速为80 km/h,建筑限界净宽13.5 m,净高5.0 m,采用内轮廓为R=6.75 m的单心圆设计,净空断面如图1所示。该隧道围岩为片麻岩,岩体较坚硬,进口段雨季时稳定性差,初期支护不及时易产生局部坍塌。侧压力系数Ⅲ、Ⅳ、Ⅴ级围岩分别取0.14,0.15,0.30,具体岩体物理力学参数由工程实测数据,并结合《工程地质手册》中参考值最终确定,详见表1所列。
2.1.2 模型尺寸及约束条件
采用Midas/GTS NX[17](Geotechnical and Tunnel Analysis System)数值分析软件进行模拟。数值计算时选取Ⅲ、Ⅳ、Ⅴ级围岩埋深为85 m的典型断面,建立Midas 3D模型,模型向左、向右、向下各取5倍的洞径,向上至自由面(埋深85 m),纵向取400 m,即宽×长×高为180 m×400 m×169 m。初始应力场按自重应力计算,水平向应力通过侧压力系数得到;假设模拟的材料为理想弹塑体,力学特性服从Hoek-Brown强度准则;模型底面施加XYZ方向的约束,上边界取自由面,侧面施加X方向的位移约束,隧道开挖方向施加Y方向位移约束。Ⅲ、Ⅳ、Ⅴ级围岩均采用全断面开挖,其中,Ⅲ级围岩不设仰拱、Ⅳ和Ⅴ级围岩仰拱在第二步开挖,各级围岩只研究第一步开挖时的应力释放,且仅模拟开挖一个进尺,各级围岩进尺分别为3.0,2.4,1.0 m。模型采用混合四面体划分网格,Ⅲ级围岩模型网格划分如图2所示,共19 099个单元,7 346个节点。
采用Midas软件自身所具有的功能,对自重应力状态下的围岩应力释放10%、20%、40%、60%、80%、100%时(即应力释放系数分别设置为0.1,0.2,0.4,0.6,0.8,1.0时)围岩关键点的位移、应力、拉应变及松动圈厚度进行分析计算。隧道横断面关键点提取位置为:拱顶(点1)、拱肩(点2、点3)、边墙(点4、点5)、拱脚(点6、点7)位置,共计7个,具体位置如图3所示。
其中,拱顶下沉取拱顶(点1)的竖向位移;围岩应力取岩体最大主应力;以岩体的极限拉应变作为判断松动圈厚度的标准。在工程现场采集各级围岩岩样,通过室内劈裂试验,测得Ⅲ级围岩的极限拉应变为155 με,Ⅳ级围岩的极限拉应变为135 με,Ⅴ级围岩的极限拉应变为115 με[18]。
2.2 Ⅲ级围岩计算结果
Ⅲ级围岩在不同应力释放系数下围岩应力和拉应变等值线图如图4~5所示,Ⅲ级围岩数值计算结果分析及围岩松动圈分布图如图6~7所示。
由图4~7可见:隧道开挖后Ⅲ级围岩随着应力释放,围岩压应力、拉应变、变形及松动圈呈以下趋势。
(1) 随着应力释放系数的增大,各关键点的圍岩应力趋势接近线性发展,关键点1~3(即拱顶及拱肩位置)的压应力不断减小,而关键点4~7(即边墙及拱脚位置)的压应力不断增大,且在横断面上由上至下围岩拉应力呈逐渐增大趋势。这是由于隧道开挖引起的围岩应力重分布使拱顶及拱肩部位的荷载逐步卸至边墙和拱脚。
(2) 随着应力释放系数的增加,各关键点的拉应变也随之增大,但从横断面上看分布并不均匀,拱顶(1点)应变最小,说明随着围岩应力的释放岩体的损伤持续增加,且不断向内部延伸。应力系数在0.8~1.0时,关键点6~7(即拱脚位置)上升速率明显加快。
(3) 随着应力的逐步释放,围岩拱顶下沉不断增大,拱顶沉降随应力释放系数的增加变化曲线接近斜率k=2.19的线性分布,表明岩体内部储存的能量可逐步转化为位移。
(4) 以岩体的极限拉应变值作为松动圈的判别依据。当应力释放系数达到0.8时,Ⅲ级围岩开始产生松动圈,且松动圈厚度随着应力释放系数的增加不断增加。沿隧道横断面,松动圈呈拱顶大、向边墙逐步减小的趋势,当应力释放系数为1.0时,拱顶的松动圈厚度达到2.70 m。
(5) 应力释放系数为0.6时,虽未产生松动圈,但关键点6的拉应变达到154.9 με。此时岩体的拉应变已非常接近Ⅲ级围岩的极限拉应变155.0 με,因此Ⅲ级围岩在应力释放到60%时是施作初期支护的最佳时机。
2.3 Ⅳ级围岩计算结果
Ⅳ级围岩数值模拟结果统计及围岩松动圈分布图如图8~9所示。
从图8~9可见:隧道开挖后当应力释放系数达到0.6时Ⅳ级围岩开始产生松动圈,且松动圈厚度随着应力释放系数的增加不断增加;但应力释放系数为0.4时,虽未产生松动圈,但关键点6的拉应变已达到131.8 με,已非常接近Ⅳ级围岩的极限拉应变135.0 με,因此Ⅳ级围岩在应力释放到40%时是施作初期支护的最佳时机。
2.4 Ⅴ级围岩计算结果
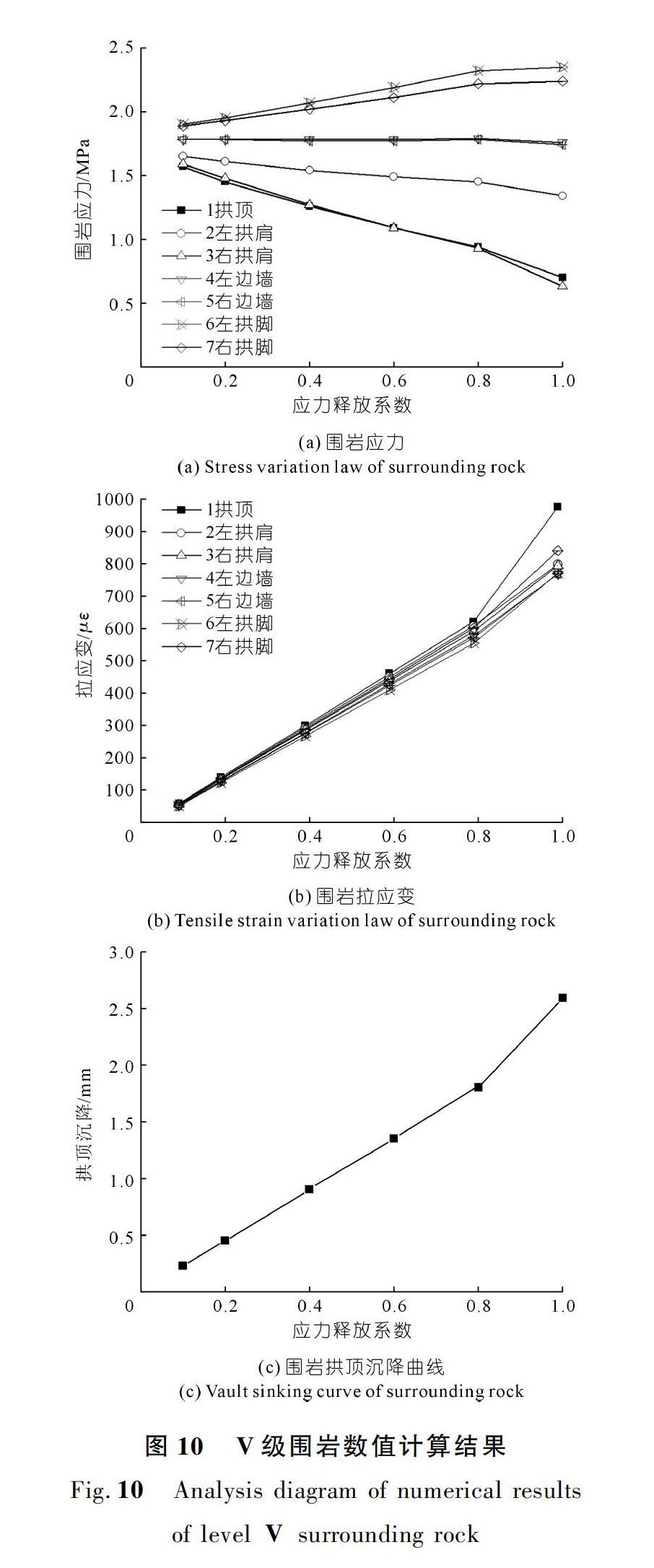
Ⅴ级围岩在不同应力释放系数下应力、拉应变、拱顶下沉、围岩松动圈的变化趋势如图10~11所示。
从图10~11可见:隧道开挖后应力释放系数达到0.2时Ⅴ级围岩开始产生松动圈,且松动圈厚度随着应力释放系数的增加不断增加,沿隧道横断面松动圈呈拱顶大、向边墙逐步减小的趋势。因此Ⅴ级围岩在应力释放到20%时施作初期支护最佳。
3 结 论
本文在分析现有隧道初期支护施作时机确定方法不足的基础上,提出了基于松动圈理论的隧道初期支护时机确定方法,并采用数值模拟得到了Ⅲ级、Ⅳ级和Ⅴ级围岩初期支护最佳施作时机,具体结论如下。
(1) 以围岩拉应变达到岩体极限拉应变,围岩开始产生松动圈为判别标准,作为初期支护的最佳施作时机,建立了基于松动圈理论的隧道初期支护施作时机确定理论。
(2) 运用Midas GTS数值计算软件分别计算了Ⅲ级、Ⅳ级和Ⅴ级围岩应力释放10%、20%、40%、60%、80%、100%时,围岩关键点的位移、应力、拉应变及松动圈厚度变化规律。随着应力释放系数的增大,围岩拱顶下沉值不断增加,拉应变不断增加;而拱部压应力逐渐减小,边墙部位变为递增趋势。
(3) 根据隧道围岩松动圈的产生及发展规律,确定Ⅲ级、Ⅳ级和Ⅴ级围岩在应力释放分别到60%、40%和20%时是施作初期支护的最佳时机。由于拱顶下沉值与应力释放系数成比例,故在工程施工中通过实时监测拱顶下沉变化,当Ⅲ级、Ⅳ级和Ⅴ级围岩拱顶下沉分别达到最终变形量的60%、40%和20%时即为应力释放分别达到60%、40%和20%的时刻,是施作初期支护的最佳时机。
参考文献:
[1] 张顶立.隧道及地下工程的基本问题及其研究进展[J].力学学报,2017,49(1):1-19.
[2] 刘乃飞,李宁,郭晓刚,等.软弱围岩隧洞位移和应力释放规律研究[J].地下空间与工程学报,2017,13(3):643-650.
[3] 仇文革,孙克国,王立川,等.基于围岩稳定性的大断面隧道初期支护优化[J].土木工程学报,2017,50(增2):8-13.
[4] 刘招伟,王明胜,方俊波.高地应力大变形隧道支护系统的试验研究[J].土木工程学报,2010,43(5):111-116.
[5] 李贤,蔡林真.某软岩隧道变形规律和二衬最佳支护时机选择研究[J].中外公路,2019,39(3):189-192.
[6] LI P,ZHANG Z,TAO L.Stability ranking system of rockmass surrounding a large-scale underground cavern group[J].Journal of Engineering Geology,2004,12(1):25-29.
[7] NGUYEN V M,NGUYEN Q P.Analytical solution forestimat-ing the stand-up time of the rock mass surrounding tunnel[J].Tunnelling and Underground Space Technology,2015,47:10-15.
[8] 龔晓南,杨仲轩.岩土工程变形控制设计理论与实践[J].岩土力学,2018,39(增2):273.
[9] LUNARDI P.隧道设计与施工:岩土控制变形分析法[M].北京:中国铁道出版社,2011.
[10] 陈鹤,乔春生.富水黄土隧道初期支护监控及分析[J].西部探矿工程,2003,15(1):105-106.
[11] 周烨,李鹏飞,张翾.大断面黄土隧道初期支护合理施作时机[J].北京交通大学学报,2012,36(1):41-47.
[12] 李鹏飞,赵勇,张顶立,等.考虑应力释放含衬砌的深埋圆形隧道应力及变形的弹塑性解[J].中国铁道科学,2013,34(2):58-65.
[13] 文竞舟.隧道初期支护力学分析及参数优化研究[D].重庆:重庆大学,2012.
[14] 周烨.高速铁路黄土隧道初期支护受力特性研究[J].现代隧道技术,2012,49(3):83-86,93.
[15] 胡卫军,程桦,荣传新,等.深井软岩大断面硐室合理支护时机分析[J].煤矿安全,2015,46(5):186-189.
[16] XU J C,NI Y D.Displacement ratio dichotomy back analysis of surrounding rock-primary support system of weathered rock tunnel[J].Arabian Journal of Geosciences,2019,12(6):18-29.
[17] 夏峰.地下硐室围岩松动圈影响因素分析[D].哈尔滨:中国地震局工程力学研究所,2009.
[18] 冯学敏,陈胜宏,李文纲.岩石高边坡开挖卸荷松弛准则研究与工程应用[J].岩土力学,2009,30(增2):452-456.
(编辑:郑 毅)
引用本文:
王睿,党发宁,王靖媛,等.基于松动圈理论的隧道初期支护时机分析
[J].人民长江,2021,52(7):141-147.
Analysis on primary support timing of tunnel based on loose circle theory
WANG Rui1,DANG Faning2,WANG Jingyuan1,DENG Xianghui1,YUAN Dongyang3
(1.School of Civil and Architecture Engineering,Xi′an Technological University,Xi′an 710021,China; 2.School of Civil Engineering and Architecture,Xi′an University of Technology,Xi′an 710048,China; 3.Zhejiang Scientific Research Institute of Transport,Hangzhou 310023,China)
Abstract:
After tunnel excavation,the surrounding rock stress will be released gradually,accompanied with increase of surrounding rock deformation and decrease of pressure.At this time,if the optimal timing of the primary support of the tunnel can be effectively determined,the self-supporting capacity of the surrounding rock can be put into full play to reduce requirement on strength of supporting structure and to control the rock deformation,ensuring the construction safety.Taking the criterion that the tensile strain of surrounding rock reaches the ultimate tensile strain and the rock mass begins to generate loose circle as the optimal timing of the primary support,we established a theory of determining the timing of the primary support based on the loose circle theory.Meanwhile,the change rules of stress,strain,displacement and loose circle of the surrounding rock in process of stress release were analyzed by using Midas GTS finite element software.Based on the loose circle theory,it is determined that the optimal timing of primary support is stress release reaching 60%,40% and 20% for the surrounding rock of grade III,IV and V respectively.
Key words:
loose circle of rock mass;primary support;stress release;tensile strain
