HPM视角下的“二面角”概念教学设计与实践

高振严 韩嘉业

【摘 要】文章重构式地运用数学史料，引导学生从实际情境中抽象出二面角的概念，并设置一系列探究活动，让学生思考并讨论二面角的平面角定义的合理性。在这一过程中，培养学生的数学抽象和逻辑推理的核心素养。数学史为该节课预测学生学情、设置探究问题、解释定义合理性提供了素材和思路，同时也为学生树立正确的数学观提供了德育路径。

【关键词】二面角;二面角的平面角;数学史;教学实践

【作者简介】高振严，一级教师，宝山区教学能手，宝山区教育系统十佳青年，主要研究方向为数学史与数学教育;韩嘉业，高中数学教师，主要研究方向为数学史与数学教育。

【基金项目】上海高校“立德树人”人文社会科学重点研究基地之数学教育教学研究基地研究项目——数学课程与教学中落实立德树人根本任务的研究（A8）

一、引言

“二面角”是沪教版高中数学教材第14章“空间直线与平面”的第4节“空间平面与平面的位置关系”的第一节课，是继空间内异面直线所成的角、直线与平面所成的角之后的又一个空间角。教材在引入二面角的概念之后，直接构造二面角的平面角，然后证明二面角的平面角的唯一性，即二面角的平面角的大小不随顶点位置的变化而变化。遗憾的是，教材并没有探讨二面角的平面角定义的合理性，即为什么可以用二面角的平面角的大小来度量二面角的大小。

历史上，法国数学家勒让德（A.M.Legendre）曾经论证过二面角的平面角定义的合理性，但勒让德的论证对高中学生来说并不易理解。基于以上原因，本节课从帮助学生构建数学理解的角度，设计二面角的数学探究活动，以及用蛋糕块模拟二面角的直观模型，从定性和定量两个方面让学生理解二面角的平面角定义的合理性。本节课的重点是二面角和二面角的平面角概念，难点是二面角的平面角概念的形成过程。具体的教学目标如下。

（1）观察现实生活的情境，抽象出二面角的概念，培养数学抽象素养。

（2）探究二面角的平面角的定义，发展学生的逻辑推理素养。

（3）感悟数学概念所蕴含的理性精神。

二、数学史料及应用

为了更好地帮助学生构建对二面角概念的理解，并向学生解释二面角的平面角定义的合理性，本节课需用到以下数学史料。

（一）二面角概念的形成

古希腊数学家欧几里得在其《几何原本》第11卷中给出面面倾角的定义：从两个相交平面交线上的同一点，分别在两平面内各作交线的垂线，这两条垂线所夹的锐角叫作该两平面的倾角（或称交角）[1]。欧几里得并没有提出二面角的概念，他考虑的仅仅是两个平面之间的一种关系。这也是在课堂上的学生最容易出现的对二面角概念的错误理解。以史为鉴，教师应向学生解释，二面角与面面夹角之间是有区别的。

1829年，美国数学家沃克（T.Walker）在其《几何基础》中，提出了平面角（plane angle）的概念[2]。但沃克对二面角的认识还是模糊的，仍然聚焦于两个平面夹角的度量。二面角及其棱和面的概念以及二面角的记号等都付之阙如。这一历史素材表明，人们对二面角概念的认识是从具体到抽象的过程，所以在教学中也应该遵循这一原则。

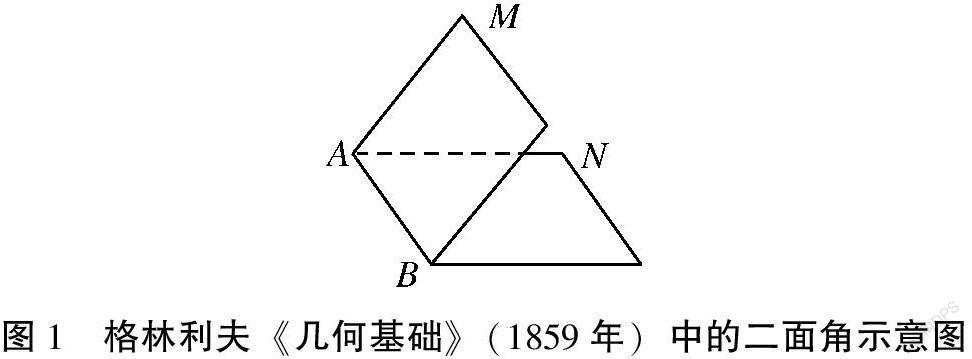
1859年，美国数学家格林利夫（B.Greenleaf）在其《几何基础》中指出，二面角是由两个相交平面所形成的角，并给出示意图（如图1）。编者虽未指明“半平面”，但其示意图显示的是两个半平面所形成的角[3]。书中提出了一些新的名称，如二面角（dihedral angle）、二面角的面（face）、二面角的棱（edge），还给出了二面角的字母表示法。至此，二面角作为几何图形的概念登上了数学历史舞台。但可以预见的是，学生在学习二面角的概念时，可能会忽视定义中的“半平面”。

1922年，美国数学家赛克斯（M.Sykes）和康斯托克（C.E.Comstock）在他们合著的《立体几何》中给出二面角的定义：“两个具有公共边界的半平面所形成的图形称为二面角。”[4]21-31同時，书中给出面和棱的概念，以及二面角的命名方式，与现行教科书一致。

（二）二面角的平面角概念

关于二面角的测量，赛克斯和康斯托克在《立体几何》中提出了“平面角”的概念：从两个平面的交线上任取一点，过该点分别在两个平面内作交线的垂线，垂线形成的夹角称为平面角。书中给出了以下两个定理。[4]21-31

定理1：一个二面角的所有平面角都相等。

定理2：如果一个平面垂直于二面角的棱，它与两个面的交线形成平面角。

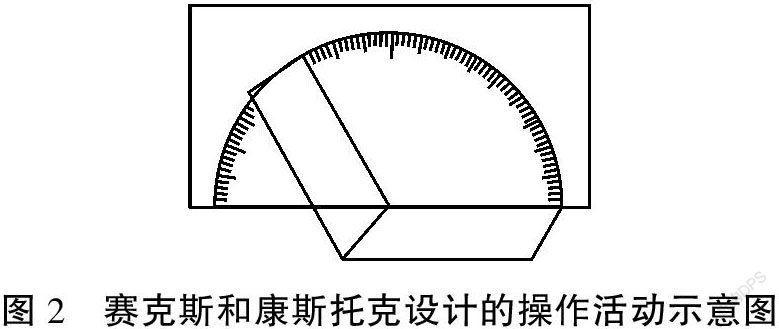
另外，编者还设计了一个操作活动：通过剪切、折叠卡纸来制作一个二面角，并展示测量该二面角大小的过程（如图2）。这一活动可以让学生直观地感受二面角的图形概念，并启发学生思考如何用符合直觉的、合理的方式来度量二面角的大小。

（三）二面角平面角合理性之定量研究

勒让德在《几何基础》（1794年）中提出，为了说明二面角的平面角定义的合理性，需要证明若二面角以一定的比例增大或减小，则相应的平面角将以相同的比例增大或减小[5]。因此，若两个二面角的平面角是可公度的，则它们所对应的二面角具有相同的比例。勒让德将证明从平面角可公度的情形扩展到了平面角不可公度的情形。现行教科书常利用极限的方法来达成这一扩展。勒让德的证明方法涉及可公度的概念，不易为高中生所理解，但教师可以让学生通过观察实物来直观感受二面角与它的平面角对应成比例的结论，由此理解二面角的平面角定义的合理性。

（四）二面角的平面角合理性之定性研究

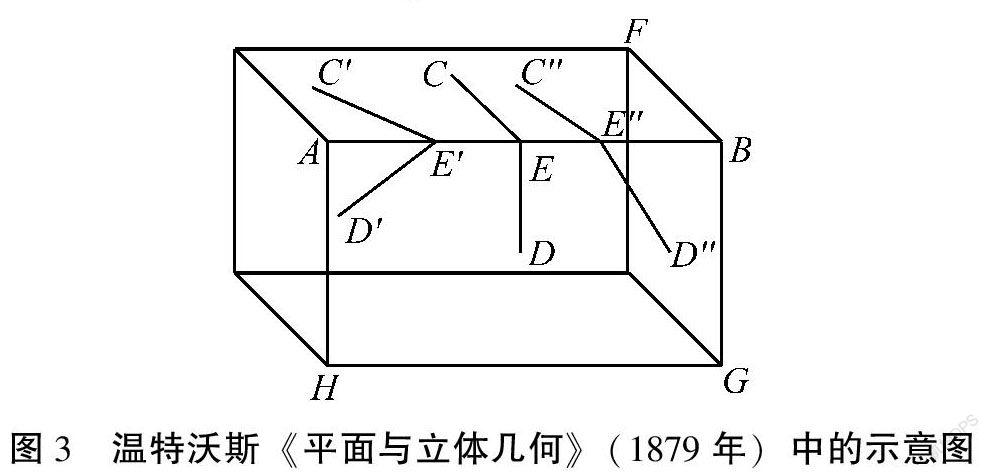
1879年，美国数学家温特沃斯（G.A.Wentworth）在其《平面与立体几何基础》中讨论了“平面角的边必须垂直于棱”的缘由。如图3，在长方体中，二面角F-AB-H是一个直二面角，∠CED的两条边分别在平面AF和平面AG上，并且它们都垂直于直线AB，所以∠CED是二面角F-AB-H的平面角。值得注意的是，图中另外画出的两个角，它们的两条边均不垂直于直线AB，通过观察可知，∠C′E′D′是锐角，∠C″E″D″是钝角，都不能合理地刻画直二面角F-AB-H。这样的定性说明，对于高中生来说较易于理解。

三、教学设計与实施

（一）情境引入

教师借助生活中的三个情境：翻开的书页、墙面与天花板、打开的笔记本电脑，引入二面角。

师：借助上述生活中的情境，大家可以抽象出什么数学问题？

生：两个平面的夹角。

师：两个平面的夹角的概念最早由古希腊数学家欧几里得在《几何原本》中给出。

（教师在PPT上展示两平面夹角的概念。）

师：两平面所成的对顶角有两对，选哪一对作为它们的夹角？

生：较小的一对。

师：那么，两平面夹角的范围应该是多少？

（学生陷入沉思中。）

师：如果我们给出一个新的概念：平面上的一条直线将平面分成两个半平面。我们怎样用数学语言描述刚才的情形？

生：两个半平面所成的图形。

师：还有补充吗？

生：两个半平面及其交线所组成的空间图形。

师：所以我们将由两个半平面α和β及其交线AB所组成的空间图形称为二面角，记作α-AB-β。两个半平面α和β称为二面角的面，交线AB称为二面角的棱。下面请同学们画出开合程度较小和较大的两种情形的二面角。

【设计意图】从学生熟悉的生活情境入手，学生较容易抽象出两个平面的夹角这一数学模型，这与欧几里得的想法有相似之处。但是，通过分析前面的生活情境，发现这一模型不能表示开合程度较大的笔记本电脑，所以需要引入一个不同于两平面夹角的新概念，即二面角。在这一过程中，学生注意到二面角的定义中“半平面”的重要性。

（二）探究发现

本教学环节设置了三个探究活动：（1）通过测量折纸所形成的二面角的大小，引出研究平面角的必要性;（2）通过三种特殊的二面角（0°、90°、180°）与其对应的平面角大小的比较探究，定性分析二面角的平面角定义的合理性;（3）通过从内部测量二面角大小的活动，自然地引出二面角的平面角的唯一性问题，并加以证明。

【探究活动1】

师：请大家用手中的A4纸折出一个二面角，并用量角器测量它的大小。

（学生所折的二面角分成了两类：一类是将A4纸对折，纸的边缘与折痕垂直;另一类是斜折，纸的边缘与折痕不垂直。）

师：大家是怎样折二面角的？又是如何测量的？

生1：我将A4纸对折（如图4），然后将量角器紧贴二面角边缘的两边测量。

师：还有不同的折法吗？

生2：我将A4纸斜折（如图5），然后也是将量角器紧贴二面角边缘的两边测量。

师：我看到有的同学也是斜折，但测量方法不同。

生3：我也是将A4纸斜折，但我觉得测量边缘不方便，所以我把纸再次折叠，这次是对折，使之与上一次的折痕重叠，此时新的折痕垂直于原来的折痕（如图6），测量新折痕的夹角即可。

师：大家的做法非常好，二面角是一个空间图形，这几位同学测量的是一个平面角还是空间角？

生（齐答）：平面角。

师：为什么是平面角？

生4：大家所量的角都是纸的边缘或折痕的夹角，是两条交于一点的射线所成的角，符合平面角的定义。

师：前几节课，我们在度量异面直线所成的角、线面角等空间角时，都是把空间角转化成平面角进行度量，那么二面角也不例外。

【设计意图】度量是测量在数学中的抽象，测量是度量在现实世界的应用。本教学环节通过让学生动手测量二面角的大小，引导学生思考并发现测量的角其实是平面角而非空间角，从而得出立体几何中空间角度量的本质是平面角的度量，让学生体会到引入二面角的平面角的必要性。

【探究活动2】

师：刚刚三位同学选择的平面角有何不同？

生5：同学1和同学3选的平面角的两边都垂直于二面角的棱，同学2选的平面角的两边与棱不垂直。

师：你观察得很仔细。大家觉得应该选择哪一种平面角来度量二面角呢？

（大部分学生选择垂直的情况，也有一部分学生觉得垂直、倾斜都可以，还有极少数学生选择倾斜的情况。）

师：大部分同学的选择与历史上数学家欧几里得的选择相同，他就是用这种垂直于棱的平面角来度量两个平面所成角的大小。但是为什么欧几里得选择了垂直的情况，舍弃了倾斜的情况？理由是什么？

生6：如果是倾斜的情况，二面角的两个半平面重合时，两条倾斜的边并不重合（如图7）。

生7：不对，在这种情况下，两条倾斜的边可以重合，例如两边与棱的夹角都是30°。

生6：那在这种情况下，将二面角摊平，两个半平面在同一平面上，二面角是平角，此时两条倾斜的边并不在同一条直线上（如图8）。

师：两位同学举的反例都非常好。现在我们知道，如果平面角的两边不与二面角的棱垂直，那么平面角就不能正确地表示二面角的开合程度。

生8：有没有这种可能，倾斜的情况只是不能表示两个半平面重合以及摊平的情况，但是其他情况是可行的？

生9：不对，倾斜的情况也不能正确地表示两个半平面相互垂直的情况。

（该学生通过测量两个半平面相互垂直时，两种倾斜程度不同的平面角的大小，一种情况大于90°，另一种情况小于90°。这与历史上美国数学家温特沃斯的例证有异曲同工之妙。）

师：综上可知，倾斜的平面角不能正确地反映二面角的开合程度。那么垂直的平面角能正确地反映二面角的开合程度吗？

生10：可以，我可以用对折的纸来演示说明。

（学生用对折的纸演示平面角垂直于棱的情况。当两个半平面重合时，平面角的两边重合;当两个半平面垂直时，平面角的两边垂直;当两个半平面共面时，平面角的两边共线。）

师：通过刚才的演示可見，平面角的两边均垂直于棱时，它的开合程度与二面角一致。因此，我们选择两边均垂直于棱的平面角来度量二面角。

【设计意图】通过问题串引发学生对二面角的平面角定义合理性的思考。学生在交流环节相互质疑、相互启发，从而引发进一步深入的思考。最后，通过生生交流、师生交流的若干次循环，学生定性地得到了二面角的平面角的定义合理性。在这一环节中，学生逐步体会到一个良好的数学定义不是凭空产生的。

【探究活动3】

师：刚才大家所演示的平面角都位于折纸的边缘，然而我看到有的同学构造了位于折纸的内部的平面角。

（学生演示将直角三角板置于折纸内部来构造直二面角的情形。）

师：平面角有时在边缘，有时在内部，随着位置的变化，它的大小会发生变化吗？

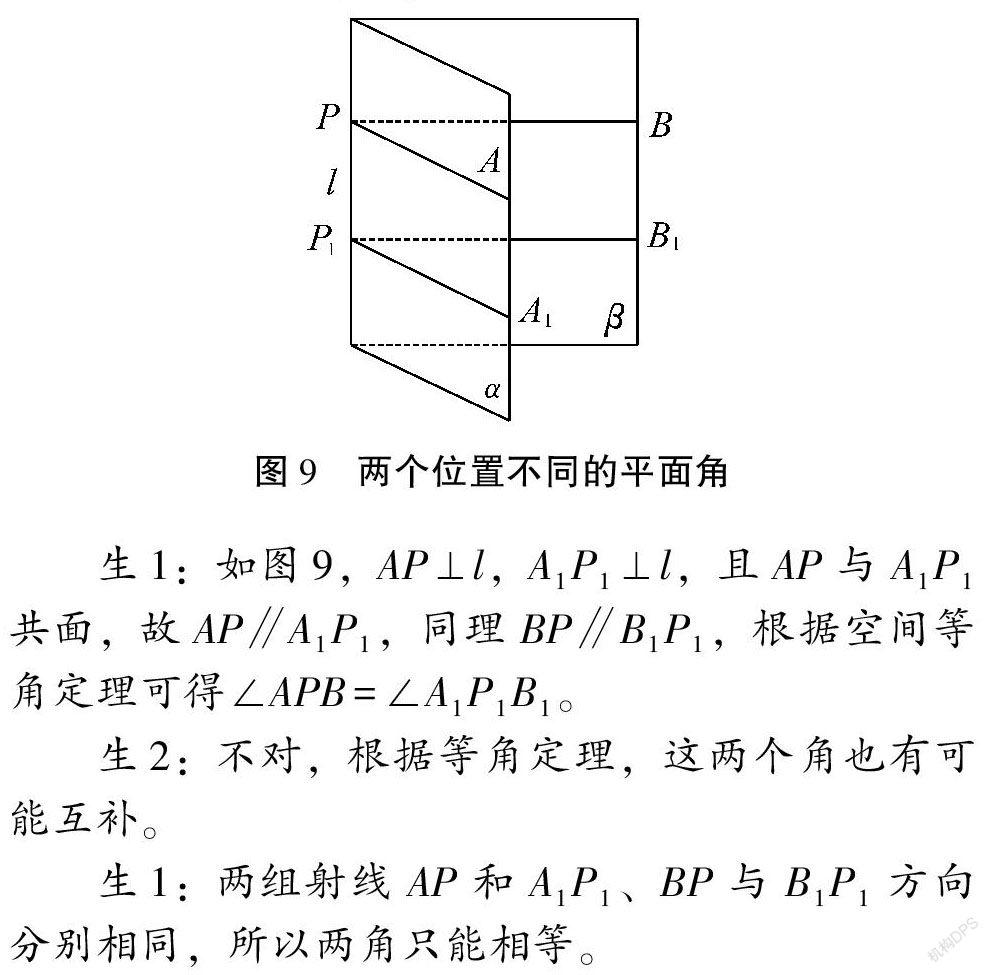
（教师在PPT上展示两个位置不同的平面角。）

生1：不会发生变化。

师：理由是什么？

生1：如图9，AP⊥l，A1P1⊥l，且AP与A1P1共面，故AP∥A1P1，同理BP∥B1P1，根据空间等角定理可得∠APB=∠A1P1B1。

生2：不对，根据等角定理，这两个角也有可能互补。

生1：两组射线AP和A1P1、BP与B1P1方向分别相同，所以两角只能相等。

师：由此可见，二面角的平面角的大小和它的顶点在棱上的位置无关。请大家总结一下二面角的平面角的定义。

生3：在二面角的棱上任取一点，过该点在两个半平面内分别作棱的垂线，所得平面角即为二面角的平面角。

（教师在PPT上展示二面角的平面角的概念，学生修正自己提出的概念。）

【设计意图】如何自然地引入二面角的平面角的唯一性证明，这是教学中的一个难题。在本节课的折纸活动中，当折纸的边缘与折痕不垂直时，有些学生感到无法测量二面角，但学生想到了将三角板内移，让折痕垂直于三角板，从而构造45°或90°的二面角。这样就自然地产生了在二面角的棱上选取位置不同的平面角顶点时，平面角是否相等的问题，从而顺利地引入平面角唯一性的证明。

（三）深化理解

通过几个特殊情况的折纸活动，说明了平面角为什么不采用倾斜的情况来定义，初步让学生认识到垂直情形的合理性。上述教学环节是对平面角定义的合理性的定性探究，本教学环节继续深入研究，对平面角定义的合理性进行定量分析。

师：刚才我们通过三种特殊的二面角，初步体会了平面角定义的合理性，但是还不够严密。数学史上有严格的证明来论证二面角平面角定义的合理性，但由于证明比较复杂，我们仅用实物来演示证明过程中一种情况：可公度的情况。

教师拿出三块大小一样的楔形蛋糕，向学生展示一块蛋糕的两个侧面构成了一个二面角，而蛋糕上沿的两条棱构成了该二面角的平面角。教师拿出两块蛋糕拼在一起，此时两块蛋糕的不重合的两个侧面构成了一个新的二面角，相应地，蛋糕上沿两条不重合的棱构成了新的二面角的平面角。

师：新二面角是原二面角的几倍？

生：两倍。

师：新二面角的平面角是原二面角的平面角的几倍？

生：两倍。

师：我再拿一块蛋糕拼在一起，现在二面角与平面角分别是原来的几倍？

生：三倍。

师：由此我们可以得出什么结论？

生：二面角大小的变化与平面角大小的变化是同比例的。

师：当平面角为0°时，二面角的两个半平面重合;当平面角为90°时，二面角的两个半平面垂直;当平面角为180°时，二面角的两个半平面也是平的。又因为二面角大小的变化与平面角大小的变化是同比例的，所以我们可以用二面角的平面角来度量二面角的大小。当平面角为n°时，二面角的大小也为n°，所以二面角的范围是0°≤n°≤180°。

【设计意图】数学史上对二面角的平面角定义的合理性的定量证明，分为可公度情形和不可公度情形两种情况。因为高中生没有接触过公度的概念，所以具体证明过程对他们来说并不易理解。但是，蛋糕模型作为可公度情形的一个简单、直观的例子，可以让学生从定量的角度来理解平面角与二面角大小变化的同比例关系。

（四）例题应用

在本教学环节，教师用两道典型例题（等腰型的二面角、全等型的二面角），让学生掌握二面角的平面角的作图方法，以及如何计算二面角的大小。例题讲解过程略。根据单元教学设计的规划，更多的应用问题将会在下一课时中讲解。

（五）课堂小结

师：本节课大家有什么收获？

生1：学习了二面角的概念以及两种典型二面角的平面角的作图方法。

师：这位同学谈到了在知识和方法上的收获，那么大家在数学思想上有何收获？

生2：学到了化归思想。

生3：体会到了学习立体几何时，实践操作的重要性，以及给出数学定义的时候需要考虑严谨性、合理性。

生4：数学的发展不是一蹴而就的，数学家也会犯错误、走弯路，但是数学家们的不懈努力创造了现在的数学成就。

师：大家总结得非常好。我再补充一点，立体几何的概念大都是从现实生活中抽象出来的，因此我们也要重视数学抽象的重要性。

【设计意图】在教师的引导下，学生从知识、方法、数学思想三个层面总结本节课的收获，充分挖掘本节课的教育价值[6]。

四、结语

课后问卷调查显示，97.8%的学生认为这节课中数学史内容对学习有帮助，93.3%的学生能正确掌握二面角、二面角的平面角的定义;88.9%的学生能够正确地作出给定二面角的平面角;84.4%的学生能够解释二面角的平面角定义的合理性，包括从不变性、等比例变化等角度来解释。本节课的亮点和价值笔者用五个“一”来概括。

（1）一个预测的窗口。欧几里得曾经给出了不完善的二面角定义，这也是学生在理解二面角概念过程中的一个常见错误。数学史上的谬误，为教师预测学生学情和潜在的学习困难打开了一扇窗户。

（2）一条有效的路径。数学史料中对于二面角的平面角的定义合理性的论述，作为教材的补充材料，为学生发展逻辑推理的核心素养提供了一条有效的路径。学生通过这堂课的学习，初步接触了如何讨论数学定义的合理性问题。

（3）一个探究的机会。为了有效落实“把课堂还给学生”的教学理念，本节课为学生提供了丰富的探究机会，而探究的问题则取材于历史的素材，由学生在前序的探究过程中自然地提出新的探究问题。

（4）一次突破的尝试。融入数学史的二面角概念教学并不常见，而在概念教学中加入关于二面角的平面角定义合理性的探究，是一次突破性的尝试。这对于数学基础较好的学生来说，是基于学情的一次合理突破，也是提升学生能力的一次有效尝试。

（5）一节难忘的课堂。从课后学生的反馈来看，学生对数学史的内容以及直观的蛋糕模型都具有深刻的印象，这说明本节课精心设计的亮点得到了学生的肯定，而这些亮点将会逐步改变数学课在学生心中枯燥乏味的印象。

参考文献：

[1]欧几里得.几何原本[M].兰纪正，朱恩宽，译.西安：陕西科学技术出版社，2003.

[2]WALKER T.Elements of geometry[M].Boston：Richardson & Lord，1829.

[3]GREENLEAF B.Elements of geometry[M].Boston：Robert S.Davis & Company，1859.

[4]SYKES M，COMSTOCK C E.Solid geometry[M].Chicago：Rank Mcnally & Company，1922.

[5]LEGENDRE A M.Elements of geometry[M].Cambridge，N.E.：The University Press，1794.

[6]余慶纯，汪晓勤.基于数学史的数学文化课例研究[J].中小学课堂教学研究，2021（1）：5-9.

（责任编辑：陆顺演）