谐波传动系统齿廓优化设计与侧隙控制补偿

2021-12-17李武超陈定方张慧明吴俊峰

武汉科技大学学报 2021年1期

李武超，梅杰，陈鹏,，郭政，陈定方，张慧明，吴俊峰

(1.武汉理工大学物流工程学院，湖北武汉，430063；2.湖北科峰智能传动股份有限公司，湖北黄冈，438000)

谐波减速器具有轻量化、传动比高等优点，在医疗器械、航空航天、机器人等精密传动领域被广泛应用。我国对谐波减速器的研究起步较晚，虽然近几年国内企业经过经验积累和技术沉淀，已经逐步获得国际市场认可，但是国内企业生产的谐波减速器在传动精度、传动效率、平均寿命等方面与国外企业仍有一定差距，目前我国在精密减速机领域主要依赖进口[1]。

谐波减速器的柔轮在运动时会发生空间变形，将其视为刚体进行设计得到的刚轮齿廓在传动过程中会产生啮合干涉或啮合不足等情况，同时，考虑到实际工作中齿侧间隙存在的必要性，为了能够兼顾传动精度以及润滑散热的需要，有必要对刚轮齿廓进行进一步优化。目前关于齿侧间隙的计算大多是建立在对共轭齿廓的形状及其相对位置研究的基础上，研究的重点主要是通过改进计算方法从而提高结果的精度方面[2]。为此，本文基于ANSYS有限元仿真数据,采用包络法对谐波减速器的刚、柔轮共轭齿廓进行设计和初步优化;在对刚轮空间齿廓进一步优化时,在刚轮与柔轮齿廓之间设定一个齿侧间隙常数，建立谐波传动系统的动力学模型，采用PID控制补偿方法对谐波传动系统的齿侧间隙误差控制补偿进行研究，以期为谐波传动系统综合性能的提高提供参考。

1 谐波传动共轭齿廓设计

1.1 谐波传动平面几何运动学分析

在不影响谐波传动性能的情况下，对谐波齿轮啮合系统进行简化处理，做出如下平面运动学假设[3]：(1)柔轮中线形状与波发生器一致，且周长始终不变；(2)波发生器在运动时始终不产生变形；(3)柔轮和刚轮的轮齿形状始终不变；(4)柔轮中线和特征圆始终保持等距关系。

本文将波发生器简化为余弦凸轮，在波发生器塞入柔轮之后，柔轮的中性层曲线变化情况如图1中的实线所示。

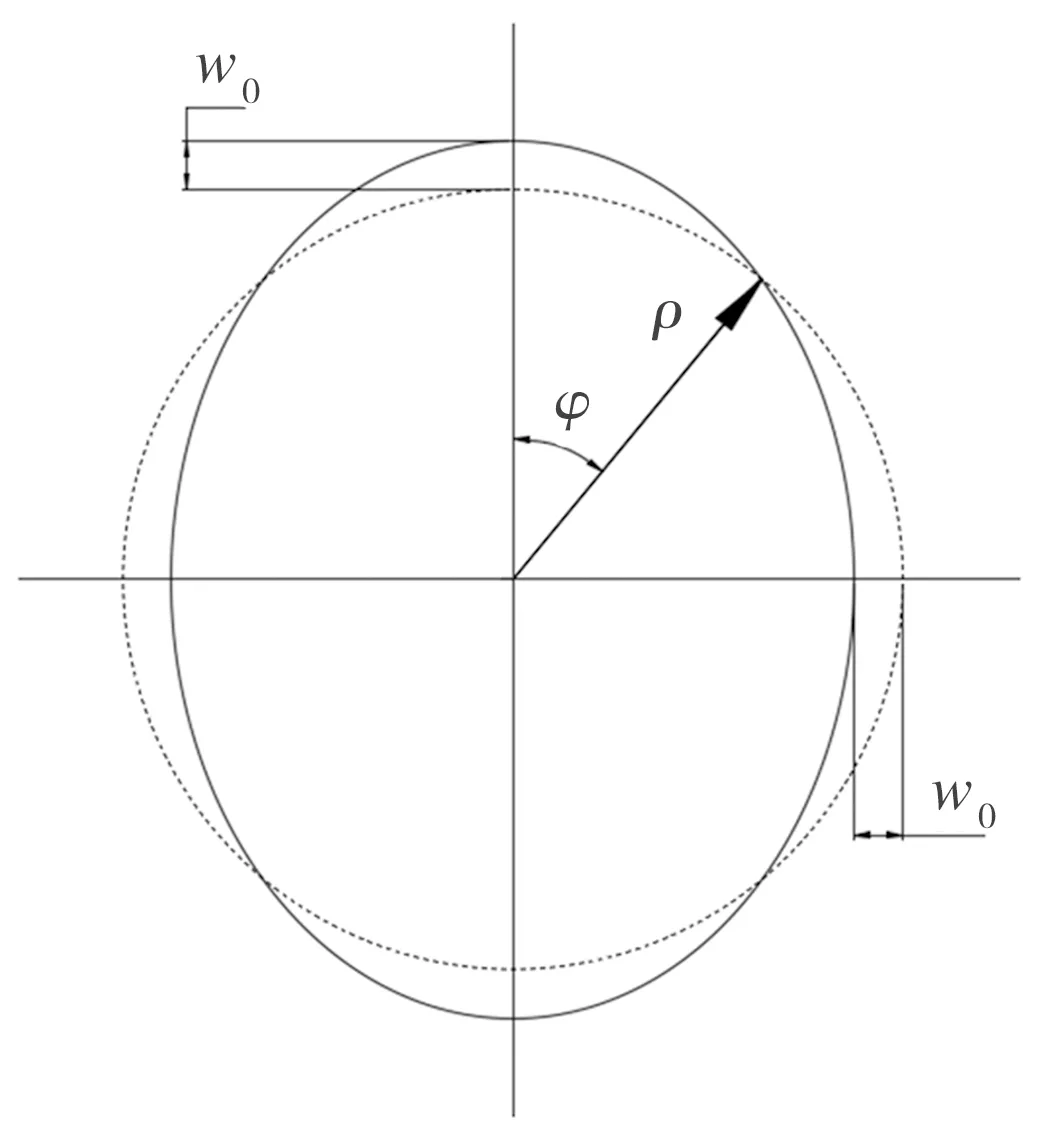
图1 柔轮中性层变形曲线

柔轮中性层曲线对应的变化方程为：

ρ(φ)=rm+w0cos2φ

(1)

式中，rm为柔轮中性层曲率半径，mm；w0为柔轮最大径向变形量，mm；φ为柔轮输出端转角,rad。

根据文献[3]可得，在塞入余弦凸轮之后，柔轮产生的变形可以分为以下三个部分。

(1)柔轮径向变形量(w)：

w=w0cos2φ

(2)

(2)柔轮周向变形量(v)：

(3)

(3)柔轮法向转角变形量(μ)：

(4)

1.2 柔轮齿廓设计

采用公切线式双圆弧齿廓作为柔轮齿廓，其基本齿形曲线如图2所示。从图2中可以看出，该齿形由凸圆弧AB、凹圆弧CD以及连接二者的一段公切线BC组成[4]。

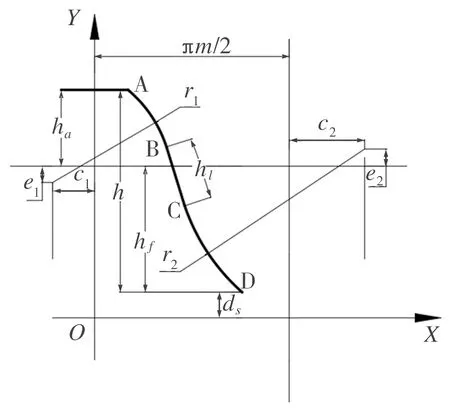
图2 公切线式双圆弧齿廓的齿形曲线

参考文献[4]，以弧长(s)作为变量建立柔轮的齿形方程分别为：

(1)凸齿廓AB的曲线方程

(5)

式中，s∈(0,l1)；α=sin-1[(ha+e1)/r1]；xo1=-c1；yo1=hf+ds-e1；l1=r1(α-δ)。

(2)公切线段齿廓BC的曲线方程

(6)

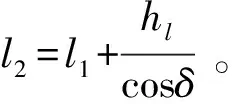
(3)凹齿廓CD的曲线方程

(7)

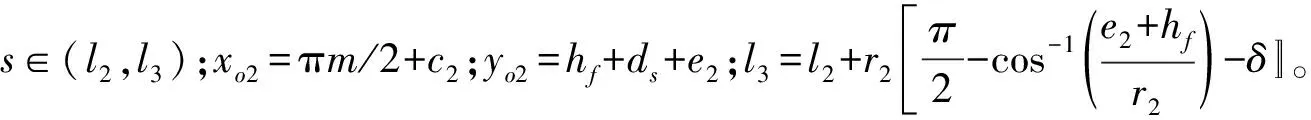
上述公式中柔轮齿形参数取值如表1所示。将表1中的参数值代入公式(5)、公式(6)和公式(7)，计算得到柔轮齿形如图3所示。由于轮齿在工作时总是绕着原点做旋转运动，因此在进行完整齿廓绘制时，可以按照平面坐标系下点绕原点的变换公式进行计算，即：

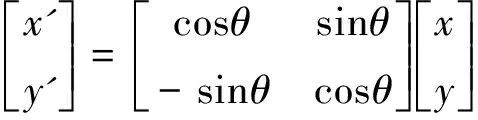
(8)

表1 柔轮齿形参数取值

式中，θ为点(x,y)绕原点旋转到点(x＇，y＇)所经过的角度。

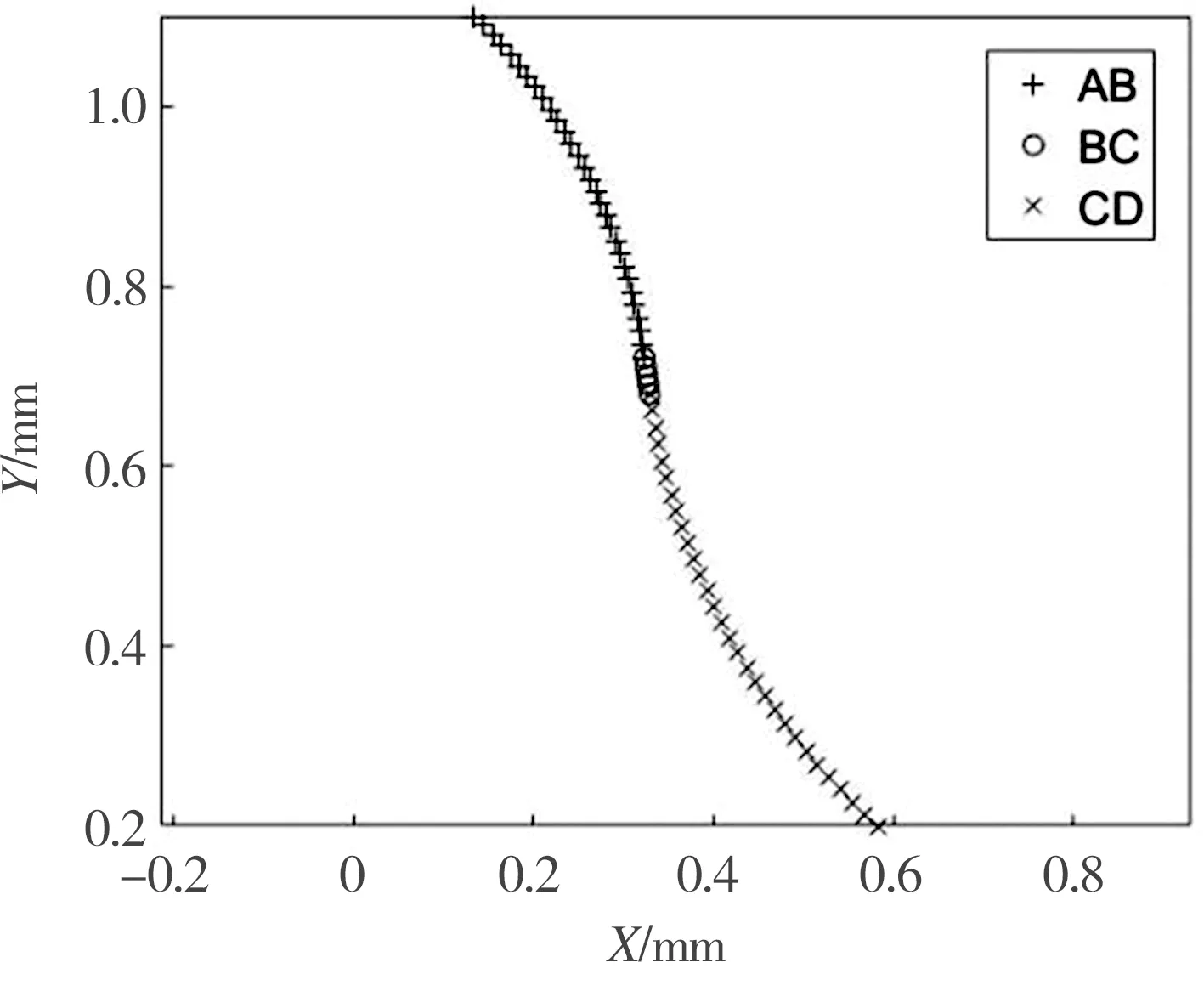
图3 柔轮齿形

由公式(8)计算得到柔轮完整齿廓如图4所示。

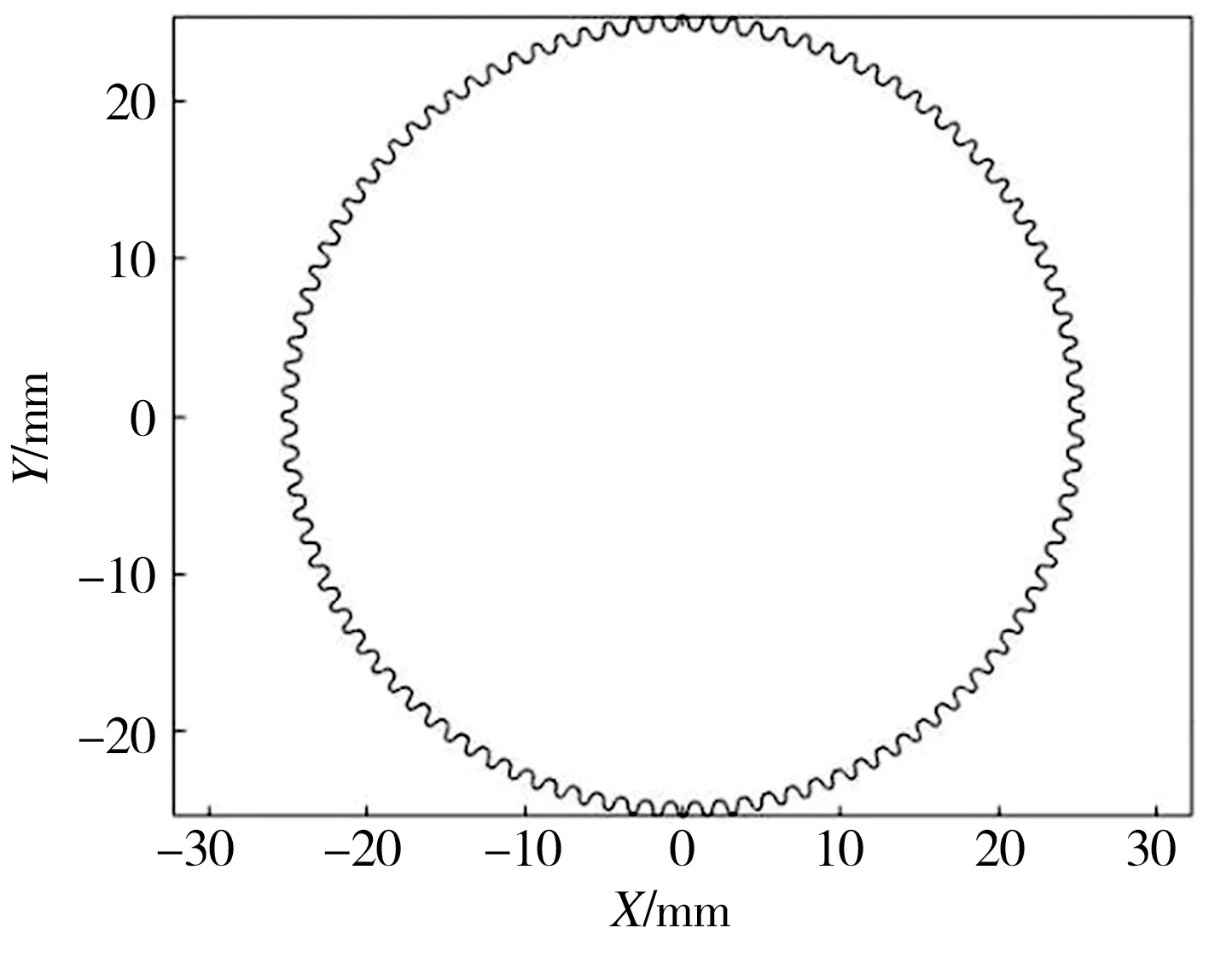
图4 柔轮完整齿廓

1.3 基于包络法的刚轮平面齿廓设计

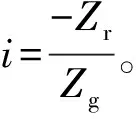
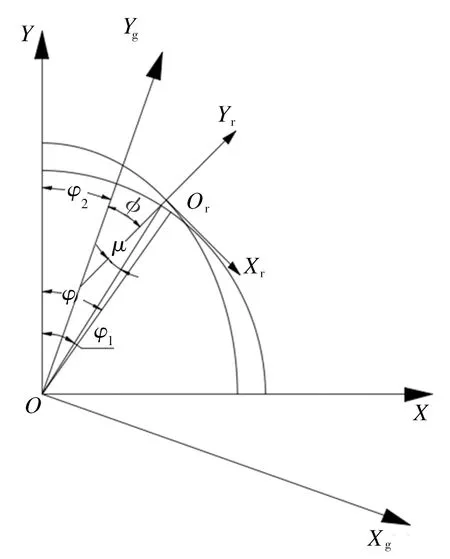
图5 谐波传动机构简图

基于包络理论求解刚轮齿廓时，具体可分为以下三个步骤。

第一步，转换坐标系。根据图5，可将柔轮齿形坐标数据通过转换矩阵M转化到刚轮坐标系下[6]。包络理论共轭方程为：

Xg=MXr

(9)

其中，柔轮齿廓方程为：

Xr=[xr(s,φ)yr(s,φ) 1]T

(10)

刚轮齿廓方程为：

Xg=[xg(s,φ)yg(s,φ) 1]T

(11)

刚柔轮坐标变换矩阵为：

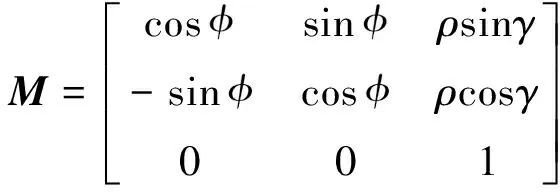
(12)

式中，γ为φ1与φ2之间的夹角,rad。

在柔轮坐标系中，柔轮齿形的参数方程为：

(13)

根据图5中的几何关系，可以得到：

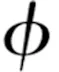
(14)

γ=φ1-φ2

(15)

考虑传动比可以得到：

(16)

由中线不伸长假设可以得到：

(17)

第二步，绘制曲线族。对柔轮运动转角φ进行离散化处理，可以绘制出不同转角对应的柔轮齿廓在刚轮坐标系中的位置变化图，如图6所示。

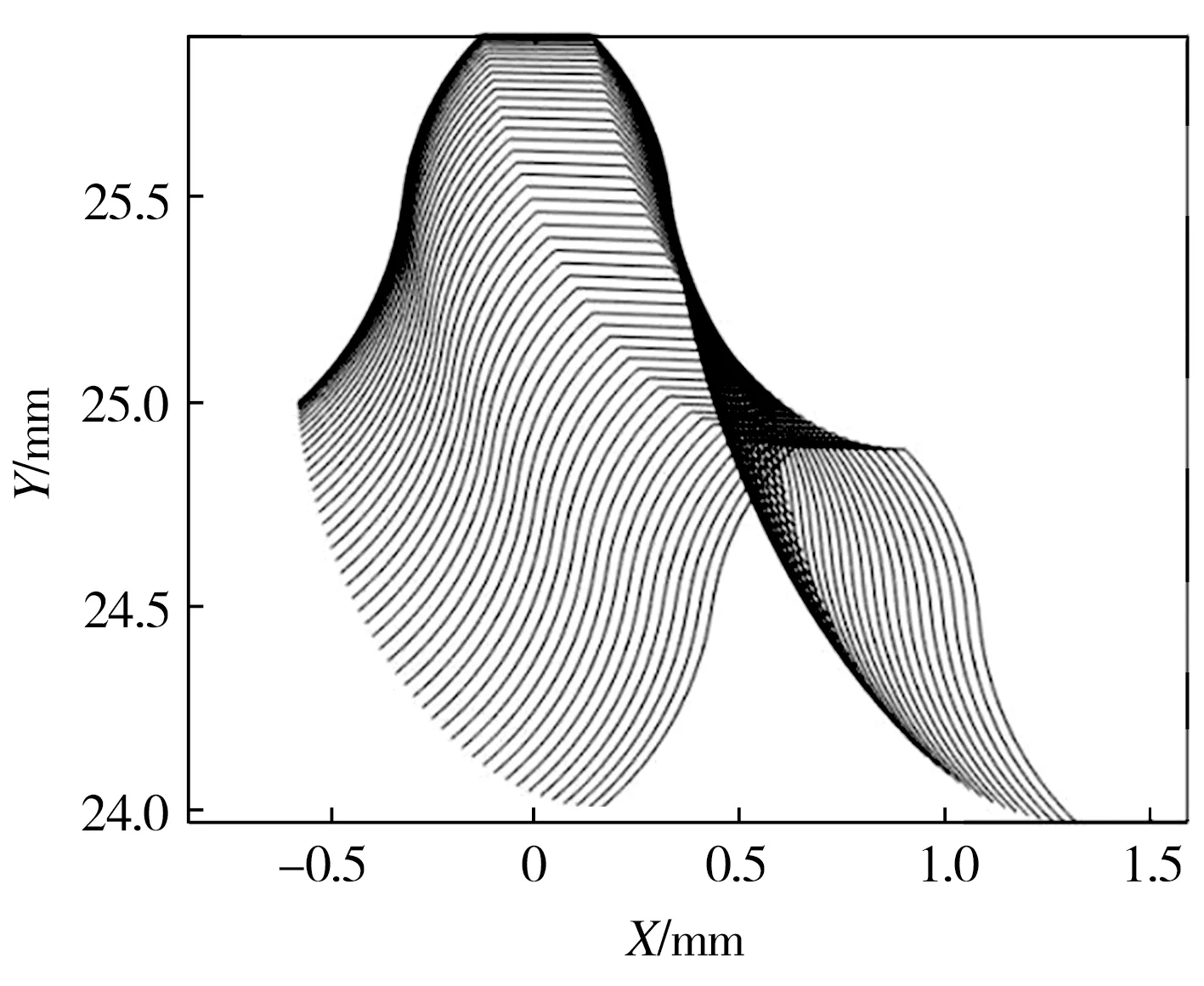
(a)局部图

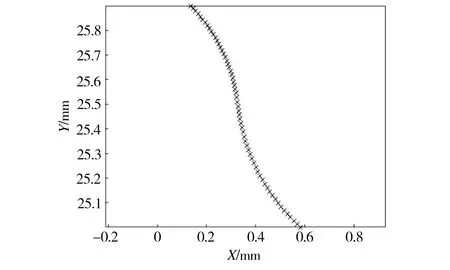
(a)刚轮单个齿廓线

2 谐波减速器刚轮空间齿廓建立

2.1 ANSYS有限元分析

本文所研究的谐波传动系统传动比为50，柔轮齿数为100，刚轮齿数为102，余弦凸轮的最大径向变形量为0.50 mm。首先，根据上述所设计的柔轮齿廓线，使用SolidWorks软件分别建立柔轮和余弦凸轮的三维模型，柔轮与余弦凸轮的装配体如图8所示。在实际装配过程中，余弦凸轮依靠外力塞入柔轮时，会导致柔轮发生弹性变形，内部产生预应力，而使用SolidWorks建立的三维模型不存在预应力，直接装配会使余弦凸轮和柔轮发生干涉[7]，因此，考虑到柔轮和余弦凸轮均为对称模型，各取其二分之一进行装配，使余弦凸轮外表面和柔轮内表面接触但不重叠。在余弦凸轮截面与柔轮截面之间添加平行配合，使用SolidWorks装配体视图中的测量工具，测量可得两截面之间的距离为4.69 mm。

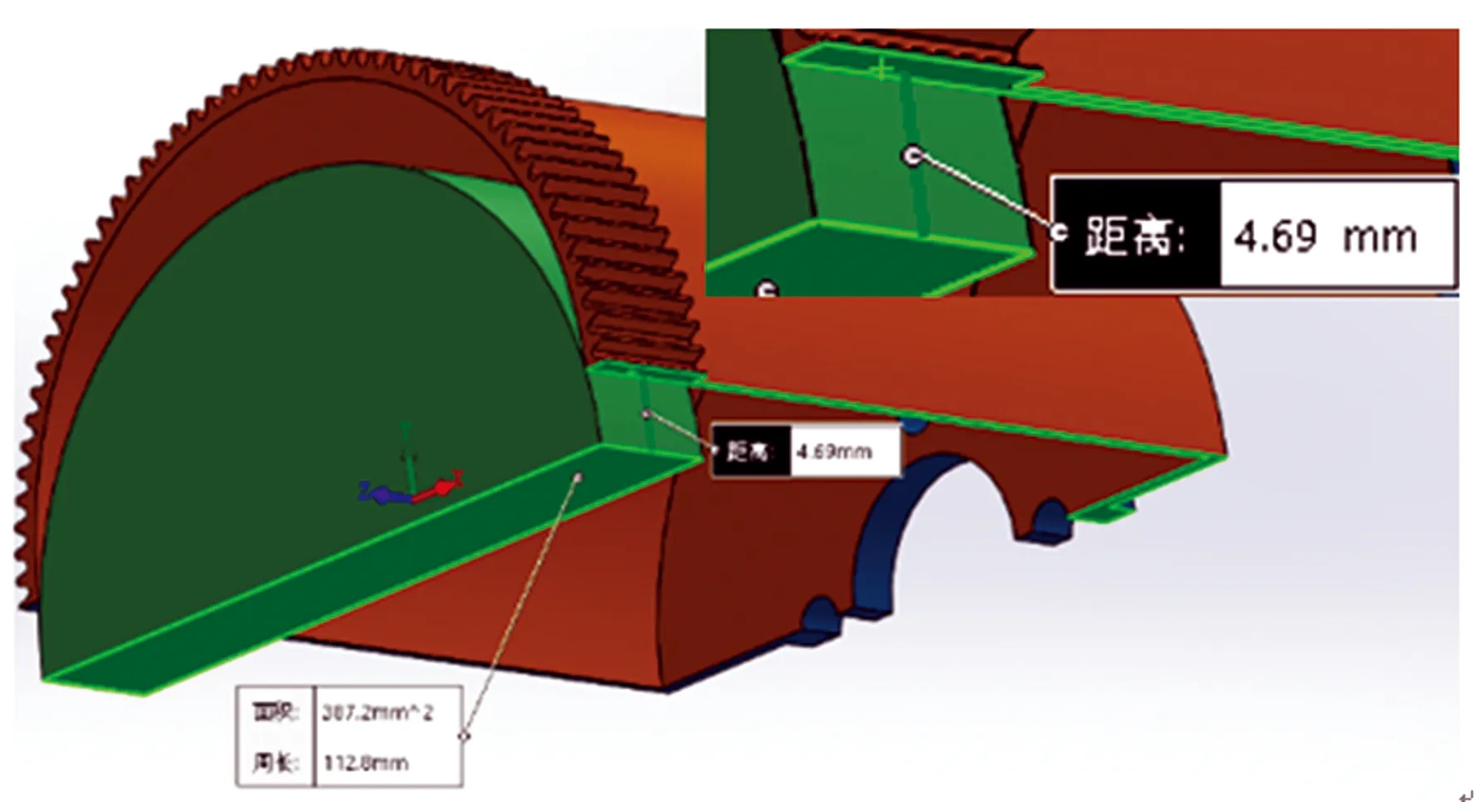
图8 柔轮与余弦凸轮的装配体

柔轮和余弦凸轮的网格划分如图9所示。在ANSYS Workbench软件中，使用扫掠划分方法对余弦凸轮进行网格划分，扫掠单元大小设置为1 mm，使用自动划分方法对柔轮进行网格划分，最终得到的网格模型节点数为108 619，单元数为54 832，单元最小边长为0.134 260 mm。

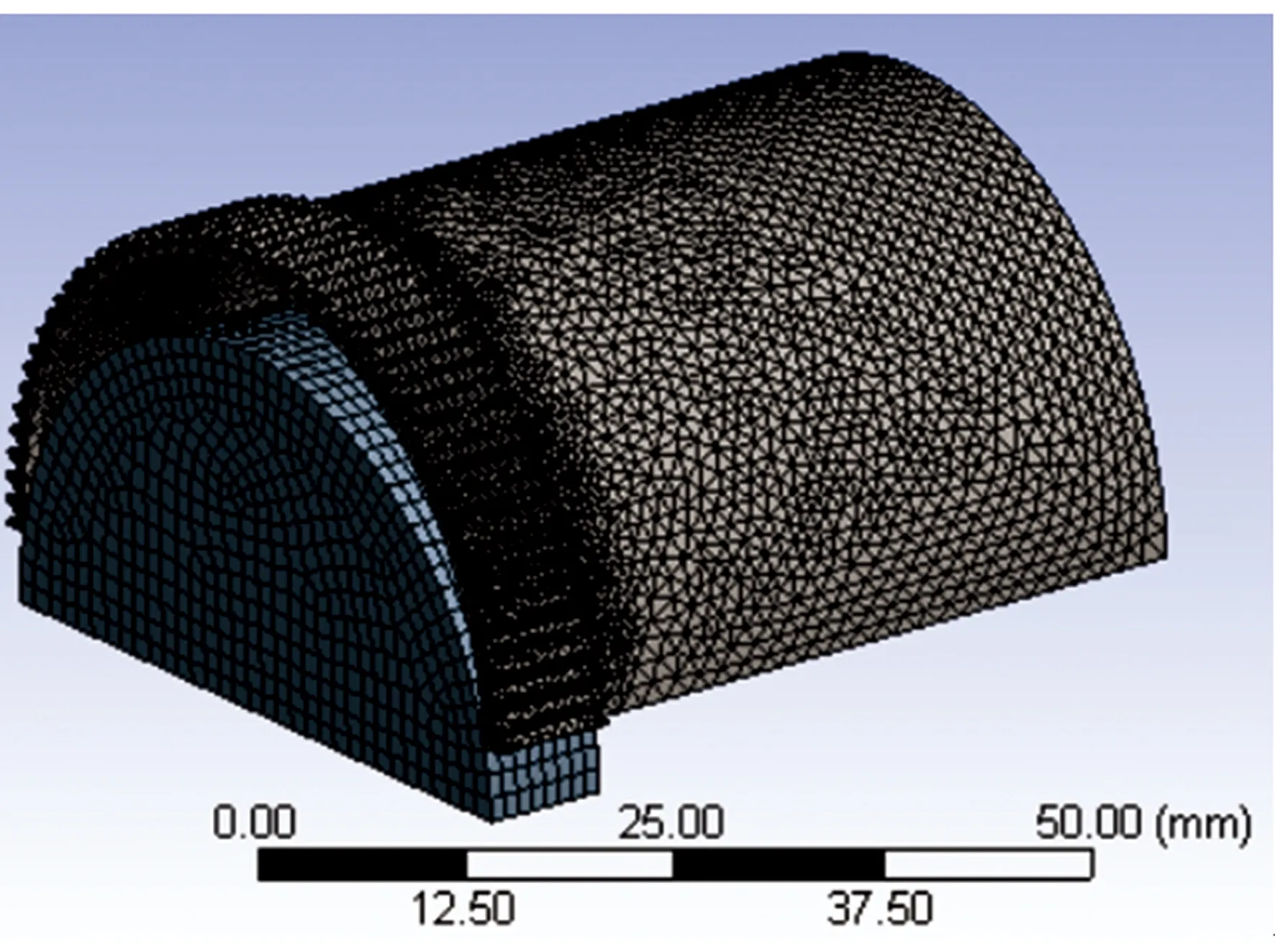
图9 柔轮和余弦凸轮的网格划分

设余弦凸轮与柔轮内表面的接触为摩擦接触，设摩擦系数为0.1。在柔轮截面处添加法向位移约束，在法兰处添加固定约束；对余弦凸轮添加一个Y轴方向大小为4.69 mm的位移，以此来模拟余弦凸轮塞入柔轮的过程。使用在柱坐标系上建立路径的方法，得到柔轮轮齿前端和后端中性层曲线的位移云图如图10所示。从图10中可以看出，前端中性层曲线位移的最大值为0.53756 mm，后端中性层曲线位移的最大值为0.49105 mm。柔轮轮齿前端和后端中性层曲线位移变化趋势相同，最大变形量与余弦凸轮的最大径向变形理论值0.50 mm接近，柔轮轮齿的前端最大变形量略大于后端最大变形量。

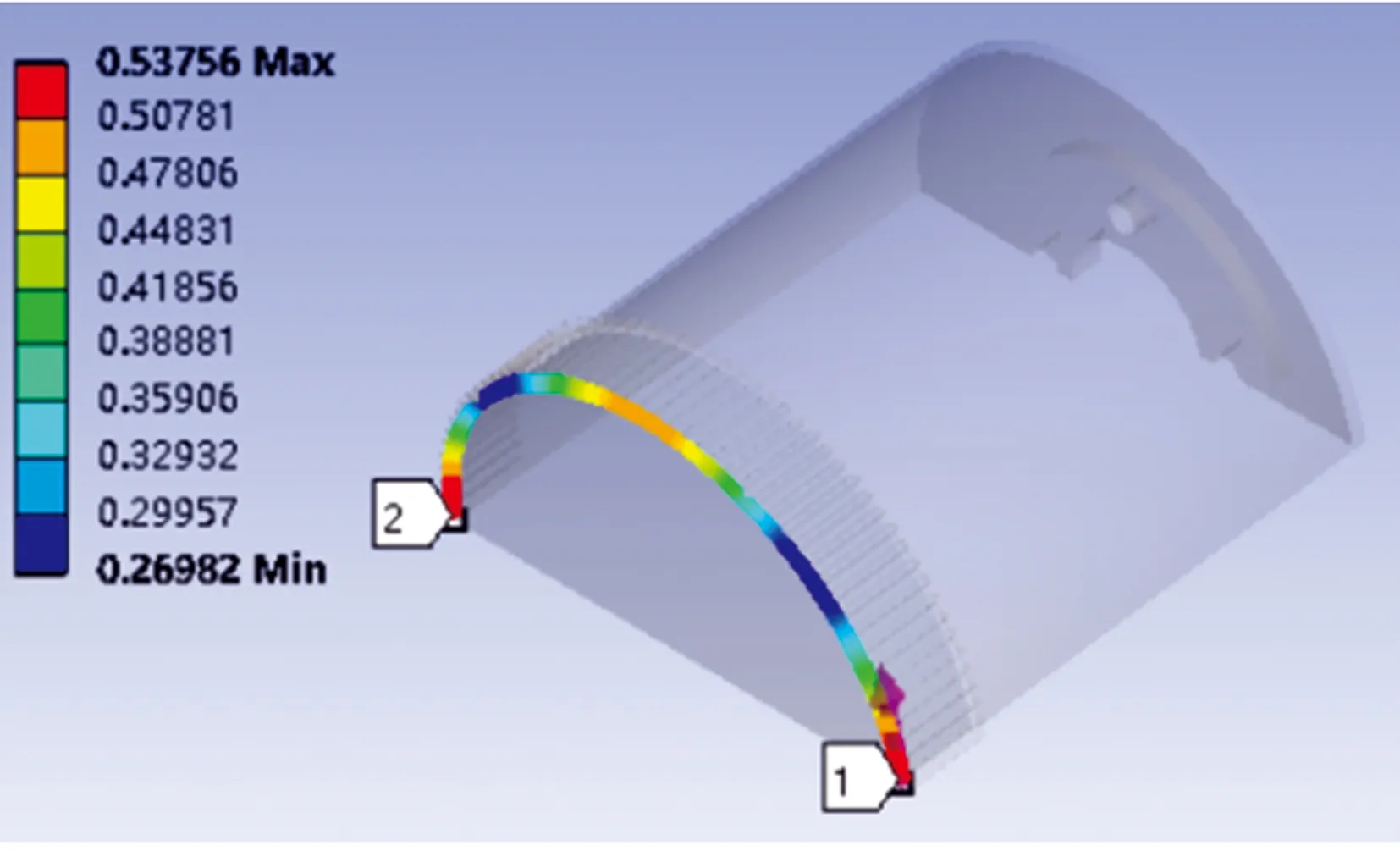
(a) 柔轮轮齿前端中性层曲线1

2.2 仿真数据的提取和函数拟合

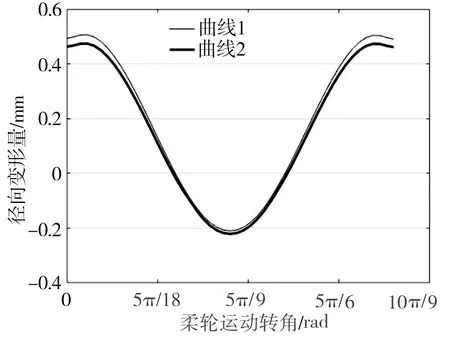
(a) 径向变形

借助Matlab中的CFtool工具箱，对仿真得到的曲线1和曲线2位移变形曲线进行函数拟合，得到其径向位移和周向位移变化方程，其中，曲线1和曲线2径向变形拟合方程w1和w2分别为：

(18)

曲线1和曲线2周向变形拟合方程v1和v2分别为：

(19)

与理论变形方程公式(2)和公式(3)相比，仿真得到的轮齿前后端中性层曲线的变形方程公式(18)和公式(19)更加贴合实际，更好地反映了柔轮前后端中性层曲线的变化差异。

2.3 刚轮空间齿廓建立

根据拟合仿真得到的轮齿前后端中性曲线变形方程，绘制出刚轮轮齿前端和后端的齿廓如图12所示。

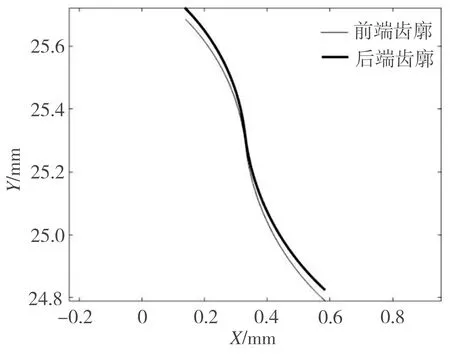
图12 调整后刚轮轮齿前端和后端齿廓

通过更改柱坐标系上路径的位置，采用同样的数据处理方法，可以得到刚轮轮齿前、后端之间各个截面处的齿廓，拟合可得修正后的刚轮空间完整齿廓模型如图13所示。采用包络法求解共轭齿廓，初步优化后的刚轮齿廓与柔轮运动轨迹能够较好贴合，从而使刚轮和柔轮的啮合率大幅提升，但是这样设计的齿轮在实际使用过程中，刚轮齿廓与柔轮齿廓之间难以存储润滑油，会加剧轮齿的磨损，同时轮齿容易因摩擦发热而出现膨胀卡死的现象，因此，在上述齿廓设计的基础上，还应该考虑齿侧间隙在整个传动系统中的影响。

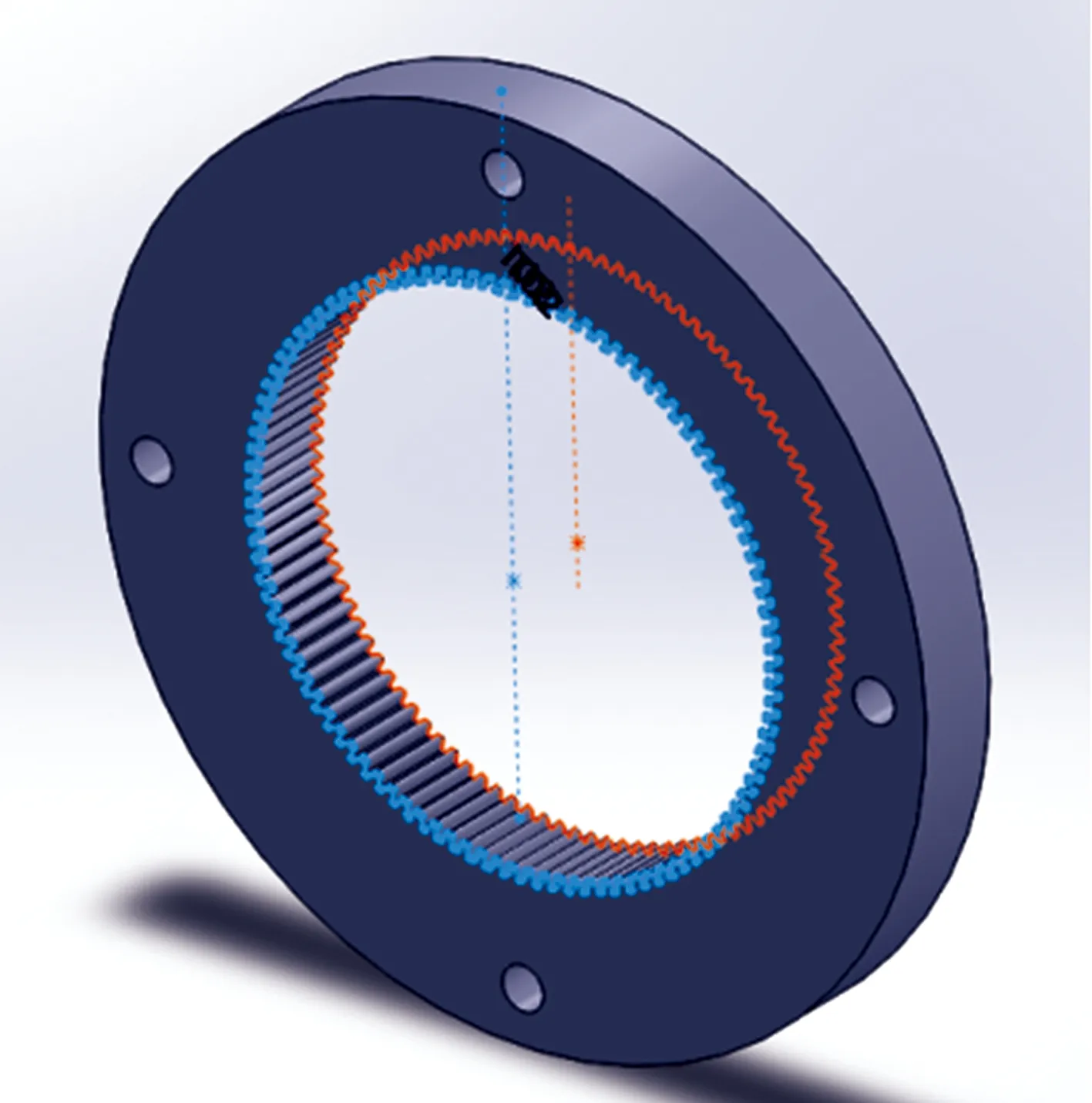
图13 刚轮空间齿廓模型

3 考虑侧隙的谐波齿轮系统动力学模型建立

齿侧间隙是指可能接触的啮合齿面上点对间的最小间隙，通常以周向侧隙表示[8]。如果侧隙为零，则谐波减速器运动传递精确，但是存在磨损大、散热难的问题，而侧隙过大，又会加大谐波传动系统的误差，影响系统稳定性。为了解决这个矛盾，对谐波减速器的刚轮空间齿廓进行改进，在刚轮齿廓与柔轮齿廓之间设定一个侧隙常数，对其进行动力学建模，然后使用PID调整器进行误差补偿。齿侧间隙会影响柔轮的弹性变形，进而影响到传动系统的运动传递。考虑弹性变形和扭转刚度在传动系统中的作用，建立谐波齿轮传动系统力学模型[9]如图14所示。图14中，θs(t)为电机输出端转角，rad ;Ts为输入端转矩，N·m;Id为电机转子连同波发生器的转动惯量，kg·m2;θi(t)为减速器输出端理想转角，rad;Δe(t)为减速器弹变扭转角，rad;K为减速器扭转刚度，N·m/rad;Tz为减速器输出端转矩，N·m;Iz为减速器输出端负载的转动惯量，kg·m2;θ0(t)为减速器输出端实际转角,rad。

图14 谐波齿轮传动系统力学模型

系统的传动误差E=θi(t)-θ0(t)，为了更好地反映谐波传动过程中的动力传递情况，将Ts折算到输出轴上记为Ti，Id折算到输出轴上记为Ii，Tgi记为输入端集中质量的惯性力矩，Tg0记为输出端集中质量的惯性力矩，Tp(t)记为弹变扭矩，建立谐波齿轮传动系统力矩平衡模型如图15所示。

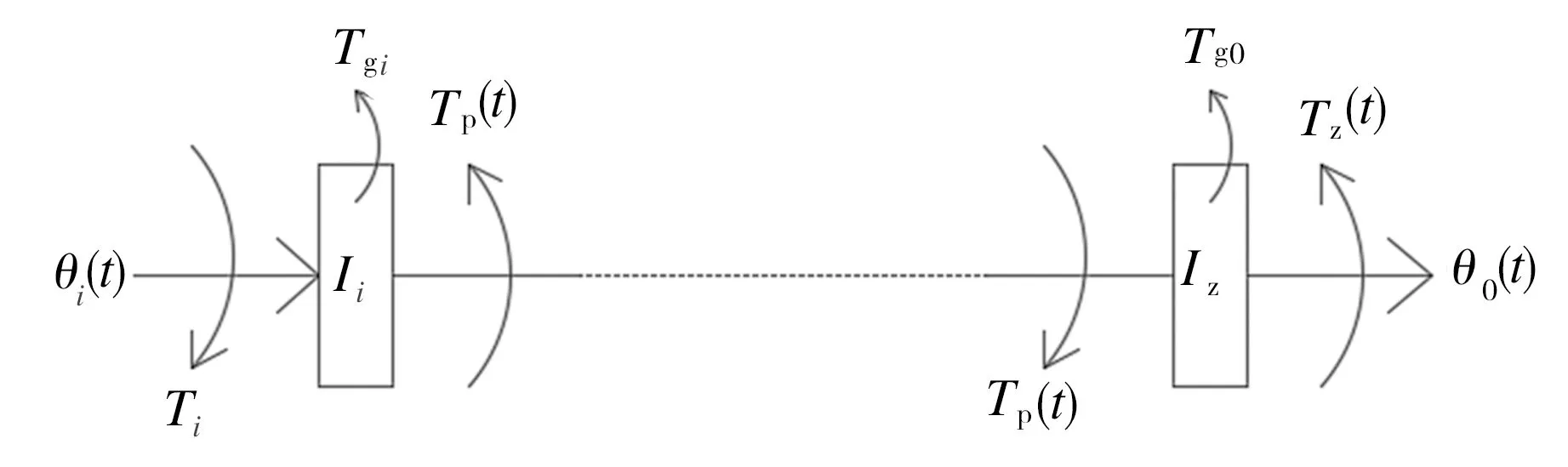
图15 谐波齿轮传动系统力矩平衡模型

根据力矩平衡关系，可列出减速器传动系统的动力学方程为：

(20)

式中，Tp(t)为减速器弹变扭矩，N·m，表示为：

Tp(t)=KΔe(t)

(21)

针对从电动机到负载的整个传动系统，可建立减速器弹变扭转角Δe(t)的数学模型：

Δe(t)=

(22)

式中，jt为齿侧间隙常数，μm。

4 谐波齿轮系统传动误差的补偿控制

将PID控制模块引入谐波传动系统，以达到对齿侧间隙引起的传动误差进行控制补偿的目的。PID调整器通过比较实际值与设计值得到系统偏差，然后将偏差通过比例、积分、微分的组合进行调整，从而得到补偿量。PID调节的微分方程式为：

(23)

式中，u(t)为补偿量，rad；e(t)为系统弹变扭转角的偏差值，rad；kp为比例系数；Ti为积分系数；Td为微分系数。

4.1 系统控制方框图

将公式(21)代入公式(20)中，可得：

(24)

由此得到减速器传动系统的传递函数为：

(25)

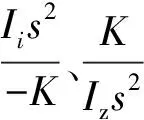
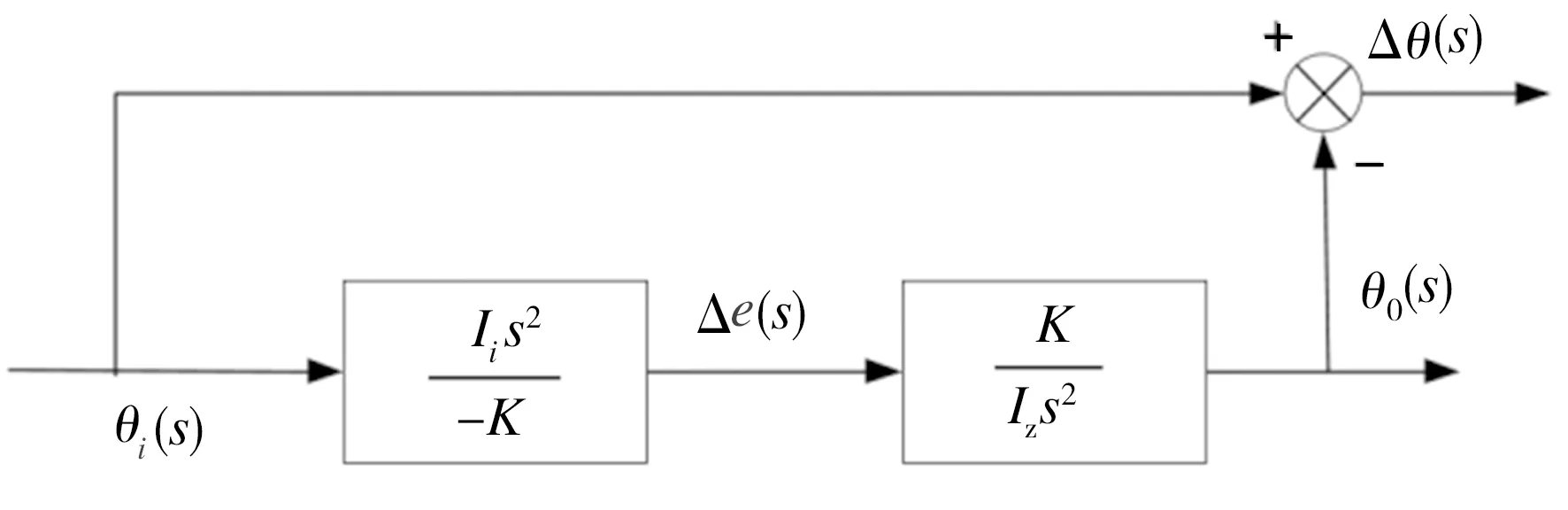
图16 不包含补偿的系统方框图

在图16中添加PID控制模块之后的方框图如图17所示。

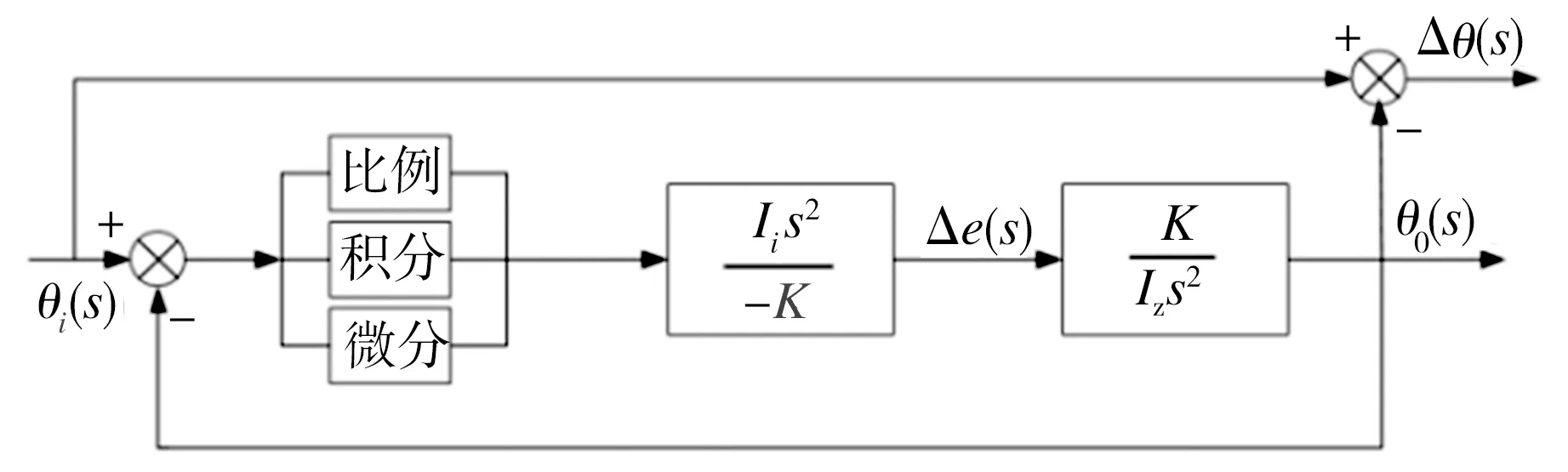
图17 加入补偿后的系统方框图

4.2 传动误差仿真分析

本文所研究的谐波传动模型输出端转动惯量为0.000 19 kg·m2，输入轴转速为2000 r/min，输入转矩为24 N·m，负载力矩为50 N·m，扭转刚度为55000 N·m/rad，经查齿轮侧隙表，侧隙应设置为105 μm。

将公式(21)代入公式(20)中的第二式可得：

(26)

根据公式(22)和公式(26)，结合图16中的系统方框图，对补偿前传动系统进行simulink仿真。用斜坡输入代表减速器输出端理想角位移函数，该函数以时间为自变量、角位移值为因变量，由减速器输入轴转速(n)和减速器的传动比(i)可得：

(27)

本次仿真中的谐波减速器处于单向匀速转动状态，设置仿真时间为4 s，斜坡输入函数图像如图18所示。

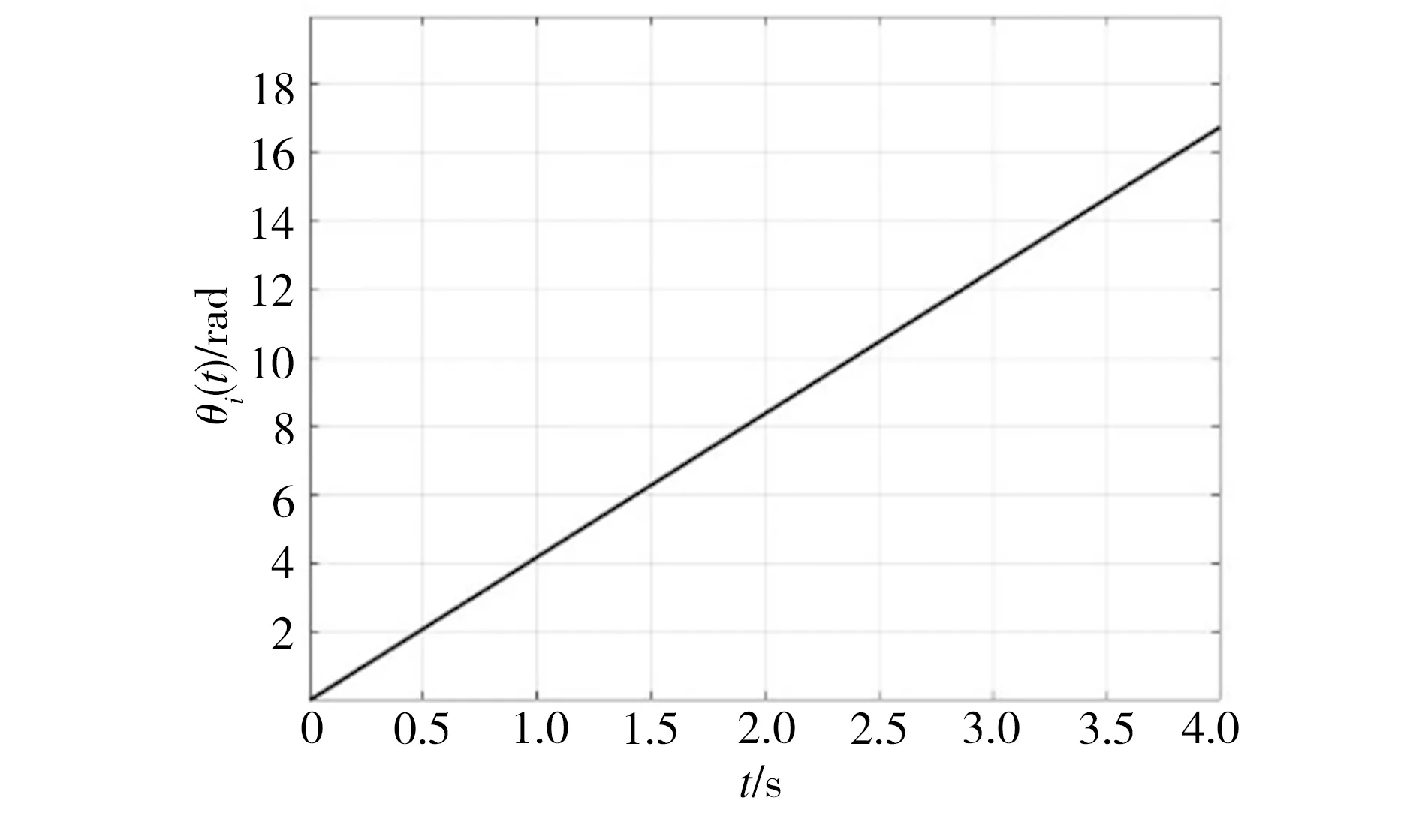
图18 斜坡输入函数图像

仿真时用Dead Zone模块表示侧隙模型，计算侧隙对应的弧度，设置Dead Zone参数范围为[-0.0021,0.0021]，其输出即为弹变扭转角Δe(t)，仿真模型及仿真结果如图19所示。从图19中可以看出，在0～4 s内，传动误差在-0.010～0.010 rad范围内变化，且有逐渐增大的趋势。

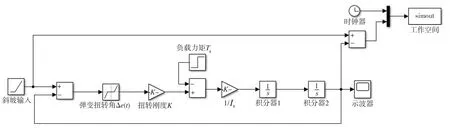
(a)未加PID模块的simulink仿真模型

设置PID控制器中的控制系数分别为：Proportional(P)=1、Integral(I)=1、Derivative(D)=0.005，得到控制补偿之后的传动误差变化曲线如图20所示。从图20中可以看出，PID补偿模块能够较好地调节传动误差，在0～0.2 s内，误差范围明显缩小，在0.2～1.5 s内，误差逐渐向0值靠拢，之后在0值附近做小幅度摆动。