确定函数型数据主成分个数的自适应加权截断法

田 密，罗幼喜

(湖北工业大学理学院，湖北 武汉，430068)

函数型数据[1-2]具有函数的特征，对其处理不再是把单个数据看作样本，而是将数据拟合为一条函数曲线作为样本进行分析。由于函数型数据理论上隶属于无穷维空间上的数据，因此实际运用中通常需要对其进行基函数展开降维处理。目前常用的基函数有两类：第一类是给定的基函数，如Zhou等[3]、Lian等[4]对函数型变量使用的B样条基展开，但是这种基函数与数据是独立的，不随数据的改变而发生变化，因此难以确定原始数据的主要信息由多少个基函数决定；第二类是结合样本数据形成的基函数，如Shin等[5]、Zhang等[6]使用的函数型主成分基展开，其中所选取的主成分基是由数据所驱动，它随着数据的不同而相应发生改变，并且能够解释函数型变量变差的百分比，因此这类主成分基展开更具有实际意义。然而，对函数型数据采用主成分基展开也涉及到基函数的个数K的确定这一重要问题。K的选取表现为估计的偏差与方差之间的平衡:K越大，估计的偏差越小，而方差越大；反之，K越小，估计的偏差越大，而方差越小。

众多研究者从不同角度提出了确定函数型数据主成分个数的相关准则。Rice等[7]提出依据方差解释百分比(percentage of variance explained, PVE)对主成分数量进行截断；Müller等[8]也采用此方法确定函数型主成分的个数;但是Zhu等[9]研究指出，尽管基于PVE的主成分基截断操作简单，但这种方法仅考虑了特征值的大小，而对于许多复杂问题，函数型主成分的个数对响应变量的影响并不仅仅与特征值大小有关。Su等[10]用PVE法确定主成分基个数并应用于假设检验，证实了PVE并不是用于检验的最佳标准，于是提出关联变异指数(association-variation index，AVI)这一概念，并由此建立关联变异解释百分比准则(percentage of association-variation explained，PAVE)替代PVE用于函数型主成分的排序和选择。虽然PAVE法能够考虑到回归模型中函数型变量对响应变量的影响，但这种方法忽略了由于特征值迅速衰减导致的函数型协变量的主要变异。

鉴于以上方法的不足，本文提出一种新的自适应加权截断法用于函数型主成分个数的选择。该方法首先分别基于PVE和PAVE对函数型数据的主成分基进行排序和选择，然后对两个方法截断出的基函数个数进行加权，通过求解最小化估计误差获得最优权重参数，从而最终确定主成分基展开项数。该方法不仅考虑了由于特征值迅速衰减导致的主要变异，还将函数型协变量和响应变量之间的关联纳入选择标准中，并且权重的自适应选择使得最后的主成分数量恰当，进而使估计的偏差与方差之间能达到相对平衡。

1 模型与算法

1.1 函数型回归模型与主成分基展开

假设响应变量Y为标量，X(t)是定义在某个区间T上的函数型协变量，满足E(X(t))=0，E(X2(t))<∞。考虑一元函数型线性回归模型：

(1)

式中：t∈T，不失一般性，可取T为[0,1]；β0为未知的截距项；β(t)为未知的光滑斜率函数；ε为零均值、方差有限的随机误差项，且与X(t)独立。

本文采用主成分基函数对函数型变量X(t)和函数系数β(t)进行扩展。首先，函数型变量的协方差矩阵有一个谱分解：

其中，Φ(s,t)表示协变量的协方差函数，λ1≥λ2≥…≥0是算子Φ的有序特征值，满足

{φk(t)∶k=1,2,…}构成均方可积函数空间L2(T)中的一组标准正交基，即函数型数据X(t)的主成分基函数，再根据Karhunen-Loeve定理有

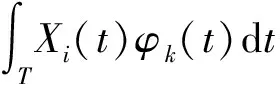
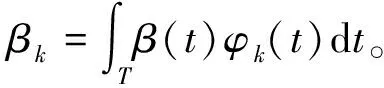
对X(t)与β(t)都用主成分基展开，则式(1)变为：

(2)

用最小二乘法最小化如下目标函数：

(3)

由于实际应用中随机函数X(t)是未知的，所以需要通过观测到的样本{X1(t),X2(t),…,Xn(t)}来估计未知的特征根λk和主成分得分ξik，故需要估计出协方差函数Φ。

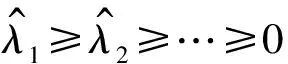
于是改变为最小化如下目标函数：

(4)

在式(4)中，为了达到降维的目的，需要根据一些准则确定主成分基函数的个数。

1.2 函数型主成分截断个数的确定

1.2.1 基于PVE和PAVE的主成分选择

首先通过方差解释百分比PVE和关联变异解释百分比PAVE分别截断出函数型主成分个数K1、K2。

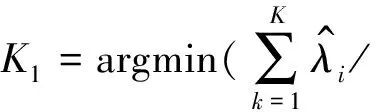
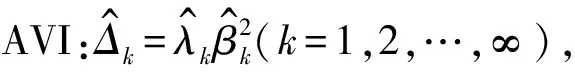
1.2.2 权重α的确定

对上述确定的截断个数K1和K2分别取权重(1-α)、α后相加，得(1-α)K1+αK2，但由于截断数应为整数，因此采用以下公式对(1-α)K1+αK2取整，得到截断个数K：

(5)

式中：Θ[· ]表示向下取整。

权重α从(0,1)区间选择，每一个权重依据式(5)都有一个截断个数K，即为对应的主成分基函数个数。将函数系数β(t)和函数型协变量X(t)均通过主成分基展开后，再对函数系数进行估计，得到估计误差

挑选出使估计误差最小的权重α，若得到的权重不止一个，则取接近于0. 5的值，因为α接近于0.5不会使截断个数过大或者过小。过大的截断个数可能会使数据出现过拟合的现象，而过小的截断个数可能会使得估计结果损失过多的样本信息，因此权重表示为

该权重对应的K值即为通过本文方法最终得到的主成分截断个数，相应地将目标函数式(4)转换为：

(6)

2 蒙特卡罗模拟研究

2.1 模拟数据

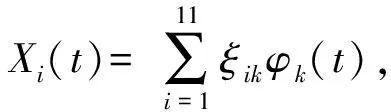
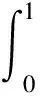
2.2 权重

本文方法需要选择出自适应的权重，不妨令α∈[0.1,0.2,…,0.9]。通过最小二乘法对回归系数进行估计，用均方误差(RMSE)评价估计误差。

通过对以上情形的模拟得到不同权重对应的函数系数估计误差，由于篇幅所限，图1仅给出阈值为0.95的模拟结果，图中实心点表示对应的权重使得均方误差RMSE达到最小，如果实心点多于1个，则靠近0.5的权重即为所求的α值。

从模拟结果可知：在大约55.56%的情形中得到的权重小于0.5，尤其是样本量n=50的情形,α全部小于0.5，权重小于0.5说明此时在本文方法中方差解释百分比所起的作用较大；在大约27.78%的情形中权重大于0.5，其中以样本量n=500、σ2=1的情形为主，说明此时关联变异解释百分比所起的作用更大；在大约16.66%的情形中权重为0.5，此时方差解释百分比和关联变异百分比在本文方法中起着同样的作用。

2.3 三种方法的比较

将分别采用三种方法的模拟结果进行对比，主成分截断个数的平均值如表1所示。可以看出，除去个别情形外，通过方差解释百分比截断的主成分个数都多于基于关联变异解释百分比的截断个数，而采用本文方法得到的截断个数处于二者之间，主成分数量比较恰当，对于函数协变量可以避免出现过拟合或者损失过多样本信息的情况。

对自适应加权截断法的模拟结果进行统计：当阈值分别为0.95、0.97、0.99时，对应的主成分基截断个数总平均值分别为5.828、6.101、7.287，即随着阈值的增大，主成分基个数也随之增多；当σ2分别为0.5和1时，对应的主成分基截断个数总平均值分别为6.353和6.457，即随着误差的增大，主成分基个数也有增大的趋势；然而，当样本量n分别为50、100、500时，对应的平均截断个数为7.114、6.419、5.684，即随着样本量的增多，通过本文方法截断的主成分个数在减少。

(a)n=50,σ2=0.5 (b)n=100,σ2=0.5 (c)n=500,σ2=0.5

表1 三种方法的主成分截断个数平均值

为了进一步说明自适应加权截断法的优越性，比较三种方法对函数系数β(t)的估计，得到表2的结果。从表2可以看出，本文方法的估计误差均小于其他两种方法的对应值，表明其对函数系数的估计精确度有所提高。对自适应加权截断法的结果进行统计：随着阈值由0.95逐渐增至0.99，β(t)的平均估计误差也随之增大，从0.3409到0.3759再到0.5032；当σ2分别等于0.5和1时，β(t)的平均估计误差分别为0.2665和0.5466，即平均估计误差随着随机误差的增大而增大；当样本量n分别为50、100、500时，β(t)的平均估计误差分别为0.7974、0.3656、0.0567，即随着样本量的增多，函数系数的估计误差在减少。

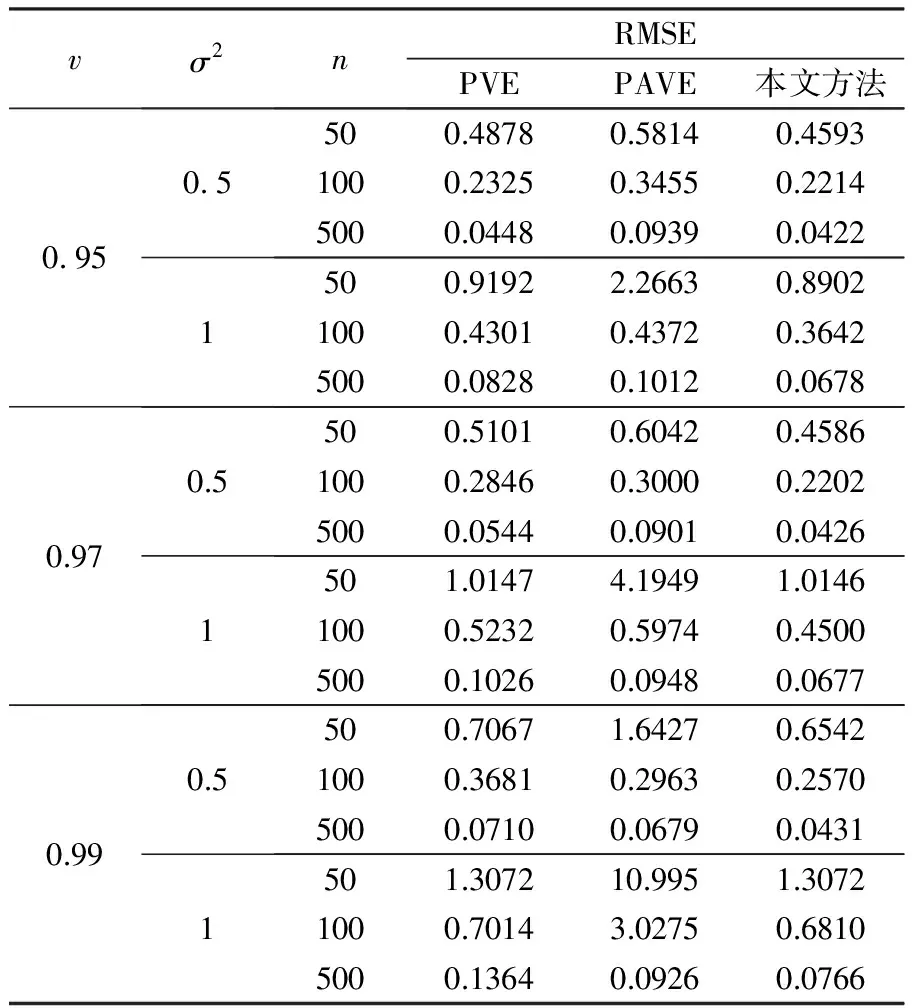
表2 三种方法对函数系数β(t)的估计误差RMSE

2.4 自适应加权截断法的拟合结果

将本文方法拟合的曲线与函数型回归曲线β(t)进行比较，得到阈值分别为0.95、0.97、0.99的结果。限于篇幅，图2仅给出v=0.95时的拟合效果，由对比结果来看，在各种情形下，本文方法都能很好地拟合函数型回归曲线β(t)。

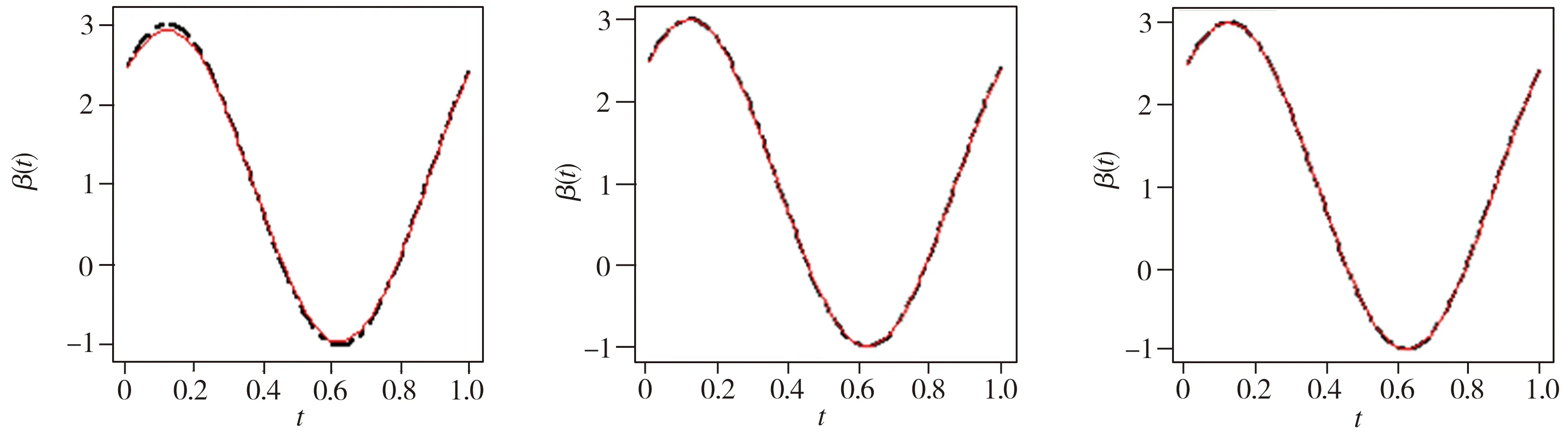
(a)n=50,σ2=0.5 (b)n=100,σ2=0.5 (c)n=500,σ2=0.5

3 实际数据分析

本节通过弥散张量成像(diffusion tensor imaging, DTI)数据对新方法进行展示和比较分析。Goldsmith等[11]、田茂再等[12]都曾对该数据进行过研究，原始数据可以在Huang等[13]编写的R软件包“Refund”中下载。

弥散张量成像数据是医学研究数据，该数据集包含了382个样本。通过核磁共振成像记录大脑中水分子沿胼胝体方向弥散的轨迹，再根据部分各向异形图在白质束上的位点，得到93个数据。同时，实验还记录水分子沿着右皮质脊髓束方向弥散的轨迹，得到55个数据，由此可以得到两个函数型变量。另外，每位患者都做了一个有节奏的听觉系列加法测试(paced auditory serial addition test, PASAT)，测试结果为0到60不等的得分。本文分析的目的是量化各向异形图沿胼胝体方向对响应变量PASAT分数的影响。

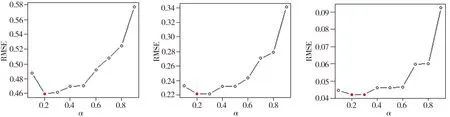
将382个样本数据进行预处理，对余下的236个样本数据建立一元函数型线性回归模型，以胼胝体数据为函数型协变量，以PASAT得分为标量型响应变量。在阈值分别为0.95、0.97、0.99的情况下，通过自适应加权截断法获取使估计误差RMSE最小时的权重，如图3所示。由图可见，阈值为0.95时，权重取0.2和0.3可以使RMSE最小；阈值为0.97时，权重取0.2、0.3及0.4使得RMSE最小；阈值为0.99时，权重取0.8和0.9使得RMSE最小。因此，对于弥散张量成像数据，在本文提出的主成分基个数的自适应加权截断法中，阈值为0.95和0.97时，方差解释百分比的贡献要大于关联变异解释百分比，而阈值为0.99时恰好相反。

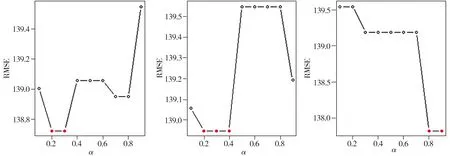
(a)v=0.95 (b)v=0.97 (c)v=0.99

比较三种方法对弥散张量成像数据的预测效果，同样采用RMSE指标计算估计误差，结果见表3。由表3可见，本文方法的估计误差要稍小于基于PVE和PAVE的估计误差，表明新方法可以提高预测精度，并且本文方法截断的函数型主成分个数介于其他两种方法截断的主成分个数之间，不会因主成分过多导致过拟合，也不会因主成分太少导致损失过多的样本信息，进而使得估计的偏差与方差达到相对平衡。

表3 三种方法对于DTI数据的预测误差和截断结果

4 结语

本文针对函数型数据主成分基函数的个数选取提出了一种新的截断方法。首先通过方差解释百分比和关联变异解释百分比准则对函数型主成分进行排序和截断，分别得到截断个数K1、K2，然后对K1、K2进行加权求和，并通过优化算法获得使估计误差达到最小的最优权重，进而得到最终的主成分展开截断项数。新方法不仅考虑了函数型协变量由于特征值迅速衰减导致的主要变异，还将协变量和响应变量之间的关联纳入选择标准中，且权重α的选择使得最后的截断个数不会过大或过小，进而使估计偏差与估计方差处于一个相对平衡的状态。

蒙特卡罗模拟结果显示，在不同的样本量、随机误差和阈值条件下，本文方法对未知函数系数的估计精度和稳定性整体上都优于只用方差解释百分比准则和只用关联变异解释百分比准则的主成分截断方法。同时，随着阈值或者随机误差的增大，函数型主成分的截断个数也在增多，并且函数系数的估计误差也有随之增大的趋势；但函数型主成分的截断个数以及对函数系数的估计误差随着样本量的增大而减小。

本文方法在弥散张量成像数据分析中的实际应用也显示，其不仅能量化各向异形图沿着胼胝体方向对PASAT分数的影响，而且在预测效果上也优于其他两种方法。