筒形柔轮的结构优化与有限元分析

□ 陈 博 □ 闫 恒 □ 张建荣 □ 杨 健

1.兰州理工大学 机电工程学院 兰州 730050 2.中航工业兰州万里机电有限责任公司 兰州 730070

1 研究背景

谐波齿轮传动广泛应用于航空、航天、深海等国防设备的精密仪器中。谐波减速器在传动精度、传动比、回转误差、使用空间、体积、质量等方面,与普通齿轮减速器相比有很大优势[1]。在传递扭矩等性能不变的前提下,谐波减速器筒身长度缩短,可以使体积及质量减小,在战斗机、无人机、卫星等对质量和体积有较高要求的项目中有重要意义。然而,随着谐波减速器柔轮筒长的缩短,也带来了一些不可避免的问题。如图1所示,柔轮的应力随着筒长的缩短而急剧增大,同时导致柔轮齿圈内部与柔性轴承自然贴合张角由θ2增大到θ1,柔轮轮齿偏斜严重,重合度降低,柔轮整体寿命缩短。通过研究,使柔轮筒长缩短,并有效弱化或消除以上问题,是谐波减速器柔轮发展的方向之一[2]。

在谐波减速器柔轮结构优化方面,已有学者进行了大量研究,并取得了一定的研究成果。柔轮结构优化时,分析柔轮长径比、齿根壁厚、齿宽、啮齿对数、最大径向变形量、杯底倒角等结构参数对柔轮变形及应力的影响,通过设计正交试验进行多目标优化[3-4]。

▲图1 柔轮齿圈内部与柔性轴承自然贴合张角对比

柔轮结构优化的目的是消除柔轮齿圈局部应力集中。部分学者对目前固有的柔轮结构做出了大胆设计,以解决柔轮应力集中问题。王迪[5]在原杯形柔轮的基础上提出三种新型柔轮结构,分别为直线圆角回型、“之”字形、直线直角回型且保持轴向尺寸不变,通过接触分析对这三种新型柔轮结构进行性能排序。王新等[6-7]基于王迪提出的三种新型柔轮结构,根据半无矩理论,对三种新型柔轮进行空载情况下的等效应力与应变分析,得出直线直角回型柔轮结构性能优于其它两种柔轮结构。王巨涛等[8]提出一种波纹型柔轮结构,可以减小由波发生器装配进柔轮时产生的张角,提高柔轮与刚轮啮合时的径向重合度。

笔者对原长筒形柔轮结构进行大胆改进,通过缩短轴向尺寸,将筒底圆角改为双圆弧形,进而对柔轮关键结构参数进行优化,既缩短了筒体长度,又可以达到减小最大应力的目的。结构改进后柔轮局部放大图如图2所示。

▲图2 结构改进后柔轮局部放大图

2 建模

柔轮尺寸如图3所示,柔轮结构参数见表1。

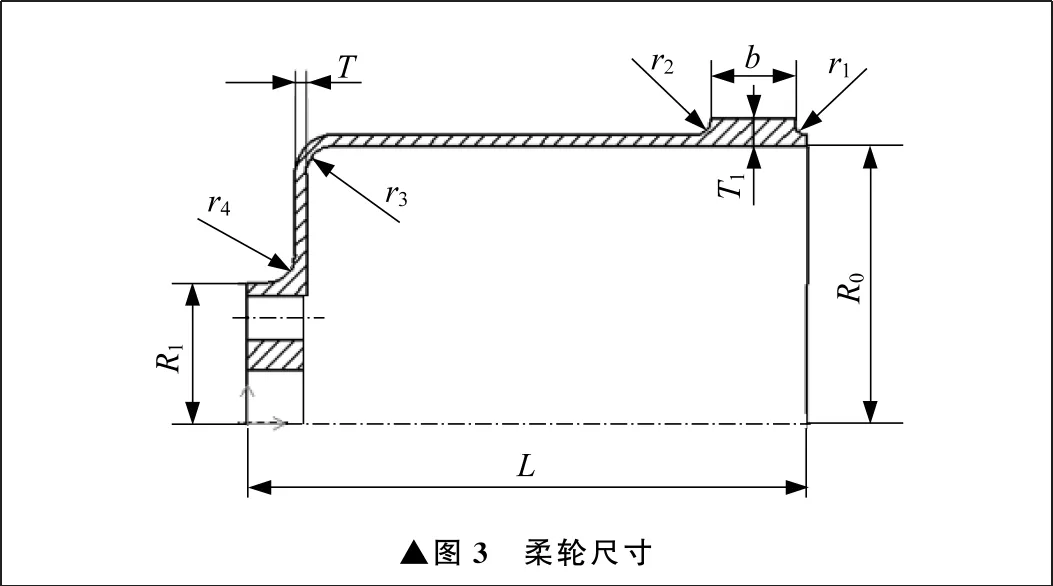
▲图3 柔轮尺寸

表1 柔轮结构参数 mm

结构改进后柔轮尺寸如图4所示,原筒底倒角改为双圆弧,圆角尺寸不变,柔轮整体长度缩短为27 mm。

▲图4 结构改进后柔轮尺寸

采用SolidWorks软件对长筒形柔轮和结构改进后柔轮进行三维建模,如图5所示。

▲图5 柔轮三维模型

将柔轮三维模型保存为.x_t格式,导入ANSYS Workbench软件,对柔轮三维模型进行网格划分。网格划分时,采用六面体单元对长筒形柔轮筒体、结构改进后柔轮双圆弧筒体、柔轮齿圈、柔轮筒底底部进行扫掠网格划分。由于柔轮筒底法兰与输出端采用螺栓固定,因此采用自由网格划分柔轮筒底法兰部分[9]。

谐波减速器利用柔轮的不断变形来传递扭矩,因此,柔轮可作为柔性体,与柔轮接触配合的波发生器可看作刚体,波发生器与柔轮的接触为刚柔接触。柔轮筒体内表面为接触面,波发生器外表面为目标面,柔轮转矩为30 N·m。

3 有限元分析

3.1 柔轮筒底圆弧半径的影响

对于筒形柔轮而言,轴向长度越短,齿圈部位的最大应力值越大,应力集中现象就越显著,也就越容易发生失效。在结构改进后柔轮中,长径比远远大于长筒形柔轮,最大应力值却没有增大,反而有大幅度减小。在其它参数不变的前提下,笔者对筒底圆弧半径r3的分析范围为2～3 mm,长筒形柔轮与结构改进后柔轮应力云图对比如图6所示。由图6可知,长筒形柔轮的最大应力值为588.06 MPa,最大应力位于齿圈与筒身的连接处;筒底圆弧半径r3为2.1 mm时,结构改进后柔轮的最大应力值为624.13 MPa;筒底圆弧半径r3为2.5 mm时,结构改进后柔轮最大应力值为501.55 MPa。结构改进后,柔轮齿圈与筒身连接处的应力集中得到改善,筒底应力位置转移至双圆弧结构。

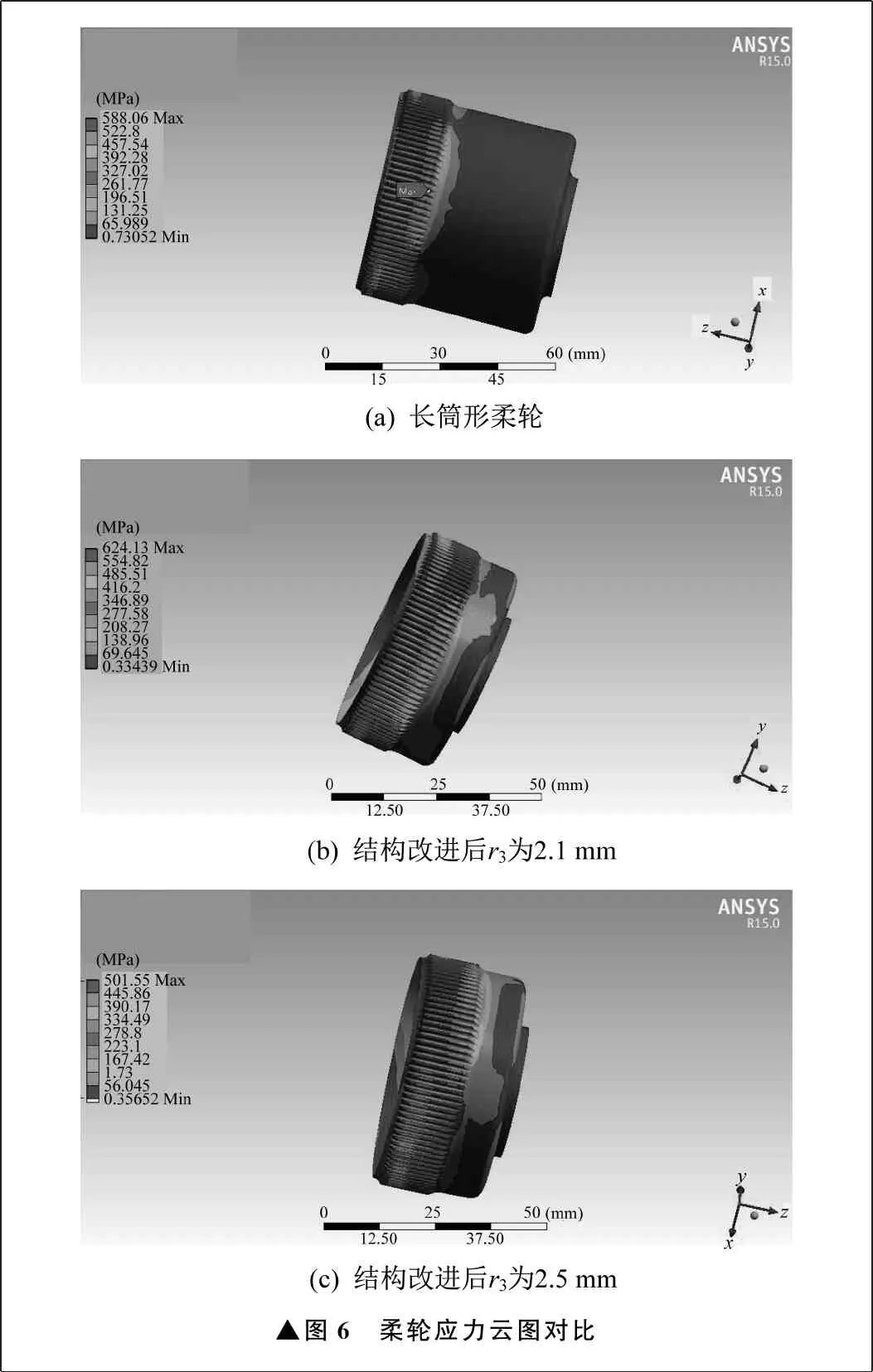
▲图6 柔轮应力云图对比

结构改进后不同筒底圆弧半径r3时的柔轮最大应力值见表2。

由表2可以看出,当r3为2.0 mm时,结构改进后柔轮的最大应力值与长筒形柔轮最大应力值相差不大;当r3为2.1 mm时,结构改进后柔轮的最大应力值达到最大值;当r3为2.5 mm时,结构改进后柔轮的最大应力值出现极小点,为长筒形柔轮最大应力值的85%;r3大于2.5 mm后,结构改进后柔轮的最大应力值缓慢增大。由此可见,柔轮筒身长度缩短了46%,最大应力值减小了15%左右。

表2 结构改进后不同筒底圆弧半径时柔轮最大应力值

3.2 柔轮壁厚的影响

长筒形柔轮的壁厚T为0.4 mm,对于结构改进后柔轮,令其它参数不变,壁厚T的分析范围为0.3～0.5 mm。不同壁厚下结构改进后柔轮的应力云图如图7所示。由图7可知,壁厚T为0.3 mm时,结构改进后柔轮的最大应力值为533.86 MPa;壁厚T为0.4 mm时,结构改进后柔轮的最大应力值为501.55 MPa,最大应力位于柔轮齿圈与筒身连接处;壁厚T为0.5 mm时,结构改进后柔轮的最大应力值为544.29 MPa。

▲图7 不同壁厚下结构改进后柔轮应力云图

结构改进后不同壁厚T时的柔轮最大应力值见表3。当T在0.3～0.35 mm之间时,结构改进后柔轮的最大应力值由533.86 MPa急剧减小至485.54 MPa。当T在0.35～0.5 mm之间时,结构改进后柔轮的最大应力值由485.54 MPa急速增大至544.29 MPa。当T为0.35 mm时,结构改进后柔轮的最大应力值出现极小点。

表3 结构改进后不同壁厚时柔轮最大应力值

3.3 柔轮齿宽的影响

设壁厚T为0.4 mm,筒底圆弧半径r3为2.5 mm,其余参数不变,齿圈宽度b取值范围为10～14 mm,不同齿圈宽度下结构改进后柔轮的应力云图如图8所示。由图8可知,当齿圈宽度b为10 mm时,结构改进后柔轮的最大应力值为561.54 MPa;当齿圈宽度b为12 mm时,结构改进后柔轮的最大应力值为499.28 MPa;当齿圈宽度b为14 mm时,结构改进后柔轮的最大应力值为552.14 MPa。虽然齿圈宽度对结构改进后柔轮应力的影响较小,但是齿圈宽度不能太大。当齿圈宽度大于12 mm时,结构改进后柔轮的应力迅速增大,从499.28 MPa增大至552.14 MPa。

4 结束语

笔者以某型谐波减速器为例,应用有限元软件分析了不同柔轮结构对柔轮应力的影响,并根据分析结果对长筒形柔轮结构进行大胆改进,将原有的直角筒壁改为双圆弧形式。结构改进后缩短了柔轮轴向长度,分析了不同结构参数下柔轮最大应力的变化规律,选择最佳结构参数进行设计,使柔轮的最大应力值减小了10%～20%,并使柔轮的整体应力位置发生变化。长筒形柔轮最大应力出现在齿圈齿根部位,结构改进后柔轮最大应力位置向双圆弧处偏移。柔轮齿圈的应力大幅度减小,提高了柔轮轮齿与刚轮轮齿的啮合效率,进而提高了谐波减速器的整体性能。

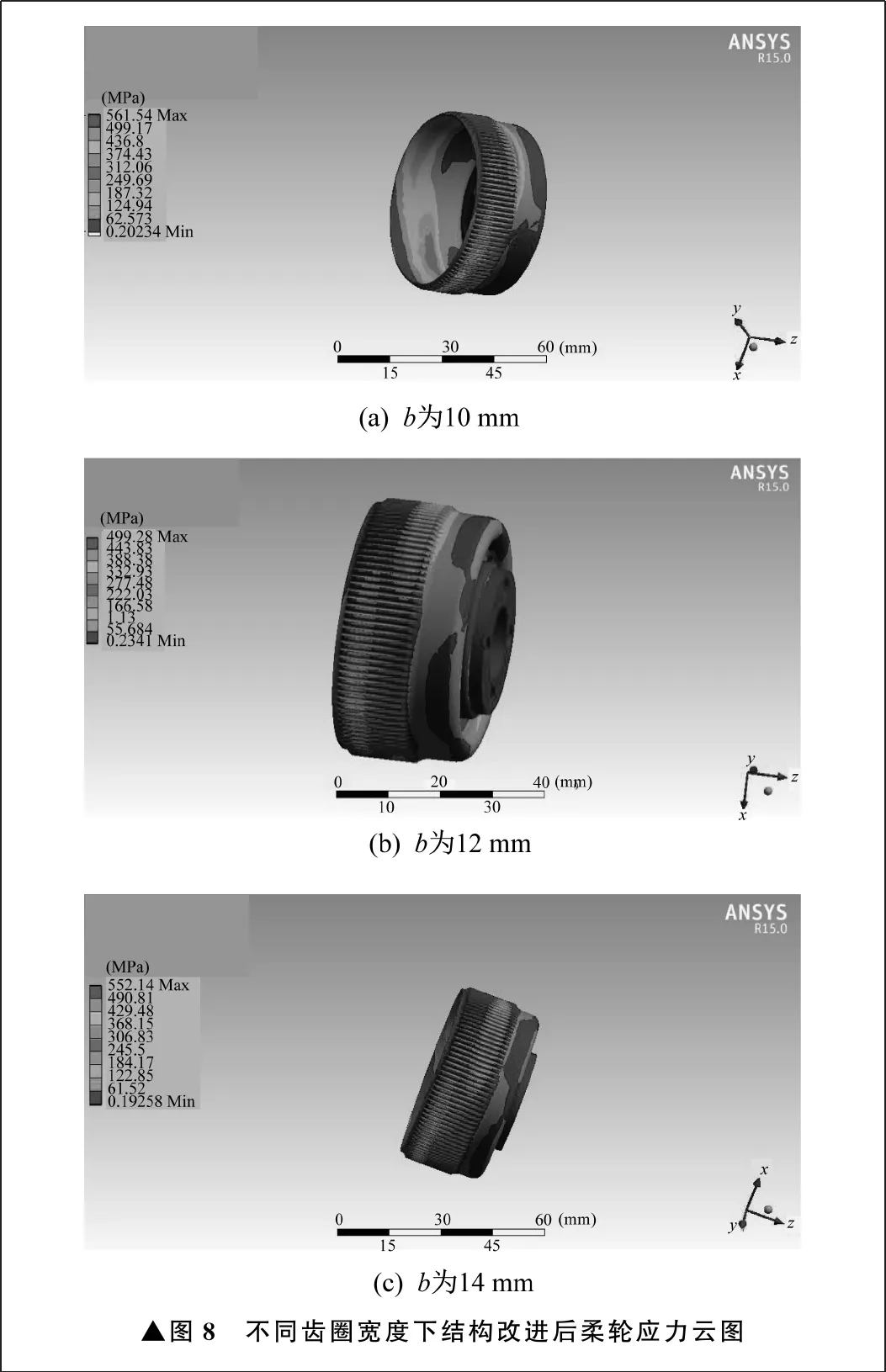
▲图8 不同齿圈宽度下结构改进后柔轮应力云图