给定悬挂点数和关联Q-谱半径最大的k一致超图的结构
2021-12-17朱忠熏周鋆鹏
朱忠熏,周鋆鹏
(中南民族大学 数学与统计学学院,武汉 430074)
矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中,但随着社会的发展,高阶高维、多索引数据在科学和工程领域的应用变得十分广泛.因此作为矩阵的高阶推广,张量(超矩阵)开始被学者们所关注.由于张量与超图有着自然的对应关系,因此可用张量来研究超图.当今,超图理论已经成为了相关领域学者们研究的热点问题.很多关于超图谱理论的结果和性质被提出,关于一致超图的结果可看文献[1-4];关于一般超图的结果可看文献[5-6];关于超图极谱的结果可看文献[7].文献[2]中作者首次提出了关联张量的概念,通过该张量的元素可以得到在与该张量对应的一致超图中包含某一个、两个、或两个以上点的超边数量,该性质是其他张量所不具有的,因此本文致力于研究关联张量.在文献[2]中给出了一般超图对应关联张量的一些重要性质;并且刻画了一致超树的极值结构.本文则刻画阶数为n且具有r个悬挂点的k一致连通超图的极值结构,刻画了n-r≥k,以及n-r∈[k-1]中的一些情况.
1 准备知识

对于正整数k,张量A=(Ai1i2…ik是一个k阶n维的数组,其ij∈[n]:={1,…,n},j∈[k].如果对于下标的任意置换σ有Ai1i2…lk=Aσ(i1)σ(i2)…σ(ik),则称张量A是对称的.
对阶数为n大小为m的k一致超图H,它的关联矩阵B(H)定义为B(H)=(B(H)ij)n×m,其中:
H的关联张量定义为Q*(H)=B(H)IB(H)T(见文献[8]),这里I是适当维数的单位张量.通过张量积的定义[9],有:
(Q*(H))i1i2…ik=(B(H)IB(H)T)i1i2…ik=
对边e={vi1,…,vik}和向量x∈Rn,记x(e)=xvi1+…+xvik,则:
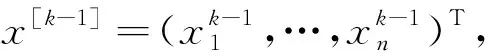
ρ(Q*(H))=max{|λ|∶Q*(H)xk-1=λx[k-1]}.
通过著名的Perron-Frobenius定理,存在一个对应于ρ(Q*(H))的单位正向量,称其为H的主特征向量.为了方便,记ρQ(H)=ρ(Q*(H)).
引理1设H是连通k一致超图.若H′是H的子图,则ρQ(H′)≤ρQ(H).
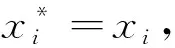
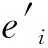
引理3设H=(V,E)是连通k一致超图且x是H的主特征向量.对i,m∈V(H),如对每一条边e∈E,i∈e暗示着m∈e,则xi≤xm.此外,如存在一条边包含点m且不包含i,则xi 则: 通过引理2和引理3,类似于文献[10]中引理5的证明,有下面的结果. (i)c=2且t=0,或c≥3(参见文献[10]). 结论1F(V1)⊇F(V2)⊇……⊇F(Vc). 对任l2>l1,l1,l2∈[c],如果存在点u∈F(Vl2)F(Vl1)和点v∈F(Vl1)F(Vl2),使得xu≥xv.设H1=H+((el1{v}∪{u})-el1,则通过引理2得ρQ(H1)>ρQ(H),矛盾.因此F(Vl2)⊆F(Vl1)或F(Vl1)⊆F(Vl2).注意到|F(Vl2)|=k-|Vl2|≤k-|Vl1|=|F(Vl1)|.故F(Vl2)⊆F(Vl1).由l1,l2的任意性可得结论1. 设 因|V0|+|F(V1)|=n-r≥k+1且|V1|+|F(V1)|=k,有|V0|>|V1|.通过引理3,可设: 因|Vi+1|>|Vi|,设 ρQ(H)+[x(e0)]k>ρQ(H). 这与H具有最大关联Q-谱半径相矛盾,因此 结论3|V1|=|V2|=…=|Vc|. 得到一个矛盾.则|Vc|≤|V1|.注意到 1≤|V1|≤|V2|≤…≤|Vc|,因此 |Vc|=|V1|且|V1|=|V2|=……=|Vc|. 如果|V1|≥2,设H3是由H通过删除e1并且添加|V1|条边生成的超图,这里每条新边包含V1中的一个点,V0中的任|V1|-1个点和F(V1),容易看出: 结论4设u∈Vi,i∈[c]且v∈e0,则xu H6=H-ei+{{ei{uk}}∪{uj}}. 对于连通k一致超图,首先得出了n-r≥k+1时,具有最大关联Q-谱半径的唯一超图;又得出了n-r=k时,具有最大关联Q-谱半径的唯一超图;最后考虑了n-r≤k-1中的r=c(k-n+r)和r=c(k-n+r)+1两种情况,分别得出了具有最大关联Q-谱半径的唯一超图.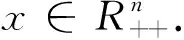
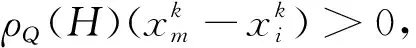
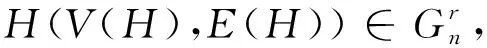
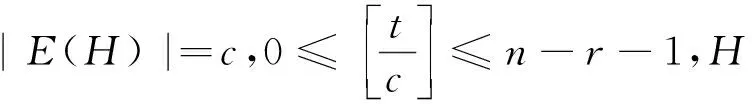
2 主要结果

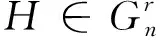

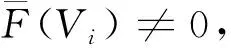
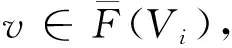


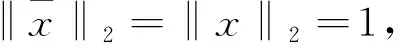
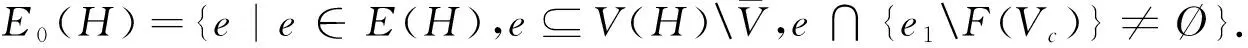


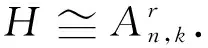
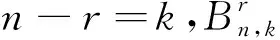
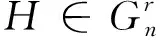


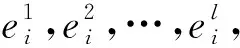

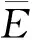


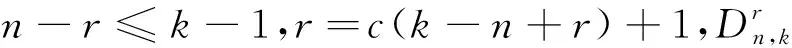

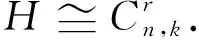


3 结论
