任意面内荷载作用下薄圆盘的自由振动与屈曲分析

李国荣 周叮 李雪红 霍瑞丽

摘要： 基于单集中力作用下半无限平面的应力分布公式，利用外载荷叠加原理，得到自平衡面内集中力系作用下薄圆盘的应力分布公式，通过积分计算进一步获得自平衡面内分布力系作用下薄圆盘的应力分布表达式。取切比雪夫多项式与边界函数的乘积作为容许函数，应用里兹法分别导出薄圆盘在任意面内静力荷载作用下的横向自由振动与屈曲的特征值方程，数值求解特征值方程得固有频率和屈曲荷载。与取幂级数和傅里叶级数乘积作为容许函数以及有限元结果对比验证了方法的快速收敛性和高精度。

关键词： 横向振动; 屈曲; 薄圆盘; 面内荷载; 里兹法

中图分类号： O326; TU311.3 文献标志码： A 文章编号： 1004-4523（2021）05-1001-08

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.014

引 言

薄壁结构具有重量轻、经济性好等优点，被广泛应用于航空、桥梁、机械等领域，在使用过程中人们发现其较易发生共振。而结构边界约束等亦会引起薄壁结构的面内初应力，导致其原有的动力特性发生改变，使得实际使用中出现的共振难以控制。

圆盘在经典边界条件下的振动研究已十分成熟，一些学者研究了圆盘在各种边界条件下的振动特性。石先杰等[1]采用谱几何法分析了弹性边界条件下圆盘横向自由振动特性。武兰河等[2]采用微分容积法求解任意边界条件下中厚圆盘的轴对称自由振动。李秋红等[3]采用改进的Fourier?Bessel级数方法和Rayleigh?Ritz法对任意弹性边界条件下圆盘的自由振动进行分析。Shi等[4]提出了一种求解任意边界条件下圆盘自由振动的统一方法，将位移解用一种简单的三角级数展开形式表示。Zhang等[5]基于简化板理论和改进的二维傅里叶?里兹法，建立了圆盘在各种弹性边界条件下振动特性的统一分析模型。对于面内荷载作用下的振动特性也有学者进行了研究，杜国君[6]分析了均布载荷作用下圆盘在非线性弯曲静平衡构形附近的微幅自由振动，使用修正迭代法求解，得到了固有频率?载荷的特征关系。Maretic等[7]以贝塞尔函数形式给出了等压作用下圆盘横向振动的解析解。上述研究表明：初始荷载显著影响结构的动力学性能，而固有频率是反映结构力学特性的一个重要参数。

关于薄圆盘的屈曲问题，早在19世纪末，Bryan[8]就指出：沿周边受压圆盘的屈曲荷载与径向对称屈曲模态相对应。而对于复杂荷载作用下薄圆盘的屈曲问题，此时的挠度将不再是径向对称，求其解析解是十分困难的，这方面的研究文章还不多见。Aung等[9]研究了薄圆盘在中间和边缘径向载荷作用下的弹性屈曲问题。马连生等[10]根据圆盘轴对称特征值问题数学上的相似性，研究了不同理论间圆盘特征值的解析关系。邱文彪[11]利用圆盘的应变能构造圆盘屈曲问题的哈密顿体系，将圆盘临界载荷和对应屈曲模态的求解归结为广义辛本征值和辛本征解问题。丁华建等[12]利用有限元软件计算了圆盘在不同计算单元模式下的屈曲问题，结果表明，常用的板和壳单元对薄板屈曲问题求解有一定的局限性。Ayoub等[13]研究了圆盘在一对径向集中力作用下的自由振动与屈曲特性。张海军等[14]使用Ritz法求解了薄圆盘在径向面内荷载下的振动和屈曲特性。

本文基于弹性力学基本公式，引入参数h为力的作用线到圆心的距离，推导出圆盘在任意自平衡面内荷载作用下的应力场解析解。将应力场方程代入圆盘能量方程，得到任意面内荷载下振动与屈曲的特征方程，采用切比雪夫多项式和边界函数的乘积作为位移试函数，通过求解特征方程可以对任意面内荷载作用下圆盘的振动与屈曲特性进行分析。研究结果弥补了分析初应力下圆盘动力特性及稳定性时，面内载荷只能为径向加载的不足。

1 任意自平衡面內荷载作用下薄圆盘的应力场

1.1 自平衡集中力系作用下圆盘的应力场

考察半无限空间中如图1所示的薄圆盘区域，集中力P沿弦AB方向作用于A点，设其力的作用线AB至圆心O的距离为弦心距h，与r轴的夹角为。

由集中力作用下半无限平面应力公式可知[15]，在集中力P作用下，点M处沿r2方向的应力为

为维持与集中力P的平衡，沿圆盘边界需存在合力指向A点的分布载荷。当存在多个集中力时，每个集中力都会在圆盘边界引起对应的分布荷载。当圆盘边界的集中力自平衡时，则边界载荷径向均布，满足

把圆盘从半空间取出，将式（2）反向施加于圆盘边界即可满足边界处分布荷载为0。因此，自平衡集中荷载作用下圆盘内任一点的应力为式（1）与（2）的反向叠加。

过圆心O点做CD与力P作用线平行，将点M沿r2的应力转化为以点O为原点，r为正方向的极坐标应力：

1.2 自平衡分布力系作用下圆盘的应力场

如图2所示，假设一个面内分布力函数表达式为，其中为分布力的最大值。那么作用于位置的力为，则对于范围内的作用力可以看作是集中力，其值为。将代入式（6）?（8）并在区间[，]，[，]进行积分，可得K个分布力系作用下的圆盘面内应力：

1.3 任意自平衡荷载作用下圆盘的应力场

任意面内力系是指由分布荷载（I个）与集中力（K个）共同作用的面内力系。根据线性叠加原理，多个力的共同作用效应，可以分解为各个力分别作用下效应的代数和。根据该原理，由1.1节和1.2节的解可推导出任意面内力系作用下圆盘的面内应力为

2 振动与屈曲方程

2.1 振动方程

在弹性力学中，薄圆盘在极坐标下经过无量纲化的最大变形能Umax、最大外力功Wmax、和最大动能Tmax分别为：

式中 为圆盘的弯曲刚度，为振型函数，为Laplace算子，为密度，为圆盘厚度，为圆盘半径，为泊松比，为固有振动频率，，和为前面求得的圆盘无量纲径向应力、环向应力和切向应力。

采用分离变量法构建圆盘的振型函数，在径向使用第一类切比雪夫多项式，表示振型[16]，在环向使用傅里叶级数表示振型

求解特征方程（20），可得圆盘在面内荷载作用下的无量纲频率。

2.2 屈曲方程

由板的稳定性理论可知，当时，对应的荷载为圆盘的最小屈曲荷载，则式（20）可退化为

3 收敛性与精确性分析

为了验证本文方法的收敛性，分别考查如图3?4所示周边简支薄圆盘在两对平行集中力作用下的固有频率值和一对局部分布荷载作下的屈曲值，荷载参数如表1所示。圆盘半径R=1 m，厚度H=0.015 m，弹性模量E=210 GPa，密度ρ=7800 kg/m3，泊松比μ=0.3。表2给出了简支圆盘无量纲固有频率的收敛性，表3给出了简支圆盘无量纲屈曲值的收敛性。对式（20）和（21）求积分时，采用分段Gauss求积法，将圆盘域沿径向等分为10个区间，环向等分为24个区间，每个区间采用15个Gauss点计算。可以看出，当截断级数取M=N=8时，可精确到三位有效数字，在后续的计算中均采用与此例相同的分段和级数项。利用ABAQUS有限元软件进行计算，使用三角形自由映射法将圆盘划分为257061个单元，采用S3壳单元进行计算。将得到的结果与本文对比，可以看出，本文结果与有限元结果十分吻合，最大误差仅为0.94%。图5给出了图3加载方式所对应的前3阶振型模态。

下面分别考察简支圆盘的无量纲频率、周边均布荷载作用下的无量纲屈曲荷载和一对径向集中力作用下的无量纲屈曲荷载，将本文解与文献[13?14]及有限元结果比较，如表4，5和6所示。

表4中，文献[13]遗漏了二阶频率，其余数值与本文吻合良好。表5中，本文解与FEM解基本一致，但与文献[14]的三、四阶频率差异很大。表6中，本文解与FEM 吻合较好，高阶频率精度优于文献[14]。

在表3中本文给出了一对极小范围内分布荷载作用下的简支圆盘屈曲值，如将其近似为集中荷载，则对应的屈曲荷载为pcr1=3267.613×0.004=13.046，与集中荷载作用下的屈曲值13.161比较，误差仅为0.87%，也间接证明了本文方法的精确性。

4 参数分析

4.1 集中荷载位置对圆盘屈曲载荷的影响

考虑如图3所示受两对平行荷载作用简支圆盘的无量纲屈曲荷载，分析载荷位置的影响，集中力位置变化范围h=[0， R/2]。图6给出了前6阶求解结果，可以看出，在h由0增大到R/2的过程中，h=R/6之前，圆盘的屈曲荷載变化均较为平缓，而在h=R/6之后则呈增大趋势，尤其是高阶屈曲值增幅明显。圆盘的一阶屈曲荷载在h=R/6附近达到最低点，说明于此处加载集中力，圆盘最易发生屈曲。此外，在h=0时所得到的前6阶屈曲荷载，为表6中一对径向集中荷载作用下简支圆盘屈曲载荷的一半，再次证明了本文方法的正确性。

4.2 集中荷载大小和位置对圆盘固有频率的影响

考察如图3所示受两对平行集中力作用的简支圆盘，集中力变化范围为[-Pcr1，Pcr1]，负值代表圆盘承受拉力，加载位置h=0.5R。图7给出了前6阶无量纲频率。

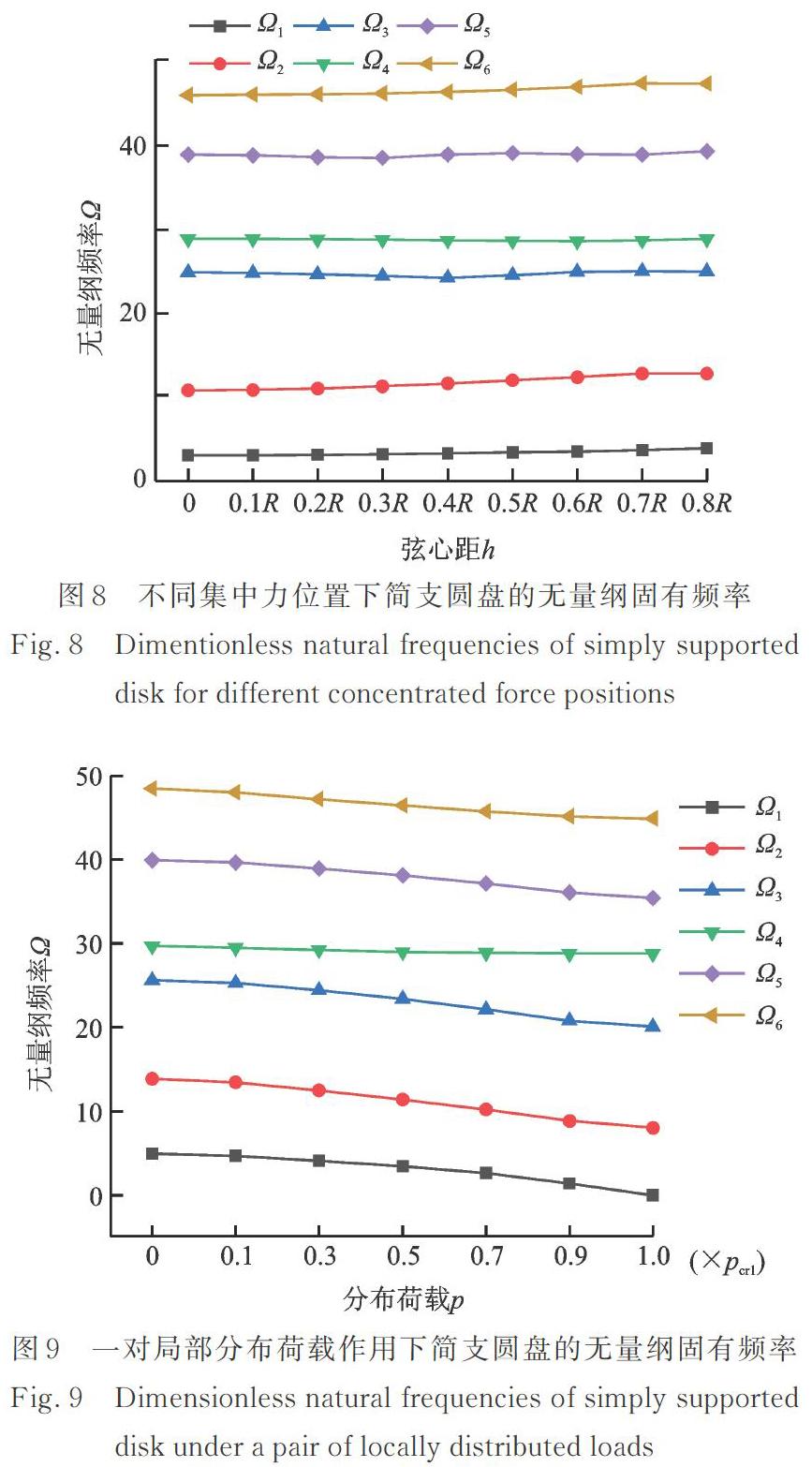
分析两对平行荷载作用位置对简支圆盘固有频率的影响，集中力值为260000 N，作用位置的范围h=[0， 0.8R]。图8给出了前6阶无量纲固有频率。

图7和8显示，集中力位置变化对圆盘固有频率的影响不明显，但集中力大小对圆盘固有频率的影响较为显著，压缩集中力增大使得圆盘的固有频率降低，而拉伸集中力增大导致固有频率升高。

4.3 分布荷载大小对圆盘固有频率的影响

考虑图4所示分布荷载大小对圆盘无量纲固有频率的影响，分布荷载大小变化范围为[0， pcr1]，h为[-0.002R， 0.002R]，图9给出了圆盘的前6阶无量纲频率随分布荷载大小的变化，可看出，随外荷载增大圆盘的各阶固有纲频率都减小，且当分布荷载增大到一阶屈曲荷载时，圆盘的一阶固有频率降为0。

4.4 分布荷载范围对圆盘屈曲载荷的影响

研究如图10所示受自平衡集中力P1与分布荷载p2共同作用下简支圆盘的屈曲载荷，P1为径向集中力，p2为关于r轴对称的均布荷载，方向沿r轴。h的变化范围为[0.002R， 0.5R]，结果如图11所示。可以看出，无量纲屈曲荷载随分布荷载范围的扩大而增大，阶数越高增幅越大。

5 结 论

本文研究了任意自平衡面内荷载作用下薄圆盘的振动与屈曲特性。首先推导了圆盘在面内荷载作用下应力场的解析解，然后使用Ritz法建立能量方程，选取切比雪夫多项式做容许函数，求解了圆盘在任意面内力作用下的无量纲固有频率和屈曲载荷。讨论了两对平行集中力作用下，荷载大小和加载位置对圆盘固有频率及屈曲载荷的影响和分布荷载作用下，荷载大小对圆盘频率的影响，以及分布荷载与集中力共同作用下分布荷载范围对圆盘屈曲载荷的影响，主要结论如下：

（1）获得了任意自平衡载荷作用下圆板面内应力分布的解析解，扩大了解析法的求解范围。

（2）使用切比雪夫多项式和边界函数的积作为容许函数求解圆盘的振动与屈曲特性优势明显。与文献[13?14]及有限元对比证明了方法的高精度。与有限元需划分网格相比计算量小，且参数化分析比有限元简单得多。

（3）简支圆盘在承受两对平行集中力时，集中力作用位置在R/6附近最易发生屈曲，而集中力位置对频率的影响较小。简支圆盘在承受一个集中力与一个分布荷载时，荷载分布范围对圆盘高阶屈曲载荷值的影响大于低阶。

（4）本文提供的方法能计算任意面内自平衡荷载作用下圆盘的固有频率与屈曲载荷。消除了分析圆盘自由振动与屈曲时面内荷载必须过圆心的限制，完善了圆盘在各种面内荷载作用下的自由振动与屈曲特性研究。

参考文献：

[1] 石先杰， 李春丽， 蒋华兵， 等. 弹性边界条件下圆板横向自由振动特性分析[J]. 振动.测试与诊断， 2016， 36（5）：984-989.

SHI Xianjie， LI Chunli， JIANG Huabing， et al. Analysis of transverse free vibration characteristics of circular plate under elastic boundary condition [J]. Journal of Vibration， Measurement & Diagnosis， 2016， 36（5）： 984-989.

[2] 武兰河， 李向国， 王立彬. 圆板轴对称自由振动的微分容积解法[J]. 振动与冲击， 2003， 22（3）：75-77.

WU Lanhe， LI Xiangguo， WANG Libin. Differential cubature method for solving axisymmetric free vibration of thick circular plates[J]. Journal of Vibration and Shock， 2003， 22（3）：75-77.

[3] 李秋红， 刘广明， 薛 开， 等. 圆形薄板在任意弹性边界条件下的自由振动分析[J]. 船舶力学， 2015，（Z1）：162-168.

LI Qiuhong， LIU Guangming， XUE Kai， et al. Free vibration analysis of circular plates with general elastic boundary support[J]. Journal of Ship Mechanics， 2015，（Z1）：162-168.

[4] Shi X， Shi D， Li W L， et al. A unified method for free vibration analysis of circular， annular and sector plates with arbitrary boundary conditions[J]. Journal of Vibration and Control， 2016， 22（2）： 442-456.

[5] Zhang H， Zhu R， Shi D， et al. A simplified plate theory for vibration analysis of composite laminated sector， annular and circular plate[J]. Thin-Walled Structures， 2019， 143： 106252.

[6] 杜国君. 均布载荷作用下圆薄板的自由振动[J]. 振动与冲击， 1996，（2）：33-37.

DU Guojun. Free vibration of circular plate under uniform load[J]. Journal of Vibration and Shock， 1996，（2）：33-37.

[7] Maretic R， Glavardanov V. Vibration of circular plate with an internal elastic ring support under exterior edge pressure[J]. International Journal of Structural Stability and Dynamics， 2014， 14（1）： 1350053.

[8] Bryan G H. Buckling of plates[J]. Proceedings of the London Mathematical Society， 1891：22-54.

[9] Aung T M， Wang C M. Buckling of circular plates under intermediate and edge radial loads[J]. Thin-Walled Structures， 2005， 43（12）：1926-1933.

[10] 馬连生， 王铁军. 不同理论下圆板特征值之间的解析关系[J]. 应用数学和力学， 2006， 27（3）：253-259.

MA Liansheng， WANG Tiejun. Analytical relations between the eigenvalues of circular plate based on various plate theories[J]. Applied Mathematics and Mechanics， 2006， 27（3）：253-259.

[11] 邱文彪. 圆板屈曲问题中的哈密顿体系方法[D]. 大连： 大连理工大学， 2014.

QIU Wenbiao. A Hamiltonian system method for buckling problem of thin circular plates[D]. Dalian： Dalian University of Technology， 2014.

[12] 丁华建，蒋 泉.对圆薄板屈曲响应有限元分析的研究[J].南通大学学报（自然科学版）， 2006，5（4）：29-31.

DING Jianhua， JIANG Quan. Analysis of finite element about the buckling problem of circular thin plate[J]. Journal of Nantong University （Natural Science）， 2006，5（4）：29-31.

[13] Ayoub E F， Leissa A W. Free vibration and tension buckling of circular plates with diametral point forces[J]. Journal of Applied Mechanics， 1990， 57（4）： 995-999.

[14] 张海军. 任意面内荷载作用下圆板的弯曲、振动与屈曲分析[D]. 南京： 南京理工大学， 2004.

ZHANG Haijun. Vibration and buckling analysis of circular plate under arbitrary surface load [D]. Nanjing： Nanjing University of Science and Technology， 2004.

[15] 铁摩辛柯， 古地尔. 弹性理论[M]. 徐芝纶， 译. 第3版. 北京： 高等教育出版社， 2013： 86-88.

Timoshenko S P， Goodier J N. Theory of Elasticity [M]. 3rd ed. Beijing： Higher Education Press， 2013： 86-88.

[16] 何福保， 沈亚鹏. 板壳理论[M]. 西安：西安交通大学出版社， 1993： 64-65.

HE Fubao， SHEN Yapeng. Plate and Shell Theory[M]. Xi'an： Xi'an Jiaotong University Press， 1993： 64-65.

作者简介： 李国荣（1992-）， 男， 硕士研究生。电话： 18351888151; E-mail： 18351888151@163.com

通讯作者： 霍瑞丽（1980-）， 女， 副教授， 硕士生导师。电话： （025）58139521; E-mail： ruilihuo@njtech.edu.cn