方形截面高层建筑风致振动特性的数值模拟
2021-12-16卢姗姗张志富陈文礼
卢姗姗 张志富 陈文礼

摘要: 以宽高比1∶6的方形截面高层结构为研究对象,利用计算流体软件FLUENT,基于雷诺应力模型RSM求解不可压缩黏性流体的Navier?Stoke方程,结构的振动响应通过Newmark?β方法(通过用户自定义函数UDF与软件连接)求解,以此来研究该结构的风致振动特性,同时获得刚性静止模型与气动弹性模型在均匀风速流场与不同指數率风剖面下的绕流场规律。数值模拟结果表明:高层建筑结构存在着明显的涡激振动风速锁定现象,振动位移和锁定区宽度与风洞试验结果接近;在风剖面流场作用下,位移响应的变化规律与流场的平均风速有关,当平均风速接近锁定区域时,结构的位移响应最大;随着梯度风速的增加,结构分别呈现1阶和2阶风致涡激振动。高层建筑结构绕流场具有显著的三维特征,沿着高层建筑高度的方向,旋涡发展是不平衡的,越接近结构底部的绕流场,呈非对称性的旋涡脱落,而越靠近顶部的尾流场,呈对称性的旋涡脱落,且其递变的规律与流场速度分布有关。
关键词: 高层建筑; 涡激振动; 流固耦合; 数值模拟; 绕流场
中图分类号: TU973.2+13; TU352.1 文献标志码: 文章编号: 1004-4523(2021)05-0911-11
DOI:10.16385/j.cnki.issn.1004-4523.2021.05.004
引 言
随着工业技术的不断发展,越来越多的高层建筑乃至超高层建筑迅速涌现。高层建筑作为一种高度高,刚度小的细长型结构,在大多数时候,风荷载是它的控制荷载。在高层建筑的发展过程中,伴随着高强轻质材料的广泛运用和新型结构体系的出现,现代城市的建筑高度越来越高,阻尼比越来越小,高层建筑更轻更柔,使其固有频率越来越接近自然风的卓越频率,对风荷载的敏感性越来越强。
引起高层建筑的风致振动响应主要包括来流风脉动引起的抖振和旋涡脱落引起的涡振。抖振是由于大气边界层的湍流脉动引起的,是一种顺风向振动响应。一般来说,低、中层建筑刚度较大,而高层结构乃至超高层结构的柔度大,固有频率低,很有可能处在阵风的频率范围内,因此,高层建筑更容易受到抖振的影响。而涡振易发生于许多钝体绕流中,当旋涡脱落频率(由斯托拉哈数确定)接近建筑物的固有频率时,建筑固有频率控制旋涡脱落频率,这种现象称为“锁定”。旋涡的周期性交替脱落成为影响柔性结构安全性、耐久性的一个重要问题。
早在20世纪70年代就已经开展了对高层建筑的横风向气动力的研究,如Saunders等[1]比较不同建筑高宽比、来流风场湍流度和折减风速识别出了横风向气动力谱,并比较了不同因素对横风向气动力谱的影响。在20世纪80年代的后期,Islam等[2]和Kareem[3]分别利用刚性模型风洞测压试验得到,横风向响应是由两侧不均匀的脉动压力引起的,这种不均匀脉动受到剪切层分离和尾流脉动的影响。全涌等[4]基于高层建筑横风向气动力与气动阻尼,得出了高层建筑横风向风致响应及等效静力风荷载的计算方法。
对于涡激振动,众多学者也采用了各种方法去揭示其机理,为工程实际提供思路。Zhang等[5]采用LES的方法对二维圆柱的横向振动进行研究,结果证明了他们的数值模拟方法与实验相比具有很高的精确性。徐枫等[6]用基于雷诺应力模型的数值方法模拟了方柱和流场之间的流固耦合作用,用弱耦合的方法观察到了明显的“频率锁定”、“拍”和锁定段的位移失谐现象。邓见等[7]采用数值模拟的方法对方柱的振动响应进行模拟,成功捕捉到了驰振到涡致振动的转变风速,并发现涡激振动的“锁定”、“相位开关”等现象,其计算结果为实际工程提供了启示。Revuz等[8]利用大涡模拟(LES)的数值模拟方法对高层建筑在风荷载激励下的动力响应进行了模拟研究,将静止结构的数值结果与流固耦合作用下的动态响应的结果进行了比较,验证了涡激响应的“锁定”现象。许媛欣[9]研究了单自由度方柱在均匀来流下的涡激振动,分析升阻力系数、位移振幅等参数随频率比的变化情况及尾流场的模态特征,并讨论了不同质量比对涡激振动的影响。Chen等[10]用数值模拟方法模拟了斜拉索在不同的风速剖面下的横风向涡激振动,并观察到了斜拉索多模态振动呈“行波”响应,单模态振动呈“驻波”响应。
现阶段的研究主要是针对不同结构的涡激振动特性而开展的,但对于高层建筑结构在不同风场作用下呈现的风致振动特性与绕流场特征还没有进行深刻的研究,基于这一点,本文以宽高比为1∶6的方形截面的高层结构为研究对象,对高层结构的风致振动进行了数值模拟。
1 计算模型
高层建筑结构的风致振动响应是一个多模态耦合的问题,即流固耦合。本文先通过建立高层结构气动弹性模型,再利用Newmark?β方法来进行结构振动响应的计算,而流场的模拟通过基于雷诺应力模型(RSM)的Fluent 18.0进行实现。
1.1 气动弹性模型的建立
本文以宽为45 m、高为270 m,宽高比为1∶6的方形截面的高层建筑结构为原型,经过1∶500的缩尺,模型尺寸为90 mm×90 mm×540 mm。沿高度方向高层建筑模型的单位长度质量为m=2.78,第1阶频率为f1=6.46 Hz,第2阶频率为f2=40.51 Hz,第3阶频率为f3=113.48 Hz,第4阶频率为f4=222.3780 Hz,1阶阻尼比为ξ1=0.018,2阶阻尼比为ξ2=0.010。
本文建立的模型为两自由度、底端固定的高层建筑结构,两自由度分别为顺风向与横风向,主要研究横风向(即涡激振动的主要方向)的振动响应,其振动方程可以写为
式中 t为时间,z为沿高度方向的轴向坐标,为轴向坐标z处的横向力(升力),m为模型单位长度质量,本文取为2.78 kg/m,c为模型单位长度阻尼,k为模型单位长度刚度。
根据振型分解法,模型的轴向各点的横向位移可写为
式中 为广义模态坐标,为第n阶模态振型函数,H为模型的高度。
高层建筑结构经过简化,可以简化为悬臂梁。根据前4阶自振频率采用曲线拟合的方法来确定模型的振型,得到如下的振型函数
式中 为通过拟合得到的参数,如表1所示。
根据振型的正交性,将式(1)中的各个量写为广义坐标形式,则第n阶的运动方程写为
式中 为模型自振圆频率,为模型阻尼比,为广义刚度,为广义气动力。
假定模型的阻尼为瑞利阻尼,根据前2阶模态的阻尼比,可求得其他各阶阻尼比。将前4阶模态振型函数代入下式,可得质量矩阵M、刚度矩阵K、阻尼系数矩阵C。
式中 与为瑞利阻尼系数,fn为结构的自振频率。
模型和流场之间的流固耦合作用采用弱耦合方法进行模拟,模型表面的气动力通过FLUENT计算,再根据Newmark?β法计算出结构的各阶模态振动位移响应,将位移y(z,t)赋给圆柱表面各点,通过动网格技术控制模型表面移动,间接使流场边界发生变化,待网格迭代收敛后,整个流场更新完毕从而开始下一个时间步的计算,以此循环得到最终计算结果,具体计算流程如图1所示。
1.2 CFD计算模型
本文的数值模拟计算采用的是商用计算软件ANSYS FLUENT,为满足模型的计算要求,计算域取29D×16D×1.85H,计算域的边界条件定义如下:
(1)进口条件设置为“速度入口(velocity inlet)”;
(2)出口条件设置为“自由流出(outflow)”;
(3)左右两侧边界条件设置为“对称(symmetry)”;
(4)上部、下部以及模型表面边界条件设置为“固壁(wall)”;
计算域的大小以及边界条件的设置如图2所示。
计算域采用混合网格的形式划分,由三个部分组成,分别是模型边界层区域C1、边界层外范围为0.5 m×0.5 m的可动区域C2,以及静止区域C3,网格总数为2300000,近壁面网格y+≈20,网格划分方式与划分结果如图2所示。
为了适应结构振动引起的周围网格变化,本文采用FLUENT中的动网格技术进行网格更新,将弹簧光顺法和局部重构法结合使用,弹簧常数为0.1,最大限制畸变率取为0.85。采用基于RANS方法的雷诺应力模型(RSM)进行数值模拟,使用有限体积法对控制方程进行离散,用3D分离式求解器隐式算法对控制方程求解,动量、湍流动能、耗散率和雷诺应力项均采用精度较高的2阶迎风格式进行离散,速度压力耦合采用SIMPLEC算法,时间步长取为0.0005 s。
本文数值模拟中计算来流为速度入口边界条件,通过UDF编程实现在FLUENT中的输入,根据规范,平均风速剖面将采用指数律经验公式,即
式中 zb为参考高度,本文为350/Lv,Lv为模型比例尺,本文为500;z为纵向高度;Ub为参考高度的风速;α为粗糙度指数,对应于A,B,C,D四类地貌分别为0.12,0.15,0.22,0.30。
来流湍流度特征则通过湍动能k和湍流耗散率ε给出,即:
式中 U(z)为高度z的平均风速,I为湍流强度,l为湍流特征尺度。
2 高层建筑的风致振动特性
2.1 刚性静止模型的数值模拟
为了验证本文数值模拟的精度,首先进行刚性静止模型的数值模拟研究,来流采用均匀流。基于模型特征尺寸和来流风速,数值模拟在Re=22000下的条件进行,计算得到升力系数CL、阻力系数CD时程、升力和阻力的频谱图,如图3所示。
根据升力与阻力系数时程曲线图,发现升力系数均值接近0,这反映了数值模型网格良好的对称性。计算得到升力的无量纲主频Strouhal数St=0.117,略微小于二维方柱的0.125?0.14,但这与前人在三维悬臂方柱上的研究结果是吻合的,如王汉封等[11]运用大涡模拟计算得到的St数为0.105,Sattari等[12]通过风洞试验测得St数为0.100。计算得到的阻力系数的无量纲主频等于0.234,阻力系數的无量纲主频与Strouhal数精确满足2倍关系。
图4给出了竖向的时均流线图,从图中可以看出三维高层建筑结构的绕流场具有十分明显的三维特性,除了两侧交替脱落的旋涡,顶部还形成了一个十分明显的向下顺时针旋转形成的涡结构,该涡结构对两侧交替脱落的旋涡产生很大的影响,起到延缓两侧的旋涡脱落的作用,这也为本文算出的St数略小于二维方柱St数给出了合理的解释。
2.2 均匀流下气动弹性模型风致振动的数值模拟
为了研究不同均匀流风速下气弹模型对的风致振动响应,本文选取的来流风速分别为3,4,4.6,4.8,5,5.1,5.2,5.45,5.7,6.1,6.5,7 m/s,根据结构基频和特征尺寸,对应的折算风速Vr=UH/(f1D)分别为5.16,6.88,7.91,8.25,8.60,8.77,9.03,9.37,9.89,10.49,11.18,12.04。
为验证气弹模型数值模拟的准确性,本文首先开展了气弹模型风致振动的风洞试验研究,试验在哈尔滨工业大学风洞与浪槽联合实验室SMC?WT2号精细化小风洞进行,试验段高度为1.2 m,宽度为0.8 m。试验采用与数值模拟模型几何尺寸一致的高层建筑结构模型,模型骨架采用铝合金杆芯和铝合金薄板焊接而成,外衣采用3D打印机打印而成。模型的自振频率经过调节为f1=6.46 Hz,与数值模拟模型一致,阻尼比为0.0039,略低于数值模拟的阻尼比,二者的动力特性对比如表2所示。将两个加速度计(B&K 4507B)分别固定在顺风向与横风向以采集加速度信号,采集后经过积分转换为位移信号,采集频率为1000 Hz,采集时间为60 s,试验模型如图5所示。
风洞试验和数值模拟得到结构振动幅值随折算风速的变化如图6所示。数值模拟与风洞试验的结果大致吻合,数值模拟对“锁定”区域的捕捉较为准确,由于试验模型的阻尼比较数值模拟小,因此其最大幅值略大于数值模拟结果。本文所采用的数值计算模型具有较高的精度和可靠性。
根据图6涡激振动折算风速锁定区范围,可计算得到相应的风速锁定区域范围大致为(1.0?1.09)Us,Us为起振风速。根据梁枢果等[13]建议的“锁定”区域范围计算公式,计算得到“锁定”区域范围为(1?1.085)Us,本文的数值模拟结果与其建议锁定区范围十分吻合。
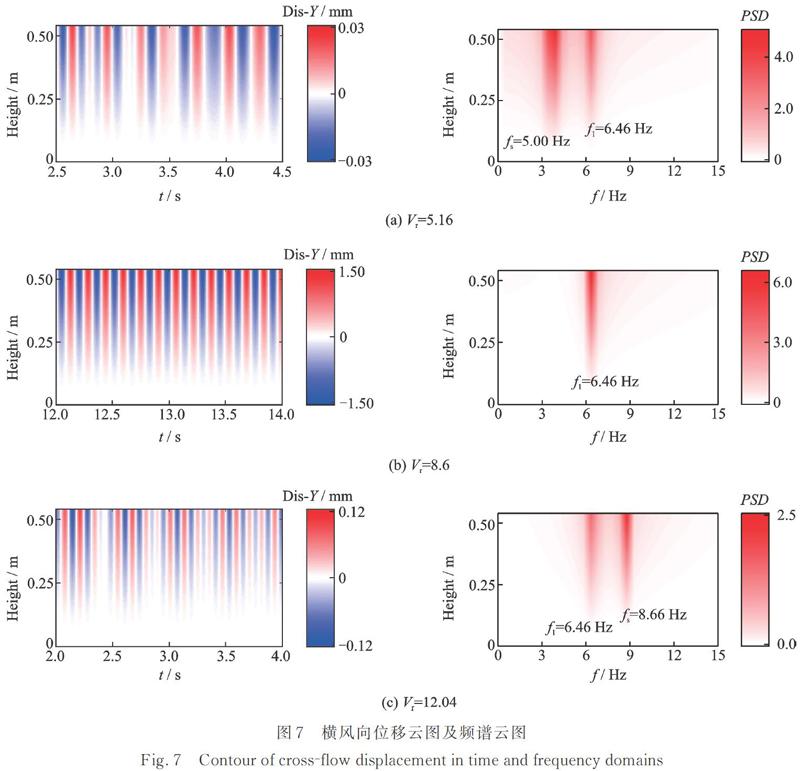
图7给出了折算风速Vr=5.16,8.6和12.04对应的结构横风向位移云图及其频谱云图,三个折算风速分别位于涡激振动锁定区前、锁定区和锁定区后。结果表明,风速在“锁定”区前,模型的位移出现正值与负值变化交替的现象,但并不是等周期变换,即呈现了“拍”现象,幅值很不稳定,如图7(a)左所示,对应的频谱图也存在着两个明显的值,其中,主动频率对应该风速下的旋涡脱落频率fs=5.00 Hz,另一个则对应于模型的基频f1=6.46 Hz,如图7(a)右所示;折算风速为8.6,对应于“锁定”区范围内,旋涡脱落频率接近模型的基频,被完全“俘获”,位移云图呈现出明显的等周期交替变换的现象,如图7(b)左所示。对应的频谱图也仅存在一个值6.46 Hz,该值等于模型的基频f1=6.46 Hz,如图7(b)右所示;而当折算风速继续增大离开“锁定”区,呈现出类似锁定区前的非等周期交替变换的现象,但与共振“锁定”区前相比,该折算风速对应的位移响应时程曲线则相对稳定了许多,如图7(c)左所示。其对应的频谱图也再次呈现了两个值,其代表的含义与共振“锁定”区前的结果类似,分别表示旋涡脱落频率fs=8.66 Hz以及基频f1=6.46 Hz,如图7(c)右所示。
2.3 风剖面下气动弹性模型的数值模拟
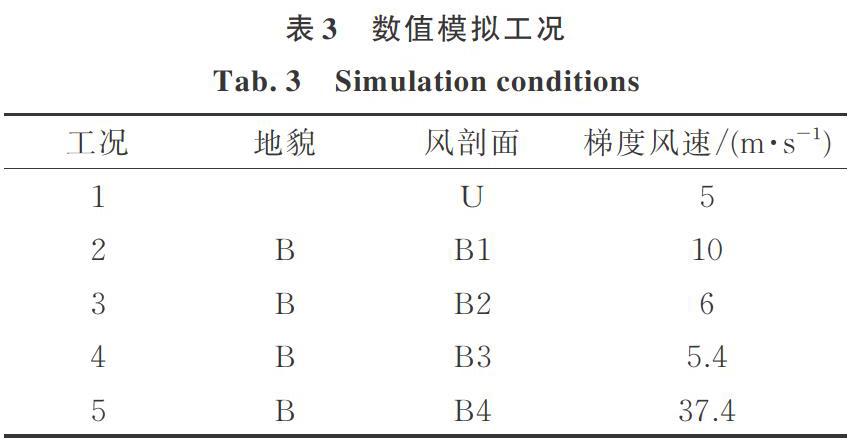
高层建筑实际上是处于大气边界层中,因此,本文进一步开展了风速剖面剪切流下的风致振動数值模拟研究。本文选取B类地貌下的风速剖面作为高层建筑的输入来流,根据式(6)?(8),通过UDF编程实现在FLUENT中速度入口风剖面的输入。为了激发结构不同阶次的涡激振动,需设置不同的来流风速剖面。根据参考高度处风速不同分为4个工况,并加入风速为5 m/s的均匀入口流场作为对照工况,如表3所示。不同工况的示意图如图8所示,其中,红色虚线标记范围为2.2节计算得到的“锁定”风速区间。B1工况锁定风速段位于结构底部,而B2和B3工况锁定风速段分别位于结构顶部和中上部,三个工况中B2的锁定风速范围最大。为了激发第2阶涡激振动,设置了B4工况。
对不同风速剖面下的高层建筑风致振动进行了数值模拟,得到的各阶振动位移响应如图9所示,图中给出了第1阶至第4阶模态的响应时程。
图9(a)结果表明,在均匀流场U的作用下,结构只产生了第1阶模态振动,第2?4阶模态振动相比第1阶均可忽略不计。根据St数的计算公式,U=5 m/s时,对应的旋涡脱落频率为6.5 Hz,与结构的1阶频率是接近的,也与理论结果吻合。
图9(b)?(e)分别是B1,B2,B3和B4工况下横风向各阶位移响应,其中B1,B2和B3工况均只产生了明显的第1阶振动响应,其余阶次位移响应均接近于0,但值得注意的是,三个工况中各阶位移时程中仍存在着明显的区别,B1与B3工况的结构振动幅值明显小于B2,主要是由涡激振动的锁定区范围不同引起,经过计算,B1工况下锁定区高度范围为0.007?0.017 m,B2工况下锁定区高度范围为0.208?0.497 m,B3工况下锁定区高度范围为0.419?0.540 m,大致分别对应于模型的下、中、上三个不同的区域。其中B1区域位于模型底部大致为0.01 m,B2区域位于模型中部大致为0.289 m,B3区域为0.121 m,在锁定区域范围最大的B2工况,产生最显著的涡激振动现象,而范围最小的B1工况则呈现出最小的位移振动响应,且由于B1工况模型梯度风速较大,更接近于第2阶模态的起振风速,因此,也产生了微弱的第2阶振动位移响应。
B4工况的梯度风速为37.4 m/s,由St数计算公式可得该风速对应旋涡脱落频率为48.62 Hz,因此,该工况旋涡脱落频率范围为0?48.62 Hz,覆盖了结构的第1和第2阶自振频率。从模态响应图中可以看到该工况存在着第1阶响应,但相比第2阶位移响应微弱很多,这是由于在该风速下,第1阶模态的锁定区域范围很小,第2阶的锁定区域范围较大,从而主导结构发生以第2阶为主的涡激振动的振动位移响应。
不同风速剖面对应的结构响应及其频谱时空分布云图如图10所示。不同的颜色代表结构响应随时间和空间的变化。结果表明,B1工况的位移各个高度处位移随着时间呈正负交替变换,但并不是等周期的变换,从频率云图中也可以看出,存在着两个明显的值,其中,主导频率为旋涡脱落频率,另一个则对应于模型的基频,因此,B1工况并未完全激发第1阶涡激振动。B3工况位移同样呈现着非周期性的变换,但是频谱中仅存在一个值,对应的是平均风速对应的旋涡脱落频率,这是因为具有与基频相同的旋涡脱落频率的锁定区范围要远小于非锁定区范围,且其锁定区位于受顶部旋涡影响最明显的区域,因此,该工况同样未完全激发第1阶涡激振动。B2工况激发了较大的位移响应,其位移云图中呈现出等周期的大幅值运动,频谱图中也仅存在于结构的第1阶自振频率接近的频率值,很明显,该工况下结构发生了显著的第1阶涡激振动。对于B4工况,可以看出其与B1?B3存在显著的区别,位移云图呈现了等周期的变换,频谱图中也仅存在着和结构的第2阶自振频率接近的频率值,相比B2工况下的涡激振动,B4工况激发了幅值很大的涡激振动,其振动幅值要大于均匀流下第1阶涡激振动的幅值,说明该结构的第2阶涡激振动幅值要大于第1阶涡激振动的幅值。
非定常升力fy (z,t)是流场作用在高层建筑结构的气动力,升力的交替变化是引起结构涡激振动的主要原因。本文通过UDF提取在高度z处的升力,并通过下式计算升力系数CL (z,t)
图11是高层建筑结构模型在U和B2工况下三个不同高度处的升力系数时程,分别是z=0.04,0.25和0.53 m。从图中可以发现,在恒定流场U的作用下,可以明显发现,不同高度的升力系数时程呈同频同步变化,且其初始相位都是相等的,但值得注意的是,不同高度处的升力系数幅值是不一样的,在靠近底部的z=0.04 m处,升力系数是最大的,而z=0.53 m处升力系数是最小的,呈现了由下到上递减的趋势,这是由于在靠近顶部位置,由于顶部旋涡结构的存在,其旋涡脱落是受到抑制的,因此顶部位置处的升力系数较小。观察B2工况的升力系数,结果表明其与U工况由上至下也呈现了同样的态势,但是升力系数均小于同样位置处的升力系数。从前文可知,B2工况中,结构仅有一部分是处于共振区域的,而U工况中整体结构均处于共振区,在B2工况中,共振区占据主动,使结构产生涡激振动,但是由于非共振区的存在,共振区需要耗费部分能量去同化非共振区,因此,其升力系数整体是偏小的。
3 高层建筑绕流场的变化规律
图4中的竖向平面的时均流线图表明高层建筑结构的绕流场具有显著的三维特性,顶部的涡结构对两侧交替脱落的旋涡产生很大的影响,该涡结构在顶部前缘分离形成下扫的旋涡,影响到了结构的大部分区域,本文依次选取z=H,H,H,H,H,H,H七个不同高度的瞬时流场结构进行分析,如图12和13所示。
图12为均匀流U工况下的各个位置的瞬时流场图,从图中可以看到,高层建筑结构由于顶部涡结构的存在,从上到下呈现了不同的流场特性,总体来说,高层建筑沿高度的方向,旋涡发展是不平衡的。在z=H时,每一个周期会产生一对方向相反的类似“卡门涡街”的旋涡,即旋涡脱落模式呈现经典的“2S”模式,而在z=H时,旋涡脱落发生明显变化,上方形成了一对相同旋转方向的旋涡对,而下方仍然是一个旋涡,这种不对称的形式,也就是“P+S”模式;在z=H和H时,下方也形成了一对同向旋转的旋涡,整个尾流场产生了两对同向旋转的旋涡,且随着高度的增加,同向旋涡对的距离增大,即形成了“2P”模式。在z=H至H,交替脱落的旋涡消失,变成了对称的旋涡对,且越靠近顶部,越具有对称性,旋涡的尺度也越小。
图13为B2与B4工况下的各个位置的瞬时流场图,可以发现,结构从下到上,涡结构也同样呈现了由“2S”,经过“P+S”模式,最后转变为“2P模式”的旋涡结构变化过程,但是在入口处添加风剖面时,对比恒定流场,前者的变化过程更加缓慢,如z=H处,U工况流场涡结构已经呈现了完整的“2P”模式,但是在B2和B4工况中,在z=H时才呈现出类似的模式,这可能是由于结构顶部的风速不同导致顶部涡结构不同。对比B2与B4工况,发现二者的涡结构沿高度的变化基本一致,但是由于B4工况整体风速显著大于B2,其涡结构也较B2工況的大。
4 结 论
本文采用CFD数值模拟研究高层建筑结构的风致振动特性与气固耦合效应,进而研究刚性静止模型与气动弹性模型在不同均匀风速流场与风剖面下的绕流场规律,得出以下结论:
(1)在共振风速附近,锁定区并不是传统的(1.0?1.3)Us范围,而是(1.0?1.09)Us。在共振“锁定”区范围内,旋涡脱落频率接近模型的固有频率,被结构频率完全“俘获”,呈现出大幅值的简谐共振响应。
(2)在风速剖面作用下,结构的振动位移响应与锁定区的位置和范围大小有关,当锁定区位置位于结构的中部并且范围足够大时,会出现明显的涡激振动。由于风速剖面作用下沿着高度的锁定区范围小于均匀流作用下的,其整体气动力以及结构响应小于均匀流作用下的结果。
(3)高层建筑结构尾流场具有显著的三维效应,顶部涡结构的存在延缓了两侧的旋涡脱落。沿着高层建筑高度的方向,旋涡发展是不平衡的,接近底部,呈非对称性的旋涡脱落,而靠近顶部,呈对称性的旋涡脱落,在非对称性的旋涡脱落区域中,随着高度的增加,旋涡脱落模式由“2S”,经过“P+S”模式,转变为“2P模式”。
参考文献:
[1] Saunders J W, Melbourne W H. Buffeting effects of upstream buildings?[J]. Wind Engineering, 1980, 1:593-606.
[2] Islam S M,Ellingwood B, Corotis R B. Dynamic response of tall buildings to stochastic wind loads[J]. Journal of Structural Engineering,1990,116(11):2982-3002.
[3] Kareem A. Dynamic response of high-rise buildings to stochastic wind loads[J]. Journal of Wind Engineering & Industrial Aerodynamics,1992,42(1-3):1101-1112.
[4] 全 涌,顾 明. 高层建筑横风向风致响应及等效静力风荷载的分析方法[J].工程力学,2006,23(9):84-88.
Quan Yong,GU Ming. Analytical method of across-wind response and equivalent static wind loads of high-rise buildings[J]. Engineering Mechanics,2006,23(9): 84-88.
[5] Zhang J,Dalton C. Interactions of vortex-induced vibrations of a circular cylinder and a steady approach flow at a Reynolds number of 13000[J]. Computers & Fluids, 1996,25(3):283-294.
[6] 徐 枫,欧进萍,方柱非定常绕流与涡激振动的数值模拟[J]. 东南大学学报(自然科学版),2005,35(S1):35-39.
Xu Feng, Ou Jinping. Numerical simulation of unsteady flow around square cylinder and vortex-induced vibration [J]. Journal of Southeast University(Natural Science Edition), 2005,35(S1): 35-39.
[7] 邓 见, 任安禄, 邹建锋.方柱绕流横向驰振及涡致振动数值模拟[J]. 浙江大学学报(工学版), 2005,39(4):595-599.
Deng Jian,Ren Anlu,Zou Jianfeng. Numerical study of transverse galloping and vortex-induced vibrations of square cylinder [J]. Journal of Zhejiang University (Engineer Science),2005,39(4): 595-599.
[8] Revuz J,Hargreaves D M,Owen J S. Numerical simulation of the dynamic wind loading on and response of tall buildings[C].5th European & African Conference on Wind Engineering. 2009.
[9] 许媛欣. 方柱绕流涡激振动及控制方法的数值研究[D]. 天津:天津大学,2014.
[10] Chen W L,Li H,Ou J P, et al. Numerical simulation of vortex-induced vibrations of inclined cables under different wind profiles [J]. Journal of Bridge Engineering,2013,18(1):42-53.
[11] 王漢封,徐萌霞. 有限长正方形棱柱绕流的双稳态现象[J]. 力学与实践,2013,35(3):46-50.
Wang Hanfeng,Xu Mengxia. Bistabal phenomenon of the flow around a finite-length square prism[J]. Mechanics in Engineering,2013,35(3): 46-50.
[12] Sattari P,Bourgeois J A, Martinuzzi R J. On the vortex dynamics in the wake of a finite surface-mounted square cylinder[J]. Experiments in Fluids,2012,52(5):1149-1167.
[13] 梁枢果,吴海洋,陈政清. 矩形超高层建筑涡激共振模型与响应研究[J]. 振动工程学报,2011,24(3):240-245.
Liang Shuguo,Wu Haiyang,Chen Zhengqing. Investigation on model and responses of vortex-induced resonances of rectangular super high-rise buildings[J]. Journal of Vibration Engineering,2011,24(3): 240-245.
作者简介: 卢姗姗(1981-),女,高级工程师。电话:(0451)86282068;E-mail:lsshit@163.com
通讯作者: 陈文礼(1980-),男,教授。电话:15104518201;E-mail:cwl_80@hit.edu.cn
