铝合金受压板件局部屈曲承载力设计方法
2019-12-20袁霖张其林
袁霖 张其林


摘要:为考察现有铝合金设计规范预测非焊接受压板件承载力的准确性,采用壳单元建立单向受压四边简支板、方形截面管柱和十字形截面轴压柱有限元模型,使用ANSYS计算得到铝合金板件弹塑性屈曲临界应力和极限承载力。数值计算结果与理论分析结果对比发现:现有板件弹塑性屈曲应力理论能够给出铝合金板件屈曲临界应力的下限值,误差较小。中国规范非加劲板件有效厚度预测公式偏保守,因此给出修正的有效厚度预测公式。修正后的非加劲板件有效厚度公式可以提高板件利用率,增强经济性。
关键词:铝合金; 板件; 承载力; 有效厚度; 塑性; 屈曲; 局部稳定
中图分类号:TU512.4; TB115.1
文献标志码:B
Design methods for local buckling bearing capacity of
aluminum alloy members under compression
YUAN Lin, ZHANG Qilin
(College of Civil Engineering, Tongji University, Shanghai 200092, China)
Abstract:
To study the accuracy of existing aluminum alloy design standard for predicting the ultimate bearing capacity of non-welded plates under compression, the finite element model of simply supported plate, square-section column and cruciform-section column under axial compression is built using shell elements. The elastic-plastic buckling stress and ultimate bearing capacity of aluminum alloy members are obtained using ANSYS. The comparisons between numerical calculation results and theoretical analysis results show that the existing elastic-plastic buckling stress theories can lead the lower limits of critical buckling stress of aluminum alloy members with small error. The effective thickness predicting formulas of non-stiffened members in Chinese standard are conservative. The improved effective thickness prediction formulas are proposed. The utilization efficiency can be improved by using the suggested formulas on effective thickness of non-stiffened members, which is more economic.
Key words:
aluminum alloy; member; bearing capacity; effective thickness; plasticity; buckling; local stability
收稿日期:2019-07-23
修回日期:2019-08-28
基金项目: 国家自然科学基金(51738009)
作者简介:
袁霖(1995—),女,河北邯郸人,硕士研究生,研究方向为铝合金结构,(E-mail)yuanlin@tongji.edu.cn;
张其林(1962—),男,江苏海门人,教授,博导,博士,研究方向為铝合金结构,(E-mail)zhangqilin@tongji.edu.cn
0 引 言
铝合金具有轻质、高强度的优点,越来越多地被作为承重构件应用于大跨度屋盖中。[1-3]铝合金弹性模量小,局部稳定问题较为突出。与钢材不同,铝合金材料的应力-应变曲线连续光滑,没有明显的屈服平台,应力超过比例极限后随即进入应变硬化阶段。铝合金的这一特性对板件的屈曲临界应力和极限承载力有较大影响。目前,欧洲铝合金规范(Eurocode 9,以下简称“欧洲规范”)[4]和我国《铝合金结构设计规范》(GB 50429—2007,以下简称“中国规范”)[5]均根据材料硬化性能程度的不同分别定义受压板件全部有效的宽厚比限值和有效厚度公式中的计算因数α1、α2、C1和C2。本文分别应用BLEICH和STOWELL板件弹塑性屈曲理论[6]推导铝合金板件弹塑性临界屈曲应力预测公式,并在ANSYS软件中建立2种铝合金单板的双非线性有限元模型,模拟得到板件局部屈曲应力的精确值,然后对22个方形截面管柱和103个等边十字形截面轴压柱进行有限元分析,并把数值结果与中国规范、欧洲规范和美国铝合金设计手册(Aluminum Design Manual,以下简称“美国规范”)[7]的计算结果进行对比,以期为工程设计提供指导。
1 铝合金板件受压局部稳定承载力设计 方法简介
中国规范、欧洲规范和美国规范对板件类型描述对比见表1。同一类型的板件在不同规范中的定义不同,为统一描述,后文以中国规范中的定义进行表述。
1.1 有效厚度法
目前,中国规范、欧洲规范和英国的铝合金使用规范[8]都允许利用板件的屈曲后强度,并按照有效截面法考虑局部屈曲对构件整体承载力的影响,以便更好地发挥材料性能。考虑到铝合金挤压型材截面形状复杂性和加劲肋形式多样性,采用有效宽度法[9]进行设计会导致计算繁琐,因而中国规范沿用欧洲规范中的有效厚度法计算板件承载力。以宽度为b、厚度为t的单向均匀受压板件为例,有效宽度法的设计思路是,在达到极限承载力时,如果假定板件中间板带由于受约束较小承受的载荷也较小,大部分载荷由约束较强的板边承担,在有效宽度beff 范围内,板件的应力均达到屈服应力f0.2 ,板件的平均应力均为σm,那么板件的极限承载力为
Pu=σmbt=f0.2 beff t=f0.2 btbeff b=f0.2 btρc
(1)
式中:ρc为受压板件有效宽度的Winter公式系数,
ρc=1-0.222
(2)
式中:为板件的换算柔度系数。
按照有效厚度法计算板件承载力的公式为
Pu=σmbt=f0.2 bteff =f0.2 btteff t=f0.2 btρc
(3)
式中:teff 为板件的有效厚度。
中国规范中有效厚度折减系数ρc的计算公式沿用Winter公式的形式,只是针对铝合金硬化类型和板件类型的不同,取略有差异的计算因数α1和α2,即
ρc=tet=α1-
0.22α22
(4)
式中:te为考虑局部屈曲的板件有效厚度。
=f0.2 σcr =
btf0.2 E12(1-ν2)kπ2
(5)
式中:σcr 为屈曲临界应力。
对于加劲板件,k=4.0,=0.526btf0.2 E ;对于非加劲板件,k=0.425,=1.61 btf0.2 E。
欧洲规范针对边缘加劲薄柔板件的有效厚度折减公式为
ρc=C1β/ε-C2(β/ε)2
(6)
式中:β=b/t;ε=250/f0.2 。
取弹性模量E=68 000 MPa,泊松比ν=0.3,将欧洲规范中的有效厚度(式(6))转化为Winter公式(式(4))形式的等效计算因数α1和α2,见表2。
由表2可以看出,中国规范中的有效厚度公式计算因数α1和α2与欧洲规范中的有效厚度公式转化后得到的α1和α2非常接近。对于弱硬化合金加劲板件,其应变硬化指数n较大,应变硬化段不明显,应力-应变曲线接近钢材的理想弹塑性模型,所以有效厚度法的计算公式与Winter公式相同,即α1= 1.0、α2=1.0。对于强硬化合金,中国规范和欧洲规范都在弱硬化合金计算公式的基础上乘以0.9的折减因数。
1.2 许用应力法(抗力因数法)
美国规范的设计思路是给出板件允许承受的最大应力FL,该应力与板件的受力形式、宽厚比和材料热处理方式有关。当板件宽厚比超过S1时,需要考虑局部屈曲对板件极限承载力的影响。采用安全系数nu、ny和na或抗力分项系数y、c和确定板件的极限应力。对于不设加劲肋的加劲板件和非加劲板件,板件的极限应力为
FL=1
y f0.2 ,b/t≤S1
cBp-λDpbt,S1
ck2BpE/(λb/t),b/t≥S2
(7)
式中:
S1=(Bp-Fcy y/c)/λDp;S2=k1Bp/λDp;
Bp、Dp、k1和k2為与材料硬化类型有关的受压板件屈曲因数;
λ为与板件类型有关的常数,非加劲板件的λ= 5.1,加劲板件的λ=1.6。
1.3 规范中受压板件全部有效的宽厚比限值
以强硬化铝合金5083-H321和弱硬化铝合金6061-T6为例,非比例伸长屈服应力f0.2 分别取266 MPa和245 MPa,弹性模量E=68 000 MPa,泊松比ν= 0.3,计算得到相应受压板件全部有效的最大宽厚比,见表3。由此可以看出:按照美国规范计算公式确定的宽厚比限值,远小于中国规范和欧洲规范给出的结果,偏于保守;中国规范和欧洲规范给出的结果基本一致。
2 铝合金加劲板件屈曲性能和承载力分析
铝合金材料的应力-应变曲线有应变硬化区段,
且弹性模量只有钢材的1/3[10],因此其变形和屈曲问题较为复杂。先从理论上给出采用板件弹塑性屈曲理论推导得到的铝合金受压板件屈曲临界应力计算公式,再建立四边简支板单向受压有限元模型,研究铝合金板件的屈曲性能。由于均匀受压的方形截面管柱中各板件的宽厚比相同,所以各板件同时发生屈曲,板件交线将保持直线。假设交线边为简支[11],在有限元软件中建立方形截面管柱模型进行对比,分析规范中加劲板件设计公式的准确性。
2.1 铝合金板件塑性屈曲应力
2.1.1 基于BLEICH理论的铝合金板塑性屈曲应力
BLEICH理论认为,板件在弹塑性阶段屈曲时,可假定板件在x方向的抗弯刚度近似按比值Et/E(Et为切线方向弹性模量)减小,x方向对y方向的抗扭刚度按η=Et/E减小,y方向的抗弯刚度保持不变,即假定板件是正交异性的。根据这一假定,可得到板件的弹塑性屈曲微分方程为
Dη4wx4+2η4wx2y2+4wy4+σxt2wx2=0
(8)
采用与弹性屈曲相同的分析方法,可得到弹塑性阶段屈曲临界应力为
σcr,p =ηkπ2E12(1-ν2)(b/t)2
(9)
基于BLEICH理论,可给出用材料的切线模量Et确定铝合金板件非弹性屈曲应力σcr,p 的方法。Ramberg-Osgood模型可较好地描述铝合金材料的应力-应变关系[12],见式(10),进而可得到任一应力的切线方向弹性模量Et,见式(11),然后用等效切线模量代替弹性模量,可得到式(12)。
ε=σE+0.002σf0.2 n
(10)
Et=σε=11E+0.002nf0.2 σf0.2 n-1
(11)
σcr,p =Et(σcr,p )Eσcr,e
(12)
式中:Et(σcr,p )为材料应力-应变关系中当应力为σcr,p 时对应的切线弹性模量;σcr,e 为板件弹性屈曲临界应力。在铝合金板件的弹性屈曲分析中,通常引入板件的换算柔度系数表征板件的弹性屈曲临界应力σcr,e 与材料屈服强度f0.2 的关系,即
σcr,e =f0.2 2
(13)
将式(13)代入式(12),得到塑性屈曲应力σcr,p 与屈服强度f0.2 的关系为
σcr,p =Et f0.2 E2
(14)
引入板件屈曲臨界应力σcr 与屈服强度f0.2 的关系函数χ=σcr /f0.2 ,则有
χ=11+0.002Enf0.2 (χ)n-1 2
(15)
2=χ+0.002Enf0.2 (χ)n-1
(16)
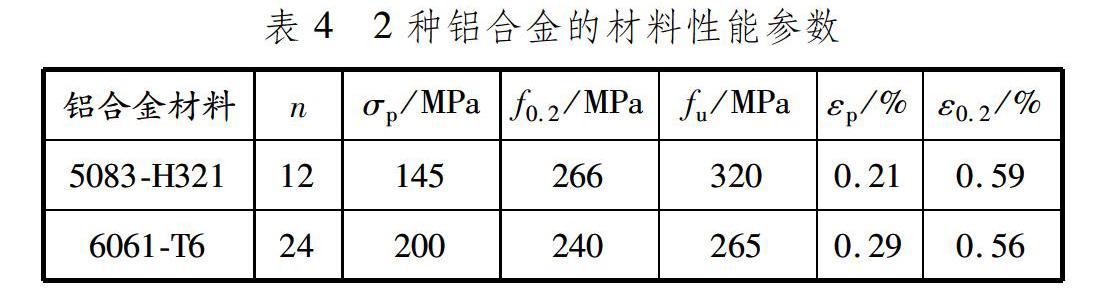
选取2种铝合金材料5083-H321和6061-T6,分别代表强硬化合金和弱硬化合金,研究材料的应变硬化性能对弹塑性屈曲载荷的影响。2种铝合金的材料性能参数见表4,其中的σp和εp分别为材料的比例极限应力和比例极限应变。
由式(15)可知,当为自变量时,无法得到χ的闭合解,故可先由χ确定,得到两者的关系曲线,见图1。
图1中的χ-关系曲线可以分为2部分:当较大即板件较薄时,板件在弹性阶段屈曲;当较小即板件不太薄时,板件在塑性阶段屈曲,在这个范围的塑性屈曲应力与之间没有闭合解,可由拟合直线近似确定。对于5083-H321铝合金,
χ=1.13-0.37
(17)
对于6061-T6铝合金,
χ=1.06-0.23
(18)
由此可得到2种材料基于BLEICH理论的屈曲临界应力的表达式,对于5083-H321铝合金,
σcr,t =(1.13-0.37f0.2 /σcr,e )f0.2
(19)
对于6061-T6铝合金,
σcr,t =(1.06-0.23f0.2 /σcr,e )f0.2
(20)
2.1.2 基于STOWELL理论的铝合金板塑性屈曲应力
文献[13]给出按照STOWELL理论求得的板件弹塑性屈曲应力为
σcr,p =kmin π2E12(1-ν2)(b/t)2
(21)
其中:kmin =2(1+1-ηs),ηs=34(1-Et/Es)。切线模量Et和割线模量Es都随屈曲应力的变化而变化,因此需要反复试算才能得到弹塑性屈曲应力σcr,p 。基于Ramberg-Osgood模型,可得到
Es=σε=σσE+0.002σf0.2 n
(22)
将式(11)、(22)代入式(21)中,结合χ的定义,可得到关系函数
χ=2+1+31/E+0.002/f0.2 (χ)n-1 1/E+0.002n/f0.2 (χ)n-1 2
(23)
类似地,当为自变量时,无法得到χ的闭合解,故可先由χ确定,得到两者的关系曲线(见图2),然后采用线性拟合的方法得到χ与之间的关系式,见式(24)和(26)。
相应地,基于STOWELL理论的塑性屈曲应力表达式见式(25)和(27)。
对于5083-H321铝合金,
χ=1.210-0.455
(24)
σcr,s =(1.21-0.46f0.2 /σcr,e )f0.2
(25)
对于6061-T6铝合金,
χ=1.079-0.252(26)
σcr,s =(1.08-0.25f0.2 /σcr,e )f0.2
(27)
2.2 受压加劲板件极限承载力分析
采用ANSYS进行数值模拟,用壳单元SHELL181建模,板件厚度取10 mm。对于四边简支板,板件长度a取板件宽度b的4倍,边界条件为四边简支,不约束非加载边的面内位移,见图3a),其中1为约束,0为不约束。对于方形截面管柱,取截面边长与四边简支板的宽度相等,厚度为10 mm,构件长度取截面高度的3倍,构件轴向网格宽度为20 mm。在上、下端面10 mm的位置设置参考点,施加铰接约束,见图3b)[14],其中1为约束,0为不约束。
在对实际结构进行弹塑性稳定分析时,考虑初始缺陷的影响。按照中国《铝合金建筑型材 第1部分:基材》(GB/T 5237.1—2008)[15]中的定义,当板件加工精度为超高精级(0.4%)时,缺陷幅值取板宽的0.4%。为力求减小缺陷幅值对屈曲临界力的影响,本文缺陷采用0.1%板宽的大小。材料采用Ramberg-Osgood模型,取20个应力、应变点构造多折线模型,考虑2种铝合金材料的性能参数。数值模拟时先对板件进行弹性屈曲分析,把第1阶屈曲模态作为初始缺陷形状施加到模型上,取板件宽度的0.1%作为缺陷幅值进行弧长法分析,得到板件的临界屈曲应力和极限承载力。
依据应变反向法,当板件承受压力载荷时,板件两侧表面为相等的压应力,随着外部压力载荷的增大,板件开始出现面外弯曲。[16]由于弯曲拉应力的出现,一侧板面的压应力开始减小,故选取板件屈曲半波上的点代表板面应力分叉的特征点(见图4)。
当6061-T6铝合金板件宽度为320 mm时,特征点板面x向压应力与板面应变关系曲线见图5。根据该点附近单元的表面应变变化特征,当2条曲线出现分叉时,表明一侧板面出现拉应变,板件开始屈曲,该点对应的应力即为屈曲应力。
6061-T6和5083-H321铝合金板件塑性屈曲临界应力有限元计算结果与屈曲理论预测值对比分别见表5和6,其中σcr,e 为按照式(2)计算得到的板件弹性屈曲应力,σcr,s 和σcr,t 分别为按照STOWELL屈曲理论和BLEICH屈曲理论计算得到的板件塑性屈曲应力的理论值,σcr,p 为有限元数值模型根据应变分叉法确定的板件弹塑性屈曲应力。由此可以看出,按照BLEICH理论得到的屈曲理论值略小于按照STOWELL理论确定的屈曲理论值,两者的计算值均小于有限元模拟得到的板件屈曲应力精确解,但误差很小,故认为可以采用BLEICH理论可以给出板件塑性屈曲临界应力的下限值,按照BLEICH理论和STOWELL理论均可以较准确地预测铝合金板件的塑性屈曲应力。
方形截面管柱的具体截面尺寸见表7,其中B为板件宽度,t为板件厚度,L为构件长度。试件编号中的“S5”表示材料为5083-H321,“S6”表示材料为6061-T6,后2位数字为板件的宽厚比。
方形截面管柱屈曲模态云图和极限承载力下的变形云图见图6。ANSYS模拟得到的四边简支板极限承载力下的板件平均纵向应力σplate 、方形截面管柱极限承载力下的截面平均轴向应力σsqu ,以及按照中国规范、欧洲规范和美国规范计算公式确定的板件极限应力预测值σGB 、σEC 和σADM 对比见表8。
由此可以看出:由四边简支板得到的板件平均纵向应力整体上与方形管柱很接近;中国规范和欧洲规范给出的承载力预测值很接近,与模拟结果的偏差在
10%以内,随着板件宽厚比增大,2个规范预测的误差减小;美国规范给出的板件承载力预测值整体上小于中国规范和欧洲规范,偏于保守。
3 铝合金非加劲板件承载力分析
工程中使用的T形截面板件和工形截面板件的翼緣均为非加劲板件,本文选取等边十字形截面轴压柱件进行分析,考察现有规范对于非加劲板件极限承载力计算公式的适用性和准确性。板件厚度均取10 mm,弱硬化合金6061-T6对应的板件宽厚比范围为5~16(共56个),强硬化合金5083-H321对应的板件宽厚比范围为4~13(共47个),可涵盖工程中常用尺寸构件中的非加劲板件宽厚比范围。材料性能参数、网格划分与前文的方形截面管柱均相同,十字形截面轴压柱长度取截面高度的10倍,对板件交线设置铰接约束,见图7,其中1为约束,0为不约束。等边十字形截面轴压柱屈曲模态和极限承载力下的变形云图见图8。
由于篇幅所限,只列出有限元数值模拟和规范对比结果的部分数据,见表9,其中:NGB 、NEC 和NADM 分别为按照中国规范、欧洲规范和美国规范计算得到的截面承载力,NFEM 为有限元模拟结果;
误差是指与中国规范的误差;
试件编号中“X5”表示材料为5083-H321,“X6”表示材料为6061-T6,右部的数字为板件的宽厚比。
由表9可以看出,中国规范和欧洲规范会低估
非加劲板件的承载力,有的误差在10%左右,尤其是当宽厚比增大时,规范结果会更加保守,造成材料不能充分利用。出于经济性考虑,本文基于有限元模拟结果,提出针对非焊接、非加劲板件有效厚度的建议修正公式,以期在保证安全性的基础上提高板件的利用率。
中国规范中用于计算非焊接弱硬化合金非加劲板件受压极限承载力的有效厚度公式为
tet=0.96-0.22×1.02≤1.0
(28)
对应的全部有效板件宽厚比限值[b/t]=6,等效柔度系数限值[]=0.582。
本文给出弱硬化合金有效厚度建议修正公式为
tet=1.1-0.22×1.32≤1.0
(29)
弱硬化合金非加劲板件有限元、中国规范和式(29)计算结果对比见图9。由此可知,修正公式与有限元数值模拟结果的差值很小,预测较精确。式(29)得到的板件等效柔度系数限值[]=0.679,对应的全部有效的板件宽厚比限值[b/t]=7.01。
中国规范中计算非焊接强硬化合金非加劲板件受压极限承载力的有效厚度公式为
tet=0.9-0.22×0.92≤1.0
(30)
对应的全部有效板件宽厚比限值[b/t]=7.39,等效柔度系数限值[]=0.512。
本文给出强硬化合金有效厚度修正公式为
tet=0.95-0.22×1.02≤1.0
(31)
式(31)沿用式(4)的形式,在系数确定上保证所有有限元的数据点均落在曲线上方,得到较为安全的有效厚度公式。
强硬化合金非加劲板件有限元、中国规范和式(31) 计算结果对比见图10。
式(31)对应的板件等效柔度系数限值[]=0.55, 对应全部有效的板件宽厚比限值[b/t]=5.5。
受压板件全部有效的最大宽厚比[b/t]与材料的非比例伸长应力f0.2 有关。中国规范中引入参数ε=240/f0.2 ,在本次分析中:选用6061-T6铝合金代表弱硬化合金,f0.2 =245 MPa,对应的ε=240/245=0.99,计算得到[b/t]=7.0,当采用其他强度的弱硬化合金时,推导得到对应的最大宽厚比[b/t]=7.0εηk′;选用5083-H321铝合金代表强硬化合金,f0.2 =266 MPa,对应的ε=240/266=0.95,计算得到[b/t]=5.5,当采用其他强度的弱硬化合金时,推导得到对应的[b/t]=5.8εηk′。公式修正前、后非焊接受压板件全部有效的最大宽厚比限值见表10。
4 结束语
铝合金的弹性模量较低,容易发生局部失稳。本文通过理论推导,得到基于BLEICH理论和STOWELL理论、按照Ramberg-Osgood本构模型确定的铝合金受压板件弹塑性屈曲临界应力近似表达式。对比单向受压的四边简支板有限元屈曲分析结果,认为推导得到的表达式能够较精确地预测板件的弹塑性屈曲临界应力。对22个等厚度方形截面管柱的数值模拟结果表明,中国规范能够较精确地预测铝合金非焊接加劲板件的极限承载力;对103个等边十字形截面轴压柱的数值模拟结果表明,中国规范会低估非加劲板件的有效厚度,同时给出优化后的非加劲板件有效厚度计算公式和相应的板件全部有效的最大宽厚比。
参考文献:
[1]王湛, 段德章, 潘建荣. 铝合金构件局部稳定问题的研究现状[J]. 钢结构, 2017, 32(6): 1-5. DOI: 10.13206/j.gjg201706001.
[2]常婷. 铝合金轴心受压构件局部稳定与相关稳定性能研究[D]. 北京: 清华大学, 2014.
[3]王元清, 常婷, 石永久, 等. 铝合金轴心受压构件局部整体相关稳定试验研究[J]. 土木工程学报, 2016, 49(1): 14-22. DOI: 10.15951/j.tmgcxb.2016.01.003.
[4]Eurocode9: Design of aluminum structures - Part 1-1: General structural rules: EN 1999-1-1:2007[S].
[5]铝合金结构设计规范: GB 50429—2007[S].
[6]BLEICHF. Buckling strength of metal structures[M]. New York: McGraw-Hill, 1952: 105-106.
[7]Aluminiumdesign manual: Specifications & guidelines for aluminum structures: TA690 .A45 2005 F[S/OL].
(2005-12-30)[2019-07-01]. https://searchworks.stanford.edu/view/5751294
[8]Structuraluse of aluminum: Part 1: Code of practice for design: BS 8118-1[S].
[9]LANDOLFOR, MAZZOLANI F M. Different approaches in design of slender aluminum alloy sections[J]. Thin-Walled Structures, 1997, 27(1):85-102. DOI: 10.1016/0263-8231(96)00015-8.
[10]季俊, 张其林, 黄政华. 基于有效厚度法的铝合金构件有效截面特性计算[J]. 计算机辅助工程, 2009, 18(4): 48-51. DOI: 10.3969/j.issn.1006-0871.2009.04.013.
[11]吕静, 郭剑, 王彬, 等. 基于ANSYS的角钢局部屈曲/后屈曲等效分析[J]. 计算机辅助工程, 2013, 22(6): 74-78. DOI: 10.3969/j.issn.1006-0871.2013.06.014.
[12]Descriptionof stress-strain curves by three parameters: NASA NACA-TN-902[S].
[13]吴亚舸. 铝合金受压板件局部屈曲与受弯构件弯扭屈曲承载力研究[D]. 上海: 同济大学, 2005. DOI: 10.7666/d.w1657626.
[14]常婷, 王元清, 石永久, 等. 铝合金轴压构件局部稳定的設计方法分析[J]. 建筑结构, 2015, 45(11): 32-36. DOI: 10.19701/j.jzjg.2015.11.007.
[15]铝合金建筑型材: GB/T 5237.1—2008[S].
[16]SOUTHWELLR V. On analysis of experimental observations in problems of elastic stability[J]. Proceedings of Royal Society A: Mathematical, Physical and Engineering Sciences, 1932, 135(828): 601-616. DOI: 10.1098/rspa.1932.0055.
(编辑 武晓英)
