黏滞阻尼器耗能增效减震系统理论及试验研究

何文福 黄祥博 张强 许浩 刘文光

摘要： 鉴于传统消能减震系统在层间位移较小时耗能效率有限，介绍了一种带位移放大装置的黏滞阻尼器增效减震系统，可通过放大阻尼器的相对变形提升系统耗能能力。基于该系统变形受力特性构建了其耗能增效及高阶效应力学模型，发现在阻尼器拉伸和压缩变形过程中存在不对称现象，进一步讨论了模型参数对力学性能的影响规律。设计制作了试验模型，并完成了在正弦荷载的作用下的往复加载试验。通过对比试验结果与理论曲线验证了理论力学模型的正确性，并通过试验探讨了频率相关性与疲劳性能。最后针对某框架?剪力墙减震结构进行地震响应分析，结果表明较少数量的带位移放大装置的黏滞阻尼器增效减震系统可实现数倍普通阻尼器的增效减震效果。

关键词： 耗能减震结构; 黏滞阻尼器; 位移放大; 性能试验; 地震响应

中图分类号： TU352.11; TU398+.2 文献标志码： A 文章编号： 1004-4523（2021）05-0879-10

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.001

引 言

地震作为一种常见的自然灾害，给人类带来了巨大的人身和财产损失。地震中建筑物的破坏与倒塌，是造成损失的最主要原因[1]，因此结构抗震研究对减少地震灾害有着重要意义。传统抗震通过结构自身性能抵御地震作用，不具备调节与控制作用，无法适应多变的地震荷载。为解决这一弊端，结构振动控制技术应运而生，其通过在结构上设置控制机构，使结构的动力反应减小，是一种有效的结构抗震手段。其中，被动振动控制因其构造简单、减震机理明确、造价低、易于维护且无需外界能源支持等优点而被大量应用[2?4]。消能减震作为一种被动控制手段，将输入结构的地震能量引向附加设置的机构和元件加以吸收和耗散，从而能够保护主体结构的安全。其常用的耗能元件[5]包括：黏弹性阻尼器[6]、黏滞阻尼器[7]、金属阻尼器、摩擦阻尼器等。

当阻尼器布置位置与数量受限，结构变形较小或变形速度较慢时传统阻尼器弊端开始显现[8?9]，因此学者提出了多种装置与布置方式以实现放大阻尼器的变形和提高阻尼器的变形速度，增大阻尼器的耗能。陈月明等[10]提出一种附加梯形杠杆摆的黏弹性阻尼器，通过设置人字形支撑与杠杆原理将结构位移放大作用于阻尼器，进而减少地震与强风作用下的结构响应。Constantinou等[11]率先提出了基于连杆机构的位移放大系统，并应用于一些实际工程实例中;Sigaher等[12]又在此基础上进一步分析了多种剪刀型布置方法对阻尼器耗能的影响;Stefano等[13]采用在机械领域应用颇为广泛的齿轮齿条加速器来放大结构振动传给阻尼器的位移。Watakabe等[14]提出一种带位移放大功能的管形黏弹性阻尼器，试验结果表明该阻尼器对结构振动响应的控制效果较好。刘文光等[15]提出了一种位移放大型阻尼墙，从理论上分析其增益效果，并且进行了相关的振动台试验与数值分析，结果表明该阻尼墙减震效果显著。

黏滞阻尼器（Viscous Damper，VD）因其工作频域宽及阻尼力与位移存在π/2相位差，安装连接简易等特性而被广泛采用，成为最常见的消能减震元件之一。本文提出了一种附加位移放大装置的黏滞阻尼器增效减震系统（Enhanced Damping System with Viscous Damper with Displacement Amplifier，SDA），并构建了理论模型，完成了模型试验，最后进行了减震结构的地震响应分析。

1 SDA构造及其理论分析

1.1 黏滞阻尼器耗能增效减震系统构造

图1为筒式黏滞阻尼器构造示意图，该类阻尼器主要由装有黏滞流体的缸体和可在其中活动的活塞及活塞杆、附缸组成，在激励荷载作用下，活塞杆在缸体内移动，迫使受压流体通过孔隙或缝隙，进而产生阻尼力[16?17]。

黏滞阻尼器耗能增效减震系统由人字形斜撑、连接板、位移放大杠杆、支点固定架、黏滞阻尼器等组成。通过在阻尼器与结构之间增设位移放大杠杆，使得地震时阻尼器的变形数倍于结构变形，增加阻尼器耗能与结构附加阻尼。具体形式如图2（a）所示，人字形斜撑两端分别与梁柱节点、连接板通过螺栓固接，连接板附有耳叉，耳叉开有长圆孔，以满足系統工作时杠杆的运动协调要求，位移放大杠杆分别与连接板、支点固定架、黏滞阻尼器通过销轴铰接，黏滞阻尼器固定端与结构梁柱节点铰接，支点固定架与梁柱节点固接。

1.2 SDA理论模型

地震时，结构的位移通过人字形支撑传递给杠杆上端，经杠杆的放大作用于阻尼器。阻尼器和杠杆的运动如图2（b）所示，图中m，k，c，u分别表示结构的质量、刚度、阻尼和层间位移;为杠杆放大倍率;为附加阻尼器阻尼;M点为支点转动轴。结构变形时，杠杆围绕支点转动，阻尼器两端的相对位移为结构变形的倍，即此时阻尼器变形为。

普通筒式黏滞阻尼器为速度型阻尼器，其阻尼力和耗能可表示为[18]：

式中 表示阻尼器的阻尼系数;表示阻尼器两端的相对速度;是符号函数;表示阻尼器的阻尼指数，一般常用范围为0.3?1.0;，分别表示阻尼力、位移关于时间的函数。

从式（4）?（5）可以看出，对于SDA，减震系统阻尼力与耗能都变为原阻尼器的倍。

如果将普通黏滞阻尼器的阻尼系数放大n倍，则其阻尼力与耗能分别为：

1.3 考虑变形高阶效应耗能的SDA模型

结构发生层间变形时放大杠杆绕支点轴转动，上述理论分析未考虑杠杆的摆动对阻尼器变形的影响，考虑杠杆摆动时，阻尼器存在变形高阶效应，其活动端运动轨迹如图2（c）所示，图中M点为杠杆支点;O点为阻尼器固定端;ΔS1，ΔS2分别为加载位移为±u时阻尼器的压缩变形与拉伸变形，杠杆动力臂长度为d;L为阻尼器初始长度。可以看出阻尼器活动端运动轨迹呈弧线，阻尼器变形与结构变形关系非简单的，且相同位移下压缩变形ΔS1小于，拉伸变形ΔS2大于，即可得出相同位移的情况下阻尼器拉伸变形大于压缩变形，阻尼器运动为非对称过程。

考虑变形高阶效应后阻尼器活动端水平位移、竖向位移的表达式为：

根据上述理论绘制考虑变形高阶效应的理论模型（Higher Order Model，HOM）和未考虑变形高阶效应的理论模型（Normal Model，NM）的滞回曲线如图3所示。可以看出，考虑变形高阶效应时SDA耗能为非对称过程，阻尼器拉伸耗能大于压缩耗能。

1.4 参数影响分析

由式（11）?（12）可知，HOM模型中影响结构耗能的参数有：加载位移、加载频率、放大倍率、杠杆长度、阻尼器长度、阻尼指数、阻尼系数。为研究不同放大倍率、位移、阻尼器长度的情况下，考虑变形高阶效应对SDA耗能与耗能不对称性的影响，设定基准工况为加载位移20 mm，阻尼器长度1 m，阻尼指数为0.45，杠杆动力臂为0.18 m，加载频率为0.5 Hz。

图4展示了不同加载位移下变形高阶效应对阻尼器耗能的影响，考虑变形高阶效应后，阻尼器耗能增加，耗能提升率和耗能不对称性随加载位移和放大倍率的增大而升高，其中耗能提升率较小，在加载位移为60 mm，放大倍率为4倍时，耗能提升率仍小于0.6%，此时拉伸耗能相对提升9.85%。

图5展示了不同阻尼器长度下变形高阶效应对阻尼器耗能的影响。耗能提升率和耗能不对称性随阻尼器长度的减小和放大倍率的增大而升高。耗能提升率在不同阻尼器长度的情况下变化较小，实际工程中常用阻尼器长度在0.75?1.5 m之间，放大倍率为2?4倍时，耗能提升率小于0.11%，拉伸耗能相对提升为0.93%?4.44%。

考虑变形高阶效应后，阻尼器耗能提升率较小，实际工程中可以忽略耗能提升带来的影响，但阻尼器耗能不对称性较为明显。

2 力学试验的设计与方案

2.1 加载设备与试验模型

试验所采用设备为100 kN水平液压拉力试验机，最大作动速度为0.565 m/s。为配合试验设备，设计试验方案如图6（a）所示，作动器连接板下耳叉开有长圆孔，杠杆上端与作动器连接板铰接，初始状态为杠杆上孔对齐长圆孔上端，以满足试验过程中的位移协调要求;杠杆支点处与支点固定架铰接;杠杆下端与阻尼器活动端铰接;支点固定架与阻尼器固定端分别通过工装与下锚固板固接。

试验所采用筒式黏滞阻尼器阻尼系数为32 kN/（m/s）0.42，阻尼指数α为0.42。黏滞阻尼器、位移放大杠杆尺寸形式如图6（b）所示，杠杆动力臂长度为90 mm，力臂长度为270 mm，放大倍率为3倍，采用材料为Q345钢材，图6（c）为现场加载图。

加载时放大装置受力较大，且主要变形为杠杆动力臂和力臂的受弯变形，动力臂和力臂受弯变形问题可简化为梁端受集中荷载作用的悬臂梁挠度问题。经计算得在设定工况下动力臂最大挠度为0.2 mm，力臂最大挠度为1.8 mm，杠杆产生的变形对试验结果影响较小。

2.2 加载工况

试验采用位移控制的正弦加载，除疲劳性试验工况加载45个周期外，其他工况每次加载为5个周期，并取第3圈滞回曲线的数据用于确定阻尼器的性能指标，试验工况如表1所示。

试验过程的误差控制包括：尽量减少销轴与轴孔的间隙并使用硅脂润滑;每个工况结束后等待阻尼器冷却至室温再进行下次加载;保证加载前作动器与作动器连接板之间紧密贴合;为减少不同阻尼器之间的性能误差带来影响，使用同一个阻尼器分别进行普通型与放大型试验进行试验结果对比。

3 试验结果与分析

3.1 VD试验结果

图7（a）是普通黏滞阻尼器在加载位移为60 mm，加载频率分别为0.13，0.4，0.8 Hz，即加载速度幅值分别为50，150，300 mm/s时的试验滞回曲线，各工况下试验曲线饱满，随加载频率增加，阻尼器阻尼力与耗能增加。

图7（b）给出了最大阻尼力试验结果与理论值的对比，阻尼力随加载位移与加载频率的增大而增大，各工况试验最大阻尼力与理论值偏差平均小于5%。所采用黏滞阻尼器性能稳定，试验结果与理论值基本吻合。

3.2 SDA试验结果与分析

图8为SDA试验曲线与理论曲线的对比。SDA最大阻尼力与滞回面积的试验与理论值基本一致，阻尼器拉伸变形阶段曲线面积大于压缩阶段，即滞回曲线呈非对称状。放大型阻尼器试验滞回曲线带有斜率，其原因主要是放大装置存在一定的间隙与弹性变形，但曲线表现出的偏差较小，可认为不影响SDA整体耗能效果。

表2给出了SDA和VD的阻尼力及耗能对比，在加载频率为0.13，0.40，0.80 Hz时，SDA最大阻尼力分别为VD的4.60，4.82，5.71倍，平均为5.04倍;耗能分别为VD的4.73，4.76，5.26倍，平均为4.92倍，与NM模型结果预测倍数4.76倍相近，且附加放大装置后系统阻尼力与耗能均有大幅增加，单组SDA与5个VD作用相当。对比SDA试验值与理论值，各工况下平均误差在10%以内。

3.3 频率相关性

一般认为加载频率对传统黏滞阻尼器的性能表现基本没有影响，但考虑附加放大装置后，阻尼器运动发生了变化，且放大装置存在一定的間隙与弹性变形，本节从一定加载速度和一定加载位移两个角度对SDA力学性能的频率相关性进行研究。

图9（a）为加载速度峰值为50 mm/s时，SDA在各作动频率下的试验滞回曲线。根据HOM理论分析，速度峰值一定的情况下，加载频率越低，位移越大，系统运动非对称性越强，最大阻尼力也就越大。试验结果显示，随加载频率的增加，阻尼力降低，与理论分析结果趋势一致。但试验结果显示最大阻尼力在0.32?1.59 Hz内降低11%，大于理论值2%。分析认为随着频率增高，加载位移减小，放大装置的间隙与弹性变形所占加载位移的比例增大，误差影响增加，从而导致阻尼力降低，即由于附加放大装置的构件间隙与弹性变形的存在，加载速度相同时，SDA阻尼力随加载频率的提高而降低。

图9（b）为一定加载位移下，作动频率对SDA试验最大阻尼力的关系图。结果表明试验数据与理论值基本吻合，平均误差为6.88%，最大误差为14%。试验结果表明，在同样的加载位移下，加载频率越高，SDA阻尼力越大，耗能越多。

3.4 疲劳性能

图10给出了SDA的疲劳性能试验第3至第45圈的滞回曲线，可以看出在加载45圈后SDA滞回曲线整体仍然饱满，形状基本与加载第3圈的曲线保持一致。加载第3圈阻尼器耗能为3073 J，加载第45圈耗能为3020 J，耗能减少1.77%;加载第3圈最大阻尼力为46.1 kN，加载45圈最大阻尼力为46.3 kN，疲劳试验中SDA最大阻尼力未出现明显衰减，加载循环圈数对阻尼器性能影响较小。

4 工程算例有限元分析

4.1 计算模型

选取某实际框架?剪力墙结构作为工程算例进行分析，该结构地上八层地下一层，地上高度为32.6 m。抗震设防烈度为8度，设计基本地震加速度为0.3g，设计地震分组为第二组，场地类别为Ⅲ类，结构一阶周期为0.59 s，二阶周期为0.572 s。

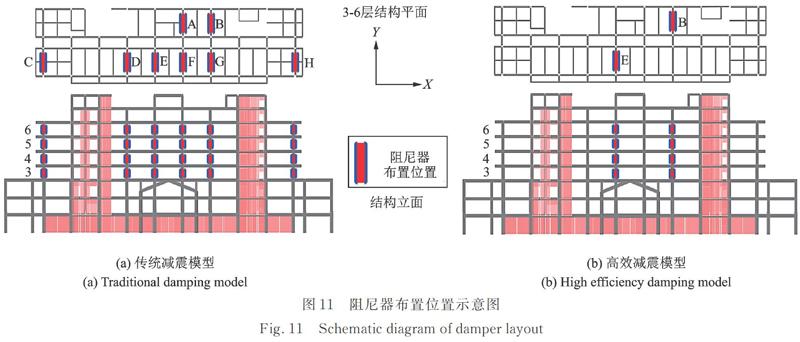
为研究SDA减震效果与变形高阶效应对减震效应的影响，分别对未加装减震装置的原结构（Regular Structure，RS）、附加传统黏滞阻尼器的普通减震结构（Viscous Damper?Structure，VD?S）、根据NM理论附加3倍放大SDA的减震结构（SDA?NM）、根据HOM理论附加3倍放大SDA的减震结构（SDA?HOM）四种模型进行动力响应分析。其中SDA?NM单个阻尼器阻尼系数为VD?S的倍，SDA?HOM中阻尼器参数与VD?S中相同，但在阻尼器与结构之间附加了位移放大装置。SDA?HOM中人字形斜撑、阻尼器铰座、支点固定架均使用刚性连接单元模拟，与阻尼器和杠杆连接端使用铰接，与结构连接端使用固接;杠杆动力臂使用无轴向刚度的框架单元模拟，杠杆力臂使用刚性框架单元模拟，动力臂与力臂固接。阻尼器布置方案与编号如图11所示，为最大程度发挥阻尼器性能，将阻尼器布置于结构变形较大的3?6层，各阻尼器均附加在结构Y向，不同方案的阻尼器参数如表3所示。

4.2 减震效应分析

采用5条天然波与2条人工波做地震荷载进行多遇地震下结构弹性时程分析，并使用其中2条天然波和1条人工波的前12 s做地震荷载进行设防地震和罕遇地震下结构弹塑性时程分析。表4展示了多水准地震荷载下结构的动力响应与附加阻尼系统性能表现。

相较RS，VD?S，SDA?NM，SDA?HOM顶层加速度、基底剪力、位移角峰值等动力响应均有效降低，且三种减震结构动力响应接近。图12为结构在罕遇地震RH3波作用下结构最终弹塑性发展情况，大部分框架梁出现塑性铰，RS与VD?S个别框架柱出现塑性铰，SDA?NM与SDA?HOM框架柱未出现塑性铰，结构主体完好，承载构件未出现破坏现象。

多水准地震下RH3波作用时SDA?NM与SDA?HOM的6?B阻尼器阻尼力分别为VD?S中的4.56?4.93倍、4.76?5.27倍;耗能分别为VD?S中的4.28?5.16倍、4.19?5.07倍。图13为VD?S，SDA?NM，SDA?HOM三种模型在RH3波作用下阻尼器6?B的滞回曲线对比，SDA?NM与SDA?HOM中阻尼器滞回曲线相近且相较VD?S更为饱满，罕遇地震下能观察到SDA?HOM中变形高阶效应的影响。

在三种地震水准下VD?S，SDA?NM，SDA?HOM的附加阻尼比接近，附加8组放大型阻尼器与附加32组普通阻尼器所能提供的附加阻尼比相当，且变形高阶效应所导致的阻尼器耗能不对称性对附加阻尼系统影响较小。图14为设防地震下四种模型在RH3波作用时的结构耗能时程图，VD?S，SDA?NM，SDA?HOM相较RS结构耗能均降低，三者附加的阻尼系统耗能分别为770，880，860 kJ。

5 结 论

本文提出了一种带位移放大装置的黏滞阻尼器增效减震系统，并构建了理论模型，完成了模型试验，最后进行了减震结构的地震响应分析，得到主要结论如下：

（1）带位移放大装置的黏滞阻尼器增效减震系统通过附加位移放大杠杆，增大阻尼器位移与速度来达到增加耗能的效果，位移放大倍的阻尼器，其阻尼力与耗能可提升倍。通过变形分析发现了阻尼器的变形高阶效应，拉伸和压缩状态下滞回曲线不对称，放大倍率越大，差别越明显。

（2）完成了3倍放大阻尼器和普通阻尼器的性能对比试验，试验滞回曲线与理论预测基本吻合，SDA的峰值出力为普通型的4.60?5.71倍，耗能为普通型的4.73?5.26倍;试验中观察到显著的拉伸压缩不对称特性，加载位移一定时，阻尼力随频率增大而增大，加载速度一定时，阻尼力随频率的变化范围在11%以内;加载45圈后单圈耗能仅减少1.77%，具有良好的抗疲劳性能。

（3）以某框架?剪力墙结构作用算例进行了地震响应分析，附加8组SDA的结构与附加32个VD的结构动力响应和附加阻尼比接近;单个SDA阻尼力为VD的4.56?5.27倍，耗能为VD的4.28?5.16倍;从结构响应控制、阻尼器性能表现等方面来看单个SDA可发挥4个以上VD的作用。变形高阶效应对附加阻尼器增效减震系统的减震结构影响较小。

参考文献：

[1] 阎维明，周福霖，谭 平.土木工程结构振动控制的研究进展[J].世界地震工程，1997，13（2）：8-20.

Yan Weiming， Zhou Fulin， Tan Ping. Development of vibration control for civil engineering structures[J]. World Information on Earthquake Engineering， 1997，13（2）：8-20.

[2] 翁大根，張 超，吕西林，等.附加黏滞阻尼器减震结构实用设计方法研究[J].振动与冲击，2012，31（21）：80-88.

Weng Dagen， Zhang Chao， Lü Xilin， et al. Practical design procedure for a energy-dissipated structure with viscous dampers[J]. Journal of Vibration and Shock， 2012，31（21）：80-88.

[3] Yao J T P. Concept of structural control [J]. ASCE Journal of the Structural Division， 1972， 98（ST7）： 1567-1573.

[4] 周 云，吴从晓，邓雪松.铅黏弹性阻尼器的开发、研究与应用[J].工程力学，2009，26（S2）：80-90.

Zhou Yun， Wu Congxiao， Deng Xuesong. Development， research and application of lead viscoelastic damper [J]. Engineering Mechanics， 2009，26（S2）：80-90.

[5] 欧进萍，吴 斌，龙 旭.耗能减振结构的抗震分析与设计方法[J].振动工程学报，1999，11（2）：55-62.

Ou Jinping， Wu Bin. Long Xu. Seismic design approaches of passive energy dissipation systems[J]. Journal of Vibration Engineering. 1999，11（2）：55-62.

[6] Zhang R H，Soong T T.Seismic design of viscoelastic dampers for structural applications[J]. ?Journal of Structural Engineering， ASCE， 1992， 118（5）： 1375-1392.

[7] Mc Namara R J， Taylor D P. Fluid viscous dampers for high-rise buildings[J]. The Structural Design of Tall and Special Buildings， 2003， 12（ 2） ： 145- 154

[8] 汪志昊，陈政清.高层建筑结构中黏滞阻尼器的新型安装方式[J].世界地震工程，2010，26（4）：135-140.

Wang Zhihao， Chen Zhengqing. New installations of viscous dampers in high rise buildings [J]. World Earthquake Engineering，2010，26（4）：135-140.

[9] Londo?o Julián M， Neild Simon A， Wagg David J. Using a damper amplification factor to increase energy dissipation in structures?[J]. Engineering Structures， 2015， 84： 162-171.

[10] 陈月明，刘 季.杠杆黏弹性阻尼器及其受控制结构的试验研究[C].第一届全国结构控制会议论文集. 1998.

Chen Yueming， Liu Ji. Experimental study on lever viscoelastic damper and controlled structure [C]. Proceedings of The First National Conference on Structural Control. 1998.

[11] Constantinou M C， Tsopelas P， Hammel W， et al. Toggle-brace-damper seismic energy dissipation system [J]. Journal of Structural Engineering，ASCE，2001，127（2）： 105-112.

[12] Sigaher A N， Constantinou M C. Scissor-jack-damper energy dissipation system[J]. Earthquake Spectra， 2003， 19（1）： 133-158.

[13] Stefano Berton， Bolander John E. Amplification system for supplemental damping devices in seismic applications[J]. Journal of Structural Engineering， ASCE，2005，131（6）：979-983.

[14] WATAKABE Tomoyoshi， FUJITA Satoshi. Research and development of vibration control device suitable for detached houses by using displacement amplification mechanism[J]. Journal of System Design and Dynamics，2009，3（3）：368-379.

[15] 刘文光，董秀玲，何文福，等.位移放大型阻尼墙减震结构的模型试验与数值分析[J].振动工程学报，2015，28（4）：601-609.

Liu Wenguang， Dong Xiuling， He Wenfu， et al. Dynamic tests and numerical response analysis of new energy dissipated structures with displacement amplification damper[J]. Journal of Vibration Engineering， 2015，28（4）：601-609.

[16] Taylor D P， Constantinou M C. Test methodology and procedures for fluid viscous dampers used in structures to dissipate seismic energy [R] .Taylor Devices， Inc. Technical Report， April 28， 1994.

[17] 汪大洋，周 云，王燁华，等. 黏滞阻尼减震结构的研究与应用进展[J].工程抗震与加固改造，2006，28（4）：22-31.

Wang Dayang， Zhou Yun， Wang Yehua， et al. State-of-the-art of research and application on structures with viscous damper[J]. Earthquake Resistant Engineering and Retrofitting，2006，28（4）：22-31.

[18] 翁大根，卢著辉，徐 斌，等. 黏滞阻尼器力学性能试验研究[J].世界地震工程，2002，18（4）：30-34.

Weng Dagen， Lu Zhuhui， Xu Bin， et al. The experimental study on property of energy dissipation of viscous liquid damper[J]. World Earthquake Engineering， 2002，18（4）：30-34.

作者简介： 何文福（1979-），男，博士，副教授。电话：13795219128; E-mail：howunfu@shu.edu.cn

通讯作者： 张 强（1988-），男，硕士，实验师。电话：（021）66131055; E-mail：zqiang88@t.shu.edu.cn