大档距特高压覆冰输电线路起舞风速TTMD控制优化研究

楼文娟 温作鹏 梁洪超

摘要： 针对大档距特高压输电线路舞动难以防治的问题，设计了一种电涡流扭转向调谐质量阻尼器（TTMD），并论证了相比于竖向阻尼器具有更强的适用性。从整档线路力学模型出发，推导了整档线路覆冰导线?TTMD系统的舞动偏微分方程，选取全局形函数离散得到常微分方程，采用李雅普诺夫稳定定理计算起舞风速。建立基于遗传算法的TTMD防舞优化设计方法，考虑到真实环境中导线覆冰偏角存在较大的不确定性，以大范围多覆冰偏角下导线最小起舞风速为优化目标，对TTMD的频率比、阻尼比、质量比、安装位置、导线张力、覆冰质量等参数进行优化设计。以某500 m大档距特高压输电线路覆冰八分裂导线为例进行优化设计，计算结果表明：当质量比高于0.005时，TTMD即可有效地提高最小起舞风速;TTMD的推荐安装位置范围为导线左侧1/4跨?右侧1/4跨;TTMD控制效果具有良好的鲁棒性;设计TTMD时，应当采用较高的导线张力、较低的覆冰质量设定，以得到偏于安全的TTMD参数设计值。

关键词： 风致振动; 覆冰多分裂导线; 防舞; 特高压; 扭转向调谐质量阻尼器 （TTMD）

中图分类号： TU312+.1; TM752+.5 文献标志码： A 文章编号： 1004-4523（2021）05-0934-09

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.006

引 言

为适应不断增长的电力需求，近年来中国有越来越多的特高压线路建成使用。覆冰特高压线路在风力作用下舞动现象时有发生，对电力安全造成威胁[1]。特高压线路的杆塔高度提升，导线分裂数增加，一旦发生舞动，其振动能量较大，防治难度相比于一般线路更大。对于大档距特高压线路的舞动防治，目前已有相间间隔棒、回转式间隔棒、相地间隔棒、双摆防舞器等，这些措施虽起到一定作用，但均存在一些局限性。因此，研究更为有效的舞动控制措施，对减少特高压线路破坏，保障电力安全具有重要意义。

现有的舞动机理研究表明，气动负阻尼是导致输电线路舞动的根本原因[2?5]，因此提高导线结构阻尼是一种有效的舞动控制方式。调谐质量阻尼器（Tuned Mass Damper，TMD）是一种被广泛应用的阻尼器，其在输电线路防舞中的应用研究已初步开展[6?9]，研究表明调谐质量阻尼器能够有效增加起舞风速并减小舞动幅值。但这些研究仅对单一覆冰偏角条件下TMD的有效性进行了验证，然而多分裂导线的气动力特性非常复杂，不同覆冰偏角工况下导线舞动特性存在较大差异。一种好的防舞策略不仅仅只是针对某一固定覆冰偏角有效，而是要对恶劣天气下可能出现的大范围多覆冰偏角情况下的舞动防治均有效，因此，本文以大范围多覆冰偏角下导线最小起舞风速为优化目标进行防舞优化设计。

现有研究中的TMD均针对导线的竖向运动进行控制，但大档距导线的自振频率较低，TMD的弹性元件静态伸长量可长达数米，可能引发碰撞问题，因此TMD对大档距特高压线路难以适用。另外，大档距多分裂导线的竖向频率与扭转频率较为接近，其舞动往往表现出竖?扭耦合的特点，扭转向运动对于舞动激发相当重要，因此采用扭转向调谐质量阻尼器（Torsional Tuned Mass Damper， TTMD）进行防舞在原理上是可行的。TTMD运行空间要求小，不存在自重引起的竖向变形，能够普遍适用于各种档距的多分裂线路舞动的防治，尤其可以应用于竖向TMD不再适用的大档距线路。

三自由度节段模型是导线舞动分析常用的模型[1]，但该模型无法考虑多阶耦合，也无法进行阻尼器安装位置的优化。因此，有必要针对TMD难以适用的大档距输电线路，建立加装TTMD的覆冰导线整档线路模型，研究大范围覆冰偏角下TTMD对大档距特高压输电线路的舞动控制效果。

阻尼器的参数、安装位置决定了阻尼器对结构的控制效果，对这些参数的优化是阻尼器设计的关键。遗传算法是一种借鉴自然选择、自然遗传机制的随机搜索算法，具有较高的计算效率，在土木结构的振动控制领域已有广泛应用[10?11]。Hervé等[10]针对加装TMD的多层木结构采用遗传算法对TMD参数进行优化，并检验了不同地震波下的控制效果。陈鑫等[11]针对风荷载作用下加装调谐液体阻尼器的高耸钢烟囱结构，采用遗传算法展开多目标优化，对结构响应及阻尼器行程取得良好控制效果。

本文针对大档距特高压输电线路舞動防治设计了一种电涡流扭转向调谐质量阻尼器，并进行优化研究。推导整档覆冰导线?TTMD系统的运动方程，采用李雅普诺夫稳定定理计算起舞风速;建立基于遗传算法的TTMD防舞优化设计方法，以大范围多覆冰偏角下导线最小起舞风速为优化目标，对TTMD各项参数进行优化设计;以某500 m大档距特高压输电线路覆冰八分裂导线为例，研究TTMD控制效果与频率比、阻尼比、质量比、安装位置、导线张力、覆冰质量等参数的关系，验证TTMD对起舞风速控制效果的有效性和鲁棒性。

1 计算方法

1.1 TTMD?覆冰导线运动方程及舞动稳定判定

本文对多分裂导线舞动计算作以下假设[12?13]：（1）各子导线物理参数一致，不考虑弯曲变形;（2）刚性间隔棒均匀分布，对于子导线运动完全约束;（3）风荷载满足准定常假定;（4）导线沿长度方向均匀覆冰。

自重作用下导线形状受导线张力控制，利用下式迭代计算可得导线覆冰后的新张力[14]

式中 H0和H分别为覆冰前、后的导线张力，E为导线弹性模量，A为导线截面积，Ls为单跨导线档距，q0和q分别为覆冰前、后的导线竖向均布荷载。

多分裂导线的整体坐标系定义如图1所示，s为沿导线轴向的坐标。

导线整体运动位移可表示为轴向位移u、竖向位移v、水平（面外）位移w和扭转位移θ，导线上第j个TTMD扭转移为θdj。通过汉密尔顿原理推导得覆冰导线?TTMD系统运动的偏微分方程

式中 分别为质量矩阵、增量刚度矩阵、阻尼矩阵、增量位移、增量荷载。根据式（6），采用Newmark?β法进行计算可得导线运动时程。

李雅普诺夫第一稳定定理[15]证明了可以根据非线性系统的线性化方程，即一次近似方程的特征值实部正负，判断非线性系统的稳定性。舞动作为典型的气动失稳现象，也可以通过计算运动方程的线性化方程特征值从而快速判断是否发生舞动。若特征值实部均为负，则表明系统稳定;若存在某一特征值实部为正，则表明系统失稳。式（6）的特征值可通过其Jacobi矩阵进行计算[16]

式中 为零矩阵，其所有元素均为0，为单位对角矩阵，除对角元素为1外，其余均为0。与分别为矩阵的特征值与对应特征向量，和分别为系统初始状态（即位移和速度都为0）时的总刚度矩阵和总阻尼矩阵，其值如下

式中 为气动阻尼矩阵，为气动刚度矩阵。

1.2 考虑覆冰偏角范围的防舞优化设计遗传算法

真实环境中导线非圆截面偏心覆冰一般形成于线路迎风侧。随着冰风气候条件的变化，导线的覆冰方向会发生偏转，覆冰偏角存在一定的变化范围。导线覆冰偏角定义如图2所示。

采用p个TTMD对整档覆冰导线进行舞动控制，TTMD参数的优化模型建立如下

式中 Ucri为优化目标，即0°?α0覆冰偏角范围内各个覆冰偏角下起舞风速的最小值（下文简称“最小起舞风速”）;X为设计变量;λdj，ζdj，sdj分别为第j个TTMD的频率比、阻尼比、位置参数。其中频率比（λd）定义为TTMD频率与导线一阶扭转频率之比，覆冰偏角α0的取值可根据导线覆冰偏角的统计资料确定。通过该优化模型，在预设参数范围内对TTMD参数进行优化，使得大范围覆冰偏角下导线最小起舞风速实现最大化。

本文设计的TTMD安装在多分裂导线的间隔棒上，目前关于间隔棒的安装位置并无统一规定，因此需要考察安装在不同位置时，TTMD能实现的最优控制效果。TTMD的位置参数（sd）定义为TTMD距导线端部距离与档距的比值，sd=0.5即对应导线跨中位置。需要注意的是，设计变量X分为两种情况：1）X包括sd，即安装位置是待优化参数之一;2）X不包括sd，即在给定安装位置前提下对TTMD参数进行优化。

本文采用遗传算法搜寻最优TTMD参数。遗传算法是一种通过模拟生物进化中“适者生存”的规律，采用选择（Selection）、交叉（Crossover）和变异（Mutation）操作，从而不断优化每一代种群适应度的迭代优化算法。其原理易于理解，有较强的鲁棒性且适用于并行计算，因此具有广泛应用。本文遗传算法的选择、交叉、变异操作分别选取轮盘赌选择法、算数交叉法、均匀变异法。采用遗传算法对TTMD参数的优化设计流程如图3所示。

优化的主要步骤如下：

1）首先随机生成阻尼器参数作为初始种群，设定覆冰偏角和初始风速;

2）通过判断TTMD?整档导线系统的Jacobi矩阵特征值实部是否大于0计算得到某覆冰偏角下的起舞风速;

3）输出0°?α0覆冰偏角范围内最小起舞风速，作为个体适应度;

4）评估种群中所有个体适应度并按照大小排序，通过选择、交叉、变异等操作得到子代新个体，进入新一轮的起舞风速计算及适应度评估;

5）若遗传算法的计算满足迭代终止条件，则输出最优阻尼器参数结果。

2 电涡流TTMD

2.1 电涡流TTMD设计

本文提出一种新型TTMD，利用电涡流原理提供可调节的线性阻尼，如图4所示。TTMD内部的铜环作为质量元件，连接铜环与外壳的扭转弹簧作为弹性元件，铜环与外壳上永磁体的相对运动所产生的电涡流力作为阻尼力。

TTMD的扭转向自振圆频率为

式中 为铜环转动惯量，为铜环半径，为铜环质量，为扭转弹簧刚度。

由电涡流阻尼力产生的扭转向阻尼比为

式中 cd为扭转向阻尼系数。通过控制永磁体的设计参数，即可实现所需的电涡流阻尼力、TTMD的扭转阻尼比。

2.2 TTMD相比于TMD适用范围的优势

TMD的优势是其构造简单，在结构控制方面已有较多研究及应用。但竖向TMD的静态伸长量与线路结构的自振频率关系密切，较低的结构频率会造成较大的TMD伸长量。对于单跨线路的面内频率，可依据下式进行估算[17]

式中 ω为导线频率，g为为重力加速度，EA为导线轴向刚度，H为导线张力。

假定TMD的自振频率与线路频率一致，则竖向悬挂条件下其静态伸长量为

以D型覆冰的LGJ?500/45型号导线为例，计算可得TMD静态伸长量与张力比、线路档距的关系，如图5所示。张力比为导线张力与额定拉断力之比，相关计算参数取值参见文献[13]。

由图5可知，当导线档距大于500 m时，由阻尼器自重引起的阻尼器静态伸长量可达3 m以上。随着档距增加，静态伸长量更大，到档距800 m时可以达到8 m以上，这极大地限制了TMD在大档距线路中的应用。

TTMD运行空间要求小，不存在自重引起的形变，能够普遍适用于各种档距的多分裂线路舞动的防治，尤其可以应用于TMD不再适用的大档距线路。

3 计算设置

3.1 线路参数

選取特高压工程常用的单跨八分裂导线，子导线型号选用LGJ?500/45。该档导线跨度为500 m，两端支座高差为0。假设导线D型覆冰，通过刚性模型天平测力风洞试验获得覆冰八分裂导线气动力系数，其Den Hartog系数和Nigol系数如图6所示。该覆冰八分裂导线的线密度为23.76 kg/m，分裂间距为0.52 m，平动阻尼比为0.44%，转动阻尼比为1.42%，其余相关参数参见文献[13]。选取20阶作为全局形函数，计算得到导线前9阶模态频率如表1所示。

3.2 计算参数

本文针对单个TTMD研究其频率比、阻尼比、质量比、安装位置、导线张力、覆冰质量等参数对覆冰导线起舞风速的影响。其中，频率比、阻尼比属于实际值易偏离设计值的阻尼器参数;质量比、安装位置属于设计阶段确定后实际中不易发生改变的阻尼器参数;导线张力、覆冰质量属于实际值易偏离设计值的导线参数。

质量比（μ）定义为TTMD转动惯量与导线一阶模态转动惯量之比。假定TTMD中铜环半径为0.45 m，当TTMD质量比取0.02时，计算可得TTMD中铜环质量约为165 kg，占多分裂导线总质量的1.4%，对线路动力特性的影响可忽略。文献[18]规定不论档距大小平均运行张力上限为拉断力的25%。假定覆冰前张力比为0.25，由式（1）计算可得覆冰后张力比为0.4。本文取默认的覆冰导线张力比为0.4。

实际观冰监测表明，0°?40°覆冰偏角包含了可能的导线覆冰偏角工况。因此，本文选取0°?40°覆冰偏角进行计算，覆冰偏角间隔为1°。分别选取4阶、20阶全局形函数，对0°?40o覆冰偏角下导线起舞风速进行计算，结果表明在所有覆冰偏角下二者的起舞風速相差均不超过0.2 m/s。在后续遗传算法优化计算中，为提高计算效率并兼顾计算精度，选取4阶全局形函数参与计算。

式（9）的约束条件中，遗传算法所用变量的搜寻范围定义为

遗传算法相关计算参数如表2所示。以质量比0.02为例，TTMD优化计算结果如图7所示。由图可知，遗传代数为10时结果已基本收敛，后续计算中遗传代数均取20。

本文的计算工况如表3所示。工况可分为三类：（a）给定相关参数，优化TTMD参数;（b）给定相关参数，评估控制效果对TTMD参数的鲁棒性;（c）给定TTMD最优参数，研究结构参数不确定性对控制效果的影响。

4 结果分析

4.1 控制效果验证

根据李雅普诺夫第一稳定定理计算可得40°覆冰偏角下起舞风速为11.2 m/s。采用Newmark?β法计算得到40°覆冰偏角、11 m/s和12 m/s风速下导线跨中运动时程如图8所示，由幅值发散情况判断舞动发生情况。结果表明Newmark?β法计算得到的舞动发生情况与李雅普诺夫第一稳定定理计算结果一致，说明了本文方法的正确性。

取质量比0.02，对TTMD的频率比、阻尼比、位置等参数进行优化，所得最优频率比为0.81，最优阻尼比为0.18，最优位置参数为0.39，不同覆冰偏角下起舞风速如图9所示。由图可知，未受控导线的最小起舞风速为4.2 m/s，而TTMD控制下最小起舞风速提高至15 m/s，且大部分覆冰偏角下的起舞风速得到显著提高。这表明TTMD能够有效控制大范围多覆冰偏角下导线的舞动。

4.2 TTMD控制优化结果

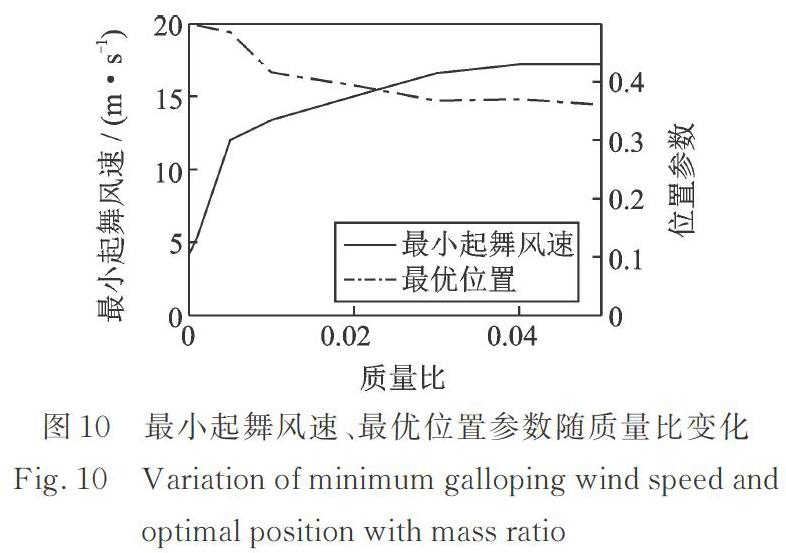
基于不同的质量比，对TTMD的频率比、阻尼比、位置等参数进行优化，所得最小起舞风速及相应的最优位置参数如图10所示。

如图10所示，最小起舞风速随着质量比的增大而持续增大。当质量比为0.005时，最小起舞风速的控制效果已经较为显著，提升了7.8 m/s。当质量比高于0.03时，最小起舞风速的上升趋势不明显。另外，随着质量比的增大，相应的最优位置从跨中逐渐向端部偏移，最后稳定在0.36?0.39的位置参数区间。

分别取质量比0.01，0.02，0.04，沿整档导线取不同安装位置，对TTMD的频率比、阻尼比参数进行优化，结果如图11所示。由于覆冰分裂导线?TTMD系统对跨中位置具有对称性，图中仅展示位置参数0?0.5的部分。如图11所示，在TTMD从线路端部向跨中移动过程中，各质量比条件下的最小起舞风速表现出相似的变化趋势：最小起舞风速首先保持稳定，然后快速增大，并在0.37?0.41位置区间内达到最大值，随后减小。总体而言，在各质量比条件下，TTMD在导线左侧1/4跨?右侧1/4跨（即位置参数0.25至0.75）范围内均能实现良好的起舞风速控制效果。

4.3 TTMD参数鲁棒性分析

分别取质量比0.01，0.02，0.04及相应的最优位置参数，计算TTMD在不同频率比、阻尼比参数下最小起舞风速，结果如图12所示。令质量比为0.02，基于不同的位置参数，计算TTMD在不同频率比、阻尼比参数下最小起舞风速，结果如图13所示。

如图12所示，TTMD的最小起舞风速在频率比、阻尼比参数空间内表现出明显的“尖峰”特征，在尖峰范围内，最小起舞风速维持在较高的水平。质量比0.02条件下，尖峰对应的频率比范围为0.7?0.84，阻尼比范围为0.16?0.3，这就是TTMD能实现良好控制效果的参数范围。随着质量比的增大，最小起舞风速的峰值范围明显扩大，因此提高质量比可以提高TTMD对于舞动风速抑制的鲁棒性。

图13中，在位置参数0.39条件下，最小起舞风速的最大值为15 m/s，在3个位置中表现最优，且TTMD表现出较强的鲁棒性。比较位置参数0.3，0.5可知，二者最小起舞风速的尖峰值较为接近，而位置参数0.5的尖峰明显更宽，TTMD鲁棒性更强，这表明同等起舞风速控制水平下，TTMD安装在靠近跨中的位置比靠近端部的位置具有更强的鲁棒性。

4.4 结构参数不确定性影响

线路运行过程，导线张力、覆冰质量会有一定变化，偏离优化设计的预设值。为研究导线张力、覆冰质量变动的影响，分别取质量比0.01，0.02和0.04，且基于位置参数0.39与覆冰后张力比0.4，优化得到TTMD最优参数;根据最优参数，分别计算导线张力、覆冰质量变化情况下TTMD对起舞风速的控制效果，结果分别如图14和15所示。

如图14所示，对于未受控导线以及各质量比条件下的受控导线，随着导线张力比增大，其最小起舞风速均呈下降趋势，这表明本文选取覆冰前张力比的上限0.25（覆冰后张力比0.4）是较为安全的。因此，在TTMD的初步设计阶段，应当选取较大的张力条件进行计算。

圖15表明，对于未受控导线以及各质量比条件下的受控导线，随着覆冰质量的增大，最小起舞风速均持续增大。因此，基于较小的覆冰质量条件进行TTMD参数的优化设计是较为安全的选择。

5 结 论

本文针对大档距特高压输电线路舞动防治设计了一种扭转向调谐质量阻尼器（TTMD）。建立整档覆冰导线?TTMD系统的运动方程，采用李亚普诺夫稳定定理求解起舞风速;建立基于遗传算法的TTMD防舞优化设计方法，以大范围多覆冰偏角下导线最小起舞风速为优化目标;以某大档距特高压输电线路覆冰八分裂导线为例，对TTMD各项参数进行优化设计，主要结论如下：

1）TTMD相比于竖向TMD没有竖向行程限制，在大档距特高压线路中的应用具有显著优势。

2）本文提出的TTMD防舞优化设计方法可有效提高大范围多覆冰偏角的导线起舞风速。质量比高于0.005时，TTMD即可实现良好的防舞效果。

3）应用整档导线模型实现了对TTMD安装位置的优化。总体而言，TTMD安装在导线左侧1/4跨?右侧1/4跨范围内任意位置均能实现良好的起舞风速控制效果。

4）TTMD对导线的起舞控制效果具有良好的鲁棒性。

5）在TTMD的设计阶段，应采用较高的导线张力、较小的覆冰质量设定，以得到偏于安全的TTMD参数设计值。

参考文献：

[1] 楼文娟， 余 江， 姜 雄， 等. 覆冰六分裂导线舞动风洞试验及起舞风速研究[J]. 振动工程学报， 2017， 30（2）：280-289.

Lou Wenjuan， Yu Jiang， Jiang Xiong， et al. Wind tunnel test and critical wind speed study for galloping of 6-bundled iced conductors[J]. Journal of Vibration Engineering， 2017， 30（2）：280-289.

[2] Hartog J P D. Transmission line vibration due to sleet [J]. Transactions of the American Institute of Electrical Engineers， 1933， 51（4）：1074-1076.

[3] Nigol O， Buchan P. Conductor galloping part I - Den Hartog mechanism [J]. IEEE Transactions on Power Apparatus & Systems， 1981， PAS-100（2）：699-707.

[4] Yu P， Shah A H， Popplewell N. Inertially coupled galloping of iced conductors [J]. Journal of Applied Mechanics， 1992， 59（1）：140.

[5] 姜 雄， 楼文娟. 三自由度体系覆冰导线舞动激发机理分析的矩阵摄动法[J]. 振动工程学报， 2016，29（6）：1070-1078.

Jiang Xiong， Lou Wenjuan. Matrix perturbation method for analysis of 3 DOF iced transmission line galloping mechanism[J]. Journal of Vibration Engineering， 2016，29（6）：1070-1078.

[6] Xu Z D， Xu L Z， Xu F H. Study on the iced quad-bundle transmission lines incorporated with viscoelastic antigalloping devices [J]. Journal of Dynamic Systems， Measurement， and Control， 2015， 137（6）：061009.

[7] Guo H， Liu B， Yu Y， et al. Galloping suppression of a suspended cable with wind loading by a nonlinear energy sink[J]. Archive of Applied Mechanics， 2017， 87（6）：1007-1018.

[8] 严 波， 胡 景， 周 松， 等. 随机风场中覆冰四分裂导线防舞研究[J]. 振动与冲击， 2011， 30（7）：52-58.

Yan Bo， Hu Jing， Zhou Song， et al. Anti-galloping for an iced quad-bundled conductor in stochastic wind field [J]. Journal of Vibration and Shock， 2011， 30（7）：52-58.

[9] 胡 景， 严 波， 祖正华， 等. 一种新型防舞器及其机理研究[J]. 工程力学， 2011， 28（9）：200-206.

Hu Jing， Yan Bo， Zu Zhenghua， et al. A new anti-galloping device and investigation on its mechanism [J]. Engineering Mechanics， 2011， 28（9）：200-206.

[10] Hervé Pohsié G， Chisari C， Rinaldin G， et al. Application of a translational tuned mass damper designed by means of genetic algorithms on a multistory cross-laminated timber building[J]. Journal of Structural Engineering， 2015， 142（4）： E4015008.

[11] 陈 鑫， 李爱群， 徐庆阳， 等. 基于遗传算法的高耸结构环形TLD满意优化设计[J]. 工程力学， 2016， 33（6）：77-84.

Chen Xin， Li Aiqun， Xu Qingyang， et al. Satisfaction optimum design of ring-shape TLD control for high-rise structure using genetic algorithm [J]. Engineering Mechanics， 2016， 33（6）：77-84.

[12] 刘海英， 张琪昌， 郝淑英. 覆冰四分裂输电线舞动研究[J]. 振动工程学报， 2011，24（3）：19-23.

Liu Haiying， Zhang Qichang， Hao Shuying. A study on galloping for iced quad-bundled conductor[J]. Journal of Vibration Engineering， 2011，24（3）：19-23.

[13] Lou W， Huang C， Huang M， et al. An aerodynamic anti-galloping technique of iced 8-bundled conductors in ultra-high-voltage transmission lines[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2019， 193：103972.

[14] 邵天曉. 架空送电线路的电线力学计算[M]. 北京： 中国电力出版社， 2003.

[15] 陈立群， 刘延柱. 非线性振动[M]. 北京： 高等教育出版社， 2001.

[16] Qin Z， Chen Y， Zhan X， et al. Research on the galloping and anti-galloping of the transmission line [J]. International Journal of Bifurcation and Chaos， 2012， 22（2）：1250038.

[17] Irvine H M. Cable Structures[M]. Cambridge， MA： MIT Press， 1981.

[18] 中国电力企业联合会. GB 50545-2010，110 kV～750 kV架空输电线路设计规范[S].北京：中国计划出版社，2010.

China Electricity Council. GB 50545-2010， Code for design of 110 kV～750 kV overhead transmission line[S]. Beijing： China Planning Press， 2010.

作者简介： 楼文娟（1963-），女，教授。 E-mail： louwj@zju.edu.cn