波形钢腹板抗剪性能的研究
2016-03-11李立峰侯立超孙君翠
李立峰 侯立超 孙君翠
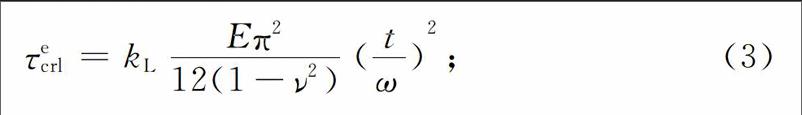

摘 要:为了研究波形钢腹板的抗剪受力性能,首先设计了4根波形钢腹板H型钢梁并进行屈曲加载试验,掌握了波形钢腹板屈曲的基本特征;统计国内外已建波形钢腹板组合桥的波形钢腹板尺寸参数、并对弹性屈曲强度的计算进行了分析,建议了弹性屈曲强度简化计算公式和适用范围;考虑局部弹性屈曲强度要小于整体弹性屈曲强度等参数范围,合理选取一批试验数据对Yi、聂建国等提出的波形钢板非线性剪切屈曲强度计算公式进行了对比分析,并通过ANSYS有限元程序对本文部分试验结果进行了分析验证.结果表明:波形钢腹板主要承担剪力且剪应力沿高度均匀分布;几何初始缺陷对其剪切屈曲强度的影响较明显;在工程应用范围内,文中建议的弹性屈曲强度和非线性剪切屈曲强度公式与试验值和有限元分析值吻合较好,精确度较高,可供工程设计参考.
关键词:钢腹板;抗剪试验;屈曲;弹性;非线性
中图分类号:U448.213 文献标识码:A
文章编号:1674-2974(2015)11-0056-08
波形钢腹板组合桥具有受力明确、截面效率高、桥型美观等诸多优点,彻底解决了混凝土梁桥腹板开裂问题,提高了预应力效率,抗剪屈曲强度高.近年来我国已建成多座该类型桥梁,如较有代表性的山东鄄城黄河大桥、新密溱水桥等.随着波形钢腹板组合桥在我国的大力推广,其设计计算方法需得到逐步的完善,特别是仅承受剪力的薄钢腹板的剪切屈曲问题,包括整体屈曲、局部屈曲及合成屈曲,通过给定的波形如何准确得到其屈曲模态和荷载对指导设计至关重要.
国外学者对波形钢板的抗剪屈曲研究起步于1969年.Easley[1]首先掀起了波形钢腹板梁模型试验研究的序幕,紧接着Elgaaly,Hamilton,Drive,Abbas,Moon,Linder大学[2-6]等多位学者和机构做过波形钢板的剪切屈曲试验;Easley和Skan-Southwell分别给出了波形钢板的整体、局部弹性屈曲强度计算公式,且已得到广泛的认可,但对合成弹性屈曲强度的计算仍存在不同的争议[4,7],考虑非线性等因素后其实际屈曲强度的计算都是基于试验和数值模拟数据的拟合公式.国内研究起步相对较晚,仅周绪红、聂建国、李国强、宋建永[8-10]等人做过类似试验研究和理论分析,其中聂建国[10]做的8根H型钢梁的剪切屈曲试验最具代表性.
相比较而言,对波形钢腹板剪切屈曲的试验探究和理论分析仍需进一步拓展,特别是在波形钢腹板合成弹性屈曲计算上还存在一定异议,其实际非线性屈曲强度的计算公式拟合时采用的数据范围较广,有些并不符合已建波形钢腹板PC组合梁的情况,因此有必要根据已建实桥的主要参数范围,选择尽可能合理的试验数据对相关计算公式做进一步对比分析.
本文首先完成4根波形钢腹板H形钢梁的剪切屈曲试验,以掌握波形钢腹板的基本抗剪性能,为进一步研究波形钢腹板抗剪行为提供试验依据,接着根据已建实桥的波形钢腹板的尺寸参数,深入研究弹性和非线性屈曲强度,并建议相应的计算公式.
1 试验探究
1.1 模型设计
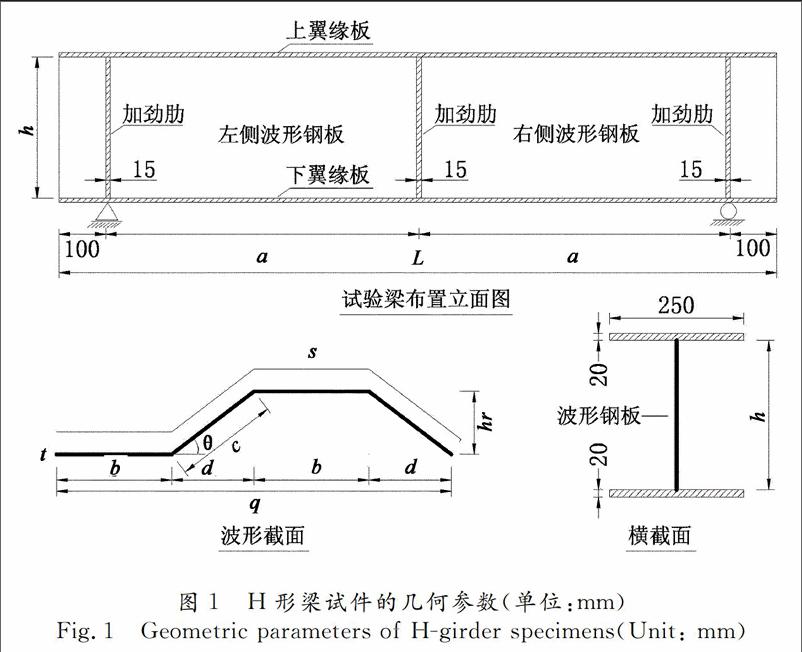
本文首先设计了4片波形钢腹板H形钢梁进行屈曲荷载试验,其设计原则是:①保证模型发生剪切屈曲破坏而不发生其他形式破坏,②L1和L2波形较疏,易发生局部屈曲破坏;G1,G2波形较密,易发生整体屈曲破坏.模型尺寸如图1和表1所示.实测钢腹板的屈服强度平均值为380.2 MPa,极限强度平均值为456.6 MPa.试件制作效果G2如图2(a)所示.
1.2 加载与测试
试验加载装置如图2(b)所示,试验为跨中单调静力加载试验,每级荷载控制在10 kN左右,钢腹板屈曲后采用跨中竖向位移控制加载.
试验前对钢腹板的初始缺陷进行测量,结果如下:试件L1,L2左右两侧腹板初始缺陷最大值分别为1.02 mm和1.09 mm,1.62 mm和1.86 mm,而试件G1,G2分别为1.98 mm和2.06 mm,2.36 mm和2.09 mm,其中L2左侧钢腹板侧向几何初始缺陷分布如图3所示.
试验测试内容主要包括:1)钢腹板的剪应变,采用在腹板表面粘贴应变花的方式;同时在上下翼缘板适当布置应变片以测量弯曲应变;2)跨中竖向变形,在跨中截面布置百分表测试;3)腹板的侧向变形,在腹板沿横向设置百分表.图4为L1和L2的测点布置,试件G1和G2的测点布置基本相同,沿竖向设5个应变花.
1.3 试验过程及破坏现象
根据以上加载和测试方案对4个模型进行了加载测试,结果如下.
1.3.1 试件L1和L2——局部屈曲
试验过程:试件L1左右两侧腹板几乎同时在跨中的波折段发生屈曲破坏;试件L2右侧钢腹板几个子波折段首先发生屈曲破坏,试件整体承载力下降,卸载后,由于左侧钢腹板没有发生破坏,故在右半跨上下翼缘板焊接45°钢板提供斜向支撑,进行第二次加载试验.
破坏现象:两个试件钢腹板的屈曲破坏现象和模式相同,首先在靠近跨中的单个波折段上沿45°发生屈曲破坏,随着加载的继续,多个破坏区域沿45°方向扩展到临近的2~3个子板上,最终破坏形态如图5(a)所示.因此可以判断,试件L1和L2的钢腹板首先发生局部屈曲破坏,随着加载继续,伴随合成屈曲.
1.3.2 试件G1和G2—整体屈曲
试验过程:当加载一定程度后,试件G1左右两侧腹板基本同时发生屈曲破坏;试件G2的左侧腹板首先发生屈曲破坏,卸载后,由于G2的右侧腹板没有发生屈曲破坏,因此按照试件L2的做法进行处理并进行了第二次加载试验.
破坏现象:G1和G2的破坏现象和模式相同,先在腹板中间贯穿多个子板区域发生成45°的屈曲破坏,随着加载的继续,屈曲沿着45°向两侧发展,形成了3个大的破坏区域,平面外的变形加大,其破坏形态如图5(b)所示.因此可以判断,两试件腹板都发生了整体屈曲破坏.
1.4 试验结果及分析
1.4.1 钢腹板剪应变
图6给出了部分钢腹板在屈曲前的剪应变分布情况,其他测点规律基本一致.图6结果表明:波形钢腹板沿高度方向的剪应变分布均匀,且随着荷载线性递增而线性增加.
1.4.2 钢腹板主应变方向
根据腹板每个测点的3个方向应变值计算其主应变方向.限于篇幅,表2给出了部分试件测点的主应变方向.结果表明,钢腹板发生屈曲前,所有测点处主应变方向基本接近45°,因此,波形钢腹板基本处于纯剪状态,只承担剪力.
1.4.3 荷载位移曲线
试件L1和L2的跨中荷载位移曲线如图7(a)所示,由图可以看出,两试件在钢腹板屈曲后承载力突然下降.试件L2的第一次试验的承载力要明显小于第二次试验,即试件L2的左侧钢腹板的抗剪屈曲强度要大于右侧钢腹板的抗剪屈曲强度,这主要是由于实际测得的右侧钢腹板的初始缺陷值相对较大.给出第二次试验L2左侧腹板测点5的侧向荷载位移曲线如图8所示.
试件G1和G2的跨中荷载位移曲线如图7(b)所示,由图可以看出,两试件在钢腹板屈曲后承载力也发生了突然下降.同样由于G2左侧钢腹板的初始缺陷值要大于右侧钢腹板,因此,试件G2的第一次试验的承载力要明显小于第二次试验.给出第二次试验G2右侧腹板测点6的侧向荷载位移曲线如图8所示.
1.5 评 述
综合上述试验研究可知,波形较密时易发生整体屈曲,波形较疏时易发生局部屈曲,有时伴随合成屈曲;波形钢腹板在弹性范围内处于纯剪状态且剪力沿高度方向均匀分布;几何初始缺陷越大对其抗剪屈曲强度影响越大,实际钢腹板的抗剪屈曲强度往往达不到理想的状态.
通过试验对波形钢腹板的抗剪屈曲特性有了宏观认识,但如何根据波形尺寸较为准确地计算分析出其屈曲模态和实际屈曲荷载更为关键.国内外的学者对其实际屈曲强度即非线性屈曲强度的计算都
2 弹性屈曲强度分析
2.1 概 述
国外对波形钢腹板的研究起步于其弹性屈曲强度的研究,包括整体弹性屈曲强度和局部弹性屈曲强度,及合成弹性屈曲强度.目前,对前两者的计算已有了较明确的计算公式,但合成弹性屈曲的理论和计算仍存在不同的看法.波形钢腹板的屈曲模态和屈曲强度与其波形尺寸密切相关,因此有必要对国内外一些已建波形钢腹板组合实桥的波形尺寸参数做出整理归纳,以便下面的进一步分析.随机选取国内外较为代表性的10座波形钢腹板组合桥如表3所示,波形尺寸一并列出.
进一步分析整体屈曲系数如下:由于整体屈曲程度高,不控制波形钢腹板组合梁钢腹板的抗剪设计(后面会进一步分析说明),因此可以从相对保守的角度计算分析.式(6)中β是与边界条件有关的系数,这里按照四边简支的情况取值为1,η是波形钢板桥轴向与波形钢板展开长度的比值,由前面实桥波形参数计算可知其折角θ一般在30°~45°之间,而且国外Linder[6]建议θ≥30°,从实桥设计角度来看θ也不会过大,因此η取值在0.85~0.94之间,且对屈曲系数值影响很小,这里为了设计方便而取定值为0.9,进一步整理式(6)得到式(7)为整体屈曲系数的简化计算公式.因此,对常规波形钢腹板实
桥整体弹性屈曲强度按照式(5),式(7)计算即可.
2.4 对比分析
已有研究表明,合成弹性屈曲强度与局部弹性屈曲强度和整体弹性屈曲强度有关[4,7].按照前面两者计算公式的分析,对前面10座波形钢腹板组合桥的局部和整体弹性屈曲强度计算,结果列于表4中,所有计算结果趋势完全一样,两者强度值均远大于钢材的屈服强度,且局部弹性屈曲强度都小于整体弹性屈曲强度,多数桥两者的比值相差较大,如Cognac桥、三道河中桥和大堰河桥,比值仅在0.25左右.并对其他多座已建实桥整体、局部弹性屈曲强度计算,结果趋势和上面10座桥完全一致.
国内聂建国[10]等人发现波形钢腹板梁的承载力在钢腹板发生局部屈曲后还有一定程度的增长,本文试验试件L1和L2第二次试验的跨中荷载位移曲线也可以看出此趋势.再者,波形较疏时美感更强,而且波形较疏时材料的利用程度更高.因此,从实际波形钢腹板组合桥设计角度考虑,在这里设定由局部弹性屈曲强度要小于整体弹性屈曲强度,且比值最好在0.5以下.
2.5 合成弹性屈曲强度
合成屈曲是一种介于局部屈曲和整体屈曲之间较为复杂的屈曲形式,其理论和计算仍没有一致确定的结论.国外对其研究最初是基于局部弹性屈曲强度、整体弹性强度及钢材的剪切屈服强度[4,7];后来Yi等人又认为合成屈曲与钢材的屈服强度没有关系,如式(8)所示.对于n的取值,不同的学者有不同的看法,主要有1,2,4等几个取值.本文采用Yi等人的结论,不考虑钢材本身的屈服强度,用式(8)计算合成弹性屈曲强度,并进一步分析确认n取值为1的合理性.
由公式本身可以看出,合成弹性屈曲强度是小于整体和局部弹性屈曲强度的,且与两者的大小关系相关.而实际波形钢腹板组合桥中,局部弹性屈曲强度是小于整体弹性屈曲强度的.因此,本文仅在该范围内分析.
由图11可以看出,在上述给定的参数范围内,当局部弹性屈曲强度小于整体弹性屈曲强度时,按照公式(9)计算出的弹性屈曲强度和有限元分析结果趋势是一致的,而且在保守的基础上是较为接近的.从实桥设计角度考虑,hr/t取值在10~20时按照公式(9)计算合成弹性屈曲强度更为安全保守.
3 非线性屈曲强度分析
3.1 试验对比分析
波形钢板的弹性屈曲强度大于钢材本身的剪切屈服强度时,就需要考虑非线性等因素的影响,即钢腹板的非线性屈曲强度.国内外学者在数值拟合及试验验证的基础上给出了多种计算公式,但所取数值较为广泛,有些并不符合波形钢腹板组合桥的实际情况,因此有必要做进一步的整理分析.由于受到初始缺陷、残余应力、边界条件、施工制作误差等诸多不确定的因素影响,波形钢板非线性屈曲强度的计算很难达到一定精确度,只能在保守的情况下尽量减少误差.
本文选取较为合理的Yi[7]的计算公式(10)和国内聂建国[10]的计算公式(11)进行研究分析,并根据前文对实际波形钢腹板PC组合桥参数分析,按照以下原则筛选了包括本文试验在内的4组试验数据:①ω/h≤0.3;②a/h≥1;③折角θ在30°~45°之间;④局部弹性屈曲强度要小于整体弹性屈曲强度.
由图12可以看出,剪切屈曲长细比小于1时,聂给出的计算公式更为保守,当剪切屈曲长细比在1和2之间时,两者曲线非常的接近.所选取的试验数据较好地分布于两曲线周围,离散性较低,仅有个别试验点稍低于曲线.因此在进一步选择的合适试验数据范围内,Yi和文献\[10\]给出的计算公式都能很好地计算出考虑非线性后波形钢腹板的实际剪切屈曲强度,在保守的基础上也比较准确,适合设计计算参考使用.
3.2 有限元分析
本文采用有限元程序Ansys14.0对试件L1, L2建立了有限元模型,进行了特征值弹性屈曲分析和非线性屈曲分析.与前面分析合成弹性屈曲强度建模一样,用shell181单元模拟波形钢腹板,其中试件L2波形钢板的有限元模型如图13所示.考虑钢腹板承担全部剪力[2,10]且沿高度均匀分布,按照本文建议的弹性屈曲强度的公式计算试件L1,L2的值分别为97.6 MPa, 124.8 MPa,有限元计算结果分别为106.8 MPa, 135.2 MPa,结果吻合相对较好.对于钢腹板非线性屈曲强度,考虑几何非线性和材料非线性,并按照实际施加了初始缺陷,其中L1侧向荷载位移曲线如图14所示,与L1试验梁一侧剪力(加载力的一半)较接近,且破坏强度远小于钢材本身的剪切屈服强度τ.y,发生了屈曲稳定破坏形态,将L1和L2试验值、有限元计算值、按照文献\[10\]计算理论值列于表5中,其中试件L2以左侧钢腹板为准.由表5可以看出,有限元分析由于没有考虑残余应力等其他因素情况下计算值略大,本文建议的钢腹板非线性屈曲强度的计算公式与试验及有限元分析结果吻合较好,误差在5%以内,在保守的基础上相对精确.
4 结 论
1)通过4根波形钢腹板H形钢梁的抗剪屈曲静力试验,初步掌握了其抗剪性能.试验结果表明:波形钢腹板基本处于纯剪状态,且剪力沿高度方向均匀分布;初始缺陷越大对其非线性屈曲强度的影响越大.
2)根据分析实桥波形钢腹板波形参数,对局部弹性屈曲系数可以直接取值5.34,并对整体屈曲系数给出了较为方便的建议公式.计算的实桥局部弹性屈曲强度小于甚至远小于整体弹性屈曲强度,在此基础上对合成弹性屈曲强度进行了分析,结果显示在给定的范围内,本文建议的弹性合成屈曲强度计算公式在保守的基础上有相对较高的精度.
3)根据前文分析,选取了包括本文在内的4组实验数据,选取时按照以下原则:①ω/h≤0.3;②a/h≥1;③折角θ在30°~45°之间;④按照前面的计算公式算出的局部弹性屈曲强度要小于整体弹性屈曲强度.通过选取的数据对聂建国等人及Yi等人给出的波形钢腹板实际非线性屈曲强度计算公式进行对比分析,并建立本文试验梁的有限元模型分析对比.三者数值吻合较好,建议的计算公式在相对保守的基础上精确度较高,可供工程设计参考.
参考文献
[1] EASLEY J T, MCFARLAND D E. Bucking of light-gage corrugated metal shear diaphragms\[J\]. Journal of the Structural Division, ASCE, 1969,95:1497-1516.
[2] ELGAALY M,HAMILTON R, SESHADRI A.Shear strength of beams with corrugated webs\[J\].Journal of Structural Engineering, ASCE, 1996,122(4):390-398.
[3] DRIVE R G, ABBAS H H, SAUSE R. Shear behavior of corrugated web bridge girders \[J\].Journal of Structural Engineering,2006, 132(2):195-203.
[4] ABBAS H H, SAUSE R, DRIVE R G. Shear strength and ability of high performance steel corrugated web girders\[C\]//Proceedings of the structural stability research council annual technical session, 2002: 361-387.
[5] JIHO Moon, JONGWON YI, BYUNG H CHOI, et al. Shear strength and design of trapeziodally corrugated steel webs\[J\].Journal of Constructional Steel Research,2011,67(2):223-236.
[6] LINDER J, HUANG B. Beulwerte für trapezfrrmig profilierte bleche unter schubbeanspruchung[J].Stahlbau,1995,64(2):370-374.(In Germany)
[7] YI J, GIL H, YOUM K, et al. Interactive strength of trapezoidally corrugated webs\[J\]. Eng Struct, 2008, 30:1659-1666.
[8] 李国强,张哲,孙飞飞. 波纹腹板H型钢梁抗剪承载力\[J\].同济大学学报,2009, 37(6):709-714.
LI Guo-qiang, ZHANG Zhe, SUN Fei-fei. Shear strength of H-beam with corrugated webs\[J\]. Journal of Tongji University, 2009,37(6):709-714. (In Chinese)
[9] 周绪红,孔祥福. 波纹钢腹板组合箱梁的抗剪受力性能\[J\].中国公路学报,2007,20(2):77-82.
ZHOU Xu-hong, KONG Xiang-fu. Shear mechanical property of composite box girder with corrugated steel webs\[J\]. China Journal of Highway and Transport, 2007,20(2):77-82. (In Chinese)
[10] 聂建国,朱力, 唐亮.波形钢腹板的抗剪强度\[J\].土木工程学报,2013,46(6):97-109.
NIE Jian-guo, ZHU Li, TANG Liang. Shear strength of trapezoidal corrugated steel webs\[J\]. China Civil Engineering Journal, 2013,46(6):97-109. (In Chinese)
