周边建筑对轻轨站房风荷载的干扰效应研究

李晨 李波 陈金科 郭坤鹏

摘要： 以典型轻轨站房为例，利用刚性模型测压风洞试验，研究了周边建筑与站房高度比分别为0.66，1.08，1.50条件下，周边建筑对轻轨站房风荷载的干扰效应。风洞试验结果表明，受周边建筑物干扰效应影响，站房受到的水平风荷载减小，当周边建筑物高度不高于站房（高度比=0.66，1.08）时，竖向风荷载亦减小;当周边建筑物高于站房（高度比=1.5）时，在0°?70°风向区间站房收到的竖向风荷载增大。周围建筑物使得站房周边流场中的湍流成分增加，作用于站房表面的脉动风压亦增大，当周边建筑物高于站房时，脉动风荷载的干扰效应尤为明显，水平向脉动风荷载干扰系数达到1.8。站房表面极值风压受周边建筑影响较大，尤其是当施扰建筑高度大于站房时，该种情况下，屋盖及墙面极值风压均明显增大，其中，屋盖角区风吸力增大12.5%，墙面角区风压力和风吸力增幅分别达到33.5%和16.7%。

关键词： 风荷载; 风洞试验; 轻轨站房; 干扰效应; 干扰因子

中图分类号： TU311.3; TU312+.1 文献标志码： A 文章编号： 1004-4523（2021）05-0943-08

DOI：10.16385/j.cnki.issn.1004-4523.2021.05.007

引 言

近年来，为方便人们出行，尽早完成公共交通网络化进程，轻轨修建数量逐年增加。站房是轻轨标志性建筑，为了满足功能及地标性特征，常常采用大跨空间钢结构，该种结构体系柔度大、重量轻、阻尼小，是典型的风敏感结构[1?3]。针对这一特点，国内外学者通过风洞试验得到了采用大跨空间站房风荷载分布特性，并通过风振响应分析给出了该类结构风振响应及等效静力风荷载[4?6]。需要注意的是，轻轨站房周边环境复杂，必须考虑周围建筑物的风致干扰效应。Hui等[7]、Kim等[8?9]、Mara等[10]、Lam[11]针对高层建筑的风致干扰效应进行了相关研究，指出风致干扰效应会对结构风荷载分布产生较大影响，风致干扰效应不可忽视。但以上研究主要针对高层建筑的干扰效应，对于大跨度结构的风致干扰效应研究有所欠缺，李波等[12]利用多通道同步测压实验，研究了周边高层建筑对大跨度空间结构风荷载的干扰效应。研究表明，受到周边建筑影响，来流流场以及湍流成分改变，导致作用于大跨度空间结构的平均风荷载、脉动风荷载发生改变。Chen [13]研究了周边高层建筑与低矮建筑间距、建筑物高度比、风向等因素下，低矮建筑受到的干扰效应，研究表明，周边建筑高度增加，或减小建筑物间距会导致屋盖上风压增大。可见，在大跨度空间结构主体结构、围护结构抗风设计过程中，必须考虑周边建筑的干扰效应。值得注意的是，目前专门针对轻轨站房的风致干扰效应研究还十分缺乏。

本文以最为典型的、拱形高架轻轨站房为例，通过刚性模型测压风洞试验，研究了周围建筑对轻轨站房风荷载的干扰效应，为该类结构抗风设计提供重要参考。

1 风洞试验概况

1.1 试验风场

1.2 试验模型及工况设计

某典型拱形高架轻轨站房纵向长度为97 m，跨度=28 m，屋盖最高处高度=19.5 m，纵墙与屋盖相连组合成整体网壳结构（如图2所示）。该线路轻轨站房周围有大量的周边建筑，且周边建筑的高度和体量各不相同。

本次试验模型几何缩尺比选为1∶100，最大阻塞率为3%。试验模型为刚性模型，试验模型采用ABS材料制作，主体模型具有足够的强度和刚度。周边建筑利用由密度板材料制作的长方体模型进行模拟（如图3所示）。

为了研究周边建筑对轻轨站房表面风压的影响，试验根据轻轨站房所处环境，设计了单体工况和6个干扰工况的测压风洞试验。施扰模型尺寸为13 cm×21 cm×30 cm，试验过程中，利用不同布置方式，分为三类高度比干擾情况，三种高度比/H分别为0.66，1.08，1.50，并且在各高度比条件下，施扰建筑分为单、双侧布置两种情况。结合轻轨站房一般性路况，设计周边建筑与试验模型相距为25 cm。另外，本文参考Tamura[15]采用的建筑面积密度概念，利用线面积密度对施扰建筑进行描述，确定方式如下：周边建筑总宽度与站房长度的比值。各干扰工况信息如表1所示。

试验中，首先进行单体工况测压试验，然后进行考虑周边建筑干扰效应的测压试验。屋盖及两侧墙体外表面共布置170个测点，屋盖内表面布置51个测点，采样频率312.5 Hz，每个通道连续采样20000次，采样时间64 s，测量得到的风压按照文献[16]的方法进行管道修正。

1.3 试验数据处理方法

为方便比较，建筑表面的风压通常采用对应于参考点的无量纲风压系数表示[17]。

将站房表面风压按水平向、竖直向进行合成，水平向、竖直向风荷载，并通过下式计算水平向、竖直向风力系数，以描述作用于主体结构的风荷载特征。

式中 ，分别为水平向、竖直向风力系数;为测点风压系数;为测压点所代表的特征面积;为测点代表的特征面的法向与水平向夹角。

本文采用干扰因子来衡量周边建筑对站房表面风压的影响程度，其中平均风荷载、脉动风荷载的干扰因子分别用，表示[17]：

考虑到风压的非高斯特征，利用Hermite矩模型理论[19]，计算测点风压系数的峰值因子和极值风压。

2 平均风荷载特征

下面将根据风洞试验结果，分析周边建筑对站房平均风荷载的干扰效应。

2.1 平均风压

图4给出0°风向角下，单体工况、上游施扰（工况D?1.50，180°风向角）、下游施扰（工况D?1.50）、双侧施扰（工况S?1.50）的平均风压系数分布图。

可以看出，单体工况下，平均风压对称性较好，除迎风侧立面是正压外，顶面和背风侧立面均为负压区;站房顶面边缘处出现流体分离，风吸力较大，风压系数达到-1.5，背风侧立面风吸力很小，其值仅为-0.3左右。上游施扰时，站房受施扰建筑遮挡影响，顶面负压减小，迎风侧立面由风压力变为风吸力，风压系数达到-0.4。下游单侧干扰时，顶面区域风吸力减小到-1.0左右，背风面因下游建筑阻塞效应产生的回流，使得立面风吸力减小，同时底部区域由风吸力变为风压力。双侧施扰时，站房顶面与背风面风吸力均明显减小，迎风面分布形式与上游单侧工况相似。

综上，站房周边存在干扰建筑时，立面风压受“遮挡”效应影响，风压减小甚至变号，对于屋盖顶面，当施扰建筑起“遮挡”作用时，风压减小，无“遮挡”作用时，流体分离产生的旋涡会使风压增大。

2.2 平均风力系数及干扰因子

图5给出了站房水平向风力系数随风向角变化曲线。

可以看出，单体工况下，当风向角为0°?20°时，风力系数逐渐增大;随风向角度数继续增加，平均风力系数减小，90°风向角时，风力系数几乎为0;风向角为90°?180°的风力系数与0°?90°呈反对称分布。干扰工况下，站房水平向平均风力系数均小于单体工况，单侧干扰时，风力系数曲线变化规律与单体工况相近，双侧干扰时，风力系数曲线关于90°呈反对称分布。

图6给出0°风向角下水平向风力系数的干扰因子。建筑高度低于站房环境下，下游施扰时，干扰效应较小，干扰系数接近1，而上游及双侧施扰时，施扰建筑起“遮挡”效应，干扰系数在0.3左右;施扰建筑高度与站房相近环境下，下游施扰时，平均风力干扰系数降为0.73，上游与双侧施扰时，干扰系数仍在0.3左右;施扰建筑高于站房环境下，下游施扰时，平均风力干扰系数降为0.64，上游与双侧施扰时，干扰系数仍为0.3左右。

图7给出竖直向平均风力系数随风向角的变化曲线。可以看出，在单体工况下，竖直向平均风力系数曲线关于90°呈对称分布;0°风向角下，风力系數达到最大值-0.96，随着风向角增大，风力系数减小;90°风向角下达到最小值，为-0.14。在干扰工况下，当风向角为0°?70°时，除D?1.50工况外，竖直向平均风力系数均大于单体工况，风吸力较小;当风向角为70°?130°时，各干扰工况竖直向平均风力系数值小于单体工况，风吸力明显增大。风向角大于130°时，干扰规律与0°?70°基本相同。

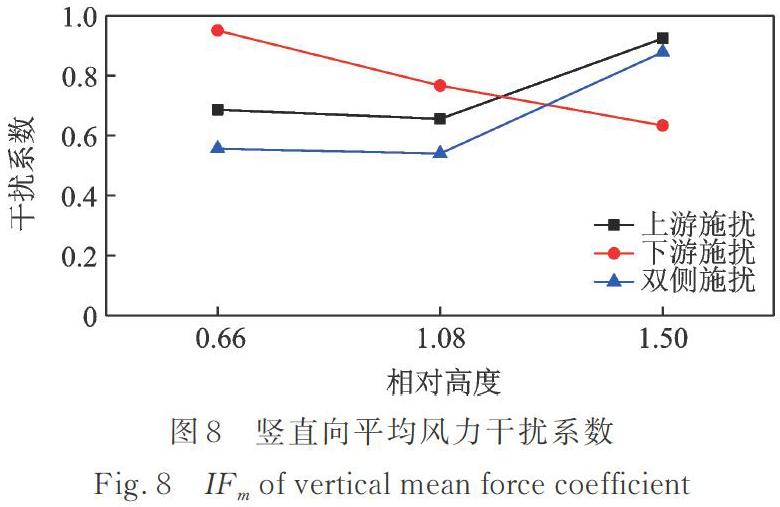
图8给出了0°风向角时竖直向平均风力系数干扰因子。可以看出，施扰建筑高度低于站房环境下，下游施扰时，竖直向风力系数与单体工况基本相同;而上游及双侧施扰时，施扰建筑改变来流，竖直向风力系数有所减小。施扰建筑高度与站房相近环境下，下游施扰时，平均风力干扰系数为0.76;上游与双侧施扰时，干扰系数略低于郊区环境。施扰建筑高于站房环境下，下游施扰时，施扰建筑阻塞效应产生回流，使得竖向平均风力明显减小;上游及双侧施扰时，施扰建筑对站房产生的“遮挡”效应使得风力系数有所减小，干扰系数分别为0.92，0.88。

3 脉动风荷载特征

3.1 脉动风压

图9给出高度比为1.50工况下，0°风向角时，单体工况、上游施扰（工况D?1.50，180°风向角）、下游施扰（工况D?1.50）、双侧施扰（工况S?1.50）下的脉动风压系数分布图。

可以看出，单体工况下，脉动风压系数分布具有一定的对称性，顶面来流前缘部分根方差较大，达到0.25，其他区域有所减小，根方差降低为0.2。上游施扰时，由于施扰建筑的“遮挡”效应，增大来流中湍流成分，导致迎风侧立面脉动风压系数增大，风压系数根方差达到0.40;立面处于施扰建筑间隙的区域受“穿堂风”效应影响，脉动风压系数增大到0.45。下游施扰时，迎风面及顶面脉动风压系数变化较小，背风面受下游建筑影响，脉动风压系数增大到0.25。在双侧施扰时，迎风面及顶面脉动风压明显增大，其脉动风压系数略大于上游施扰工况。

3.2 脉动风力系数及干扰因子

图10给出水平向、竖直向脉动风力系数随风向角的变化曲线。可以看出，单体工况下，水平向脉动风力系数随着风向角增大呈先减小后增大趋势，且曲线关于90°对称分布，当风向角为0°时，脉动风力系数达到最大，为0.2。高度比为0.66，1.08时，站房水平向脉动风压系数趋势与单体工况相似，脉动风力系数受干扰较小;在高度比为1.50时，位于施扰建筑间隙的下游区域受到“穿堂风”效应影响，脉动风力系数明显增大。对于竖直向脉动风力系数，高度比为0.66，1.08工况下，脉动风压系数与单体工况相近;高度比为1.50工况下，双侧施扰时，竖直向脉动风力系数在各风向角下均明显增大，而单侧施扰时，风向角0°?100°范围内，脉动风力系数与单体工况相近，风向角110°?180°时，风力系数显著增大。

可以看出，对于水平向脉动风力干扰系数，当施扰建筑高度接近和小于站房环境下，施扰建筑改变站房周边流场环境，脉动风力系数有所增;当施扰建筑高度高于站房时，上游和双侧施扰时，脉动风力系数受扰动明显，干扰因子分别达到1.79，1.66。对于竖直向脉动风力系数，施扰建筑高度小于站房时，脉动风力系数基本不受施扰建筑影响;高度相接近时，上游和双侧施扰时，脉动风力增大，干扰系数达到1.2左右;高度大于站房工况时，在上游和双侧施扰情况下，施扰建筑高度远大于站房高度，流场改变很大，导致脉动风力系数明显增大，干扰系数达到1.4。

4 极值风荷载特征

4.1 极值风压

图12给出36个风向角下，站房在各工况下最不利风压系数极小值分布图。从图中可以看出，单体工况下，屋盖边缘极小值风压系数较大，中部区域有所减小，极小值风压系数为-2.0;在工况S?1.50下，屋盖边缘极小值风压系数增大，达到-2.5，位于施扰建筑附近的部分区域极小值风压系数变化幅度较大，达到-3.0。

4.2 分区极值风压系数及干扰系数

表2给出了墙面和屋盖特征分区极值风压系数，其中，屋盖和墙面根据规范分为边区、角区和中区，如图13所示。可以看出，施扰建筑高度小于站房时，墙面边区极值变化较小，屋面边区2风压系数极大值明显增大，其他屋面极值风压系数均减小;当施扰建筑高度与站房相近时，墙面边区风压系数极小值增大，屋盖边区2极大值明显增大，其他区域极值受施扰建筑影响减小;当施扰建筑高度大于站房时，墙面角区、边区极小值增大，屋盖各区极值风压系数变化较小。

圖14给出了极值风压最大的屋盖和墙面角区极值风压系数对比柱状图。屋盖角区，风压系数极大值受施扰建筑影响较小，各干扰工况下，风压系数极大值均减小;风压系数极小值在单侧干扰工况下减小，双侧干扰工况下风压系数极小值增大12.5%。墙面角区，施扰建筑高度大于站房时，墙面角区极大值明显增大，增幅达33.5%以上，其他工况增幅在10%以内;风压系数极小值受周边建筑影响，各干扰工况墙面风压系数极小值增大10%左右。可见，周边建筑对极值风荷载有较大影响，在围护结构设计中，干扰引起的极值风压变化不容忽视。

5 结 论

城市轻轨站房多处于城市楼群中，周围建筑对作用与建筑表面的风荷载的干扰效应显著，本文以典型轻轨站房为例，进行了刚性模型测压风洞试验，针对周边建筑对轻轨站房风荷载的干扰效应进行研究，结论如下：

（1）站房平均风荷载受周边建筑干扰明显。各干扰工况下，水平向平均风荷载减小。当施扰建筑低于或接近站房时，竖直向风荷载有所减小，干扰系数最低达到0.16;当施扰建筑高度大于站房时，竖向风荷载明显增大，而在单侧施扰工况0°?70°时，竖向风荷载减小。

（2）当施扰建筑高度小于或接近站房高度时，水平和竖直向脉动风荷载增大;当施扰建筑高度大于站房高度时，脉动风荷载增大最为明显，其干扰系数达到1.8。

（3）站房表面极值风压受周边建筑影响较大，尤其是当施扰建筑高度大于站房时，该种情况下，屋盖及墙面角区极值风压均明显增大，其中，屋盖角区风吸力增大12.5%，墙面角区风压力和风吸力增幅分别达到33.5%和16.7%。

参考文献：

[1] Holmes J D. Wind Loading of Structures[M]. New York： Spon Press， 2001.

[2] 李元齐， 董石麟. 大跨度网壳结构抗风研究现状[J].工业建筑， 2001， 31（5）： 50-53.

Li Yuanqi， Dong Shilin. Wind-resistant research of large-span reticulated shell structures[J]. Industrial Construction， 2001， 31（5）： 50-53.

[3] Di Wu. Estimation of internal forces in cladding support components due to wind-induced overall behaviors of long-span roof structure[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2015， 142： 15-25.

[4] 柯世堂， 陈少林，葛耀君. 济南奥体馆屋盖结构风振响应和等效静力风荷载[J]. 振动工程学报， 2013， 26（2）： 214-219.

Ke Shitang， Chen Shaolin， Ge Yaojun. Wind-induced response and equivalent static wind load for suspended dome roof structure of Jinan Olympic Sports Hall[J]. Journal of Vibration Engineering， 2013， 26（2）： 214-219.

[5] 陈琳琳， 崔会敏，郑云飞，等. 大跨柱面网壳结构风荷载试验研究[J].工程力学， 2019， 36（Z1）： 189-193.

Chen Linlin， Cui Huimin， Zheng Yunfei， et al. Experimental investigation of wind load on large-span cylindrical latticed shell[J]. Engineering Mechanics， 2019， 36（Z1）： 189-193.

[6] 田玉基， 杨庆山. 大跨度屋盖结构脉动风振响应的振型能量参与系数[J]. 振动工程学报， 2007， 20（3）： 219-223.

Tian Yuji， Yang Qingshan. Mode energy participation factors for fluctuating wind-induced response of large-span roof structure[J]. Journal of Vibration Engineering， 2007， 20（3） ： 219-223.

[7] Hui Y， Tamura Y. Pressure and flow field investigation of interference effects on external pressures between high-rise buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2013， 115： 150-161.

[8] Kim W， Tamura Y. Interference effects on local peak pressures between two buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2011， 99： 584-600.

[9] Kim W， Tamura Y. Interference effects on aerodynamic wind forces between two buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2015， 147： 186-201.

[10] Mara T G， Terry B K. Aerodynamic and peak response interference factors for an upstream square building of identical height[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2014， 133： 200-210.

[11] Lam K M. Interference effects on wind loading of a row of closely spaced tall buildings [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2008， 99：584-600.

[12] 李 波， 杨庆山，冯少华，等. 周边建筑对大跨屋盖风荷载的干扰效应研究[J].实验流体力学， 2010， 26（5）： 27-30.

Li Bo， Yang Qingshan， Feng Shaohua， et al. Research on the interference effect of surrounding buildings on the wind load of long-span roof[J]. Journal of Experiments in Fluid Mechanics， 2010， 26（5）： 27-30.

[13] Chen Bo. Wind interference effects of high-rise building on low-rise building with flat roof[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2018， 183： 88-113.

[14] 中华人民共和国建设部. GB 50009-2012，建筑结构荷载规范[S].北京：中国建筑工业出版社，2012.

Ministry of Construction People's Republic of China. GB 50009-2012， Load code for the design of building structures[S]. Beijing： China Construction Industry Press， 2012.

[15] Tamura Y. The interference effect of surrounding roughness on wind pressures of rectangular prism[C]. The 6th International Colloquium on： Bluff- Bodies Aerodynamics & Application， Milan， Italy， 2008： 1-10.

[16] 陈 波，骆盼育，杨庆山.测压管道系统频响函数及对风效应的影响[J].振动与冲击， 2014， 33（3）： 130-134.

Chen Bo， Luo Panyu， Yang Qingshan. Frequency response function of a pressure measurement pipe system and its effect on structural wind effects[J]. Journal of Vibration and Shock， 2014，33（3）： 130-134.

[17] 李 波， 單文姗，杨庆山，等. 肋条对仿古悬挑屋盖风荷载特性的影响[J].振动工程学报， 2016， 29（2）： 269-275.

Li Bo， Shan Wenshan， Yang Qingshan， et al. Effect of ribs on wind load of archaize cantilever roof[J]. Journal of Vibration Engineering， 2016， 29（2）： 269-275.

[18] Tamura Y. Actual extreme pressure distributions and LRC formula[J]. Journal of Wind Engineering and Industrial Aerodynamics， 2002， 90： 1959-1971.

[19] 李 波，田玉基，杨庆山.非高斯风压时程的矩模型变换与峰值因子计算公式[J].振动工程学报， 2016， 29（3）： 395-402.

Li Bo， Tian Yuji，Yang Qingshan. Moment-based transformation of non-Gaussian wind pressure histories and non-Gaussion peak factor formula[J]. Journal of Vibration Engineering， 2016， 29（3）： 395-402.

作者简介： 李 晨（1990-），男，博士研究生。电话：15901077530; E-mail：lichen_110613@163.com

通讯作者： 李 波（1978-），男，教授。E-mail： libo_77@163.com