从Jaynes-Cummings模型到Rabi模型稳态纠缠的绝热制备

吕东燕,邓瑞浩,周原

(湖北汽车工业学院理学院,湖北 十堰 442002)

0 引言

自从1935年薛定谔猫态这一奇妙的物理概念-量子纠缠问世以来,作为量子信息处理的最基本资源,量子纠缠一直牵动着当今量子信息科技发展的最前沿[1]。一直以来,基于不同的体系和方案来制备高品质的量子纠缠态都是量子光学和量子信息领域最重要的研究课题之一[2,3]。纵观量子纠缠的研究和发展历程,已经涌现诸多杰出的研究成果[4-6]。2000年,Zheng和Guo[7]提出了利用腔QED方案来制备双原子纠缠的理论方案,该理论方案是基于腔QED动力学过程制备量子纠缠的代表性方案,对后续基于腔QED类体系执行量子信息处理具有基础指导意义。近年来,超导技术的蓬勃发展极大地加快了超导类量子纠缠发展的步伐,2017年潘建伟团队和2019年朱诗尧团队利用超导量子电路分别实现了10 bits和20 bits纠缠态的制备和操控[8,9]。虽然利用不同体系来制备纠缠态的方案多种多样,但是在实际的物理体系中制备更高品质的纠缠仍然存在很大的研究空间。基于现有的研究基础提出一些制备纠缠的新的理论方案是一个有趣的问题[10-17]。

本文提出了一种利用基态绝热转化来制备稳态纠缠的新的理论方案。首先,基于Rabi模型和Jaynes-Cummings(JC)模型的基本物理性质,从旋转波近似、本征能量和动力学演化规律这三个方面来比较和阐述这两者之间的异同[10];其次,借鉴参量放大法增强耦合这一物理思想,通过引入二阶非线性驱动,在新的压缩表象下,不仅可以增强原子与光子之间的相干耦合强度,还可以将原有的JC模型转变为有效的Rabi模型;最后,利用本方案构建一个从JC模型到Rabi模型的高效的量子绝热通道,通过该通道可以将初始的原子-光子的非纠缠基态转变为稳定的薛定谔猫态。不仅如此,如果对演化末态的原子进行选择性测量,还可以将光子制备成稳态的奇(偶)相干态。由于其基态绝热性,这一方案将具有更好的抗噪性和可操作性。

1 JC模型和Rabi模型的对比研究

1.1 旋转波近似

考虑一个由二能级原子或者人工原子构建的单个量子比特,其上下能级的量子态定义为基态|g〉和激发态|e〉,能级间隔为ω1。假设单模电磁模式ω2与这个二能级体系发生共振耦合,则系统所满足的哈密顿量可以表示为(取普朗克常量ħ=1)

在相互作用绘景下,(1)式和(2)式分别可以表示为

在共振或者近共振且满足弱耦合的前提条件下(|ω1-ω2|＜g且|ω1+ω2|≫g)两个模型是等价的,且Rabi模型满足旋波近似,退化为更简洁的JC模型。令Δ=ω1-ω2,可得

相反,如果耦合强度满足的是强耦合甚至是超强耦合,即g≈ω1,2或g＞ω1,2,在Rabi模型中的反旋波项不能被忽略,因此

1.2 本征能量比较

从本征能谱的角度也可以比较这两个模型。电磁模式的空间截断且假设电磁场模式的本征矢量被限定在子空间{|n-1〉,|n〉},二能级原子的量子态基矢空间为{|g〉,|e〉}。根据(1)式,对角化哈密顿量HRabi,得到其本征能量为

在相同的基矢空间下对角化HJC,也可以得到其本征能量为

不失一般性,假设Δ=ω1-ω2=0,g/ω1=k,n=10,两种模型的本征能量曲线如图1所示。从图1可以看出,在弱耦合条件下,特别是在耦合强度满足k＜0.2时,如图(b),即图(a)中虚线圆框所标注的区域,Rabi模型和JC模型的本征能量是完全重合的,即在该区域范围JC模型与Rabi模型是完全等价的;随着耦合强度的继续增加,Rabi模型的本征能量曲线与对应的开始出现分离,且随着耦合强度的增加其偏差越来越大,但是与的本征能量曲线始终是重合的,这与(7)和(8)式所计算的结果一致;随着耦合强度进一步增强到强耦合甚至超强耦合区域时,如图(a)所示,当k≥5时,Rabi模型开始出现双重简并现象,即而且始终与这两条简并曲线重合。

图1 Rabi模型和JC模型本征能量曲线比较图。耦合强度变化范围是(a)g/ω1∈[0,10],(b)g/ω1∈[0,1]时的本征能量曲线Fig.1 Comparisons of the Eigen energies between the Rabi model and JC model.Curves for the Eigen energies varying with the coupling strength(a)g/ω1∈ [0,10]and(b)g/ω1∈ [0,1]

1.3 动力学比较

考虑到实际腔量子电动力学(C-QED)理论,综合考虑系统的实际耗散、退相干等不利因素,不管是Rabi模型还是JC模型,都可以用量子主方程来刻画这两个不同的动力学过程,即

系统的初态设为|ψ(0)〉=|0〉|e〉,即原子处于激发态且电磁模式处于真空态,考虑到实际耦合强度的增强过程,两种不同模型的动力学平均值和的演化图样如图2所示,横坐标对应的是时间自由度的演化坐标,纵坐标对应的则是耦合强度这个自由度的变化规律。在弱耦合区域,即k＜1区间,Rabi模型和JC模型的动力学演化规律具有一致性,这充分说明了旋波近似的有效性;但是随着耦合强度的进一步增强,Rabi模型的动力学演化明显区别于JC模型,即Rabi模型的演化过程中,会出现多光子跃迁的现象,然而JC模型的演化则满足单光子共振跃迁。

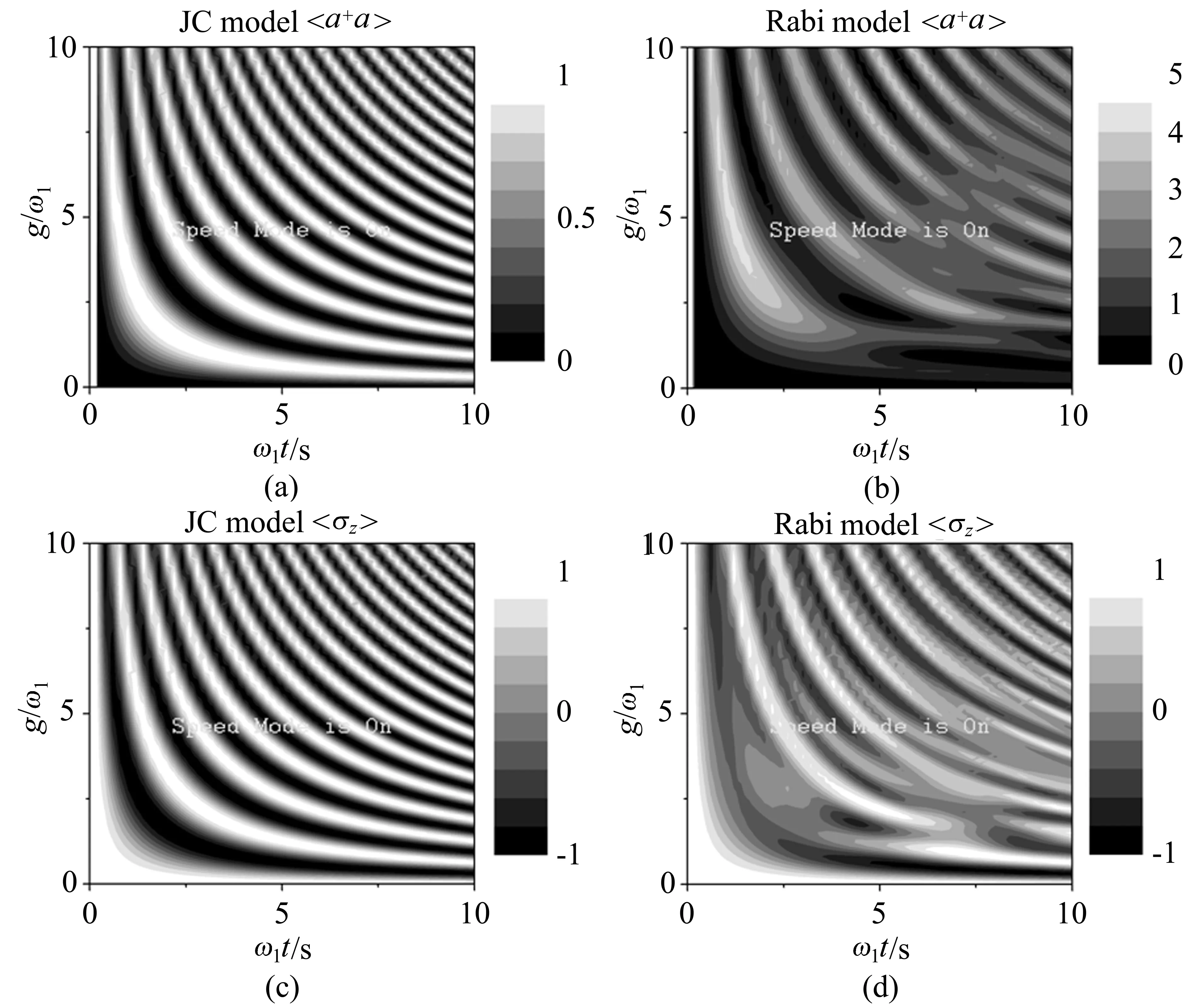
图2 JC模型和Rabi模型的动力学比较图。(a)平均光子数和(c)自旋z方向的平均值在JC模型下的动力学演化规律;(b)平均光子数和(d)自旋z方向的平均值在Rabi模型下的动力学演化规律Fig.2 Dynamical comparison between the JC model and Rabi model.(a)and(c)represent the JC type dynamical averages of photon number and spin in z direction respectively,(b)and(d)the corresponding average values in Rabi model,respectively

2 绝热制备薛定谔猫态

最近的研究发现:通过利用参量放大的物理方法,不仅可以在压缩表象下实现耦合强度指数倍的增强,还可以实现系统的哈密顿量从最初的弱耦合JC模型转变为强耦合的Rabi模型,即

式中:δ1和δ2为失谐量为Rabi模型的耦合强度。在δ1=0且≥δ2的条件下,考虑(10)式的对称性,原子和电磁模式可以被制备成σˆx表象下的纠缠基态。而对于原来无参量放大的JC模型,根据量子基态的定义式可得即非纠缠基态。利用这种参量放大的方法,如果可以实现缓慢地改变压缩参数r,在系统从JC模型到Rabi模型的转变过程中,由于保持其演化过程的绝热性,系统将会一直停留在其对应的基态,因此就可以实现纠缠基态的绝热制备。考虑单个原子与电磁模式的相互作用的哈密顿量为

式中:χ(t)是二阶非线性驱动项的振幅,而且该振幅是一个含时的缓变参量,ωp则是二阶非线性驱动的驱动频率,为了简化解析过程,假定ω1=ωp。相较于原来的JC模型,在原JC模型的基础上引入了一个额外的二阶非线性相互作用,即(11)式的最后一项。定义自由哈密顿量在这个新的旋转坐标系表象中,引入幺正变换来对角化电磁模式,压缩参数r满足:tanhr= χ/(ω2-ωp)= χ/δ2,且 χ ＜ δ2。在新的压缩表象下可以得到有效的Rabi模型,即

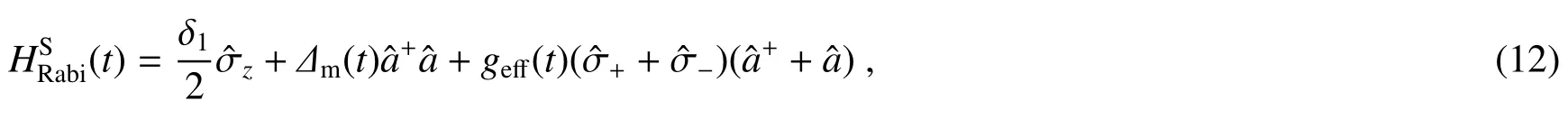
式中:|β〉属于压缩表象下电磁模式的相干态;|±〉x则代表x表象下的激发态和基态,且满足表象变化关系式 |±〉x=(|e〉± |g〉)/。设定相关参数为可通过求解主方程来验证方案的可行性。

另外,在对角化哈密顿量(11)的过程中,实际上得到的总哈密顿量为

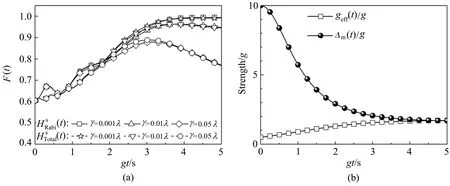
图3 绝热制备薛定谔猫态的动力学演化曲线。在压缩坐标系下,(a)目标态的保真度在总的哈密顿量和有效的Rabi哈密顿量(t)分别作用下的动力学演化对比曲线;(b)有效耦合强度geff(t)和自由哈密顿量的系数Δm(t)随时间的演化规律Fig.3Dynamical evolution curves for adiabatic preparation of Schrdinger cat state.(a)Comparison of dynamical fidelity for the target state governed by the total Hamiltonianand the effective Rabi Hamiltonian(t);(b)Dynamical curves for the effective coupling geff(t)and the free-Hamiltonian coefficient Δm(t)

3 方案的可行性分析

所提出方案具有较为普遍的适用性,如利用光学谐振腔与原子(或人工原子)之间的电偶极相互作用系统、量子超导电路系统、固态电子自旋等都可以实现。由于近年来超导技术的发展日新月异,以超导量子电路作为执行该方案的基本平台[19]。以超导量子比特耦合传输线微波谐振腔为例,可通过电容调节等方法,在微波谐振腔的电磁本征模式中引入二阶非线性驱动,从而实现压缩参量放大[20]。考虑本方案的具体实施并结合当今实验相关进展情况,将本方案所对应的相关实验参数设定为如表1所示。考虑到单个超导比特的相干时间可以达到毫秒量级[19,20],对于绝热的缓慢演化过程,考虑到其演化时间周期为τ≈5/g≈16 ns,故本绝热方案的相干时间足够。

表1 相关参数的设定[19]Table 1 List of the relevant parameters in this scheme[19]

4 结论

从旋转波近似、本征能量和动力学演化这三个方面比较研究了量子Rabi模型和JC模型的异同,发现在弱耦合条件下,Rabi模型完全等价于JC模型;随着耦合强度增加,Rabi模型与JC模型之间存在显著的差异。基于JC模型和Rabi模型的量子基态,利用电磁参量放大使原有的JC弱耦合模型转变为指数倍增强的Rabi强耦合模型,在这个转变过程中找到了一条特殊的基态绝热通道。利用该绝热通道实现了高保真度的薛定谔猫态的稳态制备。另外,还可以利用制备成功的薛定谔猫态来进一步产生奇(偶)相干态,如果对该猫态在表象下进行选择性测量,若测量结果为|g〉态(或|e〉态),则会得到相应的稳态的奇(偶)相干态。由于该制备方案是基态制备且满足量子绝热性,该研究在量子态操控和制备、量子纠缠等领域具有一定的研究意义和应用价值。