全空间上一类Kirchhoff型问题正基态解的存在性
2021-04-27吴燕林钱晓涛
吴燕林, 钱晓涛
( 阳光学院 基础教研部,福建 福州 350015 )
并证明了该问题至少存在一个正基态解.该结果补充了文献[1-4]关于正基态解的存在性结果.
0 引言
本文考虑如下Kirchhoff型问题:
(1)
其中:a,b>0;N=2,3;非线性项幂次4

为了得到问题(1)的正解,本文定义如下泛函:

1 预备知识
给出一些记号:H1(RN)和Ls(RN) (2≤s≤2*)均为标准的Sobolev空间,⇀和→分别表示弱收敛和强收敛,Br(x0)表示以x0为中心、r为半径的球.当无特别指出时,默认为收敛是n→∞情况下的.固定p∈(2,2*),则由H1(RN)的嵌入性质可定义如下:
以下首先证明泛函I具有山路几何结构.
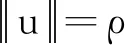
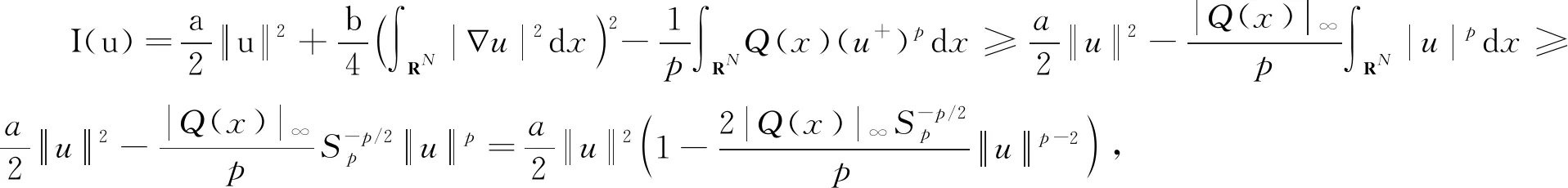
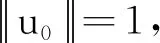
因此存在t0>ρ,使得I(t0u0)<0.令e=t0u0,由此引理1得证.
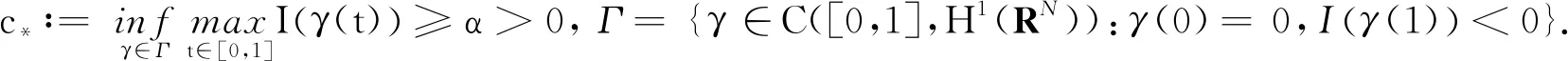
引理2{un}在H1(RN)中有界.
证明由{un}是泛函I的一列(PS)c*序列可知
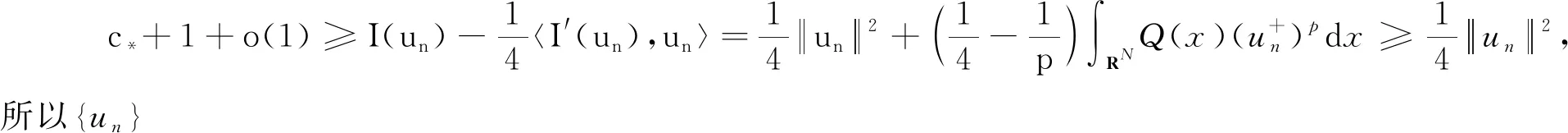
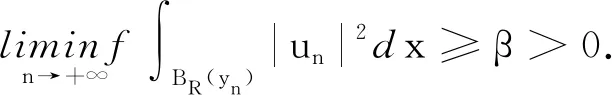
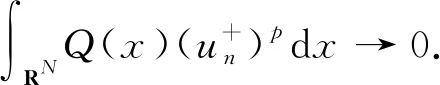
因此un→0于H1(RN).于是有I(un)→0,这与I(un)→c*≥α>0矛盾.引理3证毕.
为了得到方程(1)的基态解,定义如下的Nehari流形:
Λ={u∈H1(RN){0}:G(u)=0},
其中G(u)=〈I′(u),u〉.
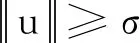
证明对于任意的u∈Λ,有
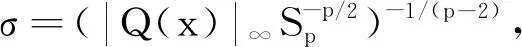
令δ=(p-2)σ2,由此即可证得引理4成立.
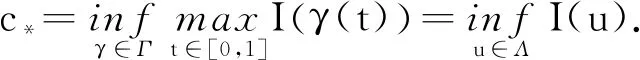
2 主要结果及其证明
定理1问题(1)至少存在一个正基态解.

令vn(x)∶=un(x+yn),则由全空间RN的平移不变性知{vn}也是泛函I的一个有界(PS)c*序列.于是,可以假设v*∈H1(RN)满足vn⇀v*于H1(RN),且vn→v*于L2(BR(0)).又因为
所以v*≠0.

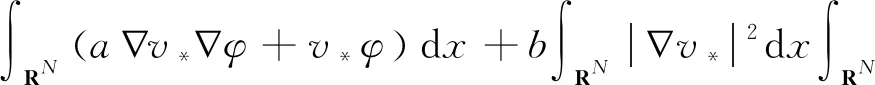
在上式中,取φ=v*,则
(2)
再取t*=t*(v*)∈R+使得t*v*∈Λ,则
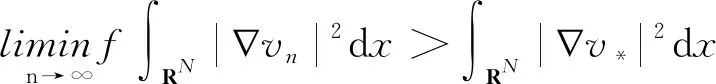
其中第2个不等式使用了Fatou引理,故I(v*)=c*.这表明v*≥0是问题(1)的非平凡基态解.再由标准的正则性提升方法和强极大值原理可知,v*>0.综上可知,v*是问题(1)的正基态解,定理1证毕.
注显然,文献[1-4]的Q(x)均满足本文的条件,因此本文的结果可以看作是文献[1-4]的补充.
