基于巴特沃斯滤波器的傅里叶变换红外光谱处理方法研究

李妍,高闽光,童晶晶,李胜,李相贤,韩昕,刘建国

(1中国科学院合肥物质科学研究院安徽光学精密机械研究所,中国科学院环境光学与技术重点实验室,安徽 合肥 230031;2国家环境保护环境光学监测技术重点实验室,安徽 合肥 230031)

0 引言

傅里叶变换红外光谱法因其实时、连续、在线测量及样品无损检测等特点而普遍应用于工业、环保、医药等领域[1-3]。而基于此方法的傅里叶变换红外光谱仪也受到了广泛关注,随着光谱仪器在各领域的深入普及,对其性能指标的需求也逐渐提升。评价傅里叶变换光谱仪性能指标的主要参数之一是信噪比,而获得高信噪比仪器的主要工作是降低仪器中的干扰噪声。

在傅里叶变换光谱仪中有各种各样的噪声源,如红外光源强度的微小变化、杂散光、外界震动、光谱仪电子学系统中数据采集系统、运放、数据传输接口、干涉仪的动镜抖动及光学元件(如分束器/补偿器)、光学窗口、探测器等[4-6]引起的噪声会降低光谱仪的仪器信噪比。如果仪器本身没有加滤波器滤除这些噪声,那么测量得到的红外光谱图中除了样品产生的吸收峰外,还会包含各种因素引起的干扰噪声,当这些噪声较大或者样品吸收峰很弱时,会造成二者混淆,难以将其区分,以致后续信号处理过程变得繁杂,最终影响样品的定性及定量分析。Yu等[7]研究了基于低噪声运放IV转换和多电平巴特沃斯有源滤波器的前置放大电路,其主要用于获得高光谱探测的有效信号,并未对基于时间分辨的傅里叶变换光谱仪的噪声去除进行阐述。Zhang等[8]使用傅里叶变换红外光谱仪测量窄带滤波器的带外透过率,采用了带阻滤波器来消除主频带内传输的功率,以此获得待研究区域的光谱。而本文研究的傅里叶变换红外光谱仪主要用于中红外样品的测量,因此需要滤除高频以及低频干扰噪声,以免影响待测样品峰形。

鉴于此,本文基于负反馈原理,提出了一种基于巴特沃斯带通滤波器的傅里叶变换红外光谱处理方法,适用于时间分辨的傅里叶变换红外光谱仪。所提出方法主要采用二阶高通滤波器和二阶低通滤波器相结合的巴特沃斯带通滤波器设计,其可以限制经运算放大器预处理的信号带宽,并抑制带外干扰噪声,有效提高仪器信噪比。

1 滤波器参数设计

红外干涉图是包含多种频率成分的带宽信号,信号带宽与红外光源带宽、干涉仪动镜扫描速度、光学元件和探测器的光谱响应带宽及外界干扰噪声频率等因素有关。在进行干涉图的数据采集之前,需要根据实际的测量光谱范围限定干涉图的带宽,因此应设计相应带宽的带通滤波器进行信号滤波,达到限制信号带宽、提高信噪比、抑制带外干扰信号的目的[9]。

首先根据测量光谱范围计算干涉图的频率范围。傅里叶变换红外光谱仪采用波长为632.8 nm的Ne-Ne激光信号,通过干涉仪动镜驱动控制,控制激光调制频率为5 kHz,则调制频率可以表示为

式中:V为干涉仪动镜移动速度,为调制激光的波数。根据(1)式可知,干涉仪动镜的运动速度V=0.158 cm/s。因此双边采样干涉图的光程差速度为Vopd=0.316 cm/s。选择光谱测量波段范围为400～7000 cm-1,计算可得频率范围为126.4 Hz～2.2 kHz,因此带通滤波器的通带宽度fmin～fmax为126.4 Hz～2.2 kHz。

带通滤波器的中心频率容易受到电子部件性能参数的影响,一旦出现频率偏移,滤波器的性能将变差,因此本文选择低通与高通滤波器电路结合的方式[10-12]。对于N阶有源滤波电路的设计,可知其传递函数为

式中:n为UO(S)的阶,m为Ui(S)的阶。根据测量频率带宽,高通滤波器的通带频率设为126.4 Hz,低通滤波器的通带频率设为2.2 kHz,选用低噪声且负载能力强的OP37运算放大器和R、C元件实现巴特沃斯有源带通滤波器[13-15],本研究在如图1所示的常规巴特沃斯滤波器基础上增加了负反馈电路,如图2所示,并对两种滤波电路进行了分析比较。

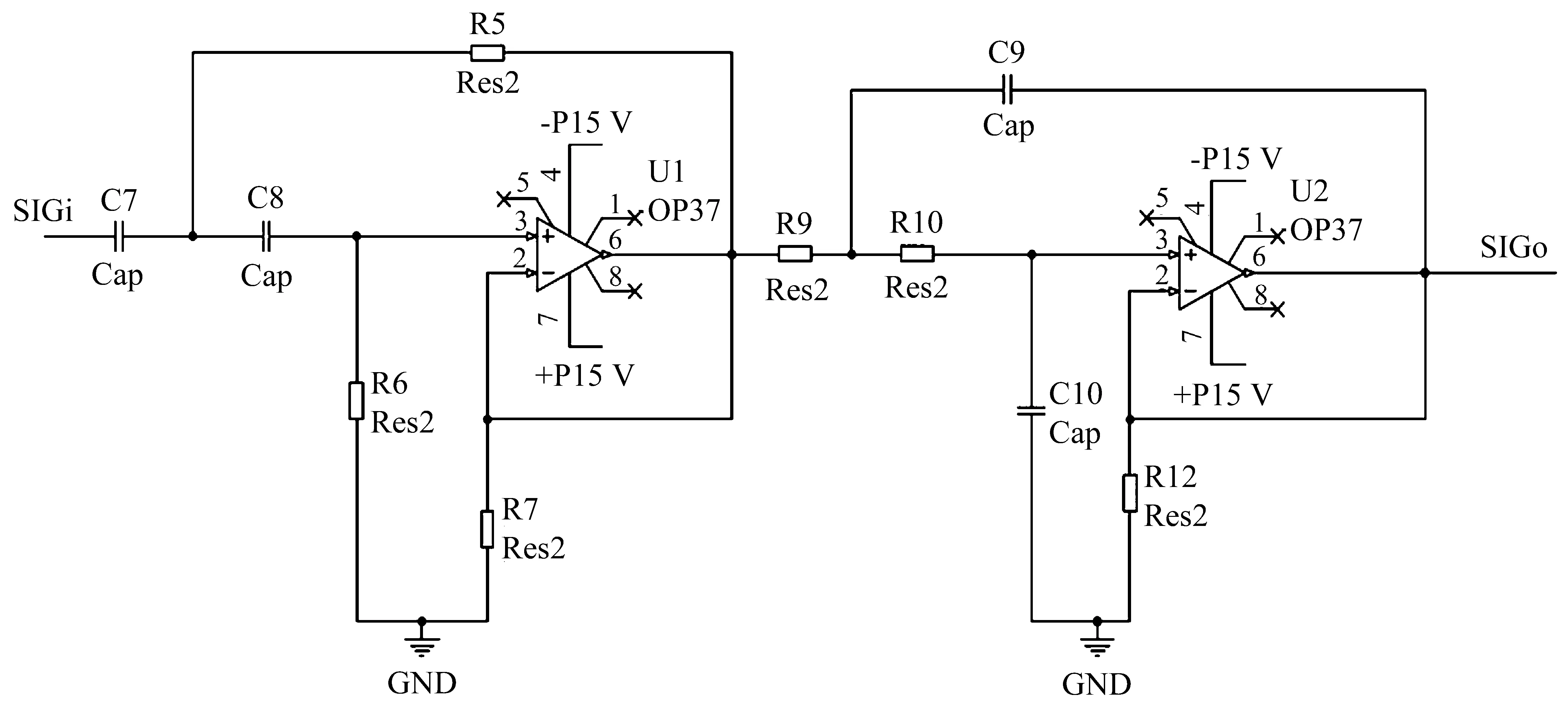
图1 巴特沃斯带通滤波器电路原理图Fig.1 Circuit diagram of Butterworth band-pass analog filter

图2 基于负反馈型巴特沃斯带通滤波器的电路原理图Fig.2 Circuit diagram of the negative feedback Butterworth band-pass analog filter

根据巴特沃斯滤波器电路阶数与增益关系表,可以找到二阶巴特沃斯滤波器增益A=1.586,因此,两级串联的带通滤波器的通带电压增益为A2≈2.515。

考虑元器件参数值误差对传递函数的影响,规定电阻值的容差为1%,电容值的容差为5%。由于每一级电路包含若干电阻和两个电容,且实际元器件参数值与理论计算值相比会有所偏差,因此实际截止频率存在的误差较大;巴特沃斯滤波器在通带具有最平幅度特性,但是从通带到阻带衰减减慢。因而综合考虑滤波器通带宽度与通带衰减的因素,为确保在通带截止频率处的衰减不大于3 dB,以实际截止频率的40%误差75.84 Hz～3.08 kHz来设计电路[16,17]。

选择低通电路的电容值为1000 pF,高通电路的电容值为0.1 μF,电阻值可表示为

式中f为截止频率,为了减小分立元件的分散性,得到低通电阻R9=R10=51.6kΩ,高通电阻R5=R6=21 kΩ。

为了减少偏置电流的影响,应尽可能使加到运放同相端对地的直流电阻与加到反相端对地直流电阻基本相等。因此选择R7=85 kΩ,R12=81 kΩ,由巴特沃斯带通滤波器的幅频特性曲线可知,当品质因子Q=1/(3-AVF)=0.707时[18],其幅频特性曲线最为平坦,计算得到AVF=1.586,因此计算得到R8=(AVF-1)R7=49.8 kΩ,R11(AVF-1)R12=47 kΩ,电阻容差为 1%。

滤波电路第一级为高通滤波电路,其增益A=1.586,根据节点电压法可知,电压传递函数为[19]

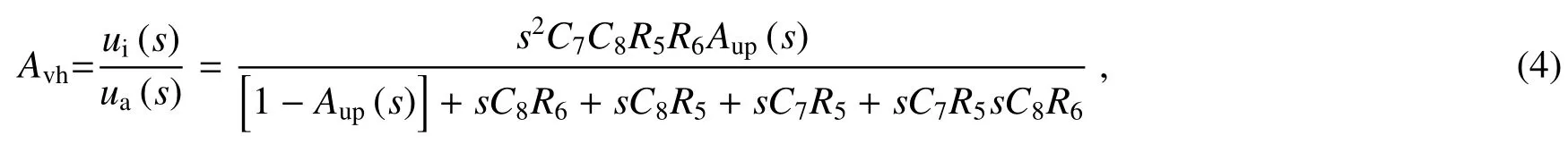
式中Aup(s)=1+R8/R7,令C7=C8=Ch,R5=R6=Rh,则(4)式可简写为

第二级低通滤波电路的传递函数为

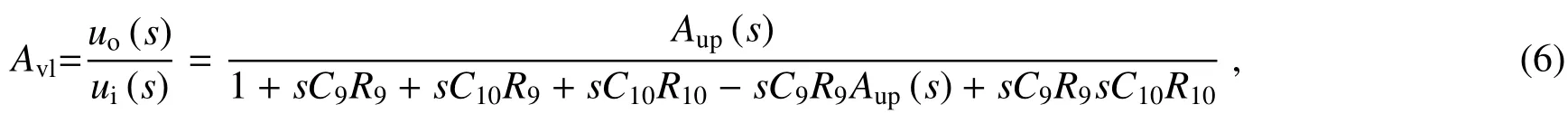
式中Aup(s)=1+R11/R12,为了减小分立元件的分散性[20],令C9=C10=Cl,R9=R10=Rl,则(6)式可简写为

只有当Aup＜3,即分母中s的一次项系数大于0时,电路才能稳定工作,而不产生自激振荡。可知,级联带通滤波电路的传递函数为

2 仿真分析

根据理论计算得到的频率范围75.84 Hz～3.08 kHz,高通滤波电容C7=C8=0.1 μF,高通滤波电阻R5=R6=21 kΩ,反馈电阻R8=(AVF-1)R7=49.8 kΩ,低通滤波电容C9=C10=1000 pF,低通滤波电阻R9=R10=51.6 kΩ,反馈电阻R11=(AVF-1)R12=47 kΩ,R7=85 kΩ,R12=81 kΩ,在电路仿真软件Multisim 10中进行仿真,输入信号为幅值为5 V、频率为3 kHz的正弦信号,得到如图3所示的负反馈型巴特沃斯带通滤波器的幅频及相频特性曲线。

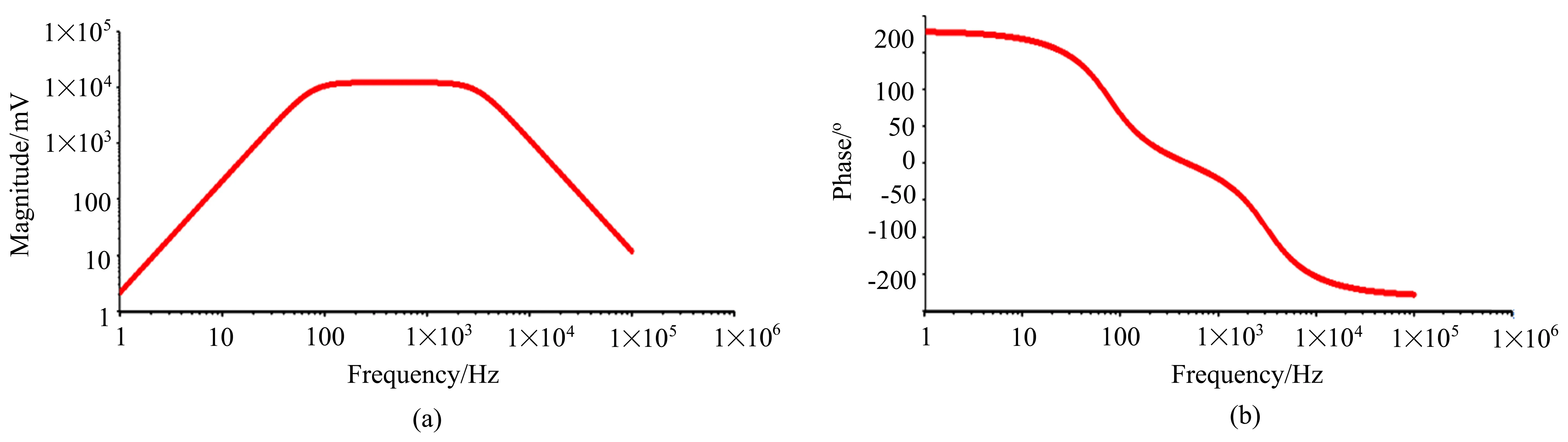
图3 负反馈型巴特沃斯带通滤波器的波特图。(a)幅频曲线;(b)相频曲线Fig.3 Bode plot of the negative feedback Butterworth band-pass filter.(a)Magnitude-frequency curve;(b)Phase-frequency curve

由图3的仿真结果可知,负反馈型带通滤波器中通带最大为12.52,低通截止频率2.2 kHz对应的电压放大倍数为11.13,通带衰减为2.86 dB;高通截止频率126.4 Hz对应的电压放大倍数为11.79,通带衰减为-2.73 dB。因此最大通带衰减为2.86 dB,满足设计要求。

为了进一步说明反馈型带通滤波器的性能指标,在同等参数设置下对无反馈型带通滤波器进行了仿真,结果如图4所示。无反馈型带通滤波器中通带最大为4.76,低通截止频率2.2 kHz对应的电压放大倍数为3.31,通带衰减为3.23 dB;高通截止频率126.4 Hz对应的电压放大倍数为3.67,通带衰减为0.75 dB。因此最大通带衰减为3.23 dB。

图4 无反馈型巴特沃斯带通滤波器的波特图。(a)幅频曲线;(b)相频曲线Fig.4 Bode plot of the Butterworth band-pass filter.(a)Magnitude-frequency curve;(b)Phase-frequency curve

从图3和图4的比较中可以看出,负反馈型带通滤波器与无反馈型带通滤波器相比有更好的截止特性和频率特性,通带内的频率响应更平坦,且有更陡的衰减特性。

3 实验验证

实验采用自主研发的抽取式FTIR光谱仪,光谱分辨率为1 cm-1,光谱范围选择400～7000 cm-1,光谱平均次数设置为32次,切趾函数选择布莱克曼窗函数,光程长(使用长光程多次反射池)约64 m,探测器为斯特林制冷探测器。实验装置原理图及实物图如图5和图6所示。对添加滤波器前后测量得到的光谱数据进行分析处理,得到如图7所示的光谱对比图。图7为增加基于负反馈的巴特沃斯带通滤波器前后测量得到的复原光谱。从图中可以看出,与未加滤波器的测量光谱相比,添加基于负反馈的巴特沃斯带通滤波器的光谱强度增加了大约一倍,更有利于微弱信号的测量。

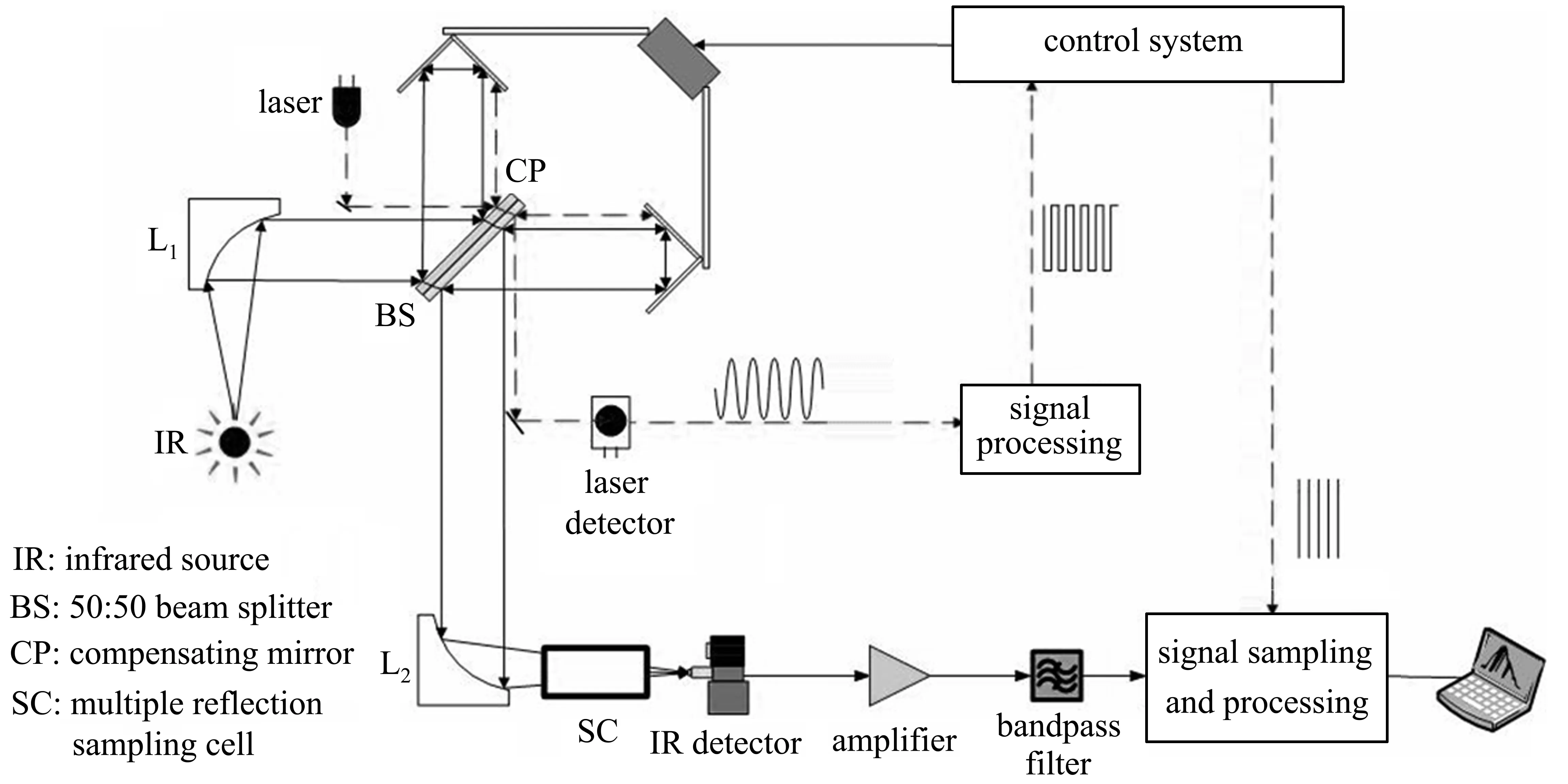
图5 傅里叶变换红外光谱仪装置原理图Fig.5 Schematic diagram of the Fourier transform infrared spectrometer device

图6 实验现场实物图Fig.6 Physical diagram of the experimental site

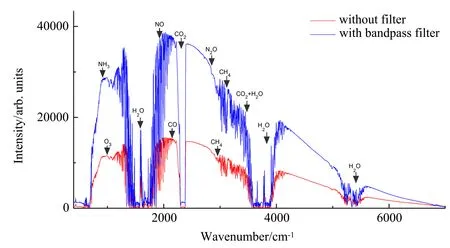
图7 滤波器前后光谱对比图Fig.7 The recovery spectrum with and without a Butterworth band-pass filter

仪器信噪比RSNR通常用来表示红外仪器性能的好坏,可表示为

式中:100是透射率光谱的信号,N是透射率光谱的峰-峰值噪声。

测量仪器的噪声通常选用不受水汽和二氧化碳影响的2100～2200 cm-1和2500～2600 cm-1波段区间。图8所示为2100～2200 cm-1和2500～2600 cm-1波段空气透射率的100%线。根据测量得到的光谱图,结合(9)式计算仪器信噪比,结果如表1所示。在2100～2200 cm-1波段增加滤波器后计算得到的信噪比是未加滤波器得到信噪比的1.83倍,在2500～2600 cm-1波段增加滤波器后计算得到信噪比是未加滤波器得到信噪比的1.96倍。由此可知在干涉图后增加带通滤波器可以有效地提高仪器信噪比。

表1 增加带通滤波器前后复原光谱信噪比Table 1 Comparison of SNR for output spectrum with and without a Butterworth band-pass filter

图8 空气透射率的100%线.(a)2100～2200 cm-1;(b)2500～2600 cm-1Fig.8 The transmittance spectrum.(a)2100～2200 cm-1;(b)2500～2600 cm-1

4 结论

研究了基于巴特沃斯带通滤波器的傅里叶变换红外光谱数据处理方法,对带通滤波电路的传递函数进行了理论推导,结合光谱仪相关指标得出了滤波器电路参数与元件值的对应关系,然后利用软件仿真确定了电路元件参数的范围,并进一步通过实验进行优化直至满足设计要求指标,最终将其用于光谱仪中,对比分析了增加滤波器前后测量得到的仪器信噪比。实验结果表明:基于巴特沃斯滤波器的红外光谱处理方法在2100～2200 cm-1和2500～2600 cm-1波段得到的仪器信噪比分别为未加滤波器的传统处理方法得到的仪器信噪比的1.83倍和1.96倍。由此表明:基于巴特沃斯带通滤波器的数据处理方法可以降低带外干扰噪声,提高仪器信噪比,进一步改善仪器的性能指标。