车用复合材料层合板在弯曲载荷下损伤行为分析

孟翔耀，董万鹏

（201600 上海市 上海工程技术大学）

0 引言

1970 年后纤维增强金属复合材料出现，因其不光具有金属材料良好的导电传热性能，而且具备纤维复合材料比模量大、耐腐蚀等优点，被大规模运用于航天航空工业、船舶制造、高端汽车制造等领域。

在对复合材料的研究中，堵同亮[12]建立了编织复合材料成形的数值模型，并研究了铺层角度对成型性能的影响；贾利勇[14]基于ABAQUS软件，采用多次计算的刚度衰减方式，设计了基于应变的Chang-Chang失效准则VUMAT子程序，预测了冲击损伤后的复合材料抗拉强度。

复合材料因其各向异性材料纤维与基体分布的随机性，在力学性能分析和材料损伤失效预测方面受到很大的限制，也缺乏对复合材料宏观形变过程中材料损伤演化与断裂失效的认识。本文通过ABAQUS 采用Hashin 失效准则与内聚力损伤模型结合的方式提出一种预测复合材料宏观力学性能与损伤失效的模型，并通过该模型分析铺层方向对纤维增强铝合金层合板力学性能的影响。

1 材料模型

1.1 层合板失效模型

Hashin 准则作为复合材料损伤准则被广泛运用在预测纤维和基体的拉伸、压缩损伤，考虑到三维应力状态的Hashin 准则形式为纤维拉伸/压缩失效[1]，具体表达如下：

纤维拉伸失效（σ11>0）

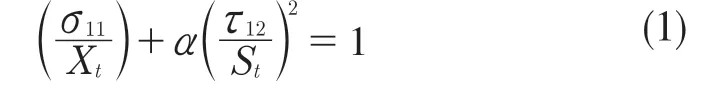
纤维压缩失效（σ11<0）

基体拉伸失效（σ22≥0）

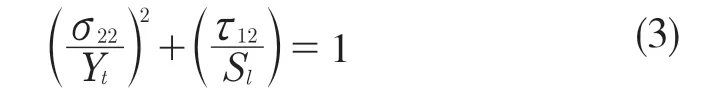
基体压缩失效（σ22≤0）

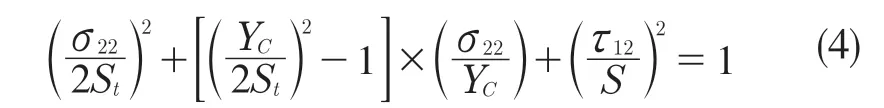
式中：Xt——单层板的纵向拉伸强度；Xc——单层板的纵向压缩强度；Yt——单层板的横向拉伸强度；Yc——单层板的横向压缩强度；Sl——单层板的纵向剪切强度；St——单层板的横向剪切强度；α——剪切修正系数[1]。

1.2 内聚力损伤模型

近年来，国内外对材料在不同条件下发生分层失效进行研究，提出并改进多种内聚力模型，根据牵引力分离准则曲线形状做出划分。其中，最主要的内聚力模型有双线性内聚力模型、指数型内聚力模型和梯形内聚力模型[2]。在研究复合材料分层失效时，双线性内聚力模型应用因其简单实用得到广泛的关注，因此本文选择基于最大名义应力损伤初始准则的双线性内聚力模型，应用到研究层合板冲击损伤当中。双线性本构响应如图1 所示[3]。

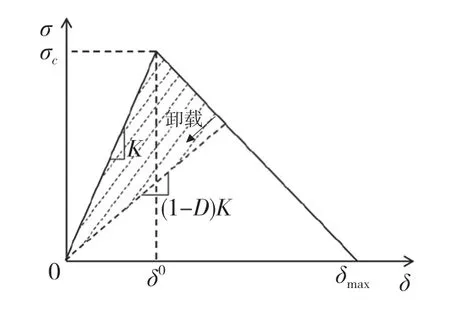
图1 双线性 traction-separation 本构响应Fig.1 Bilinear traction-separation constitutive response

在复合材料层合板未发生分层损伤时，层间单元为线弹性本构模型，如式5 所示。

式中：σn——界面正应力；τs，τt——剪切应力；Kn，Ks，Kt——相应的界面刚度；δn，δS，δt——与刚度对应的位移，3 个方向的位移分别为3 种裂纹扩展模式[4]。

当层间到达损伤起始后，随着载荷的增加，内聚力单元产生损伤，单元产生刚度退化开始进入损伤演化状态[5]。内聚力模型的损伤演化分析方法有2 种：基于等效位移或者基于断裂能[5]。本文选择基于断裂能的 B-K 失效准则。B-K 准则能很好地模拟单层板之间的分层破坏演化情况。内聚力单元刚度退化方程如式（6）：

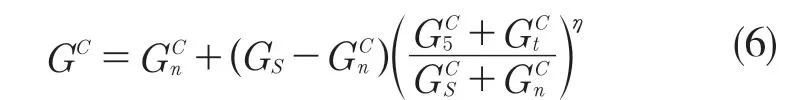
式中：Gc——混合型分层演化的界面断裂能释放率；，，——界面在法向和两个剪切方向失效所需要的断裂能量；η——界面性能参数，研究表明纤维增强复合材料取值为 1-2 较为适合[6]。

2 模拟分析

本文用AL6061 作为面板材料，碳纤维T700作为夹芯材料，根据CF/AL 宏观结构特征建立三维模型，如图2 所示。其中w=150 mm，l=15 mm，单层铝板厚度0.3 mm，单层碳纤维厚度为0.3 mm。

图2 层合板弯曲模拟图Fig.2 Simulation of laminate bending

在ABAQUS 内建立碳纤维增强铝合金层合板三点弯曲模型，模型尺寸参考实际实验尺寸，铺层顺序为[0/90]层合板两面粘结铝合金薄板，如图2 所示。为节约计算成本，采用X-X，Y-Y对称建模。采用显示动力分析步进行分析，分析时间为0.5 s。碳纤维单层板采用SC8R 单元，铝合金薄板采用C3D8R，最小单元尺寸为0.5 mm×0.5 mm×0.3 mm。

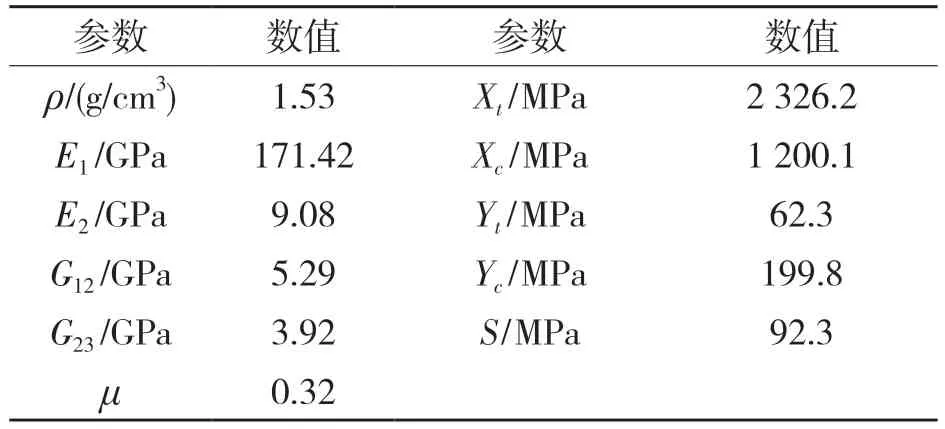
表1 层合板材料参数Tab.1 Material parameters of carbon fiber/epoxy resin

在单层板与单层板、金属薄板与单层板之间插入Cohesive 单元，模拟层间失效，Cohesive 单元的厚度为0.01 mm。表2 为界面性能参数，表3 为6063 铝合金材料参数。材料之间摩擦系数为0.3，法向行为硬接触。

表2 界面层力学性能Tab.2 Mechanical properties of interface layer

表3 6063 铝合金材料参数Tab.3 Material parameters of Al6063

3 结果分析讨论

3.1 [0/90]模拟结果分析

图3—图7 为AI/C 层合板[0，90]在压头的作用下逐渐发生纤维与基体失效各层的损伤失效程度。随着位移载荷逐渐增大，层合板出现变形，应力主要集中在压头与层合板接触处、材料支撑处，最大应力位于0°层中心部位达到1.792×108Pa。

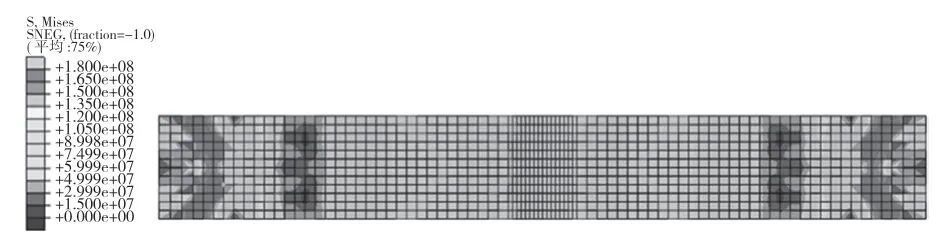
图3 0°层应力分布云图Fig.3 Nephogram of stress distribution in 0°l ayer

图4 0°层损伤云图Fig.4 Nephogram of damage in 0°l ayer

图5 90°层应力分布云图Fig.5 Nephogram of stress distribution in 90°l ayer

图6 90°层损伤云图Fig.6 Nephogram of damage in 90°l ayer

图7 90°层间的损伤起始云图Fig.7 Initial nephogram of damage between 90° layers

在0°层，应力主要集中于材料支撑位置，中心与支撑位置间为应力最小部分。纤维拉伸失效主要发生在材料中间部分，越靠近中心损伤的比例越高，随着载荷的增加向两边扩展。纤维压缩损伤主要发生在材料支撑处，基体的损伤主要分布于支撑与中心处且向两边逐渐扩展。

在90°层，单层板的应力主要集中于中心与支撑处，最大应力出现在中心两侧为1.113 28×108小于0°层的最大应力。材料纤维损伤很小，90°层主要发生基体损伤，基体拉伸损伤主要集中在单层板中部，基体压缩损伤主要发生在支撑处。

图8 为3 个单层板的层间损伤起始云图。基于最大应力准则作为层间失效判据，图8（a）为铝板与0°层间的损伤起始云图。从图中可以发现，材料中心为层间损伤层间失效最小处，3 个界面分层趋势状态略有不同，铝板与0°层间的损伤起始值出现在支撑处，而0°层和90°间界面峰值出现在材料两侧。

对比两个0°与90°层可以发现，0°层多出现纤维的拉伸损伤。如图4（a）所示，0°层主要承受横向的拉升载荷；如图6（d）所示，90°层多出现基体的压缩载荷，且并未出现纤维的压缩损伤纤维拉升损伤也较小。可见90°主要承受纵向的压缩载荷。

3.2 不同铺层角度层合板力学性能对比

对比两种不同铺层顺序下金属复合材料层合板在相同载荷、边界条件下的模拟结果，研究铺层顺序对力学性能与破环情况的影响。图8 为[0/90]，[90/0]两种铺层顺序下的载荷-位移曲线。从图上可以发现两种层合板随着位移的增载荷逐渐增加，达到最高值后曲线趋于平缓。

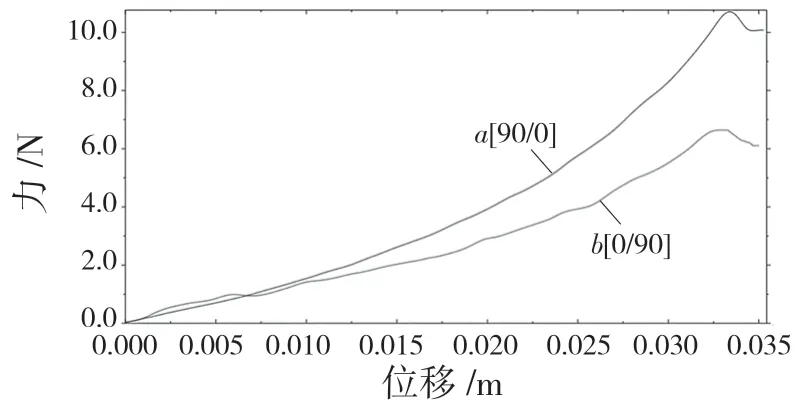
图8 铺层方向对层合板性能的影响Fig.8 Influence of lay-up direction on laminate performance

层合板中，0°方向为纤维铺层方向，90°方向为垂直于纤维铺层方向。0°时，单层板拉伸强度为2 326.2 MPa，压缩强度为1 200.1 MPa；90°层的拉伸强度为62.3 MPa，压缩强度为199.8 MPa。0°层强度远大于90°层强度。在层合板承受三点弯曲时，主要由0°方向的纤维承受载荷。在相同弯曲载荷的情况下，外部层的应变大于内部层应变。[0/90]这种铺层方式，0°层为外部铺层，相同载荷条件下应变大将会先破坏；[90/0]这种铺层方式，0°层为内部铺层，应变小将可以承受更大的弯曲载荷。通过以上分析可以发现[90/0]层合板有更高的弯曲性能。

从纤维的压缩损伤云图可以发现，当载荷达到最高点后，基体出现压缩失效单元被删除，同时[0/90]先于发生纤维压缩失效。[0/90]层合板的载荷峰值为6.7 N，[90/0]层合板的载荷峰值为10.9 N。对以上结果可以发现，[90/0]层合板有更高的弯曲性能。

4 结论

基于Hashin 失效准则与内聚力模型建立有效的力学有限元模型，该模型可以有效预测纤维金属层合板在三点弯曲时的纤维拉伸损伤、纤维压缩损伤、基体拉伸损伤、基体压缩损伤以及层间失效。在以上结果与理论的基础上，通过分析2 种铺层方向的载荷-位移曲线与损伤云图，结果表明铺层方向为[90/0]有更好的弯曲性能。