基于特征筛选和代价敏感学习的财务预警研究

任婷婷 鲁统宇（教授） 张伟楠 （中国计量大学经济与管理学院 浙江杭州 310018）

一、引言

随着全球经济的不断发展，上市公司受到国内外各方面的冲击和压力持续增大，内外部不确定因素的增多使得企业经营的难度日益增大，一旦管理不善就可能导致企业的业绩下滑甚至发生破产。而财务困境一旦发生不仅会给企业带来严重的负面影响，还会造成股市的动荡，伤害投资者的利益。对上市公司进行财务预警，可以帮助企业提高警惕，改善财务状况，避免财务困境的发生；也可以给银行、基金等相关机构释放投资信号，避免遭受损失。因此，构建有效的财务困境预警模型有着重要的现实意义。

二、文献综述

在现有研究中，财务预警常被视为二分类问题来处理，即以上市公司是否被特殊处理（Special Treatment，ST）作为划分标志，研究的重点在于如何构建有效的预测分类模型。近年来，关于财务预警的研究取得了重大进展，采用的方法可大致分为统计学习和机器学习。Fitzpatrick［1］和Beaver［2］利用单变量模型进行财务预警，但该模型强烈依赖于单一指标，结果较不稳定。在单变量模型预测的基础上，Altman［3］运用多元线性判别分析，将22个初始财务比率指标筛选为5个变量，并以此构造了Z-score模型，该模型准确率较高，并在财务预警领域得到了广泛的应用。国内关于预警模型的研究起步相对较晚，周首华等［4］在Z-score模型的基础上添加现金流量因素，构建了F分数模型；杨淑娥和徐伟刚［5］则将主成分分析和Z-score相结合构建了Y分数模型，两个模型均能取得良好的预测结果。随着计算机技术的发展，机器学习方法的兴起为财务预警问题提供了一个新思路，其也因准确率高、泛化性能强等优点得到了广泛的应用。Ohlson［6］以105家困境公司和2 058家健康公司为研究对象，将Logistic回归分析应用于财务预警问题中。Ding et al.［7］和 Gogas et al.［8］分别将支持向量机应用于中国企业和美国企业，均取得了比统计学习方法更好的预测性能。Shahbazi［9］分析并构建了决策树模型，对银行客户的风险预警取得了89.38%的预测准确率，性能优秀。不同的文献针对模型的好坏有各自的见解，统计模型虽然所需参数少、结构简单、训练时间短，但仍然会受到统计假设以及多重共线性等因素的影响［10］，而机器学习最大的问题就是调参过程繁琐和模型的可解释性不足。

现有的一系列研究表明学者对财务预警问题的关注，建立的模型结果具有一定的借鉴意义。然而财务预警领域中普遍存在特征冗余问题，数据之间强烈的相关性不仅会造成模型的训练时间过长，也会对准确率产生负面影响。因此，部分学者进行了针对性的研究：宋鹏等［11］利用粗糙熵的方法筛选特征，并在此基础上利用Logistic回归建立了RS-Logistic预警模型，该模型比传统Logistic模型的准确率高；罗康洋和王国强［12］利用改进MRMR算法进行特征选择，得到了更为简洁、准确的特征集；游俊红［13］构造了现金流量指标体系，利用熵权理论对不同指标赋予权重以进行特征筛选，研究结果证明了模型的可行性和实用性。

此外，在财务预警领域中，发生财务困境的企业要远远少于未发生财务困境的健康企业，此类数据分布不平衡问题会使传统模型在学习过程中发生偏移，导致少数类样本分类准确度不高，而ST公司的正确预警正是该领域研究重点关注的对象，是衡量模型的重要标准。针对此类问题，现有研究主要从数据和算法两个层面进行改进。数据层面是指利用重采样平衡原数据集的类别分布比例以消除不平衡性，可分为欠采样、过采样和混合采样。欠采样和过采样分别通过减少多数类样本和增加少数类样本的方式平衡数据集，混合采样则将两者结合。Chawla et al.［14］提出了一种随机过采样的改进算法——合成少数类过采样技术（SMOTE），该方法在不平衡分类领域应用广泛。夏利宇和何晓群［15］利用迭代逆向重抽样使模型的关注中心由多数类转移至少数类，并将各弱分类器集成为强分类模型，该模型在真实数据集中的表现良好。算法层面则是对原有模型进行改进以更加适应不平衡数据集的特殊分类需求，包括代价敏感和集成学习。代价敏感的基本思想是通过引入代价敏感因子改变分类器的内部构造，使其错分代价最小［16］，而集成学习则将若干个基分类器集成，通过综合多个分类器的分类结果以获得更好的模型性能。其中的著名代表是Fraud和Schapire［17］于1997年提出的AdaBoost算法，其基本思想为：在基分类器训练过程中，不断增大错分样本的权重，而相对减小对分样本的权重，从而提高错分样本在模型中的重要性。AdaBoost算法的分类准确率高，已被广泛应用到财务预警领域中。Tao et al.［18］将代价敏感支持向量机作为基分类器，改进AdaBoost框架的样本权重更新公式，构建了一个以少数样本分类准确率为目标的分类模型。顾玉萍和程龙生［19］以马田系统作为AdaBoost的基分类器，对2010—2015年间的财务危机进行预警研究，证明集成算法模型的分类效果要优于其他的单一分类器。

基于此，本文重点研究财务预警领域中的特征冗余和数据分布不平衡问题。首先通过双重显著性检验和主成分分析进行特征筛选与降维，之后将错分代价引入多个机器学习算法以构建代价敏感模型，实证研究中的对比分析和稳健性检验证明了该模型的有效性和稳健性。

三、机器学习算法及代价敏感学习

（一）机器学习算法

1.逻辑回归（Logistic Regression，LR）。逻辑回归是一种用来处理二分类问题的模型，通过线性回归和Sigmoid阶跃函数得到。首先为每个特征变量xi乘一个回归系数wi，将其相加得到线性回归模型。之后通过Sigmoid阶跃函数得出分类结果，概率大于0.5的被分入1类，小于0.5的被分入0类。线性回归模型和Sigmoid阶跃函数形式如式（1）和式（2）所示 ：

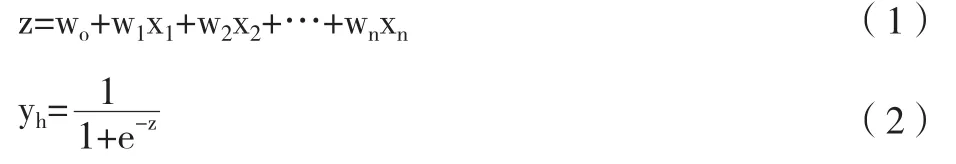
综合两式，可得到LR模型的常用表达公式为：

2.支持向量机（Support Vector Machines，SVM）。传统SVM以总体样本分类准确度最高为模型目标，目的是求解能正确划分数据集的超平面，并使分割超平面的几何间隔最大。其基本思想为：设训练样本集D={（Xi，Yi）}，i=1，2，…，n；Xi∈Rn，n 代表特征向量维数；Yi∈（-1，+1）代表不同的分类类别。若样本集D线性可分，则SVM需要找到一个最优超平面ωTx+b=0将两类样本分开，其中ωT为法向量，b为位移项；当样本集线性不可分时，引入松弛变量ξi≥0和惩罚因子C，C表示对错分类样本的惩罚程度，取值越大代表惩罚力度越大，此时的目标函数为：

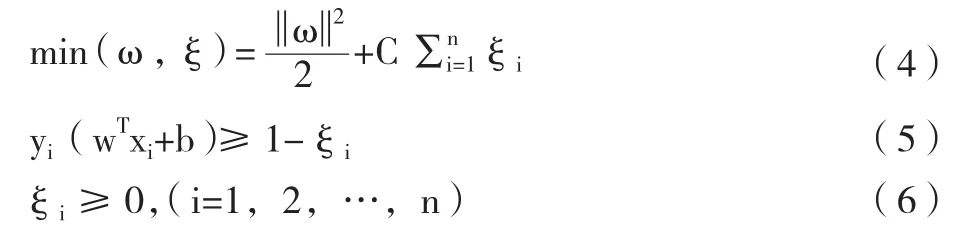
3.决策树（Decision Tree，DT）。决策树是一种自上而下的贪心学习算法。它从根节点开始，根据事先设定的划分属性获取分支节点，并通过遍历得到一个树状的分类模型。分支节点包括内部节点和叶节点，前者代表对某个属性进行测试，后者则对应最终的决策结果。

为避免模型过拟合，需对初始生成的决策树进行剪枝。剪枝以是否带来泛化性能的提升为判断依据，按照操作顺序分为预剪枝和后剪枝。预剪枝在决策树分裂过程中进行，若某个内部节点的分裂没有提升整体的泛化性能，则拒绝划分并将其标记为叶节点。后剪枝则在决策树生成后进行，如果某内部节点替换为叶节点会带来泛化性能的提升，则进行替换。在决策树生成过程中，常用的划分最优属性的标准包括信息增益、信息增益比率和基尼系数，分别构成ID3、C4.5和CART决策树。

（二）代价敏感学习

传统的分类算法基于误分类代价相等的假设，以整体的分类准确率最高为模型目标，忽视了不平衡数据中少数类样本的特殊性，对其几乎没有识别能力，即使总体的分类准确率高，但困境企业的分类准确率很低。而在现实生活中，因ST企业的错误预警会给社会带来更为严重的影响，所以需重点关注模型对少数类样本的识别能力。

利用代价敏感学习处理数据不平衡问题的原理在于：给予少数类以较大的错分代价，多数类以较少的错分代价，并以总体错分代价最低为模型目标，使模型在构建过程中为降低总体的错分代价而重点关注少数类样本，从而有效改善传统模型的学习偏移问题［16］。

1.代价敏感逻辑回归（Cost-sensitive LR，CS_LR）。为适应不平衡样本集的分类需求，克服传统逻辑回归在不平衡二分类问题上的不足，本文通过对数据集中少数类和多数类样本赋予不同的错分代价，得到CS_LR模型。

2.代价敏感支持向量机（Cost-sensitive SVM，CS_SVM）。在CS_SVM中，通过为不同类别设置不同的错分代价，得到代价敏感支持向量机（Cost-sensitive SVM，CS_SVM）模型（Dhar和Cherkassky，2015），此时模型的目标函数为：

其中，n+代表少数类样本数量，n-代表多数类样本数量，C+代表少数类划分为多数类的错分代价，C-代表多数类划分为少数类的错分代价。

3.代价敏感决策树（Cost-sensitive DT，CS_DT）。在决策树生成过程中，不平衡数据集的类分布会影响到分裂节点的选择［21］，导致传统模型在生成和剪枝过程中偏向多数类样本的分类准确率。将错分代价引入决策树，改变了节点的分裂和剪枝标准［22］，并以总体错分代价最小为模型目标，少数类样本较高的错分代价权重使得其在模型训练过程中的重要性增强，得到的CS_DT模型可有效应对财务预警中的不平衡二分类问题。

四、基于特征选择与代价敏感的财务预警模型研究设计

（一）样本与指标筛选

1.样本选取。本文选取沪深A股制造业的企业为研究对象。此外，证监会的相关文件显示，企业在t年被ST的一个主要原因是其在前两年内持续亏损，因此t-1年和t-2年的财务数据对困境预警分析的意义不大［23］。同时为了保证模型的谨慎性，本文以t-3年的财务数据为基础进行研究分析。数据来源于Wind数据库，操作均用Python 3.6实现。

样本的选取参考田宝新和王建琼［24］的步骤：首先从Wind数据库中提取沪深A股上市公司中在2019年内因“财务状况异常”而被ST或*ST的制造业类别企业，在剔除上市时间不足3年以及数据缺失过多的企业后，得到52个ST样本；其次，根据行业和资产规模相匹配的原则，按照1∶3的比例选择156家非ST企业；最后，将这208个样本与其2016年的年度财务数据相匹配得到最终数据集。之后，对获得的数据集进行预处理：对离群值进行1%双侧缩尾处理；用各指标的中值填充缺失值；对数据进行最大最小标准化处理。

参考相关文献，本文依据科学性、严谨性和完整性的原则选取了43个财务指标，这些指标涵盖了企业的偿债能力、盈利能力、营运能力、成长能力、股东盈利能力和现金流量能力等。同时，选取了7个非财务指标作为补充，最终得到的指标体系如表1所示。

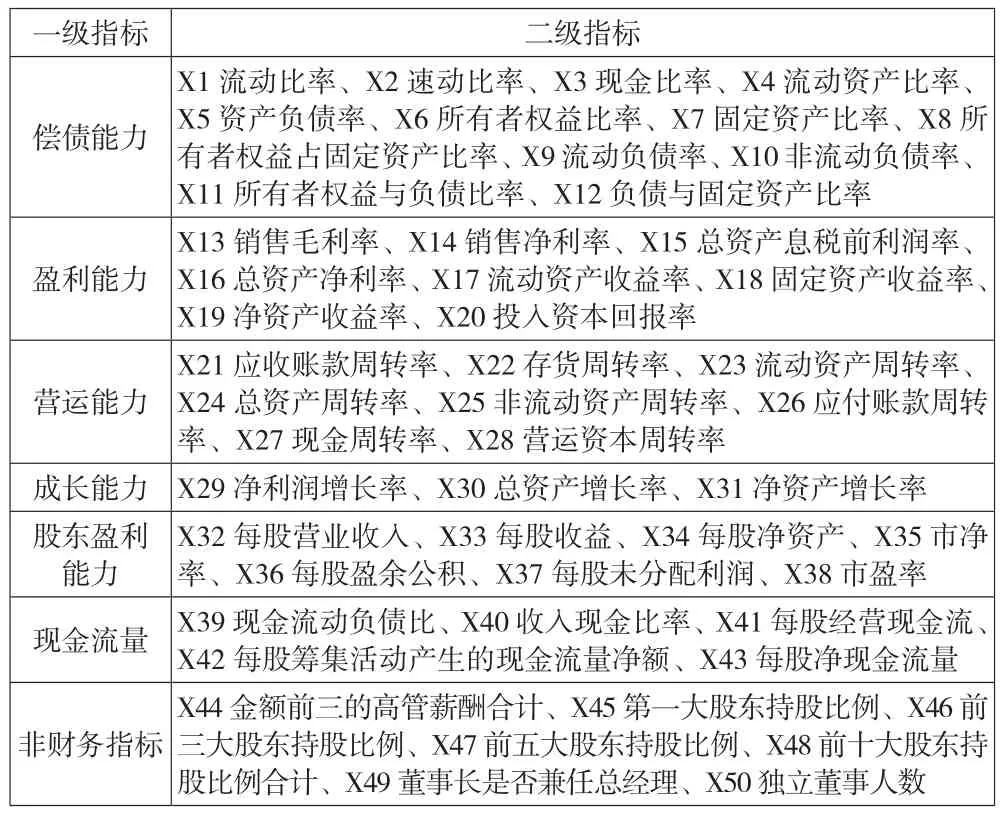
表1 财务预警模型指标体系

2.双重显著性检验。本文把发生财务困境的ST企业记为“1”，未发生财务困境的健康企业记为“0”，分为两组样本，之后通过双样本Kolmogorov-Smirnov（K-S）检验和Mann Whitney-U（MW-U）检验对初始指标体系进行显著性检验，逐一判断各个指标的取值在两个组别之间是否存在显著差异。K-S检验和MW-U检验均为非参数检验，不要求数据服从特定分布，前者用来检验两总体分布是否存在显著差异，后者用来检验两个总体的中位数是否一致。根据检验结果：X8、X9、X21、X22、X25、X26、X27、X28、X29、X32、X40、X42、X43、X44、X49 和 X50 等16个指标在两个检验的P值均大于0.05，说明这些指标无法对两类企业进行区分，故将其删去，保留剩余34个指标。

3.主成分降维。主成分分析（Principal Components Analysis，PCA）是财务预警研究中常用的特征降维方法［23，25，26］。其基本思想是利用正交变换将原始变量投影为一组相互独立的主成分，并确保这些主成分能够涵盖原始数据集的所有信息，从而消除冗余变量，避免数据之间的相关性对模型准确率产生影响。本文在双重显著性检验的基础上进行主成分降维，最终得到的8个主成分涵盖了原34个指标80%以上的信息，结果如表2所示。

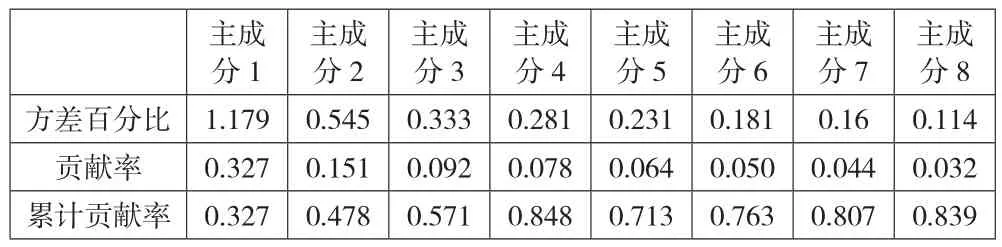
表2 主成分分析结果

（二）参数设置

代价敏感学习中的错分代价通常由代价矩阵得出［21］，但一个企业被错误预测带来的经济损失往往需要经过长时间的实践或者采取专家学者的建议，真实的错分代价很难界定和获取。为保证模型的简便性，本文认为错分代价和数据集的不平衡程度有较大关系［12］，引入的少数类和多数类的错分代价分别如下所示：

其中，n+和n-分别表示少数类和多数类样本数量，n为样本总量。

（三）模型评价指标

传统分类模型一般以样本总体的分类准确率（Accuracy，ACC）作为评价指标，而在不平衡分类中，模型受多数类样本的影响较大，即使少数类样本全部被错分为多数类样本，也能取得较高的准确率，无法评价模型的真实性能。因此，本文引入少数样本分类准确率（True Positive Rate，TPR）以衡量模型预测ST企业的能力，多数样本分类准确率（True Negative Rate，TNR）以衡量模型预测非ST企业的能力。

此外，本文使用综合指标AUC和G-mean值来评价分类器的整体分类性能。AUC是衡量分类器优劣的一个通用性能指标，其被定义为ROC曲线下的面积，得分不会受到数据集样本分布的影响，且值越大表示分类器效果越好；G-mean则是TPR和TNR的综合指标，反映分类器的总体分类性能，只有TPR和TNR得分均高时，G-mean得分才会较高。TPR、TNR和G-mean值可通过混淆矩阵（表3）求得，计算公式分别如式（12）-（14）所示。

表3 混淆矩阵

五、实证分析

（一）模型结果分析

在实验过程中，本文按照7∶3的比例将初始数据集划分为训练集和测试集，前者用来获取最优参数，后者则用来检验模型性能。同时，为避免随机性对模型准确率造成干扰，本文进行了50次重复实验，并将传统机器学习模型定义为Model_Basic，代价敏感模型记为Model_CS，每个模型的得分均为三种机器学习方法的均值。Model_Basic和Model_CS在50次重复实验中各个指标上的得分情况如图1所示。可知，Model_CS比Model_Basic在G-mean值、AUC值和TPR值上均有提升，其中TPR值即ST企业的分类准确率有明显提高，从而证明了代价敏感模型在不平衡财务预警方面的优势。与此同时，TNR值在加入代价敏感因子之后有所下降，出现上述现象的原因在于二分类问题中由于受到样本随机和容量有限等问题的影响，很难实现TPR和TNR的同时提升［27］。在此基础上，将Model_CS和Model_Basic进一步分解，得到的基础模型在各个指标上的最终得分如下页表4所示。

由下页表4可以看出，三个传统的机器学习模型在考虑错分代价后得到的代价敏感模型在ST公司的分类准确率上有显著的提升，这对财务预警领域来说尤为重要，证明了代价敏感学习方法的适用性和优越性。

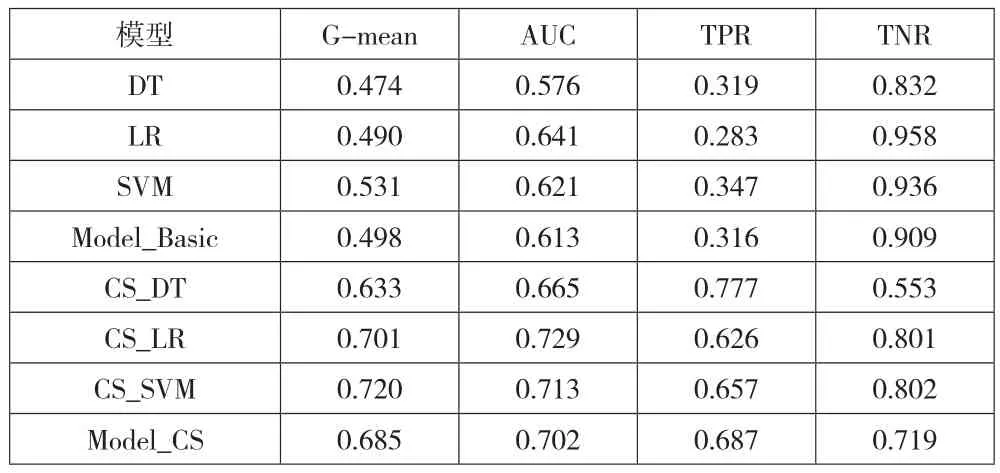
表4 基于代价敏感的财务预警模型实验结果

另外，在三个代价敏感模型中，CS_DT模型的表现值得关注。虽然该模型在TPR上的得分最高，但其大幅提升是以牺牲TNR值为代价的，TNR值得分从0.832降至0.553，导致AUC值和G-mean得分较低。虽然财务预警领域重点关注TPR值的提升，但TNR值过小同样无法接受，故认为将CS-DT模型用作财务预警的风险较大。而CS_SVM和CS_DT在各指标上得分均良好，证明了其在不平衡财务预警领域上的适用性和可靠性，而前者在G-mean，TPR和TNR上得分更高，性能更优。

（二）稳健性检验

为探讨代价敏感模型在不同不平衡率下的表现，本文又采用1∶5的不平衡比率对上述模型进行稳健性检验，得到的最终结果如表5所示。

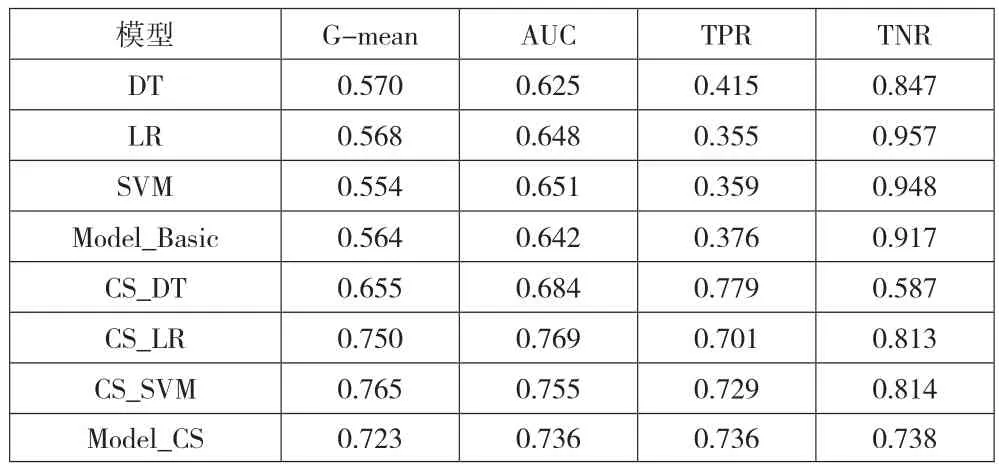
表5 各模型稳健性检验结果

由表5可以看出，当不平衡程度增大至1∶5时，初始模型在TPR上的平均得分不到0.4，说明只有不到40%的ST样本被正确检测出来，这在财务预警领域是不可接受的，而代价敏感模型的TPR平均得分达到了0.736，进一步印证了代价敏感模型可以有效处理上市公司财务预警中的样本分布不平衡问题。此时的CS_DT模型仍不稳定，TPR上得分高达0.779，而TNR得分最低，为0.587，导致在AUC值和G-mean值上得分最低，总体表现最差，而CS_SVM模型仍然表现最好。因此，在不同的不平衡率下，本文具有一致的研究结论。在稳健性检验中，Model_Basic和Model_CS在50次重复实验中的得分情况如图2所示。

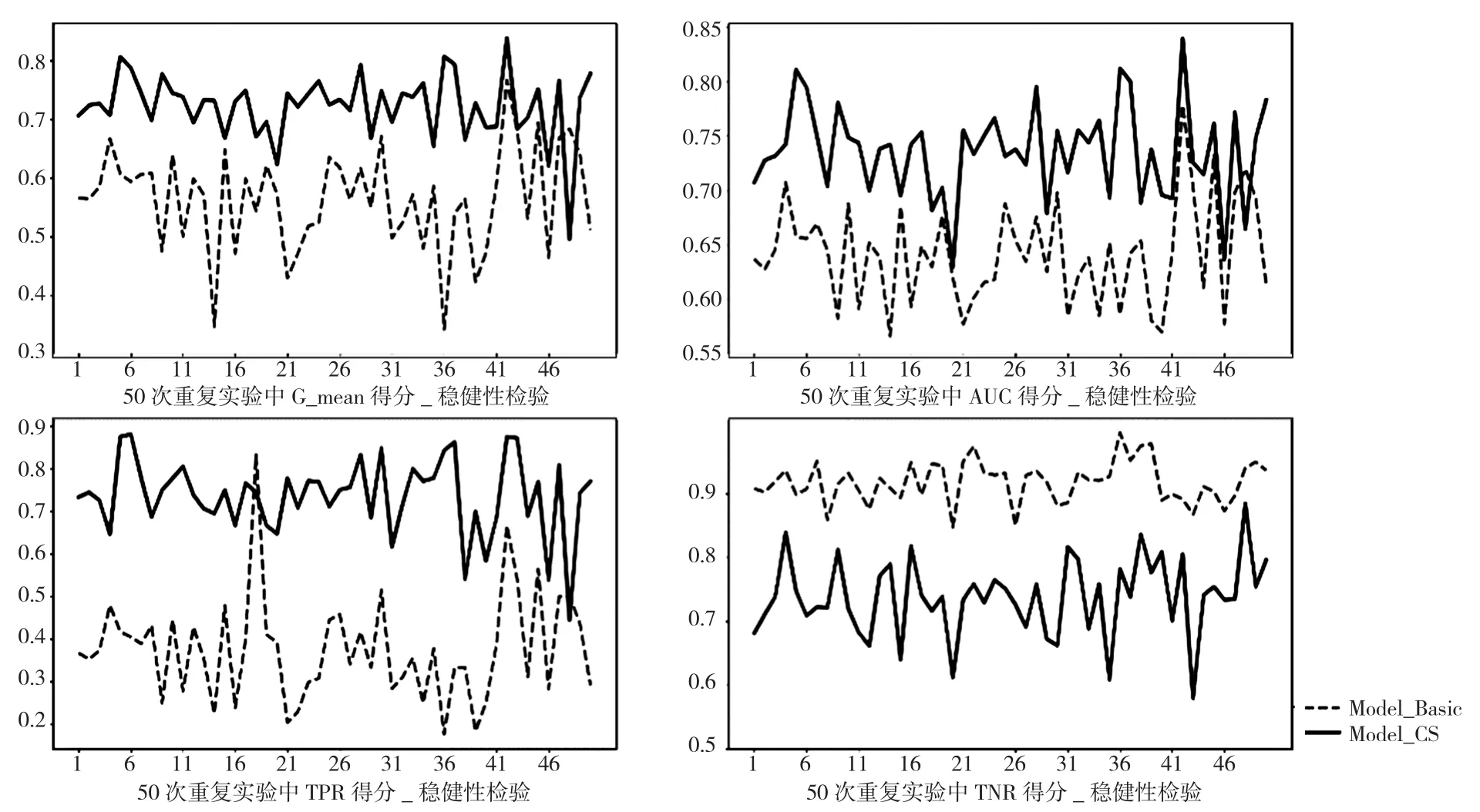
图2 稳健性检验过程中各指标得分

六、结论

本文以沪深A股制造业上市公司为研究对象，对财务预警中存在的特征冗余和数据分布不平衡问题进行了深入的研究。首先将双重显著性检验和主成分分析结合进行特征筛选和降维，之后将错分代价引入机器学习算法以构建代价敏感模型，并通过多次重复实验得到模型结果，最终证明代价敏感模型可有效应对财务预警领域中的不平衡问题，稳健性检验进一步证明了模型的可靠性。综合以上的实证研究，本文得出以下结论：第一，特征冗余作为金融数据的一个特点，须进行一定的特征筛选和变换来避免多重共线性对模型准确率产生影响；第二，在不平衡财务预警中，代价敏感模型通过引入不同类样本的错分代价，能够在模型构建过程中给予少数类更多权重，缓解传统模型的学习偏移问题，显著提升ST公司的分类准确度。

综上所述，本文构建的预警模型对上市公司预防财务困境的发生具有一定的借鉴意义，然而有关该问题的研究仍存在进一步的提升空间。如在处理不平衡问题时，可以考虑数据层面的重采样操作对模型整体效果的影响；另外，本文的工作是基于横截面数据开展的，在后续研究中可以考虑指标在时间上的相依性，并采用二元动态面板数据模型进行研究分析。