中间铰受力分析方法研究

2021-10-18赵丽霞

黑河学院学报 2021年9期

赵丽霞

(安徽理工大学，安徽淮南 232001)

在理论力学中，最重要的一项基本功就是对物体进行受力分析，准确而快速地画出物体受力图，如果在这一步中方法不当，轻则增加后续方程求解难度，重则直接导致最终结果的错误。光滑圆柱铰链约束作为机械工程中常见的约束类型，其受力分析对各个构件及系统受力情况的研究起至关重要作用。对于物体与物体间起连接作用的光滑圆柱铰链简称为中间铰，本文将依据中间铰的受力特点对其受力分析的方法做一个系统全面的研究，便于大家对号入座，根据具体问题具体分析，从而采用最简便、能简化后续求解过程的受力分析方法。

对于中间铰的受力分析，容易让人疑惑的问题包括销钉是否要单独取出画受力图；如果不单独分析将其与哪个连接的物体看成整体更好；不同的分析方法对结果有何影响等。下面就几种典型的情况做具体分析。为便于描述，文中将仅连接两个构件又不受其他力作用的中间铰称为简单铰；连接三个及以上构件的中间铰称为复杂铰。

1 中间铰的四种典型情况

1.1 简单铰的受力分析

图1所示构架中，C, D和E均为中间铰，且都是简单铰，绳索的一端固定在F点，另一端绕过滑轮E并与重物W连接，不计各构件的重量。首先单独对销钉D进行受力分析，其受到杆AB的力FD1x、FD1y和杆CE的力FD2x、FD2y，画出销钉D的受力图，并分别画出销钉D对杆AB、杆CE的力。由销钉受力图可知：销钉对两个构件的反作用力是等值、反向、共线的，将销钉附在任一构件上并不影响受力图的形式[1]。由此可得出结论：对于简单铰不必单独取出销钉分析，也无需指明是与哪个连接的构件看作整体，受力分析的结果不会受到影响。

图1 简单铰的受力图

1.2 复杂铰的受力分析

图2所示系统中，杆AD、杆BD、杆CD铰接于D处，杆BD与杆CD通过链杆HE连接，其中中间铰D为复杂铰，先取出销钉D的分离体进行受力分析，杆AD、杆BD、杆CD均对销钉D有力的作用，分别用一对正交分力表示为FD1x、FD1y、FD2x、FD2y、FD3x、FD3y。不难看出，此时销钉对各杆件的反作用力不再是等值、反向、共线的，所以，将销钉附在不同的构件上所得的受力图是完全不同的。将销钉D分别附在杆AD、杆BD、杆CD上，在D处的受力情况如下页图3所示。对比图2与图3可知，图3中铰链D处的受力情况更简单，未知力更少，由此可得出结论：对于复杂铰，为简化计算过程，一般不必单独画其受力图[2]，而是将销钉附在与其相连的构件上，但必须指明销钉是与哪个连接的构件看作整体，不同情况会使受力分析的结果会受到影响。

图2 复杂铰的受力图

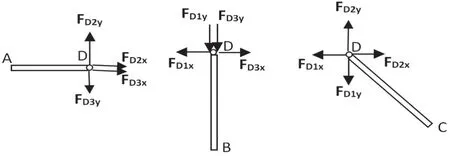
图3 复杂铰附在构件上的受力图

1.3 中间铰上作用集中力

前面分析的简单铰和复杂铰均没有集中力作用在铰链上，一旦出现这种情况该如何分析，又会得出怎样的结果，仍以实例分析。图4中的中间铰D上作用一集中力F，同时受到杆AD的力FD1x、FD1y和杆BD的力FD2x、FD2y，此时销钉D的施力物体多于两个，所以，销钉对各杆件的反作用力不再是等值、反向、共线的[3]，可以得出与情况二相同的结论，即将销钉附在与其相连的构件上，集中力F将跟随销钉作用在该构件上，同时，必须指明销钉是与哪个连接的构件看作整体，不同情况结果会截然不同。

图4 中间铰上作用集中力的受力图

1.4 中间铰连接二力构件

二力构件指只受两个力作用而平衡的构件，根据二力平衡公理，这两个力一定大小相等，方向相反，作用线共线[4]。在前面的分析中，关于构件给中间铰的力均是用一对正交分力来表示的，力矢量较多，受力图较复杂，如果中间铰连接的构件中存在二力构件，则可以通过寻找二力构件确定一些未知力的方位,从而减少未知量数目，达到简化计算的目的。例如图5所示的构架中，杆AC、BC铰接于C，中间铰C上作用一集中力F，系统中的杆AC、BC均为二力杆，销钉C给杆AC、BC的力必沿着杆件轴线方向，根据作用力与反作用力原理可确定杆件给销钉C的力，因此可作出中间铰C的受力图。

图5 中间铰连接二力构件

由图5可以看出，销钉C处的受力图比前面用正交分力表示的结果简单很多，同时通过对比杆AC含销钉和不含销钉两种情况的受力图，发现C处力矢量明显不同，此处学生可能会产生疑问，两种情况下A处受力不变，为什么C处却不同，实际上C处的力矢量F、F2可以合成为一个力F'1，并不违背力的平衡。所以为避免混淆，对于连接二力构件的中间铰上又作用集中力的情况，最好将销钉单独取出进行受力分析，这样更易指明受力和施力物体，不易发生错误[5]。由此得出结论：当中间铰连接二力构件时，要利用二力构件受力特点确定铰链处力的方位；铰链处又有集中力作用或中间铰为复杂铰时，不要将销钉附在二力构件上，而是要单独取其分离体或者将销钉附在其中不是二力构件的物体上进行分析。

2 结论

(1)对于简单铰不必单独取出销钉分析，也无需指明是与哪个连接的构件看作整体，受力分析的结果不会受到影响。

(2)对于复杂铰，为简化计算过程，一般不必单独画其受力图，而是将销钉附在与其相连的构件上，但必须指明销钉是与哪个连接的构件看作整体，不同情况会使受力分析的结果会受到影响。

(3)当中间铰上作用集中力时，将销钉附在与其相连的构件上，集中力F将跟随销钉作用在该构件上，同时，必须指明销钉是与哪个连接的构件看作整体，不同情况结果会截然不同。

(4)当中间铰连接二力构件时，要利用二力构件受力特点确定铰链处力的方位；铰链处又有集中力作用或中间铰为复杂铰时，不要将销钉附在二力构件上，而是要单独取其分离体或，将销钉附在其中不是二力构件的物体上进行分析。

3 具体应用

下面将利用上述结论对实际问题进行分析。已知构架尺寸如图6所示(尺寸单位为m)，不计各杆自重，载荷F=60KN。求A、E铰链的约束反力及杆BD、BC的内力。

图6 结构图

分析：在物体系统的平衡问题中，确定研究路线、选择合适的研究对象是首要考虑的。本题要求的是A、E铰链的约束反力，可以先取整个系统为研究对象，A、E处的约束反力为未知量，此时未知力数量为4，大于能列的平衡方程的个数，还需换其他研究对象。考虑本题还需求杆BD、BC的内力，可以取杆AB为研究对象，因为杆BD、BC为二力杆，铰链B为复杂铰且有集中力作用，因此，对AB进行受力分析时，要对销钉B单独进行分析。具体解题过程如下：

解：(1)取整个系统为研究对象，画受力图(见图7)