数学实验要有明确的目的与要求——以《平行四边形的面积》教学为例

文|翟运胜（特级教师）

【教学内容】

五年级上册“平行四边形的面积推导”。

【教学过程】

一、创设情境，制造认知冲突，引发探究需要

师：同学们，商场里都有停车场，这里有两种形状的停车位。（出示下图）谁来具体说说都是怎样的图形呢？

生：一种是长8米、宽4米的长方形；另一种是两条邻边分别是8米和4米的平行四边形。

师：这两种停车位的面积一样大吗？

（多数学生凭感觉认为两个停车场的面积是一样大的）

师：我们知道长方形的面积等于长乘宽，得到8×4＝32（平方米）。8和4是平行四边形相邻的两条边，那么平行四边形的面积会不会也是底边乘邻边呢？这是一个平行四边形框架，怎样做个小实验来证明平行四边形的面积是或者不是底边乘邻边呢？

生：把这个平行四边形拉一拉，然后再观察平行四边形的面积。

师：真好！请注意观察：在拉的过程中，平行四边形的底边和邻边有没有发生变化？面积呢？

生：在拉动的过程中，平行四边形的底边和邻边的长度始终不变，底边乘邻边是一个固定的数，但平行四边形的面积却在不断变化，由此可以得到平行四边形的面积不等于底边乘邻边。

学生填写实验结论，完成数学实验一：

?

【设计意图：课始创造问题情境，学生一般会认为这两个图形的面积一样大，受长方形面积计算方法的“迁移”，学生也多会认为平行四边形的面积计算也是底边乘邻边。顺着学生的思维，组织学生做数学实验，验证自己的猜想，这就使数学实验有了明确的目标。实验过程相对比较简单，便于学生从中发现实验结论，通过数学实验纠正了长方形面积计算带给学生在学习上的“负迁移”。】

二、动手实验，探索面积公式，培养理性精神

师：平行四边形的面积不等于底边乘邻边，那怎样计算平行四边形的面积？怎么做实验推导出平行四边形的面积计算公式呢？

生：把平行四边形剪拼成一个长方形，这个过程，面积是不变的。求转化后长方形的面积，也就求出了平行四边形的面积。

师：大家都想到了把平行四边形转化成长方形，我们只拿这样的一个平行四边形做实验，行不行？

生：不行，一个不够，要找各种不同形状的平行四边形。

师：老师给大家准备了一些平行四边形和需要用到的实验工具。想一想怎样来做这个实验呢？

生：通过剪拼，我们把这些平行四边形变成长方形。

师：再来明确一下实验要求。

1.剪一剪、拼一拼：把平行四边形转化成长方形。

2.贴一贴、填一填：按要求贴上图形，把表格填写完整。

3.比一比、想一想：比较前后两个图形，你有什么发现？

（学生汇报实验过程：都是沿着平行四边形的高剪，把平行四边形分成一个三角形与梯形，或者是分成两个梯形，然后拼成了一个长方形）

师：结合课件展示，是不是所有的平行四边形都能转化成长方形？例如下面这样的平行四边形。

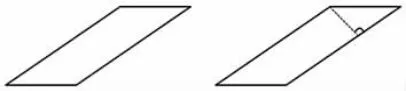
师：这条底边上的高在平行四边形的外面，不方便沿着这条高来剪，怎么办呢？

生：如果沿着一条底边上的高剪不方便时，就换个方向沿着另一条底上的高剪，都能把一个平行四边形分成一个三角形与一个梯形。

师：看来任意一个平行四边形都可以通过剪拼的方式转化成长方形。谁来回答这三个问题？

1.转化成的长方形和平行四边形面积相等吗？

2.长方形的长和宽与平行四边形的底和高有什么关系？

3.根据长方形的面积公式，怎样求平行四边形的面积？

（学生小组内交流，个别汇报）

师：如果用字母S表示平行四边形的面积，a表示底，h表示高，那么平行四边形面积的计算公式可以怎样表示呢？

生：S＝a×h。

学生填写实验结论，完成数学实验二：

实验目的推导平行四边形的面积计算公式。实验工具四个不同形状的平行四边形（有格子）、剪刀、胶水等。实验方法1.剪一剪、拼一拼：把平行四边形转化成长方形。2.贴一贴、填一填：按要求贴上图形，把表格填写完整。3.比一比、想一想：比较前后两个图形，你有什么发现？学生交流：用什么具体方法把平行四边形转化成长方形？问题思考：1.转化成的长方形和平行四边形面积相等吗？2.长方形的长和宽与平行四边形的底和高有什么关系？3.根据长方形的面积公式，怎样求平行四边形的面积？实验结论平行四边形的面积＝底×高实验交流

【设计意图：《数学课程标准（2011年版）》中明确指出“学生应当有足够的时间和空间经历观察、实验、猜想、计算、推理、验证等活动过程”，因此教师在教学中要能够沉下心来，先暂时舍弃一些练习时间，通过《实验单》，使学生具有明确的实验目标意识，让学生有足够的时间与空间分小组合作实验，表达实验方法、实验感受与实验结论，注重培养学生的主体意识，从而逐步积累丰富的数学活动经验。】

三、巩固练习

1.基本练习，巩固面积公式。

（学生独立完成计算，并汇报）

师：你能想象出第三幅图剪拼后形成的长方形是什么样子吗？

生：剪拼形成的长方形长是15米，宽是8米。

师：其面积怎样算？如果以10米的边为底，对应的高是多少？

生：15×8=120（平方米），120÷10=12（米）。

师：如果沿着这条高来剪拼，所形成的长方形是什么样子呢？

生：剪拼形成的长方形长是10米，宽是12米。

2.前后呼应，解决实际问题。

师：回到课开始的停车位问题，现在这个平行四边形停车位的面积能算吗？

生：不能算，因为没有告诉高的数值，条件不够，所以不能算。

课件出示：

师：它的面积是多少？

生：3×8＝24（平方米），或者4×6＝24（平方米）。

小结：找到底边所对应的高，平行四边形有两组不同的底和高，大小不同，但计算结果相同。

【设计意图：与课开始的停车位问题前后呼应，使学生看到实验推导出来的平行四边形面积计算公式成功解决了“停车位大小”这个现实问题，这种解决真实问题后的欣喜感是学生产生学习动力的不竭源泉，并在这个过程中培养了学生求真务实的理性精神。】

3.沟通联系，建立知识框架。

师：现在我们知道平行四边形的面积等于底乘高，那么长方形是平行四边形吗？

生：长方形是平行四边形。

师：那长方形的面积为什么是底边乘邻边呢？怎样做个小实验？

生：拉动平行四边形框架使之成为长方形，观察长方形的底边与邻边。

师：拿出实验工具，我们来动手做一做吧。

生：在拉动的过程中，平行四边形的高在不断增加，当拉成长方形时，长方形的宽就和高重合了，所以长方形的面积并不是底边乘邻边，仍然是底乘高。

生：我明白了，其实这里的宽就是高，并不是底边乘邻边。

学生填写实验结论，完成数学实验三：

把平行四边形拉成长方形，体会邻边的变化过程。实验结论长方形的面积＝底×高实验目的长方形的面积为什么是底边乘邻边？实验工具活动的平行四边形框架。实验方法

【设计意图：通过再次做拉动平行四边形框架的数学实验，使学生深刻认识到长方形的宽就是高，从而把长方形的面积计算纳入平行四边形的面积计算公式中，体会数学知识的本质，构建知识体系，感受“变”与“不变”的辩证思想。】

四、回顾总结，畅谈收获（略）