《平行四边形的面积》教学与反思
2016-09-26徐素君
徐素君
【中图分类号】G623.5 【文献标识码】A 【文章编号】2095-3089(2016)20-0080-02
平行四边形面积的计算是在学生学习了面积的概念、长方形、正方形的面积的计算方法和平行四边形的认识的基础上教学的,平行四边形面积公式推导方法的掌握,对学习后面三角形、梯形面积公式具有重要作用。本节课的教学环节设计突出以下三个方面:1.重视原有认知基础对新知识的促进作用。教学中从学生的生活经验和已有的知识出发,唤起学生对相关知识的记忆,通过制造认知冲突和分析比较,激发学生探索的欲望,积极引导学生探讨平行四边形与已学长方形的之间的联系。 2.加强动手操作活动,使学生亲历“做数学”的过程。让学生经历平行四边形面积计算公式的探索过程是本节课的重要目标,本节课在平行四边形面积公式推导这一环节中,引导学生通过动手操作、合作学习、相互交流等学习方式去主动发现平行四边形的面积公式。在探究过程中,学生积极动手、动脑,把平行四边形转化成长方形,并通过观察,发现长方形与平行四边形的内在联系,在此基础上推导出平行四边形的面积计算公式。3.注重练习设计的层次性,加强对公式的运用和实践能力的培养。本节课在练习反馈,巩固深化环节上设计了几个练习,让学生用自己推导的面积计算公式解决平行四边形面积计算的问题,通过练习沟通图形间的相互联系,使学生对面积计算公式理解得更加深刻。
教学内容:西师版教材五年级上册第85页~87页例1、例2及相应的练习。
教学目标:
1.利用方格纸或割补等办法,探索并掌握平行四边形的面积计算公式,会利用这个公式计算图形面积。
2.能主动应用原来掌握的相关知识探索新知识,在主动探索知识的过程中获得成功体验。
3.在探索知识的过程中培养学生的合作意识和多向思维的能力。
教学重点:研究并推导平行四边形面积的计算公式并能正确运用。
教学难点:理解通过转化推导出平行四边形面积公式的方法和过程。
教具准备:长方形、平行四边形卡片、多媒体课件等。
学生准备:平行四边形卡片、剪刀等学具。
教学过程:
一:创设情境,引发探究。
1.出示校园一角图片,请同学们认真观察图片是哪里?从图中你看到了哪些图形?
2.我们已经学习过哪些图形的面积计算?在剩下的几种图形里面,谁的特征最接近长方形和正方形?平行四边形有哪些特征?会计算它的面积吗?揭示课题并板书:平行四边形的面积
二、实践操作,探究新知
(一)面积公式的推导
教学例1。
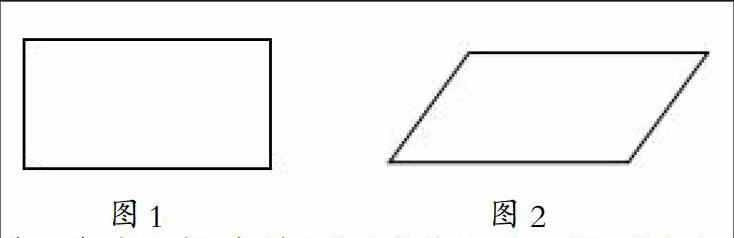
比一比,哪个图形的面积大?
图1 图2
(1)看一看,想一想,怎样才能比较出这两个图形的大小呢?
(2)把这两个图形放在方格纸里数一数,比一比。请大家仔细观察方格纸里的两个图形,注意这里的每个小方格表示1平方厘米,不满一格的都按半格计算,数一数它们的面积各是多少?长方形的面积是多少?平行四边形的面积是多少?你是怎么数的?
(3)请同学们想一想,在数方格的过程中有没有更方便的办法?引导学生通过思考得出:可以找到长方形的长和宽计算出面积,可以把平行四边形转化成长方形来求面积。
(4)猜猜看平行四边形的面积怎样计算?
(5)你能把平行四边形转化成长方形吗?请大家借助手中的平行四边形卡片、剪刀等学具动手试一试。
(6)学生动手操作后汇报展示转化方法。
(7)小组讨论,分析比较,推导公式,得出结论。
请同学们比较转化成的长方形和原来的平行四边形思考这两个问题:
1.长方形的长和宽与平行四边形的底和高有什么关系?
2.怎样用长方形的面积公式推导出平行四边形的面积公式?
学生讨论后得出:平行四边形的底与长方形的长相等,平行四边形的高与长方形的宽相等,平行四边形的面积等于长方形的面积。
课件出示: 长方形的面积= 长 × 宽
平行四边形的面积= 底 × 高
(二)面积公式的应用
1.出示例2。
(1)同学们能用平行四边形面积计算公式计算出这两个平行四边形的面积吗?想想在计算面积前先要知道什么?
(2)请同学们分别计算出这两个图形的面积。
(3)学生计算后汇报,并用数方格的方法检验结果。
2.第87页例2下面的试一试。
三、练习反馈,巩固深化。
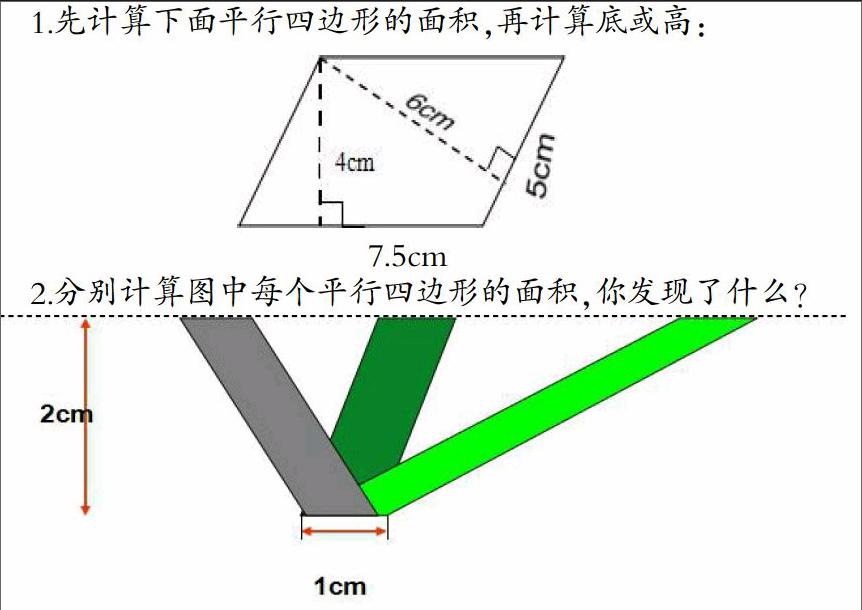
1.先计算下面平行四边形的面积,再计算底或高:
2.分别计算图中每个平行四边形的面积,你发现了什么?
学生计算后得出:等底等高的平行四边形的面积相等
3.猜一猜:
学校要建一个面积是12平方米的平行四边形花坛,这个花坛的底和高可能是多少?有多少种可能?每种可能都实际吗?
四、总结全课
通过这节课的学习你有什么收获?
教学反思:
教学完《平行四边形的面积》这一课自己感触颇多,有成功的喜悦,也有不足的遗憾,反思这节课,具体概括为以下几点:
第一,创设问题情景,引起矛盾冲突,激发了学生的学习兴趣。本节课开始,我出示学生熟悉的学校全景图片,通过观察从图中找出学过的平面图形,并复习有关知识唤起学生的知识回忆,再通过“你能比较出两个图形的面积吗?”的问题,激发了学生的学习兴趣,使其积极投入到学习活动中来。
第二,渗透“转化”的思想。“转化”是数学学习和研究的一种重要思想方法,在本节课的教学中,通过引导学生用数方格的方法比较平行四边形和长方形的大小后,并没有就此结束,而是巧妙设问:请同学们想一想,在数方格的过程中有没有更方便的办法?引导学生通过观察思考发现:可以找到长方形的长和宽计算出面积,还可以把平行四边形转化成长方形来求面积。这一发现为学生进一步的的探究活动打下了坚实的基础。教学过程由浅入深,由易到难,由具体到抽象,由感性认识到理性认识,步步深入,紧扣主题。巧妙渗透“转化”的思想,让学生自己发现学习的方法,学会利用旧知识解决新的问题,形成积极主动的探究氛围。
第三,我的遗憾。本节课还有一些不足之处,对课堂上学生可能出现问题的预设不够充分。如在转化图形时,当时学生回答:“我认为它们的形状发生了变化,但周长和面积都没有变。”时,我在课前只是对形变积不变有预设,但未通过数方格检验加以证明,对形变周长是否变化更未做出预设并引导学生探究,学生的认知是不完善、不深刻的。这些不足将在今后的教学实践中不断完善。
