复变函数斜轴椭球变换法的衔接应用
2021-09-13姚德新
杨 力,姚德新
(1.兰州交通大学 测绘与地理信息学院,甘肃 兰州 730070;2.地理国情监测技术应用国家地方联合工程研究中心,甘肃 兰州 730070;3.甘肃省地理国情监测工程实验室,甘肃 兰州 730070)
随着长大线路工程建设需求越来越多,对长大线路工程控制网的精度提出越来越高的要求。控制长度投影变形是长线工程施工质量的重要保证。文献[1-5]提出法截面子午线高斯投影,有效的减小测区到中央子午线的距离,控制长度投影变形,解决高斯投影频繁换带、精度不高等问题,但该方法计算过程复杂、参数设置繁琐。文献[6-7]提出斜轴变形椭球高斯投影,利用空间直角坐标的优越性及便利性大大减小测区的高斯投影横坐标,有效降低高差带来的影响。文献[8-10]提出采用大椭圆线椭球高斯投影,优化计算,数据处理效率高,同样适用于长线工程。在长度投影变形分析中,满足投影变形不大于10 mm/km的条件下,测区平均高程大于63.71 m时需考虑由高程引起的长度变形,测区距中央子午线距离大于28.5 km时,需考虑投影引起的长度变形。但是文献[2-10]所提出的多种方法在线路经过地势复杂区域时,线路转折大、高差大,导致部分测区边缘距斜轴椭球中央子午线较远平均高程大的问题,此时一个工程椭球并不能满足综合投影变形不大于10 mm/km的要求,需对线路进行平面、高程分段处理。文献[11]提出交点法线重合的方法,面对转折大的长线工程分成多段子午线法截面椭球进行平面衔接。文中在斜轴变形椭球高斯投影理论的基础上提出复变函数斜轴椭球变换法高斯平面坐标微分公式,构建斜轴椭球变换前后高斯平面坐标转换模型,并通过实际铁路工程数据验证该模型在坐标系的衔接,以及建立高精度工程控制网中的优越性与适用性。
1 复变函数高斯平面坐标的微分公式推导
高斯投影正解的非迭代复变函数表示[12-13]:
q=arctanh(sinB)-e·arctanh(e·sinB),
w=q+il,
φ=arcsin(tanh(w)),
z=x+iy=a(j0φ+j2sin2φ+j4sin4φ+
j6sin6φ+j8sin8φ+j10sin10φ),
x=Rez,y=lmz.
(1)
式中:q为等量纬度;w为投影前等量纬度与经差组成的复变量;z为高斯投影后平面纵横坐标组成的复变量,其中x为纵坐标,y为横坐标;B,l为大地纬度,经差;e为第一偏心率;a为椭球长半轴。Re为复数实部,Im为复数虚部。
复变量z分别对参数(a,e,B,l)求微分:
(2)
中间量偏导数:
(3)
(4)
(5)
(6)
矩阵中各偏导数:
j6sin6φ+j8sin8φ+j10sin10φ),
(7)
2j2cos2φ+4j4cos4φ+6j6cos6φ+8j8cos8φ
+10j10cos10φ)],
(8)
6j6cos6φ+8j8cos8φ+10j10cos10φ),
(9)
6j6cos6φ+8j8cos8φ+10j10cos10φ).
(10)
2 椭球变换法大地坐标与高斯坐标微分公式
2.1 椭球膨胀法大地坐标与高斯坐标微分公式
椭球膨胀法:椭球中心、轴向、椭球偏心率e保持不变,椭球长短半轴发生变化。椭球长半轴变化da=a1-a0。采用高程直接补偿法,选取da=△H0。
膨胀椭球大地坐标微分公式[2]:

(11)
膨胀椭球高斯坐标微分公式:
(12)
2.2 椭球平移法大地坐标与高斯坐标微分公式
椭球平移法:将椭球以椭球中心平移,不改变椭球的轴向、长半径、偏心率、尺度。
平移椭球大地坐标微分公式[2]:

(13)
平移椭球高斯坐标微分公式:
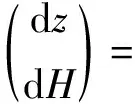
(14)
2.3 椭球变形法大地坐标与高斯坐标微分公式
椭球变形法:椭球的长半径、偏心率改变,而不改变椭球的轴向、中心、尺度。
变形椭球大地坐标微分公式[2]:

(15)
变形椭球高斯坐标微分公式:
(16)
3 高斯平面坐标衔接模型
根据复变函数高斯平面坐标微分公式与椭球变换法大地坐标微分公式构建高斯平面坐标衔接模型:
(17)
式中:z1,z2为椭球变换前后高斯平面坐标复变量;dx,dy为复变函数高斯平面坐标微分公式计算的高斯平面坐标的位移量;(x1,y1)和(x2′,y2′)为椭球变换前后的高斯平面坐标。
4 算例分析
文中数据来源于文献[2,6]中的算例分析。根据“某铁路控制测量成果报告”的内容,正线方案长约500 km,测区位于86°00′E~95°30′E,36°00′N~42°00′N,线路海拔高程最大为3 163.6 m,最小为2 797.8 m[2,6]。11个测站点在基础椭球E0(CGCS2000)上的线路走向如图1所示。由于篇幅所限,文中选取较好表达线路走向的6个测站点(1、7、8、9、10、11号点)数据进行算例分析。依据斜轴变形椭球高斯投影理论,利用最小二乘法,空间坐标系旋转,将基础椭球E0变换到斜轴椭球E1上。6个测站点在斜轴椭球E1上的大地坐标以及在E1椭球参数下的高斯平面坐标见表1。斜轴椭球E1长半轴a1为6 378 137 m,偏心率e1为0.058 134 977 515 3。
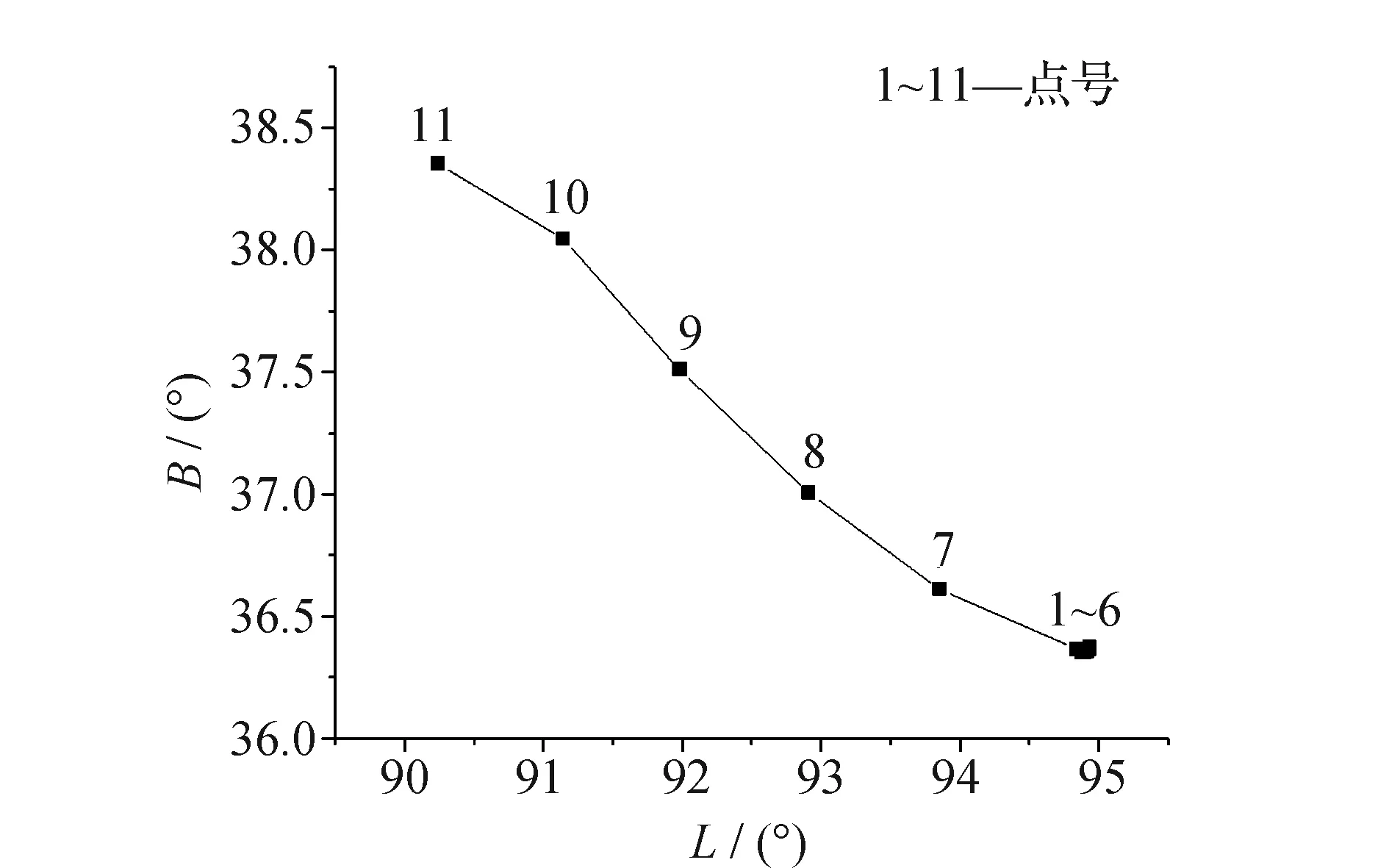
图1 线路走向测点分布图
4.1 斜轴膨胀椭球
在斜轴椭球E1的基础上,根据椭球膨胀法[14-15]将斜轴椭球E1膨胀到E2椭球,见图2。各点在E2椭球上的投影面高程、大地坐标、高斯平面坐标(x2,y2)以及长度投影变形,见表2。通过复变函数高斯平面微分公式计算高斯平面经椭球变换前后高斯平面坐标位移量(dx,dy),高斯平面坐标衔接模型计算膨胀后高斯平面坐标(x2′,y2′)。通过(x2,y2)与(x2′,y2′)的较差进行精度检验,x2坐标误差小于15.5 mm,y2坐标误差不大于0.07 mm,见表3。

图2 斜轴膨胀椭球及高斯平面坐标

表1 E1大地坐标与高斯平面坐标
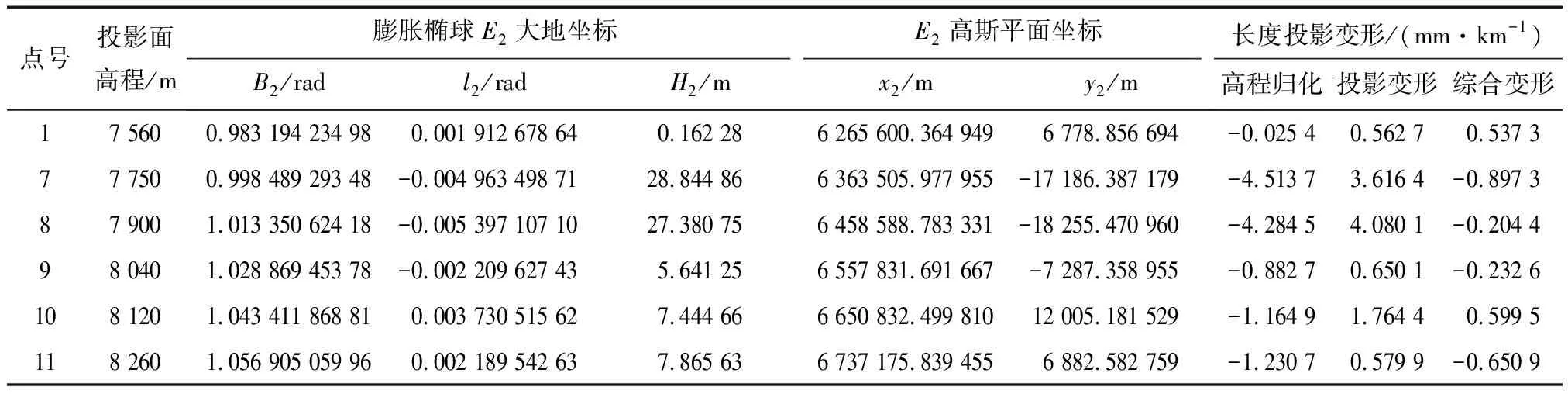
表2 斜轴膨胀椭球高斯投影
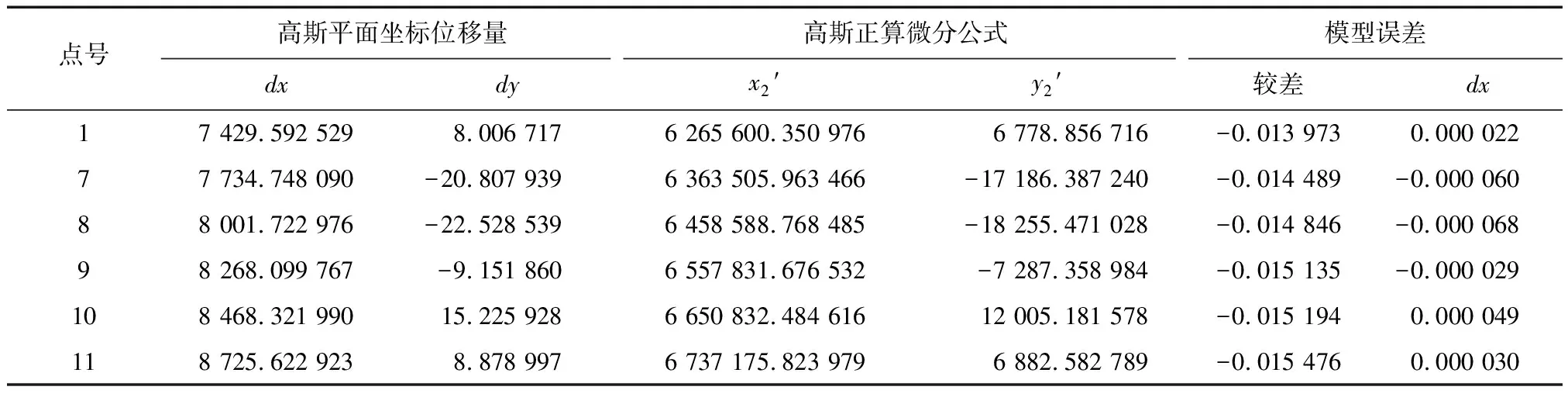
表3 斜轴膨胀椭球高斯平面坐标衔接模型误差分析 m
面对地势复杂地区线路高差大,会导致长度投影变形高程归化改正超限的情况,需根据不同的投影面高程进行膨胀。选取1号点,进行不同投影面高程椭球膨胀,根据投影面高程的差值可计算椭球膨胀前后高斯平面坐标位移量。膨胀椭球投影高程面高差小于100 m时,椭球膨胀前后高斯平面衔接模型误差小于0 mm;投影高程面高程差值为9 000 m的时候,椭球膨胀前后高斯平面衔接模型误差小于0.026 mm,见表4。在满足投影变形的条件下,选择合适的高程投影面,不同投影面高程膨胀椭球高斯平面坐标可以两两转换。

表4 斜轴椭球不同高程投影面高斯平面坐标衔接模型误差分析 m
4.2 斜轴平移椭球
利用椭球平移法[14-15]将斜轴椭球E1平移到E3椭球,见图3。E3椭球参数与斜轴椭球E1一致。此时点在E3椭球上的大地坐标、高斯平面坐标(x3,y3),长度投影变形见表5。通过复变函数高斯平面微分公式计算经椭球变换前后高斯平面坐标位移量dx,dy,高斯平面坐标衔接模型计算平移后高斯平面坐标(x3′,y3′)。通过(x3,y3)与(x3′,y3′)的较差进行精度检验,高斯平面坐标衔接模型x坐标误差不大于1.7 mm,y坐标误差不大于10.9 mm,见表6。
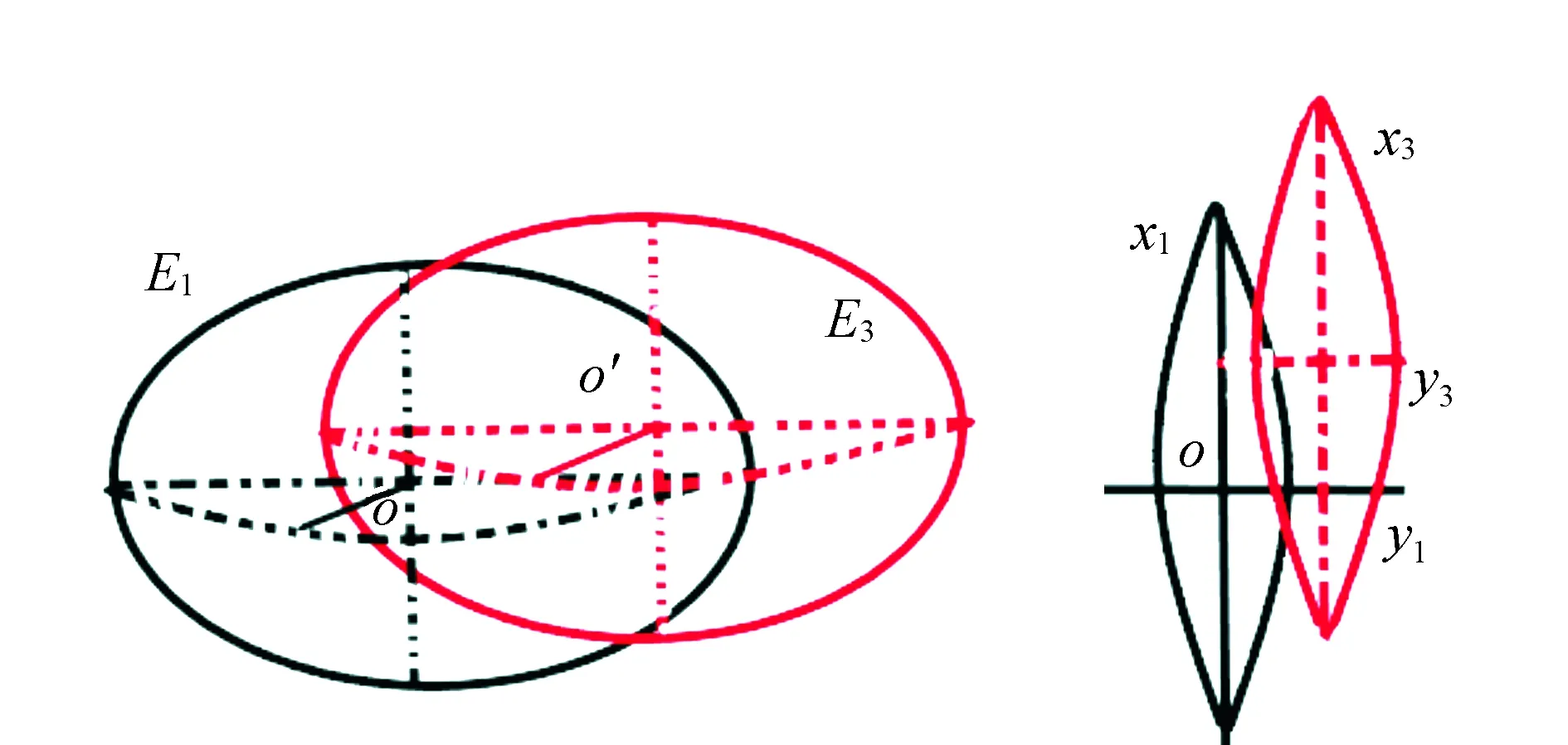
图3 斜轴平移椭球及高斯平面坐标

表5 斜轴平移椭球高斯投影

表6 高斯平面坐标衔接模型误差分析m
4.3 斜轴变形椭球
利用椭球变形法[14-15]将斜轴椭球E1变形到E4椭球,见图4。点在E4椭球上的投影面高程、大地坐标以及高斯平面坐标(x4,y4),长度投影变形小于10 mm/km,见表7。通过复变函数高斯平面微分公式计算经椭球变换前后高斯平面坐标位移量dx,dy和高斯平面坐标衔接模型计算平移后高斯平面坐标(x4′,y4′)。通过(x4,y4)与(x4′,y4′)的较差进行精度检验,高斯平面坐标衔接模型x坐标误差小于16 m,y坐标误差不大于0.026 mm,见表8。
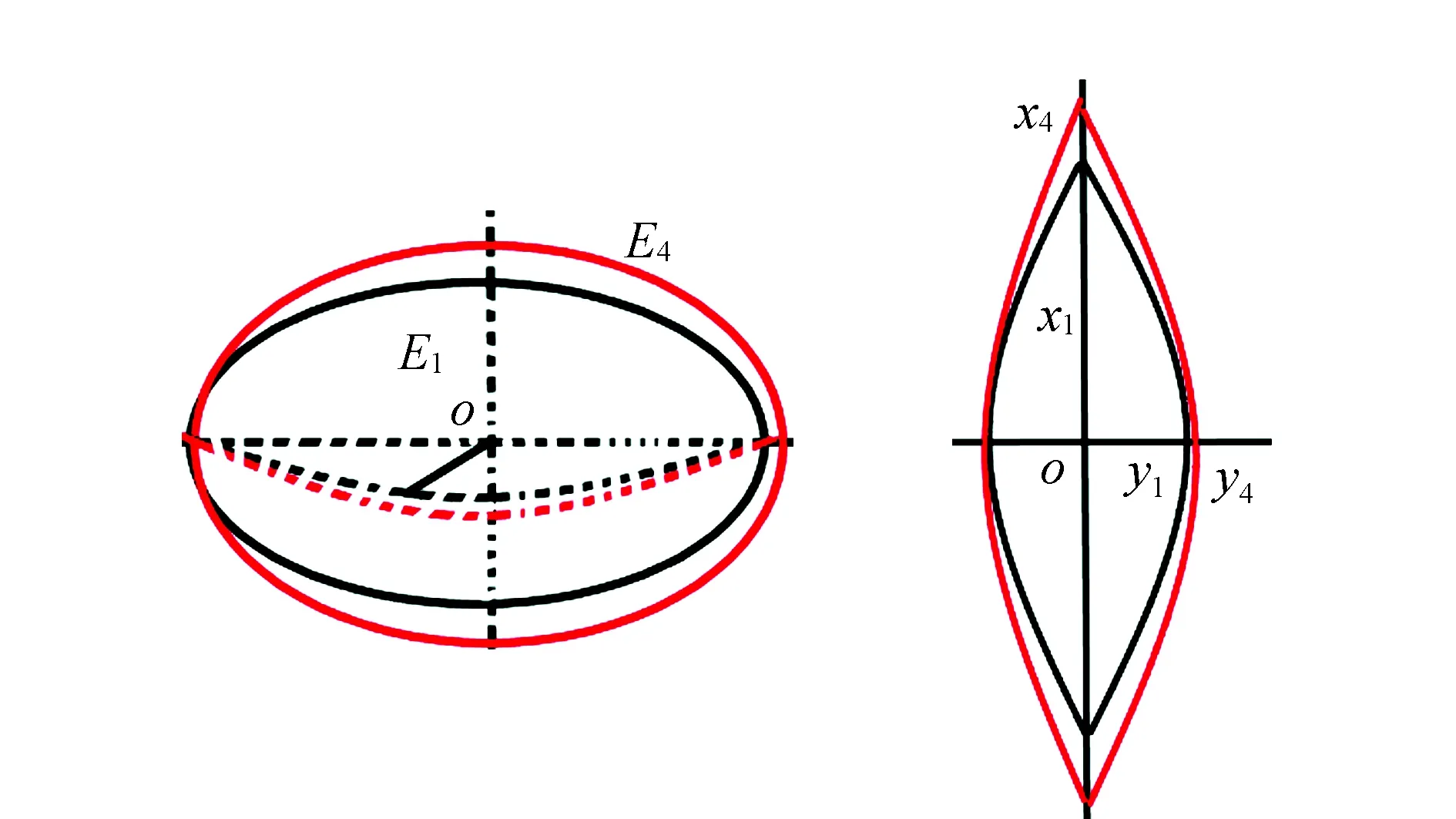
图4 斜轴变形椭球及高斯平面坐标

表7 斜轴变形椭球高斯投影
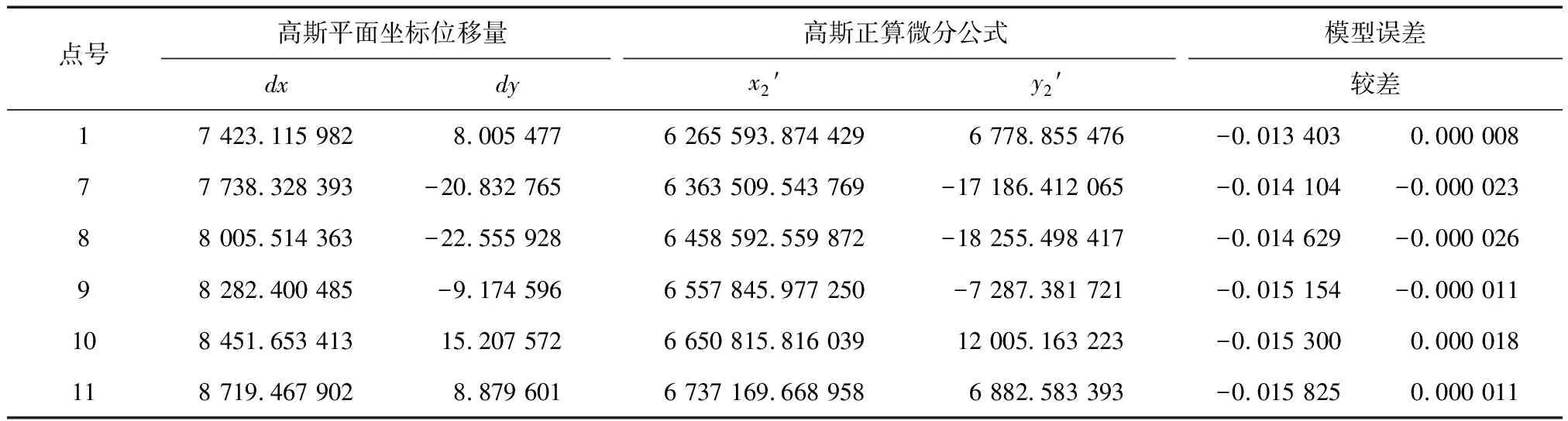
表8 高斯平面坐标衔接模型误差分析m
5 结束语
文中以复变函数求偏导数推导高斯平面坐标微分公式,构建高斯平面坐标转换模型,并结合实际铁路工程数据进行分析,得出如下结论:
1)高斯平面坐标衔接模型在斜轴平移椭球中精度最高误差小于10.9 mm,其次是斜轴膨胀椭球误差小于15.5 mm,斜轴变形椭球最大误差为16 mm。由误差分析可知,通过误差改正模型可将高斯平面坐标衔接模型的精度进一步提高。同时涉及椭球参数变化量大小、椭球变换基准点的选取、提高投影面高程精确值等。
2)面对转折大、高差大的长线路工程,所构建的多个工程椭球利用椭球变换参数值即可计算椭球变换前后高斯平面的坐标位移量,并可进行椭球变换前后的高斯平面坐标衔接。
3)较大的投影面高程椭球膨胀,高斯平面衔接模型误差小于0.026 mm,在满足投影变形的条件下,选择合适的高程投影面,不同投影面高程膨胀椭球高斯平面坐标可以两两转换,验证高斯平面坐标衔接模型的正确性与优越性。
4)利用Mathematica数学软件推导复变函数高斯平面微分公式以及构建高斯平面坐标衔接模型,可编制相关软件,投入工程使用。
