一种改进的病态问题截断奇异值方法
2021-09-13李明樾
谢 建,李明樾
(1.湖南科技大学 煤炭资源清洁利用与矿山环境保护湖南省重点实验室,湖南 湘潭 411201;2.广西交通职业技术学院 路桥工程系, 广西 南宁 530023)
病态问题在GNSS快速定位[1],回归分析[2],卫星重力向下延拓[3-6],PolInSAR植被参数反演[7]等测绘领域广泛存在,严重影响参数估计的精度和可靠性。病态性产生的原因可能是参数之间存在相关关系,或者观测值采样不足,或者观测结构不合理[8]。处理病态性的方法主要包括岭估计、正则化方法、截断奇异值或修正奇异值方法、附加等式或不等式约束、将参数视为随机变量的Bayes方法或最小二乘配置方法[3]。Bayes方法和最小二乘配置需要假设参数的先验统计信息,在实际应用中一般不容易预先得到。当正则化矩阵为单位阵时,岭估计和单参数正则化解具有相同的形式。正则化方法是在残差加权平方和的最小二乘准则上,加入参数线性组合的最小范数,然后确定合适的因子(正则化参数)来调节数据的拟合量和平滑量[9-10]。线性组合方法一般根据参数的特点,选择一阶或者二阶差分操作算子[11]。当设计阵的零空间和正则化矩阵的零空间不相交时,能得到唯一的正则化解。截断奇异值方法是将系数矩阵进行奇异值分解后,将严重扩大参数方差的小奇异值截去,从而得到可靠的解。而修正奇异值方法是对小的奇异值进行修正改善系数的病态性[6]。截断奇异值方法简单明了,仅需要考虑小奇异值对方差的影响,从而在大地测量领域得到广泛关注。截断奇异值方法的关键问题在于截断参数的选取。常用的有L曲线法、广义交叉核实(GCV)法、F假设检验法和均方误差极小化方法[4]。林东方提出了顾及截断偏差影响的截断奇异值截断参数确定方法,并与上述常用方法进行比较[7]。目前的研究大部分聚焦于截断参数的选取本身,而对病态问题的奇异值解的最优化准则缺乏研究。
在正则化方法中,对于某些实际问题,附加合理的正则化矩阵能得到比单位正则化矩阵更好的结果[11]。文中通过对截断奇异值理论分析发现,对设计矩阵进行奇异值分解后,删除较小的奇异值及对应的奇异值向量,组成新的秩亏系数矩阵后,截断奇异值解就是秩亏观测系统下的最小范数最小二乘解。为了改善截断奇异值估计的精度,借鉴正则化矩阵的选取方法,将最小范数条件‖x‖2最小替换为参数线性组合的最小范数条件‖Lx‖2最小,并在此条件下给出改进的截断奇异值分解方法的参数估计表达式,提出用L曲线法确定截断参数。数值模拟实验表明,修正的截断奇异值分解算法能得到比截断奇异值方法在均方误差意义下更好的解。
1 截断奇异值分解及其等价形式
1.1 最小二乘解的奇异值分解表达式
测量数据处理中,一般是将观测值表示成待定参数的线性或线性化函数,即经典的Gauss-Markov模型:
y=Ax+e,
(1)
(2)
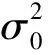
A=UΛVT.
(3)
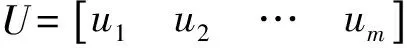
在最小二乘准则eTPe=min下,Gauss-Markov模型的最小二乘参数估值为:
(4)
将奇异值分解表达式(3)代入最小二乘估计式(4),可以得到最小二乘解的奇异值表达式及相应的方差矩阵为[4]:
(5)
(6)
1.2 病态问题的截断奇异值方法
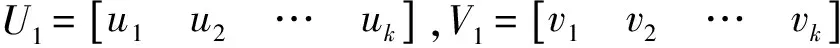
minxTx,
(7)
s.t.φ(x)=(Akx-y)T(Akx-y)=min.
(8)
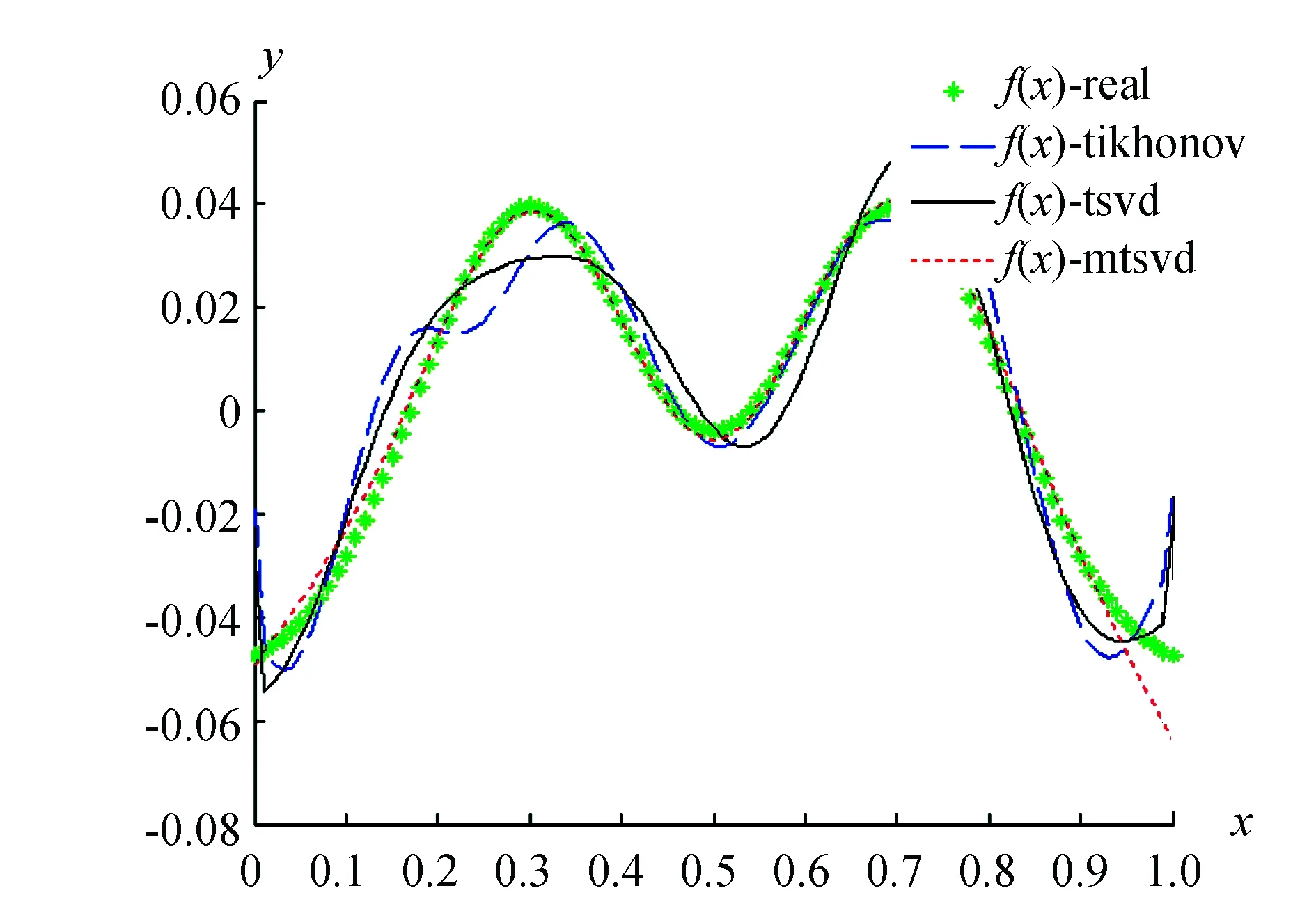
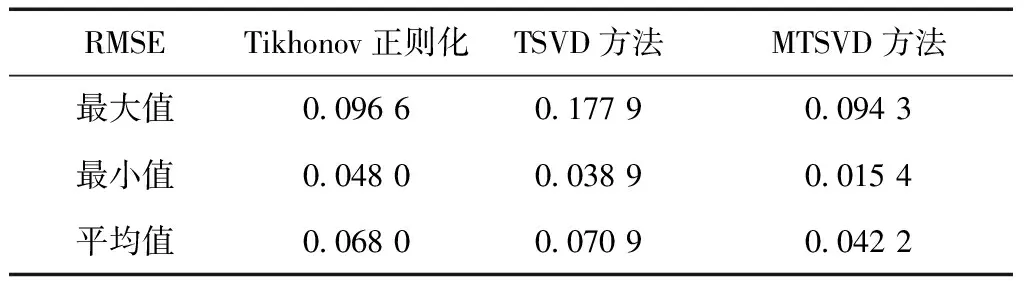
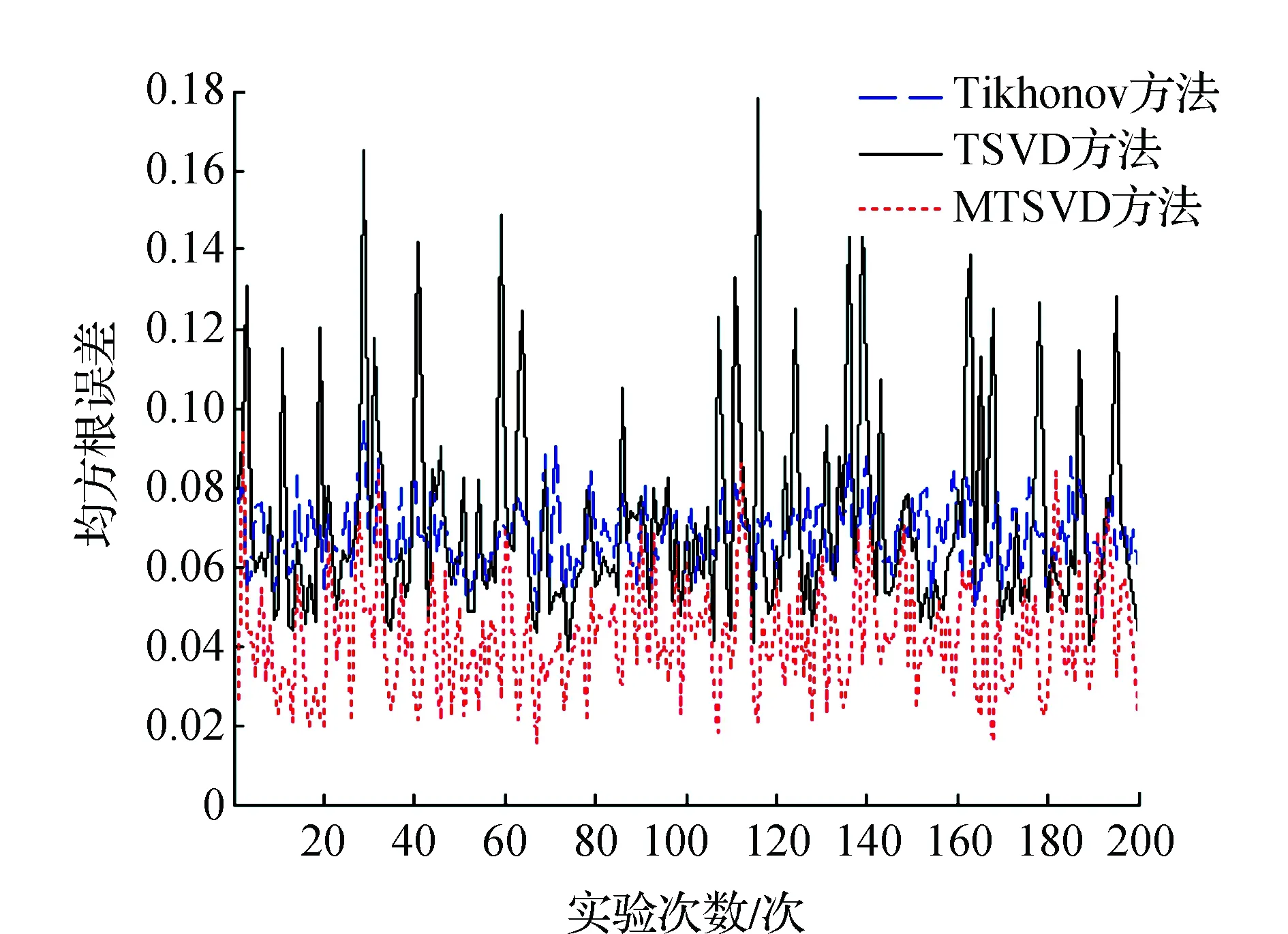
由于rank(Ak)=k (9) (10) 具体证明见文献[12]和文献[13]。另外,由奇异值分解定理有[12]: (11) 将式(11)代入式(10),可以得到最小范数最小二乘解的奇异值分解形式为: (12) 从式(12)可以看出,将系数阵A中的小奇异值删除构造近似矩阵Ak,将Ak代替式(1)中的设计矩阵,得到的最小范数最小二乘解与式(5)比较, 相当于截去对应于最小二乘解特征值较小部分的解分量,从而达到稳定解的目的。与正则化估计和岭估计类似,截断奇异值解比最小二乘解具有更小的均方误差[4],因此成为解病态问题的一种重要方法。令V2=[vk+1vk+2…vn],U2=[uk+1uk+2…un],Λ2=diag[λk+1λk+2…λn],对式(12)求期望,有: (13) 可见,TSVD解不再是无偏估计量,其偏差为: (14) 为了获得稳定且质量可靠的参数估值,关键在于确定合适的截断参数。若k值过大,则部分小奇异值未删除,解不稳定。反之,则丢弃有用的观测信息从而损失解的精度。这与Tikhonov正则化参数的选取原理相同,过小的正则化参数达不到稳定解的作用,而过大的参数造成过度平滑。L曲线法是确定正则化参数的有效方法,它能合理地平衡病态模型的拟合部分和平滑部分[14-16]。对于正则化解: (15) (16) (17) 由1.2节易知,截断奇异值方法减弱病态性的方法与Tikhonov正则化方法类似,都是通过附加参数的范数最小条件,取观测残差的范数达到最小,从而求得最小范数最小二乘解。Tikhonov正则化解式(15),实际上是条件极值问题的解[14]。 (18) 式中:ε是一个很小的正数。根据约束极值问题的Kuhn-Tucker条件,式(18)等价于求下列函数的极小值: (19) 式中:α是Lagrange乘子(即正则化参数),应满足非负条件。正则化矩阵L可以取不同的形式。当L=I(表示单位矩阵)时,表示附加参数的范数最小条件。当已知参数间的某些特点时,常用一阶或二阶差分算子作为正则化矩阵,能得到比单位矩阵作为正则化矩阵更好的估计结果[11]。在重力场确定中,一般用Kaula准则作为正则化矩阵,它是以阶方差模型或先验重力场模型确定的信号方差作为对角元素。类似地,将式(8)的目标函数进行如下修正,从而建立起改进的奇异值算法的目标函数为: (20) (21) 与1.2节相同,首先求得式(21)的通解为式(9),将其代入式(20)有: (22) 可以证明,当N(Ak)∩N(L)=0,即Ak和L的零空间线性无关时,目标函数式(22)极小条件下的t值为[13]: t=-(LP)+Lg. (23) 将式(23)代入式(9),可以得到x的极小值为: (24) (25) (26) MTSVD解的偏差为: (27) 第一类Fredholm积分方程是典型的病态问题。在大地测量中,由卫星重力数据恢复局部重力场实质上就是对Fredholm积分方程的解算。该方程的一般形式为: (28) 其中,z(y)表示含有误差的观测值;K(x,y)是已知的核函数;f(x)是待定的函数,由观测值和核函数通过积分方程来估计。本文算例采用文献[5]提供的核函数和精确已知的函数f(x)来构造病态模型。其中, (29) K(xi+1,yj)f(xi+1))Δx. (30) 式中:j=1,2,…,401。式(30)可以进一步化为: (31) 首先绘制f(x)的真实曲线f(x)-real,见图1。可以看到该曲线呈二次抛物线形状,可以采用二阶离散差分算子来表达其先验信息,它的具体形式为: (32) 图1 一次实验中3种方法的计算结果比较 在大地测量实际应用中,常能预先知道参数间的某些先验信息,比如重力场中采用Kaula准则等,可以根据问题的实际情况选择合适的正则化矩阵。分别采用Tikhonov正则化方法(取正则化矩阵为单位矩阵),截断奇异值分解方法和改进的截断奇异值分解方法进行计算。选取其中一次计算的结果展示于图1。可以看出,在一次实验中,3种方法都能减弱病态性的影响,得到与真值相近的估计。Tikhonov正则化方法和TSVD方法都是以参数的二次范数最小为平差准则,未顾及参数间的先验信息,而MTSVD算法由于顾及参数间的先验信息,其结果与真值更为吻合。 表1 不同方法估值的均方根误差比较 图2 重复实验的误差估计情况 测量平差模型的病态性主要是由于观测方程系数矩阵中含有较小的奇异值,这部分较小的奇异值严重放大是观测误差的影响造成的,常用的截断奇异值分解方法是通过删除小奇异值对应的解分量,从而提高解的精度和可靠性。为了充分利用参数中可能存在的可靠先验信息,进一步提高解的精度,本文提出改进的截断奇异值分解方法,主要解决以下问题: 1)将系数矩阵进行奇异值分解,删除小奇异值及对应的奇异向量,得到与系数矩阵近似的秩亏矩阵,证明该秩亏平差模型的最小范数最小二乘解就是常用的截断奇异值解; 2)借鉴Tikhonov正则化算法的思想,对于能预先已知参数间先验信息的病态问题,附加合适的正则化矩阵比单位正则化矩阵能获得更优的解。本文将常规截断奇异值问题中的最小范数条件扩展为参数间线性函数的最小范数条件,提出改进的截断奇异值算法的准则,并得到MP广义逆形式的解; 3)通过对典型病态问题的解算,比较Tikhonov正则化方法、TSVD方法和本文提出的MTSVD算法的性能,从均方根误差的角度,证明新方法优于前两种方法,能有效改善常规TSVD解的精度和可靠性。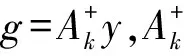
1.3 截断参数的确定
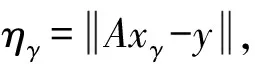
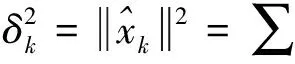
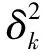
2 修正的截断奇异值分解
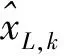
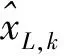
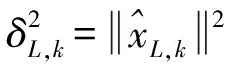
3 算例分析与比较

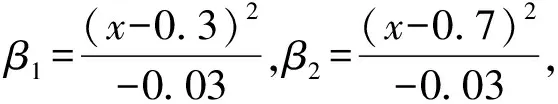

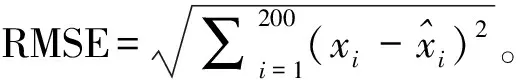
4 结 论
