基于最优邻域局部熵的点云精简算法

林 松，田林亚，毕继鑫，施贵刚，朱依民, 闻 亚

(1. 河海大学 地球科学与工程学院，江苏 南京 211100； 2. 浙江华东测绘与工程安全技术有限公司，浙江 杭州 310014； 3. 安徽建筑大学 土木工程学院，安徽 合肥 230099； 4. 安徽省教育厅 无人机开发及数据应用重点实验室，安徽 马鞍山 243031)

随着三维激光扫描技术的发展，获取高精度高密度的点云数据已经十分普遍，因此扫描得到的点云个数往往是几十万、几百万甚至几亿。在现有的计算机硬件下，庞大的数据量已经成为计算机计算和存储的负担。为了提高数据处理的效率，在保留数据特征且不影响模型重建精度的前提下可以删除部分点云数据，达到点云精简的目的。

国内外研究学者针对点云精简的算法进行了大量的研究，文献[1]提出了包围盒法，建立空间体素格网，采用每个格网内的中心点代替格网内其他点，之后文献[2]提出了均匀格网法，文献[3]提出了非均匀格网精简点云数据，这类基于体素格网的方法原理简单，但是容易丢失细节特征。Chen Y H 等[4]提出了一种基于三角格网的点云精简算法，利用向量加权算法对三角格网片面进行冗余判断，删除冗余三角形以达到精简点云的目的，该方法也未考虑点云特征的问题。近年来，部分学者将曲率值作为判断数据点是否是特征点的依据[5-6]，李金涛等人[7]提出一种基于曲率分级的精简方法，对归一化后的曲率值分级，根据不同等级的点云数据设置不同保留比例，但是基于曲率的点云精简方法容易在平坦区域出现空洞，造成数据缺失。还有随机采样法[8]，其设计一个随机函数，保证每个数据点有相同的概率被删除，同样该方法容易丢失细节特征，且每次运行的结果不一致，精简的精度无法控制。H Benhabiles等[9]将聚类分析与由粗到细策略相结合，提出一种能很好的保留锐利边缘点的方法。陈璋雯等[10]采用模糊熵迭代法精简点云，该方法虽然能有效的保留点云的细节特征，但是大量的曲率计算使得该算法的效率不高。

针对传统的点云精简方法中容易丢失细节特征的问题，文中提出了一种基于最优邻域局部熵的点云精简算法。首先利用主成分分析法(Principal Component Analysis，PCA)[11]计算数据点局部邻域的3个特征值，利用这3个特征值构造维数特征，其次基于维度特征计算局部邻域熵，根据局部熵值确定最优邻域，最后依据特征值之间的关系和局部信息熵剔除平坦区域的数据点完成点云精简。

1 基于特征维数的局部熵

1.1 主成分分析法

主成分分析法是一种设法将原有变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量信息的统计方法，也是数学上用来降维的一种方法。如图1所示，在点云数据处理中常采用PCA算法依据某点的邻域点坐标估计该点的法向量，设P点的邻域点为Pi=[xiyizi]，由式(1)可得到P点的矩阵M为：

(1)

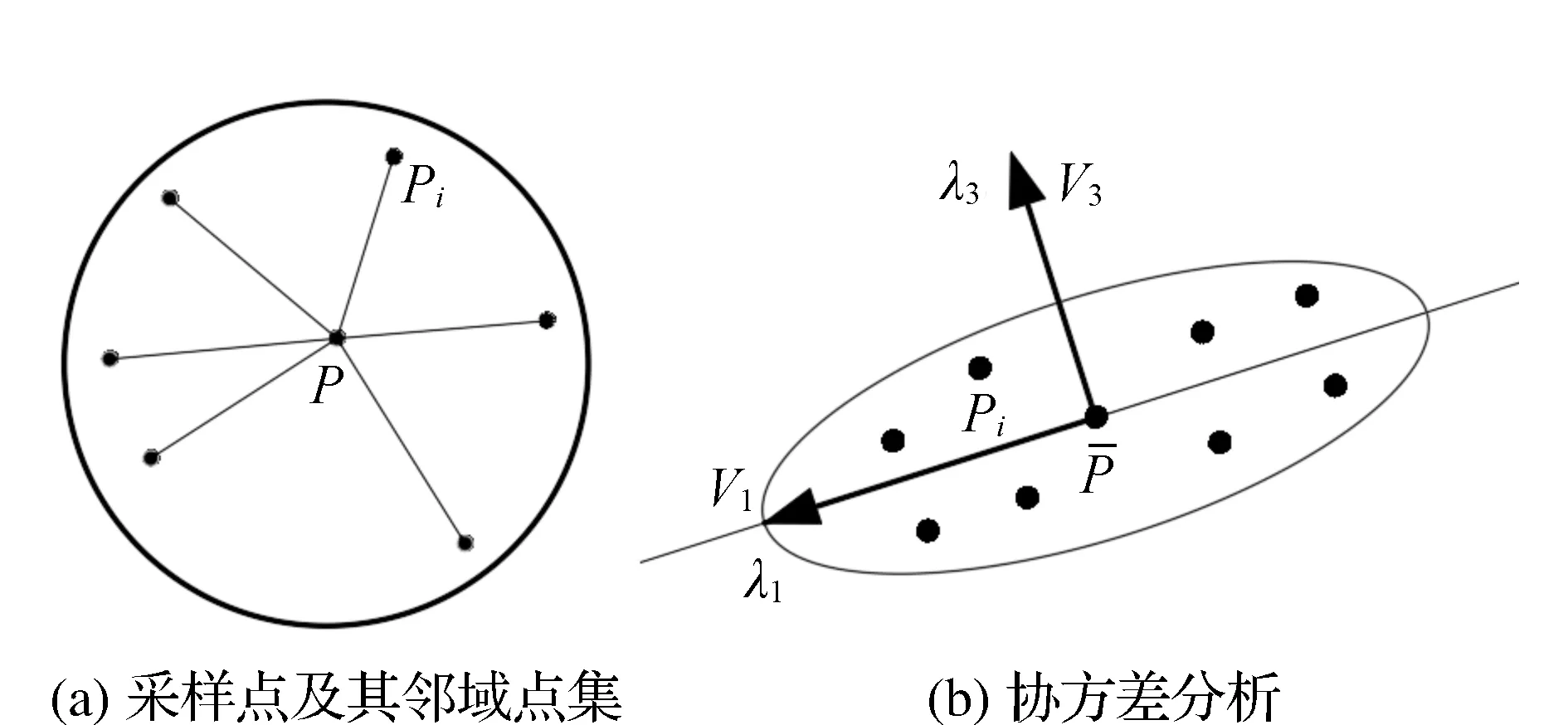
图1 主成分分析法

1.2 局部熵

根据K邻域内的点集进行主成分分析得到点云数据分布的特征值λ1、λ2、λ3(λ1≥λ2≥λ3)，特征值具有以下特性：

1)λ1≥λ2≥λ3时，判定局部邻域为线型。

2)λ1≈λ2≥λ3时，判定局部邻域为平面。

3)λ1≈λ2≈λ3时，判定局部邻域为曲面。

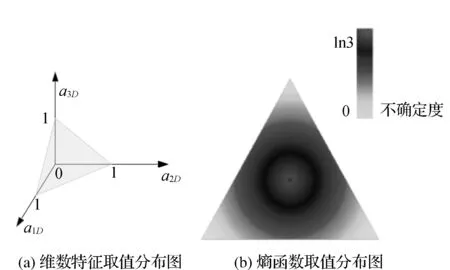
图2 维数特征与熵函数取值分布图

因此可以依式(2)定义维数特征[12]，维数特征描述了局部点云数据的空间分布特征。

(2)

根据香农提出的信息熵理论，可以依据式(3)定义局部熵函数[13]，其中：

Ef=-a1Dln(a1D)-a2Dln(a2d)-a3Dln(a3D).

(3)

则维数特征与熵函数取值分布如图2所示。从局部熵函数可以看出Ef越小，表明其中一种维度特征越明显，说明局部数据点的空间分布特性越相近[14]。

2 基于最优邻域局部熵的点云精简算法

点云精简的主要目的是保留特征点以保留细节特征，现有的精简算法通过某点的曲率来判定该点是否为特征点，通常认为曲率值大的点是特征点，曲率值小的点是非特征点，并删除。曲率值小的点往往是平坦区域的数据点，所以精简的过程主要是过滤局部曲面较为平坦的点集，主要剔除平面或近似平面内的部分点集。根据某点邻域内的点集计算局部熵，若局部熵值小于阈值，且3个特征值关系符合平面特征，则将该点删除，以此完成点云的精简。

2.1 最优邻域的局部熵

不同的邻域大小计算得到的局部熵值不同，为了充分体现局部数据点的空间分布特性，应该找出不同邻域下局部熵值最小的K值，即满足式(4)。因此对于不同的K值，满足Ef最小时所对应的邻域大小称为最优邻域。

K=argmin(Ef).

(4)

因此可以设置最大K值Kmax、最小K值Kmin和步长Δk，计算在区间[Kmin,Kmax]内的局部熵，并找出在该区间内Ef的最小值Efmin，用Efmin作为该点最优邻域的局部熵。

2.2 算法软件实现

基于最优邻域局部熵的点云精简算法的流程如下：

1)首先设置K值的取值范围[Kmin，Kmax]和步长Δk，采用主成分分析法计算Ki邻域下Pi点的3个特征值λ1、λ2、λ3，并依据式(2)、式(3)计算局部熵值，保存每次步长计算得到的局部熵值到链表E。

2)查询链表E中最小熵值对应的K值，将其标记为Pi点的最优邻域，并保存该邻域下的3个特征值到链表T。

3)遍历所有点，每个点的最优邻域局部熵值和最优邻域特征值都保存在链表E和链表T中，剔除链表E中局部熵值小于阈值，且链表T中对应的特征值符合平面特征的点。

3 点云精简算法验证

3.1 模拟数据实验

3.1.1 实验一

采用模拟点云数据A如图3(a)所示进行实验，模拟数据中包含平面点云和曲面点云两种。其中模拟数据为均匀数据，故采用统一的K值，取K=15，不确定度阈值为0.2，分离出曲面点如图3(b)所示，提取的平面点如图3(c)所示，实验表明基于局部熵值和3个特征值能找出平面点云数据。

图3 模拟数据A实验

3.1.2 实验二

采用另一种模拟数据B如图4(a)所示，同样取K=15，不确定度阈值为0.2，分离出曲面点如图4(b)所示，提取的平面点如图4(c)所示，结果表明本文的方法不仅能够剔除平面中的点云，还能剔除部分曲面曲率较小的点。因此对需要精简的对象中每个点云计算其最优邻域的局部熵，若其最优邻域的局部熵值小于给定的阈值，并且3个特征值满足λ1≈λ2≥λ3时，则可将该点删除。

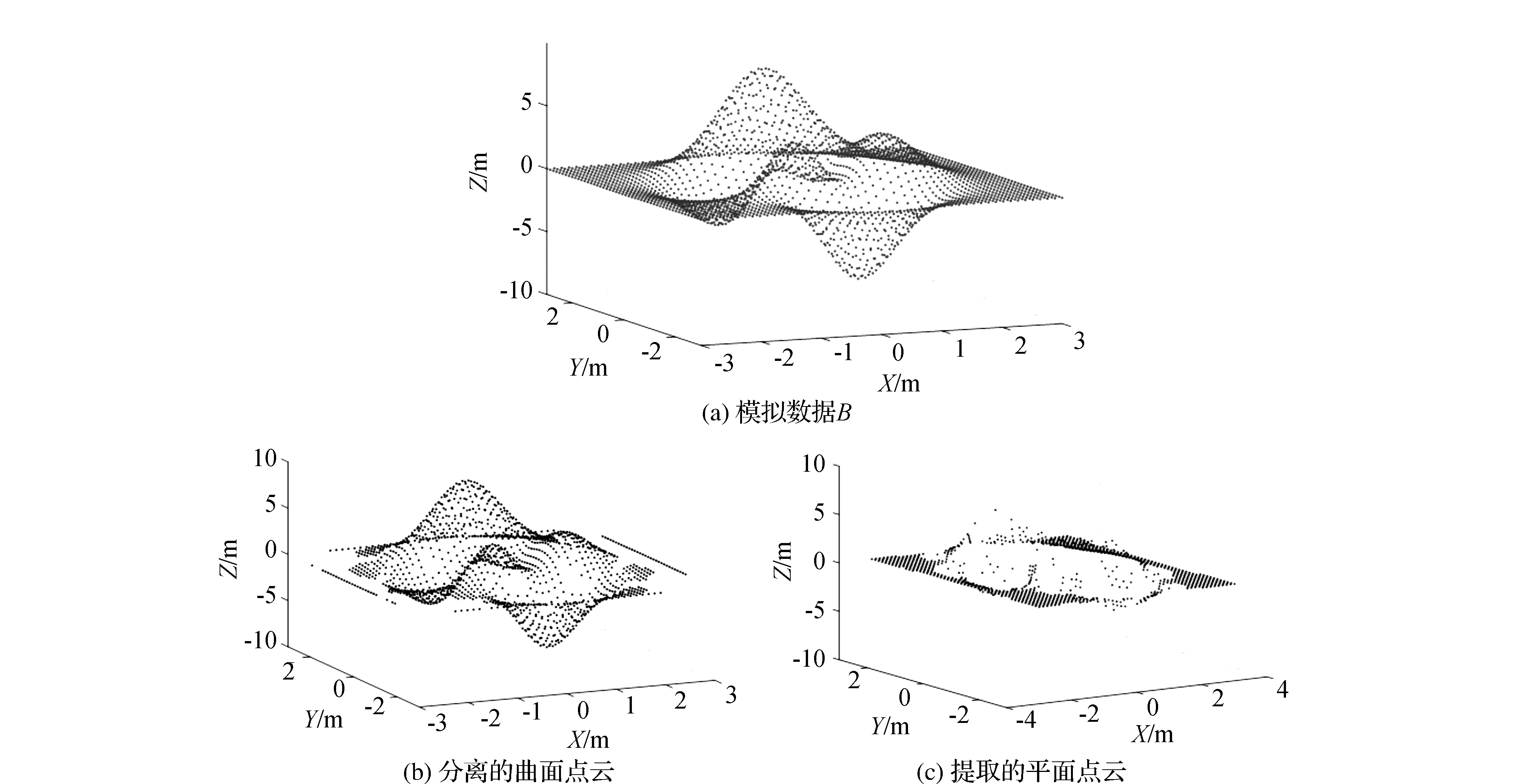
图4 模拟数据B实验

3.2 案例计算与分析

采用Riegl-VZ1000对某公园内龟雕像进行高密度扫描，扫描点云数据如图5所示。本文算法中设置最大K值Kmax=50、最小K值Kmin=10和步长Δk=2，不确定度阈值为0.2，最终压缩率为72.60%。

为了对本文方法进行评价，将本文的方法与传统的基于曲率采样、包围盒法和随机采样3种方法实验结果进行比较。采用基于曲率采样、包围盒法和随机采样3种方法将原始点云数据压缩至72%左右，各方法实验结果如图6和图7所示。

图5 龟雕像原始点云数据

图6 龟雕像点云上半部分不同精简方法比较

图7 龟雕像点云下半部分不同精简方法比较

将龟雕像点云分为3部分如图8所示，1区域细节特征较多，2区域主要是平面区域，3区域包含大量曲面和少量平面区域。不同精简方法在3个区域的精简率如表1所示，4种方法在区域1的精简率相近，说明4种方法在细节较多的区域的精简效果相当。但是在区域2这种平坦的区域，文中的方法和基于曲率采样的方法的精简率明显低于其他两种方法，且文中的方法精简率比基于曲率采样的精简效果更好。对于区域3这样曲面较多的区域，本文的精简效果较差，主要是因为文中的精简算法主要是通过剔除平坦区域的点集达到精简的目的，这也是文中算法的局限性。

文献[15]、文献[16]从表面积和总三角形数两个参数来评价精简的效果，整体的表面积总和以及总三角形个数并不能体现不同方法保留细节特征的效果，因此文中根据雕像的3个区域采用不同精简方法后三角形个数占比来分析不同方法的细节特征保留效果，如表2所示。本文算法在区域2处的三角形个数占比低于其他方法和原始点云的三角形占比，区域1和区域3处的三角形个数占比均高于其他方法和原始点云的三角形占比，说明本文的精简方法在保存细节特征较好的同时剔除了更多平坦区域的数据点。

图8 龟雕像点云分块图

表1 不同精简方法在3个区域的精简率比较

表2 不同方法精简结果比较

4 结束语

随着仪器设备的不断更新，获取海量的点云数据已经非常普遍，海量的点云数据给计算和存储带来了新的挑战，庞大的数据中有大量的冗余信息需要剔除，因此点云的精简对于数据的进一步应用有着十分重要的意义。点云精简是点云数据预处理过程中重要步骤之一，精简的效果直接影响后续数据处理的精度，因此精简过程中需要最大限度的保留细节特征的同时剔除平坦区域的点云。文中提出了一种基于最优邻域局部熵的精简方法，该方法首先通过PCA计算局部区域的3个特征值，并且基于这3个特征值构造特征维度计算局部信息熵，然后根据局部信息熵找出最优邻域，最后根据3个特征值的关系与局部信息熵判断局部形状是否符合平面特征。通过与传统的3种方法实验比较，文中的方法在同样压缩率的情况下能更好的保留细节特征。