薄壁结构多层级并发加筋拓扑优化研究

(1.大连理工大学 工业装备结构分析国家重点实验室，大连 116024；2.大连铭云科技有限公司，大连 116023)

1 引 言

航天装备大量采用网格加筋和周期性点阵等复杂薄壁结构，其重量占装备结构干重的60%以上，轻量化需求十分迫切[1]。尤其面向以空天飞行器为代表的新一代航天装备，其承力薄壁在大型化和精细化设计的发展趋势下，往往还面临高刚度和高抗屈曲等极端承载需求，给轻量化设计造成极大挑战[2]。继续基于传统正置正交或三角形等单一规则加筋形式开展薄壁设计，已难以满足结构的轻质高承载需求，只能通过牺牲结构的力学性能来实现轻量化设计。因此，亟需发展创新结构形式，并建立相应的结构设计方法，充分挖掘结构承载潜力，为新一代航天装备的高性能承力薄壁提供支撑。

多层级结构是一类自然界常见的材料结构形式，其层级化的材料结构特点表现出高刚度、抗屈曲和抗缺陷等各种优异的力学性能[3]。这种通过丰富材料的结构层次来增强其力学性能的方法，为航天承力薄壳的创新结构设计提供了新的设计 思路。

受上述自然材料的启发，本文针对航天装备承力薄壳的高刚度和高抗失稳设计需求，提出了一种薄壁结构的多层级并发加筋拓扑优化方法，可同时给出主层级筋条布局形式和次层级点阵单胞构型，构成层级化的薄壁加筋结构形式。通过不同层级的加筋设计来满足如整体承载和局部抗屈曲等不同层次的承载需求，有效扩展了结构设计空间，发掘利用结构承载潜力，获得高承载的薄壁结构创新构型。

2 国内外现状

早期的薄壁结构加筋设计主要采用均匀周期性网格加筋，如正置正交加筋和等三角加筋等，由于其结构形式相对简单，可以通过全局启发式参数优化和梯度参数优化的两步骤流程获得一组较优异的设计参数[4]，然而，简单的结构形式难以应对复杂且严苛的承载环境，采用复杂的预设结构形式进行层级化结构的参数优化，其增加的参数变量又导致分析和优化迭代计算量呈几何式增长[5]。为解决该问题，代表性工作包括深度学习方法[6]，通过卷积神经网络提取加筋布局特征，从而提升优化迭代效率；近似求解方法[7]，解析地求解特定多层级加筋的失稳系数，从而缩短单次计算时间等。多层级加筋的参数优化研究表明，多层级加筋构型表现出改善结构整体刚度、局部稳定性和可靠性等多方面优点[8]。

然而，参数优化设计方法受制于设计人员预先给出的构型，难以改变加筋构型拓扑，对加筋布局设计域限制较大[9]。相对的，利用拓扑优化方法获取概念设计能极大挖掘结构的承载能力。在薄壁加筋领域，随着拓扑优化理论的发展，学者研究了基结构法[10]、冲压约束[11,12]和B样条参数描述[13]等数值处理技术，成功应用于变密度法、水平集法和刚度扩散法等拓扑优化方法中，突破了早期经典拓扑优化方法低体分比和灰度单元等数值求解问题[14]，实现了利用拓扑优化直接生成加筋特征，并在平面问题和中小规模的三维空间问题上取得了较好的成果。而针对包括航天装备在内的大规模模型问题，上述方法由于高自由度带来的计算效率问题和复杂承载带来的优化收敛问题，难以得到实际工程应用[15]。为解决该问题，有研究基于大型航天薄壁其加筋点阵尺寸远小于整体结构的几何特点，对单胞进行了无限周期性的近似，实现了基于周期性边界条件的等效数值方法，将周期性微结构转化为等效属性，其中代表性的方法有代表体元法[16]和渐进均匀化方法[17]。代表体元法在单胞边界施加单位边界条件，使代表性胞元与某种均匀结构的应变能相等，然后求解该均匀结构的材料属性，力学意义直观；渐进均匀化方法则通过单位特征应变进行渐进摄动展开，具有更严谨的数学基础。利用上述方法，将结构设计转换为材料设计，再根据单胞等效性能与结构形式的关系，就实现了单胞结构的逆均匀化设计，并成功应用于大规模筒壳结构的稳定性设计，有效提升了对薄壁结构的可设计性[18]。

图1 多层级加筋设计

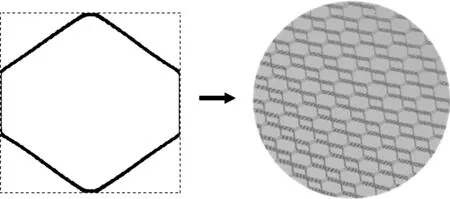
图2 渐进均匀化双尺度加筋单胞设计[18]

homogenization

面向新一代的结构设计需求，为实现进一步丰富结构形式，拓宽结构设计域，有学者提出多尺度设计方法[19]，将整体结构优化称为宏观设计，并在其中增加一组单元内的设计变量以表征材料属性，称为微观设计，实现用一种弱材料替代实心材料，或先获取多种材料属性的整体布局，再通过逆均匀化设计对材料属性进行解释[20]，实现了格栅点阵的构型-布局并发设计[21]。该思路的代表工作是基于多孔各向异性材料法PAMP(Porous Anisotropic Material with Penalty)[22]的涂层-点阵填充优化[23]，利用逆均匀化方法并发获得了平面问题下的涂层点阵设计。面向三维问题的差异化构型设计，有学者提出了实体-格栅并发优化设计[24]，通过一个两步骤的优化进程，实现了典型航天设备的加筋-微桁架布局设计，较传统单层级结构有极大性能提升。研究表明，层级化的设计思想可以提供优越的结构设计潜力，但仍表现出较多限制。现有设计方法或处理平面或小规模问题，而受限于优化计算成本，对高自由度的空间问题适用性差；或以单元尺度表述微结构，导致优化结果约束于单元内，优化构型在微结构的设计变量尺度内变化，层级设计不显著；或使整体布局和微结构分别设计，人为干预性强。

图3 多尺度并发设计方法

基于上述讨论，为实现一种适用于大规模模型的多层级并发加筋设计，需要解决现有研究难以进行主次层级加筋构型清晰表征并优化的问题，突破空间问题下的多层级并发优化技术，进而实现薄壁结构多层级加筋结构优化设计。为此，本文发展了一种薄壁结构多层级并发加筋拓扑优化方法，可同时获得优化的主层级稀疏加筋布局和次层级周期性点阵构型，有效扩展了薄壁结构加筋设计的初始设计域。通过层级化的筋条构型针对性承载不同类型的载荷，有利于提升薄壁结构在复杂载荷下的结构承载效率，为工程薄壁结构的轻质高承载设计提供了更先进的结构优化手段。

3 多层级并发拓扑优化方法

为实现层级化的主层级加筋与次层级点阵的并发优化，需要对两种结构形式的构型进行统一描述，建立两者间的等效刚度传递关系，并在每一次迭代中同步开展两个层级的优化设计。本文提出的多层级并发加筋拓扑优化方法实施流程如图4所示。首先，同时构建主层级筋条和次层级点阵的有限元数值模型，并根据设计需求初始化两个层级的过滤和映射矩阵形式；然后，初始化或更新不同层级的设计变量，对于次层级点阵层次，计算其等效模量，并传递至主层级优化进程中，对于主层级模型，利用刚度和密度插值构建整体有限元分析模型；最后，计算获得响应函数，同步获得响应函数对各层次设计变量的灵敏度，并将上述主次层级分析数据代入优化求解器进行求解。重复上述优化过程直至满足收敛条件，最终获得优化的多层级加筋薄壁结构。

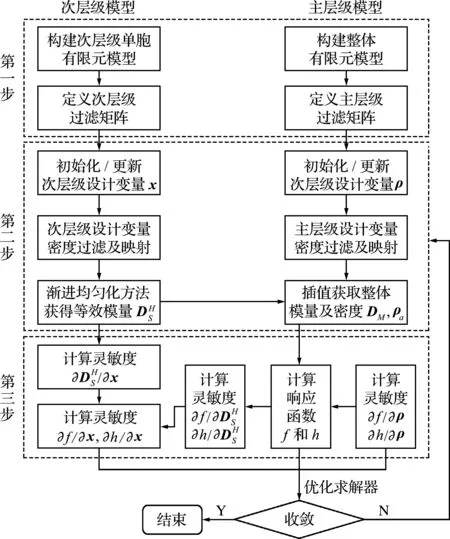
图4 多层级并发拓扑优化流程

上述步骤的关键在于，需要建立主次层级间的等效刚度传递关系，以实现两者的并发优化设计。还需要对周期性次层级结构进行等效表征，避免大规模的次层级分析导致优化迭代耗时无法接受。此外，需要对主次层级设计域施加筋条几何约束，使优化结果呈现为清晰的加筋形式。

3.1 多层级并发拓扑优化模型

多层级并发拓扑优化框架对主层级稀疏加筋和次层级点阵构型进行同时设计并优化迭代。其中，次层级模型通过3.2节所述方法进行构建，主层级模型包含主层级加筋和次层级模型等效获得的等效材料，两者通过插值决定最终的刚度和密度。基于该思想，优化列式表示如下：

s.t.h(ρ,x)≤0

vm(ρ,x)≤0

ρ∈ρa d,x∈xa d

(1)

式中ρ为插值前的主层级有限元模型单元的伪密度，x为次层级点阵有限元模型单元的伪密度或几何模型的控制参数，在3.2节进行具体说明，ρ和x分别为主层级加筋和次层级点阵的设计变量，ρa d和xa d为其可行域。f为目标函数，h为约束函数，vm为体分比约束。DM为主层级加筋和次层级点阵插值获得的等效刚度，插值函数有多种表达形式，本文采用如下的刚度插值函数[25]，

(2)

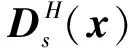
(3)

多层级并发优化的程序实现流程总结如下。

Initialization： 建立多层级有限元分析模型，构建次层级点阵等效模型，初始化模型参数和优化参数，定义过滤矩阵(在3.3节说明)。

(1) 采用渐近均匀化方法求解次层级单胞的等效刚度属性，计算等效刚度对次层级设计变量的导数(在3.2节说明)。

(2) 插值更新整体有限元模型，分析获得目标函数、约束函数值及其对主层级加筋设计变量和次层级点阵等效材料属性的导数。

(3) 通过链式法则分别求解对所有设计变量的敏度。

(4) 求解优化问题，更新设计变量，如果满足收敛准则则结束优化，不满足则返回步骤(1)。

3.2 次层级点阵单胞数值计算模型

为保证多层级并发优化的可行性和设计可用性，采用合理的等效手段将周期性点阵进行简化极为重要。本文采用一种渐进均匀化方法的新求解方法[17]对次层级点阵进行等效，该方法通过将均匀化计算的单位应变场改为等效的位移场，使均匀化计算格式更为简便，简要介绍如下。

首先，采用特征位移表达特征应变，

(4)

(5)

根据单位应变，获得节点反力为

(6)

(7)

式中Ks p为附加周期性边界条件的的单胞总刚度阵。进而获得等效刚度的有限元表达式为

(8)

基于上述方法，就实现了单胞模型的材料等效。如果采用壳单元进行计算，则采用板壳的周期性渐进均匀化方法[17]。本文后续算例均采用实体单元，故不详细说明。

利用等效方法优化单胞构型，根据容许的计算时间、实际工程建模制造可行性等设计需求，本文给出两种单胞结构的设计方法。第一种方法是单胞概念构型拓扑优化设计。该方法直接建立完整的单胞有限元模型，次层级点阵的设计变量为次层级单胞有限元模型单元的伪密度，优化迭代获得拓扑优化生成的单胞构型。等效材料属性对设计变量的敏度为

(9)

第二种方法是典型单胞构型设计，通过构建参数化的单胞几何模型并进行有限元离散，获取等效材料属性，次层级点阵的设计变量为几何模型的控制参数。利用该方法，可以直接使次层级点阵表现为一些工程中常见的构型(如三角形和六边形)。为获得参数化构型等效刚度对设计变量的敏度，如果采用差分法，则需要在每次优化迭代中进行多次计算，计算成本远超出可接受范围。构建数值插值模型能够有效在优化迭代之前一次性完成所有计算，从而在后续迭代步骤中极大幅度缩小该步骤的计算时间[27]。基于上述问题，本文提出一种基于径向基插值函数RBF(Radial Basis Function)[28]的次层级单胞快速等效流程。径向基模型的表达式为

(10)

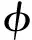
(11)

(12)

式中c为基函数的控制参数。目标函数对变量的敏度可以根据表达式显式地计算。改变模型参数建立多个有限元模型，获得等效刚度中的所有独立变量，就可以构建多个独立变量对参数的径向基函数，并采用拟合精度评判标准对代理模型的精度进行评判，对于样本量较小的模型，常用的评判标准有R2，Adj-R2和均方根误差等[28]。对于部分工程构型，也可以参考其等效刚度解析表达式的研究[29]。为保证单胞的几何特征，在选取周期性结构的单胞形状时需要尽量选择其代表胞元，并且控制单胞尺寸，使其周期阵列与宏观整体结构的设计域相匹配。由于渐进均匀化计算的周期性边界条件施加在单胞上，对单胞单元的数值处理均需要施加周期性条件。

3.3 优化的数值处理方法

变密度法拓扑优化需要通过过滤和映射方法处理棋盘格、灰度单元和网格依赖性等数值问题，薄壁结构的多层级并发拓扑优化方法还需要处理薄壁结构的多层级加筋表征问题。

基于偏微分方程的Helmholtz过滤方法由于不依赖单元临域搜索，在大规模模型上表现出较大优势[29]，并可以通过修改其过滤半径，仅通过单元法向就可以实现大部分结构的加筋特征约束表征[11]。有限元离散的Helmholtz方程可表示为

(13)

(14)

式中N为形函数，c为表示扩散效果的3×3二阶正定张量，

(15)

式中V为单元空间向量的正交基，其中vn为加筋方向，根据数学描述或单元坐标法向量获得，R为过滤半径，rn设置为一个足够大的值(远大于厚度方向)，使过滤后vn方向的密度分布保持水平，在密度过滤时同时实现加筋特征的约束。

对于结构化网格，其单元编号规律简单可循，可以直接设置变量连接以实现加筋特征约束，该线性映射表示为

ρe=Lρd

(16)

式中ρe为次层级单胞的伪密度，ρd为设置了变量连接后优化问题的实际设计变量，L为映射矩阵，该矩阵的构建方法为其第i列的第j行为1，使第j个单元的密度等于第i个单元的密度。

为解决灰度单元的问题，本文采用Heaviside密度映射[30],

(17)

运用上述数值处理方法，任意响应函数对设计变量的灵敏度需要按照链式法则进行修正。

4 算例分析

4.1 四角简支的方板最小化柔顺度优化

以方形板为例，说明本方法在复合载荷条件下的刚度最大化问题。方板板长a=1000 mm，板厚为t=20 mm，主层级加筋筋高为hm=280 mm，次层级点阵高度为hs=130 mm。材料选用铝，弹性模量E=71000 MPa，泊松比ν=0.3。底面的四个顶点沿三个方向固定，使板处于简支状态，施加两个载荷，载荷N1=10000 N为板中心垂直朝向面外的集中力，载荷N2=1000 N为面内对边双向垂直的均布压力。模型采用100×100×12的8节点六面体单元进行离散，其中板厚划分3层单元，为不可设计域，主层级加筋设计域包含8层单元，次层级点阵包含设计域的下4层单元。主层级加筋沿板厚度方向设置变量连接。此外，作为一种合理的工程实践，优化结构设置沿板边垂直平分线对称的变量连接约束，因此，主层级设计变量个数为100×100÷4=2500。结构整体的体积约束设为15%。

图5 四边简支方板模型

本算例优化列式采用方程(1)，其中，目标函数f为结构柔顺度C，其可表示为

(18)

式中DM为主层级加筋和次层级点阵插值获得的等效刚度，由设计变量ρ和x决定，Kk为整体模型单元刚度阵，uk为有限元求解的单元位移。多层级并发拓扑优化的灵敏度推导分为两部分，对主层级加筋设计变量的导数和对次层级点阵设计变量的导数。对于本问题，目标函数对主层级加筋的灵敏度推导与传统拓扑优化方法类似，基于伴随法，可表示为

(19)

式中g′(ρ)为材料插值函数对宏观设计变量的敏度，对于本文选取的插值函数，g′(ρ=pαρ(p -1)-α。在实际处理中，可以首先计算刚度相同单元的应变能，然后再将g′(ρ)作为系数相乘以减少重复计算。

目标函数对次层级点阵等效材料的敏度为

(20)

由于等效刚度系数含21个独立变量，因此对每个单元需要计算21次，为提升计算效率，可以按照同样的方法减少重复计算，并由于单元层级内每个计算之间没有耦合效应，可以采用并行计算技术加快求解效率。获取目标函数对次层级点阵单胞材料系数的灵敏度后，再根据3.2节方法，根据链式法则就可以求得目标函数对微观设计变量的敏度。约束函数h为最大尺寸约束，通过控制半径内的总材料密度，使优化结果呈现为加筋形式，本文采用如下的表达形式[31]，

(21)

式中pn为p范数参数，γ为局部尺寸约束上限。

为完整展示多层级加筋优化方法，并与传统单层级加筋优化方法进行对比，本节共开展三个优化，优化1为传统单层级优化，优化2为基于典型单胞构型设计的多层级并发优化，优化3为单胞概念构型拓扑优化设计的多层级并发优化。在实际处理上，三个优化问题的区别表现为其次层级模型处理上的不同,优化1等价于多层级并发优化中直接令次层级刚度为0。优化2采用正置正交的加筋形式，并利用3.2节所述方法进行等效。为准确描述材料的性能，提供大量不同尺寸的模型进行拟合，由于参数化建模和有限元分析的处理不进入优化迭代循环，因此对整体计算时间没有显著影响。优化3构建次层级单胞网格为100×100×10，并沿厚度方向设置变量连接，因此次层级设计变量为100×100=10000个。

优化结果如图6所示。为更清晰地表示优化结果，通过后处理将次层级点阵构型完整展示在整体模型上。图6的三个优化结果的柔顺度依次为2564.8 J，2363.7 J和2355.3 J。典型构型次层级点阵的多层级并发拓扑优化结果中，主层级加筋与次层级点阵的材料体积比例为VM∶VS=70.9%∶29.1%，拓扑构型次层级点阵的多层级并发拓扑优化结果中，主层级加筋与次层级点阵的材料体积比例为VM∶VS=70.8%∶29.2%。

图6 方板拓扑优化结果

将优化结果总结如图7所示，可以看出，多层级并发优化获得了主层级稀疏加筋和次层级点阵的层级化结构形式，与单层级加筋优化的结构形式区别显著。多层级并发优化刚度较单层级优化刚度有较大提升，两个多层级优化结果(图6(b,c))相对于单层级优化结果(图6(a))，柔顺度分别减小了7.8%和8.2%。该结果表明，通过多层级并发拓扑优化方法，获得的多层级加筋构型承载能力优于单层级加筋构型。

图7 算例1的优化结果对比

为进一步讨论载荷边界对优化结果的影响，修改本算例的载荷大小，分别令N1或N2=0，开展两个新的优化算例。优化结果如图8所示。可以看出，对于仅存在面外集中力N1的载荷工况，最终的优化结果仅包含主层级稀疏加筋，呈现为斜十字形加筋形式，而次层级点阵体积约为0，这一结果与该问题的一般解[9,10,32]相同；而对于只有对边压力N2的载荷工况，其结果仅包含次层级点阵构型，主层级筋条体积约为0，呈现为非均匀的正置正交构型。

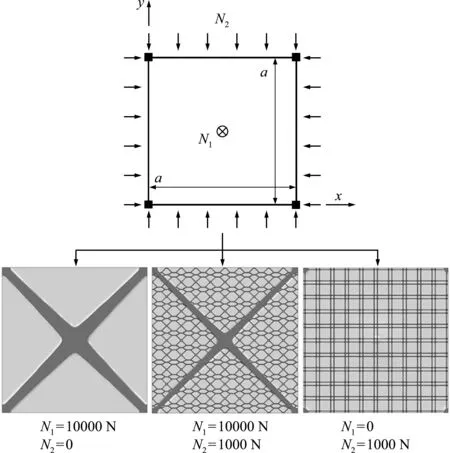
图8 修改承载条件下的多层级优化结果

上述结果表明，尽管多层级加筋结构形式拓展了薄壁结构的初始设计空间，但优化结果的层级化程度与载荷边界具有强相关性，单一载荷边界下的优化结果可能不呈现为多层级构型。具体而言，对于单一的集中载荷边界，优化结果往往呈现为稀疏的主层级加筋形式，且主层级筋条布局接近当前工况下的最优传力路径，从而实现结构整体柔顺度最小化；对于单一的均布载荷边界，优化结果往往呈现为密集的周期性加筋构型，均匀化地增强结构整体，从而抵抗均匀的载荷；对于兼具集中载荷与均布载荷的复杂载荷边界，此时优化结果呈现为多层级加筋构型，通过主层级筋条抵抗集中载荷，通过次层级筋条抵抗均布载荷，从而获得更高承载性能的优化结果。

4.2 稳定性约束下的加筋曲壳最小柔顺度优化

本节以曲壳为例，展示本方法在刚度和稳定性的双重设计需求下的优化效果。加筋曲壳几何模型如图9所示，为一个1/6圆柱壳，其直边长d=500 mm，外径r=250 mm，壳厚t=2 mm，筋高h=8 mm，次层级点阵的高度为主层级筋条的一半，材料选用钢，弹性模量E=210000 MPa，泊松比ν=0.37。曲壳两端约束垂直于曲壳方向的两个自由度，并施加朝向曲壳内的均匀轴压N=800 N。

图9 曲壳模型

模型划分为48384个六面体单元，其中壳厚为3层单元。加筋约束采用3.3节所述的各向异性过滤方法生成加筋，设置加筋方向过滤半径rn=1500。体分比约束为30%，主层级设计变量为48384个。优化目标为在保证结构一阶线性临界失稳系数大于1的前提下最小化结构柔顺度。对于该问题，注意需要对次层级等效材料的主方向进行设置，弹性矩阵的转换矩阵表达式为

(22)

本算例的优化列式采用方程(1)，其中，目标函数f为结构柔顺度C，其表达式和敏度推导与4.1节相同。约束函数h为结构一阶线性临界失稳载荷，其计算及其敏度计算推导如下。一般而言，求解结构失稳临界承载力的特征值问题是求解其逆特征值为

(23)

式中Kσ M为初应力矩阵(几何刚度阵)，KM为结构刚度阵，两者均通过主层级加筋和次层级点阵刚度插值并组合。单元的初应力矩阵表示为

(24)

式中G为排序后的形函数微分项，S为结构应力矩阵，其表示为

(25)

(26)

KM的相关计算见4.1节。Kσ M对任意设计变量的导数为

(27)

为避免计算∂u/∂x，利用伴随法计算如下,

(28)

式中伴随向量v根据以下伴随方程求解，

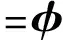
(29)

式中Kσ M的偏导数计算只需要计算其中结构应力矩阵S的偏导数，关于其分项s的计算表达式为

(30)

式中I为单位矩阵。对次层级单胞设计变量的敏度同样利用链式法则计算获得。

构建与4.1节相似的三个优化问题，其中，优化2选用正三角形单胞，优化3构建单胞模型划分为80×80×20个单元，沿厚度方向设置变量连接，并设置对称约束，变量数为80×80÷4=1600。

优化结果如图10所示，图10的三个优化结果的一阶失稳系数依次为1.52，1.28和1.36，满足稳定性约束，三者的柔顺度依次为506.88 kJ，432.19 kJ和372.08 kJ。典型构型次层级点阵的多层级并发优化结果中，主层级加筋与次层级点阵的材料体积比例为VM∶VS=60.1%∶39.9%，拓扑构型次层级点阵的多层级并发优化结果中，主层级加筋与次层级点阵的材料体积比例为VM∶VS=66.5%∶33.5%。将优化结果总结如图11所示，并展示了三个优化结构的一阶失稳模态。结果显示，两个多层级优化结果(图10(b，c))相对于单层级优化结果(图10(a))，柔顺度分别减小了14.7%和26.6%，多层级并发优化的刚度相对于单层级优化有显著提升。

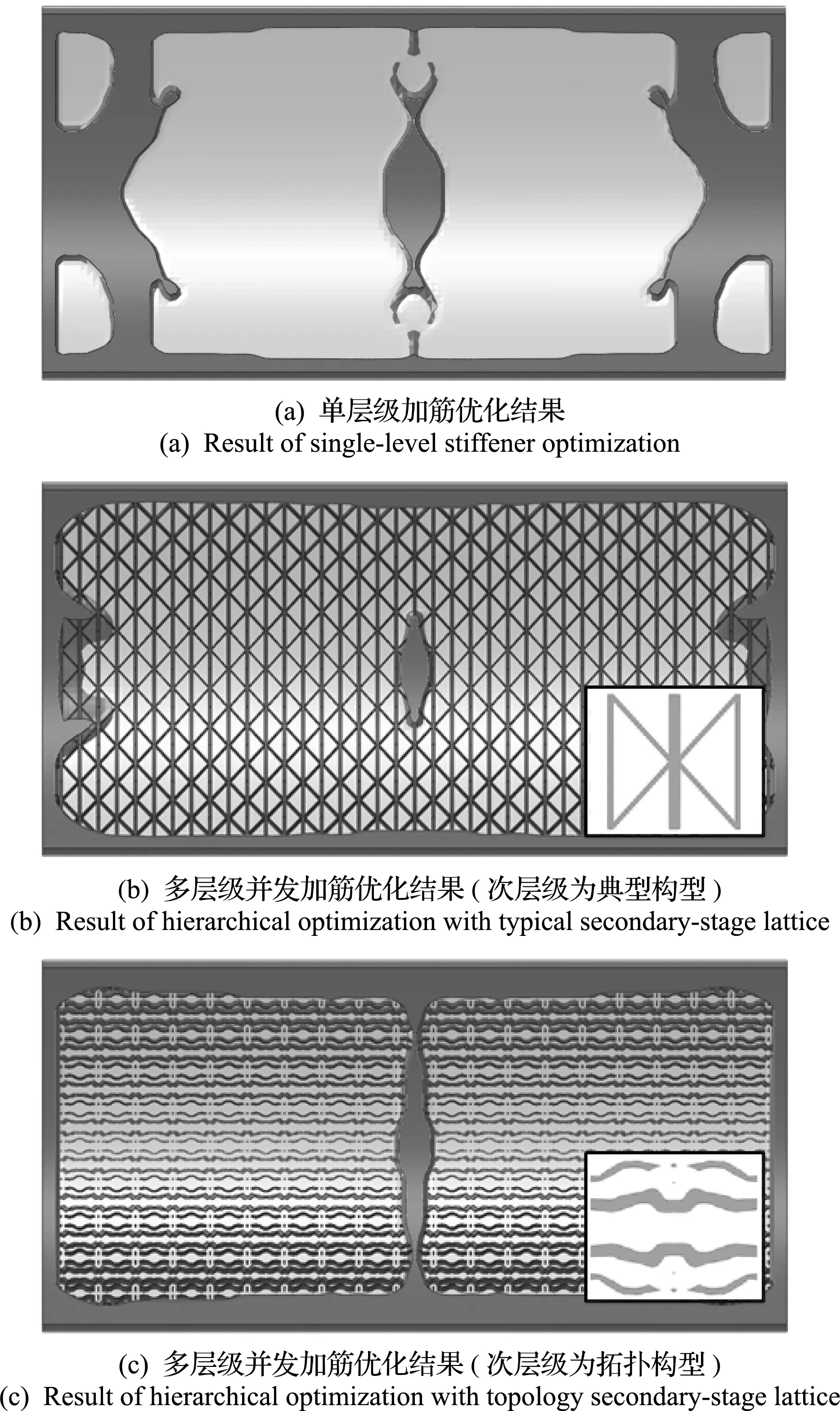
图10 曲壳优化结果

图11 算例2的优化结果对比

本节算例的多层级并发优化构型同样呈现出与单层级加筋优化的明显区别。在双重设计目标的复杂约束下，单层级加筋结构为提升结构抗失稳能力，将部分材料布置于非直接传力路径，导致结构整体刚度下降，而多层级加筋构型通过主次层级筋条共同作用，在保证结构整体承载能力的同时，同步增强薄壳整体和局部抗弯刚度，改变结构失稳模态，提升结构抗屈曲能力。其次，上述算例中，在相同的屈曲约束下，拓扑点阵优化构型的结构承载力明显优于预设的正三角点阵优化构型，前者的柔顺度降低程度是后者的1.8倍。这说明，相比传统单层级加筋和典型次层级点阵的多层级加筋设计，主层级筋条布局和次层级点阵构型的共同设计可给出更优的兼具刚度和抗屈曲承载能力的薄壁结构设计。

5 结 论

本文提出了一种薄壁结构的多层级并发加筋设计方法，在一次拓扑优化求解中同时生成主层级稀疏加筋和次层级密集点阵构型，扩展了结构优化设计空间，获得创新结构形式，利用主次层级的筋条结构针对性地抵抗复杂载荷边界，有效提升了材料利用率。优化算例表明，多层级并发加筋可以优化两层级加筋的体积比例及两层级加筋的拓扑布局，优化结构承载效率，在复杂边界环境及设计指标下，主次层级加筋可以协同作用，有效提升结构承载能力。本方法提供的优化构型工程实用性强，能够有效应用于航天装备的薄壁结构优化，也可以延拓至常见薄壁结构主承力结构，从而有效提升装备薄壁结构的承载效率。

参考文献(References):

[1] 王 博，郝 鹏，田 阔.加筋薄壳结构分析与优化设计研究进展[J].计算力学学报,2019,36(1):1-12.(WANG Bo,HAO Peng,TIAN Kuo.Recent advances in structural analysis and optimization of stiffened shells [J].ChineseJournalofComputationalMe-chanics,2019,36(1):1-12.(in Chinese))

[2] 全栋梁,时光辉,关成启,等.结构优化技术在高速飞行器上的应用与面临的挑战[J]:力学与实践,2019,41(4):373-381,415:(QUAN Dong-liang,SHI Guang-hui,GUAN Cheng-qi,et al.Applications and challenges of structural optimization in high-speed aerocraft [J].MechanicsinEngineering,2019,41(4):373-381,415.(in Chinese))

[3] Fratzl P,Weinkamer R.Nature’s hierarchical materials[J].ProgressinMaterialsScience,2007,52(8):1263-1334.

[4] Bagheri M,Jafari A A,Sadeghifar M.A genetic algorithm optimization of ring-stiffened cylindrical shells for axial and radial buckling loads[J].ArchiveofAppliedMechanics,2011,81(11):1639-1649.

[5] 邓亚权.基于代理模型的结构疲劳寿命优化方法、软件及应用[D].南京航空航天大学,2010.(DENG Ya-quan.Method,Software and Application of Structural Fatigue Life Optimization Based on Metamodels[D].Nanjing University of Aeronautics and Astronautics,2010.(in Chinese))

[6] Hao P,Liu D C,Zhang K P,et al.Intelligent layout design of curvilinearly stiffened panels via deep lear-ning-based method[J].Materials&Design,2021,197:109180.

[7] 徐元铭，李松泽.整体次加筋壁板屈曲载荷近似计算方法[J].北京航空航天大学学报,2015,41(3):369-374.(XU Yuan-ming,LI Song-ze.Approximate calculation method of buckling load on integral sub-stiffened panel[J].JournalofBeijingUniversityofAeronauticsandAstronautics,2015,41(3):369-374.(in Chinese))

[8] Wang B,Tian K,Zhou C H,et al.Grid-pattern optimization framework of novel hierarchical stiffened shells allowing for imperfection sensitivity[J].AerospaceScienceandTechnology,2017,62:114-121.

[9] 钟焕杰.薄壁加筋结构的拓扑优化方法研究[D].南京航空航天大学,2015.(ZHONG Huan-jie.Research on Topology Optimization of Stiffened Plates[D].Nanjing University of Aeronautics and Astronautics,2015.(in Chinese))

[10] 董小虎，丁晓红.基于自适应成长法的周期性加筋结构拓扑优化设计方法[J].中国机械工程,2018,29(17):2045-2051.(DONG Xiao -hu,DING Xiao -hong.Topology optimum design method for periodic stiffe -ner structures based on adaptive growth method[J].ChinaMechanicalEngineering,2018,29(17):2045-2051.(in Chinese))

[11] Wang B,Zhou Y,Tian K,et al.Novel implementation of extrusion constraint in topology optimization by Helmholtz-type anisotropic filter[J].StructuralandMultidisciplinaryOptimization,2020,62(4):2091-2100.

[12] 张卫红，章胜冬，高 彤.薄壁结构的加筋布局优化设计[J].航空学报,2009,30(11):2126-2131.(ZHANG Wei-hong,ZHANG Sheng-dong,GAO Tong.Stiffener layout optimization of thin walled structures[J].ActaAeronauticaetAstronauticaSinica,2009,30(11):2126-2131.(in Chinese))

[13] Feng S Q,Zhang W H,Meng L,et al.Stiffener layout optimization of shell structures with B -spline parame -terization method[J].StructuralandMultidisciplinaryOptimization,2021,63(6):2637-2651.

[14] Olhoff N,Bendsøe M P,Rasmussen J.On CAD -integrated structural topology and design optimization[J].ComputerMethodsinAppliedMechanicsandEngineering,1991,89(1-3):259-279.

[15] Wagner H N R,Hühne C,Rohwer K,et al.Stimulating the realistic worst case buckling scenario of axially compressed unstiffened cylindrical composite shells[J].CompositeStructures,2017,160:1095-1104.

[16] Xia Z H,Zhang Y F,Ellyin F.A unified periodical boundary conditions for representative volume elements of composites and applications[J].InternationalJournalofSolidsandStructures,2003,40(8):1907-1921.

[17] 蔡园武.周期性板结构的渐近均匀化方法及微结构优化[D].大连理工大学,2014.(CAI Yuan-wu.Asymp -totic Homogenization of Periodic Plate and Micro -Structural Optimization[D].Dalian University of Technology,2014.(in Chinese))

[18] Zhou Y,Tian K,Xu S L,et al.Two -scale buckling topology optimization for grid-stiffened cylindrical shells[J].Thin-WalledStructures,2020,151:106725.

[19] Wu J,Sigmund O,Groen J P.Topology optimization of multi-scale structures:a review[J].StructuralandMultidisciplinaryOptimization,2021,63(3):1455-1480.

[20] Rodrigues H,Guedes J M,Bendsoe M P.Hierarchical optimization of material and structure[J].StructuralandMultidisciplinaryOptimization，2002,24(1):1-10.

[21] 易斯男.基于均匀化的周期性梁板结构降阶及拓扑优化[D].大连理工大学,2015.(YI Si-nan.Model Reduction and Topology Optimization of Periodic Beam and Plate Structure Based on Homogenization[D].Dalian University of Technology,2015.(in Chinese))

[22] 刘 岭，阎 军，程耿东.考虑均一微结构的结构/材料两级协同优化[J].计算力学学报，2008,25(1):29-34.(LIU Ling,YAN Jun,CHENG Geng-dong.Structure -material concurrent optimization considering uniform material microstructure[J].ChineseJournalofComputationalMechanics,2008,25(1):29-34.(in Chinese))

[23] Wadbro E,Niu B.Multiscale design for additive ma-nufactured structures with solid coating and periodic infill pattern[J].ComputerMethodsinAppliedMe-chanicsandEngineering，2019,357:112605.

[24] Wang C,Zhu J H,Wu M Q,et al.Multi-scale design and optimization for solid-lattice hybrid structures and their application to aerospace vehicle components[J].ChineseJournalofAeronautics，2021,34(5):386-398.

[25] Sigmund O.Design of multiphysics actuators using topology optimization.Part II:Two -material structures[J].ComputerMethodsinAppliedMechanicsandEngineering，2001,190(49-50):6605-6627.

[26] Zhu J H,Zhang W H,Beckers P.Integrated layout design of multi-component system[J].InternationalJournalforNumericalMethodsinEngineering，2009,78(6):631-651.

[27] Wang C,Gu X J,Zhu J H,et al.Concurrent design of hierarchical structures with three -dimensional para-meterized lattice microstructures for additive manufacturing[J].StructuralandMultidisciplinaryOptimization，2020,61(3):869-894.

[28] 艾依斯，张爱莲，吴义忠.一种改进的RBF全局优化方法[J].计算机工程与应用，2012,48(15):43-48.(AI Yi-si,ZHANG Ai-lian,WU Yi-zhong.Improved global optimization method using radial basis functions[J].ComputerEngineeringandApplications,2012,48(15):43-48.(in Chinese))

[29] Lazarov B S,Sigmund O.Filters in topology optimization based on Helmholtz-type differential equations[J].InternationalJournalforNumericalMethodsinEngineering，2011,86(6):765-781.

[30] Guest J K,Prévost J H,Belytschko T.Achieving minimum length scale in topology optimization using nodal design variables and projection functions[J].InternationalJournalforNumericalMethodsinEngineering，2004,61(2):238-254.

[31] Guest J K.Imposing maximum length scale in topology optimization[J].StructuralandMultidisciplinaryOptimization，2009,37(5):463-473.

[32] 崔荣华.基于拓扑优化框架的薄板加强筋布局优化[D].大连理工大学,2019.(CUI Rong-hua.Layout Optimization of Stiffeners Based on Topology Optimization Framework[D].Dalian University of Techno -logy,2019.(in Chinese))