不平衡数据加权边界点集成欠采样方法
2021-09-02何云斌
何云斌,冷 欣,万 静
(哈尔滨理工大学 计算机科学与技术学院,黑龙江 哈尔滨 150000)
近年来,随着人工智能和大数据的发展,不平衡数据已经广泛出现在人们的现实生活中,如医学领域[1]、信用卡欺诈检测[2]、文本分类[3-4]、垃圾邮件的检测[5]以及故障检测[6]等领域。在以上领域少数类数据集往往发挥更重要的作用。但是人们一直忽略少数类信息所特有的价值,过多地关注多数类信息,而且被错分的样本往往是少数类数据,因此提高少数类的识别率是非常有必要的。
文献[7]提出基于聚类的欠采样方法,将多数类中的簇数设置为等于少数类中的数据点个数,提出两种策略进行聚类:第1种是使用聚类中心来表示多数类,第2种是使用每个聚类中心的最近邻来表示多数类。研究了5到10个聚类中心的添加或删除对多数类数据性能的影响。文献[8]提出一种基于样本权重的不平衡数据欠抽样方法(KAcBag),通过bagging成员分类器得到若干决策树子分类器,最后进行加权投票生成预测模型。该算法所选数据具有较强的代表性,可以有效提高少数类的分类性能,但是在聚类时需要通过实验来获得聚类次数、类簇的个数以及簇减少的步长等参数,耗费时间较多。文献[9]提出一种基于距离的支持向量机加权欠采样方法,是一种改进的WU-支持向量机算法,将大多数样本划分为一些子区域(SRS),并根据它们到超平面的欧几里得距离分配不同的权重。文献[10]通过改进惩罚函数,有效处理含有噪声点的非平衡数据集,并采用网格搜索算法来确定各个支持向量机模型中参数的优化取值。
在欠采样方法中,现有的对多数类数据进行处理的方法大多都是忽略边界点的计算,但是边界点中往往含有有用的信息,所以对边界点进行删除对不平衡数据的预处理是有影响的。为了有效解决多数类样本集中含有的边界点问题,笔者通过研究多数类样本的分布情况,提出一种基于边界点加权的不平衡数据集成欠采样方法。首先,对多数类数据进行聚类;其次,对边界点进行加权,约简数据集;最后,使用AdaBoost成员分类器对平衡数据集进行训练并通过加权投票生成预测模型。
1 基于聚类的欠采样方法
笔者提出的基于聚类的集成欠采样方法主要分为4部分,即对多数类数据进行聚类、边界点加权、删除低密度数据簇和数据加权集成分类。
1.1 多数类数据集的聚类
记多数类数据集N={d1,d2,…,dn},少数类数据集M={s1,s2,…,sm},边界点集S={b1,b2,…,bt}。首先以少数类数据集中的样本数作为初始聚类中心个数,对多数类数据采用k均值聚类方法进行聚类,形成初始的聚类簇。
不平衡数据的聚类过程,如图1所示。
从图1(a)可以看出,不平衡数据集中含有多数类数据和少数类数据。图1(b)中含有的少数类数据个数是7个,运用k均值聚类[11]对多数类数据进行聚类,形成的初始聚类中心的个数为7个,所得到的初始聚类簇为7个。
基于以上的理论分析,算法的主要过程及计算步骤为:首先以少数类数据集中的个数m作为多数类数据集初始聚类中心的个数,计算每个样本到所有聚类中心的欧氏距离,每个样本di选择最近的聚类中心oj,并将该样本加入到与其最近的聚类中心所在的聚类簇Wj中,把所有样本放在不同的集合后,得出一共有m个集合。然后重新计算每个集合中所有对象的平均值,作为新的簇中心。计算方法是计算该簇中所有对象的平均值,也就是分别对所有对象的各个维度的值求平均值,从而得到簇的中心点。例如:一个簇包括以下3个数据对象{(1,3,3),(2,6,4),(3,3,5)},则这个簇的中心点就是((1+2+3)/3,(3+6+3)/3,(3+4+5)/3)=(2,4,4)。不断重复上述过程,直到准则函数收敛,也就是簇中心不再发生明显的变化。
算法1多数类数据集聚类算法(Clustering_MCD(N,M))。
输入:多数类数据集N={d1,d2,…,dn},少数类数据集M={s1,s2,…,sm}。
输出:聚类结果W={W1,W2,…,Wm}。
①k←count num(M);/*少数类数据集的样本个数*/
② 在数据集N的样本中,随机选择m个样本作为初始聚类中心,m个初始聚类中心记为O={o1,o2,…,om},并放入相应的聚类结果Wj中;
③ fori=1 tondo
④ forj=1 tomdo
⑤ calculate dist(di,oj); /*计算每个样本到所有聚类中心的欧氏距离*/
⑥ end for;
⑦ select_center(oj);/*每个样本dj选择最近的聚类中心oj*/
⑧ join_center(Wj);/*加入该聚类中心所在的聚类簇Wj中*/
⑨ end for;
⑩ forj=1 tomdo
1.2 边界点加权
在图1所得到的初始聚类簇中,将聚类边界点提取出来,然后对提取出的边界点进行加权,形成新的多数类样本集。
1.2.1 提取边界点
薛丽香等[12]提出的算法通过引入变异系数刻画数据集的分布特征,进而提取出聚类边界点。该方法可以在含有噪声的数据集上将边界点与噪声点以及孤立点分离开,有效检测出聚类边界点。通过引入变异系数将边界点输出。主要利用密度的标准差与密度的平均值来刻画数据的分布特征。如果一个数据对象的变异系数越大,那么就说明该点附近点的密度的分布相对离散,密度变化较大,数据分布不均匀,即该点附近既有高密度的区域,也有低密度的区域,该点成为边界点的可能性就越大。
定义1数据对象的边界因子。给定一个数据对象pi和pi的局部密度与整个数据集中所有对象局部密度的平均值的比值作为数据对象pi的边界因子,记为B。计算公式如下:
(1)
如果一个边界点的局部密度越大,那么它的边界因子也越大;相反,如果一个边界点的局部密度越小,那么它的边界因子就越小。
给定数据集D={p1,p2,…,pn},pi∈D,1≤i≤n,其中在数据集D中包含n个数据对象,在这里选取任意一个数据对象pi作为代表点进行相关运算。假设pi和pj是数据集D中的对象,对象pi和pj之间的距离记作d(pi,pj)。
定义2数据对象pi的k距离[13]。对任意的正整数k和数据集D,数据对象pi的k距离记作k_dist(pi),并定义其为数据对象pi与数据对象o∈D之间的距离d(pi,o)。且满足:
(1) 至少有k个数据对象qi∈D-{pi},使得d(pi,qi)≤d(pi,o),i=1,2,…,k;
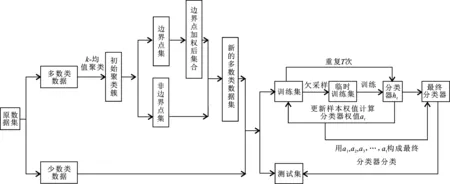
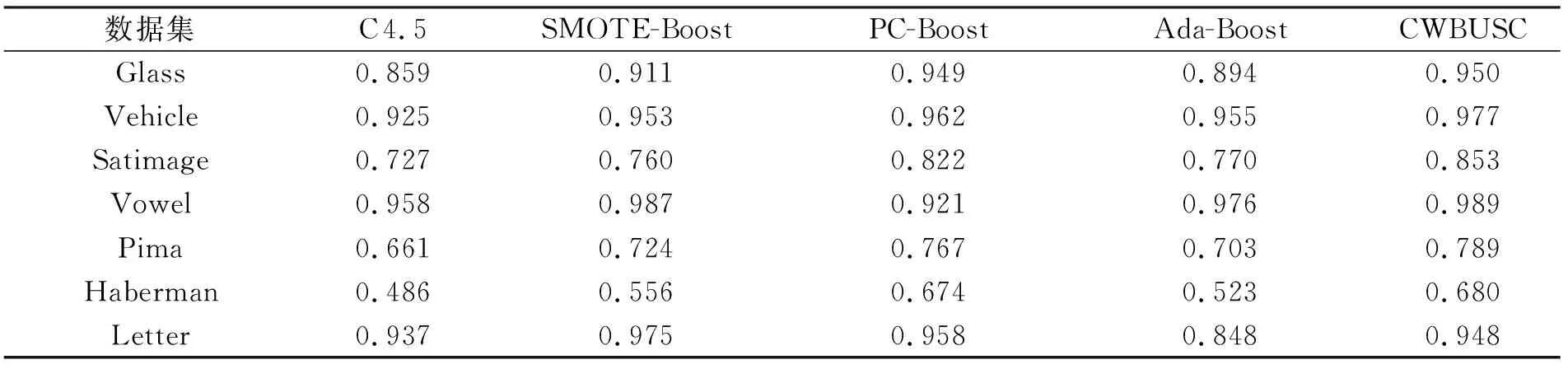
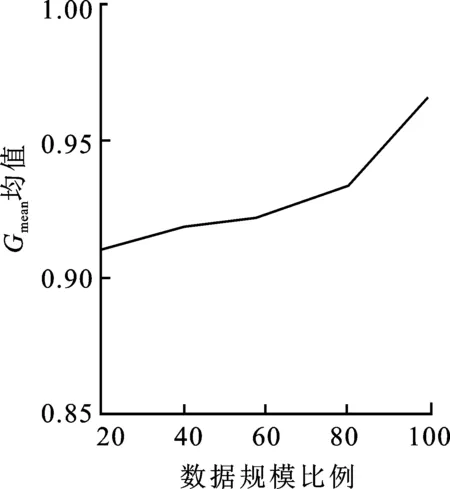
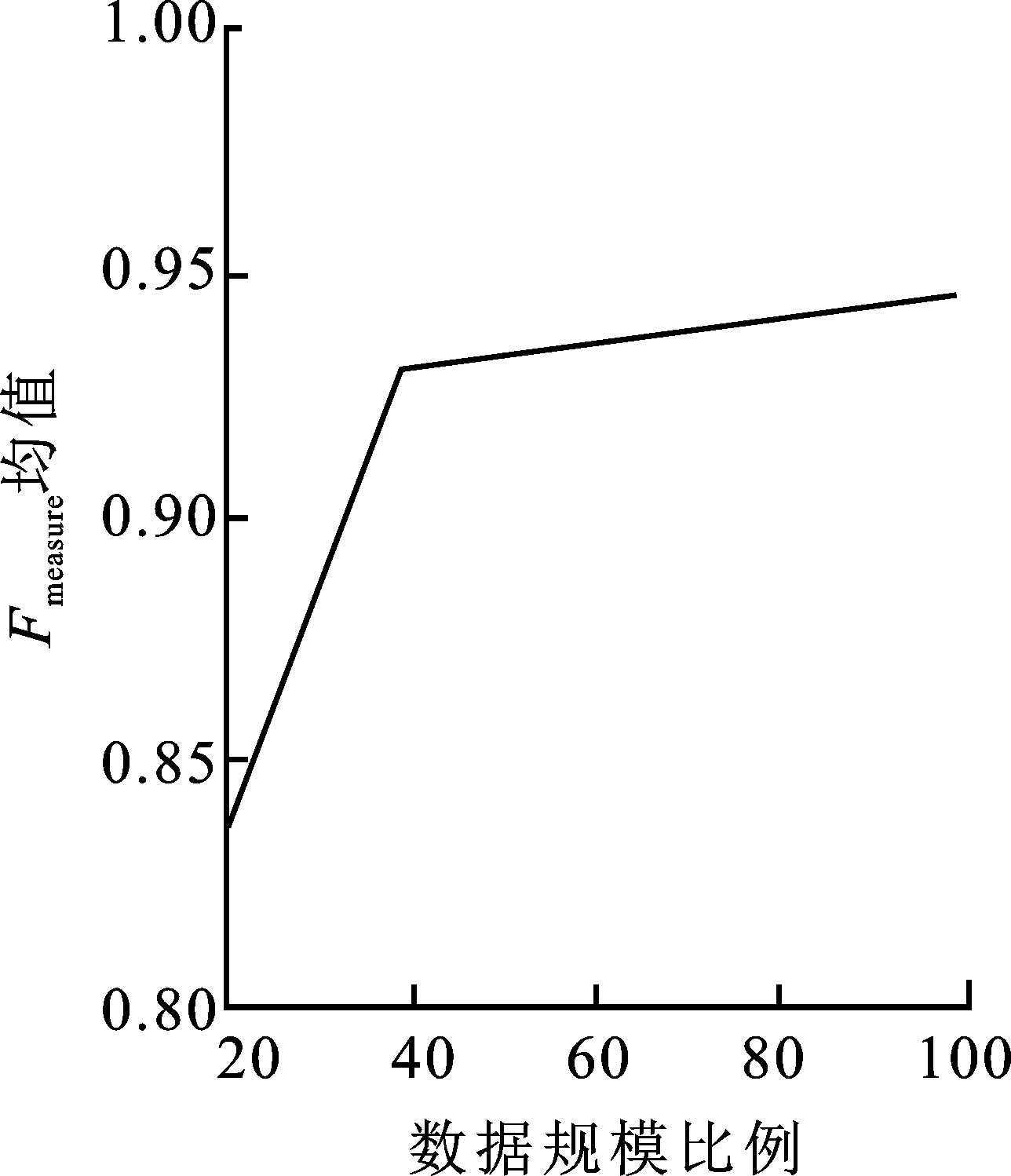
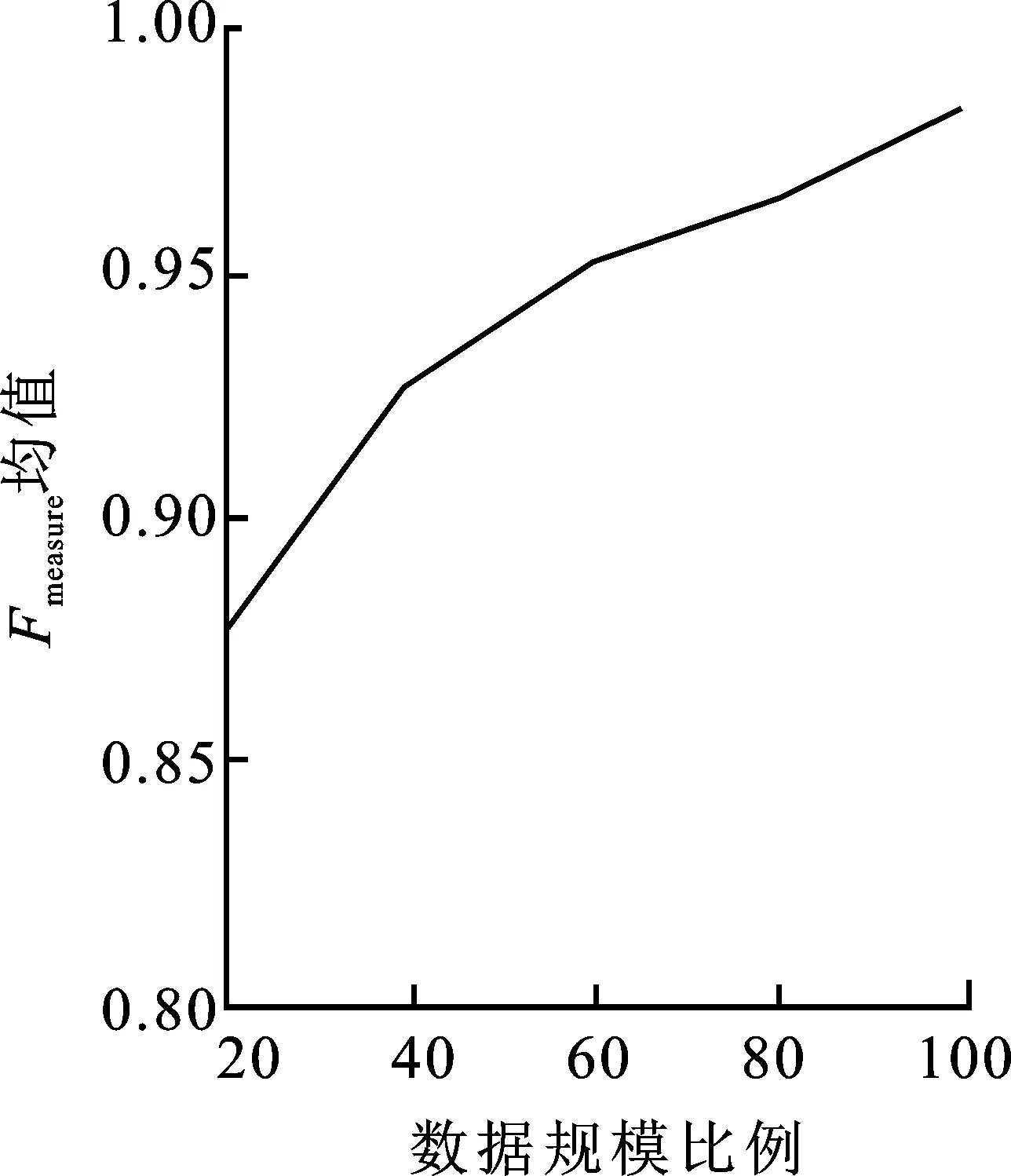
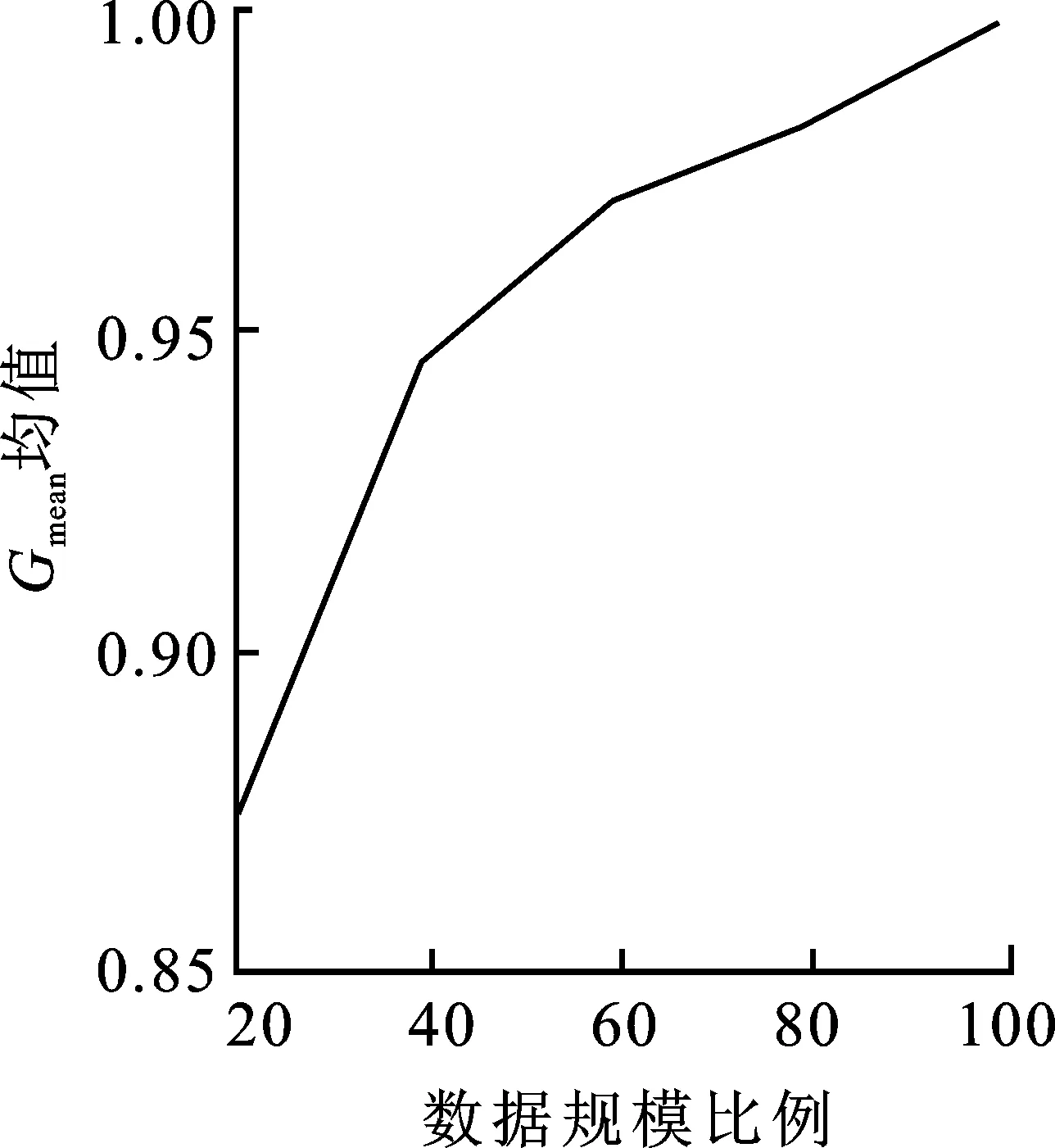
(2) 至多有k-1个数据对象qi∈D-{pi},使得d(p,qi) 定义3数据对象pi的局部密度[12],定义为数据对象pi与其k距离邻居距离和的平均值的倒数: (2) 其中,d(pi,qi)是数据对象pi与其k距离邻居之间的距离。 (3) 1.2.2 边界点加权算法 本节提出的边界点加权算法首先是引用文献[14]识别边界点的过程,对这一过程中所得到的边界点集进行操作;其次给出权重大小,让边界点集上的每一个数据点和权重相乘,得到加权后的边界点集。因此,使得边界点中具有价值信息的点不被删除,提高了分类结果的准确性。 定义4边界点[14]。根据每个对象的反向k近邻值按从小到大的顺序排列整个数据集,并把前n个对象作为边界点。 定义5权重[15]。对任意的数据集D,数据点pi的权重ωpi定义为 (4) 定义6加权边界点。数据集D中边界点pi的加权边界点ω(pi),定义为 ω(pi)=B(pi)ωpi, (5) 其中,ω(pi)记录的是每个边界点pi与权重ω的乘积。由加权边界点ω(pi)组成的集合叫作加权边界点集合。根据边界点和权重的定义可得,靠近非边界点集的边界点会具有较高的权重,而这类点是具有价值信息的边界点的概率更大。因此,结合边界点和权重,使得算法在更好地保留边界点的同时,能够尽可能地提高发现边界点中有价值的点的概率,再次提高分类的准确性。 算法2边界点加权算法(BDP_W(N,M))。 输入:多数类数据集N={d1,d2,…,dn},少数类数据集M={s1,s2,…,sm}。 输出:加权边界点集合S′,加权后的多数类数据集N′。 ①S′←∅;/*初始化加权边界点为空集*/ ②W←Clustering_MCD(M,N);/*调用算法1*/ ③S←BAND(W);/*调用BAND算法生成边界点集*/ ④ fori=1 totdo ⑤ calculateB(pi);/*公式(1)*/ ⑥ calculateωpi;/*公式(4)*/ ⑦ calculateω(pi);/*公式(5)*/ ⑧ end for; ⑨S′←ω(pi);/*形成加权边界点集合*/ ⑩N′←S′∪N-S;/*形成加权后的多数类样本集*/ 给定样本集N′=C1∪C2∪…∪Cn,Ci(i=1,2,…,n)代表一个簇,Ci={X1i,X2i,…,Xmi},其中Xki(k=1,2,…,m)是Ci中的一个样本。 定义7簇密度。一个簇Ci的簇密度为样本集N′中簇Ci中数据对象的个数,记为T(Ci)。 定义8平均密度。样本集N′的平均密度计算公式为 (6) 基于以上理论分析,算法的主要过程和计算步骤如下。 算法3约简数据集算法(RE_DS(N,M))。 输入:多数类数据集N={d1,d2,…,dn},少数类数据集M={s1,s2,…,sm}。 输出:约简后的多数类数据集和少数类数据集结合形成平衡的数据集Nall。 ①N′,S′←BDP_W(N,M);/*调用算法2*/ ② fori=1 tondo ③ countT(Ci);/*计算每个类簇的数据对象的个数*/ ④ end for ⑤ Quick_Sort(T(Ci));/*降序排序*/ ⑧Nnew←Ci;/*Ci为高密度类簇*/ ⑨ else ⑩ deleteCi;/*删除Ci*/ 基于聚类的加权边界点的欠采样过程中利用聚类方法在保留多数类数据特征的基础上使得不平衡数据集变成平衡数据集,集成分类则是基于集成学习的方法在已经均衡的数据集上进行分类学习,最终输出强分类器的过程。分类模型如图2所示。 图2 基于欠采样的不平衡数据集成分类模型 不平衡数据集经过算法1、算法2以及算法3处理后,得到平衡数据集,对平衡数据集使用AdaBoost算法进行训练,得出分类模型。 经过算法1~3后形成平衡的数据集,在数据训练阶段的每次迭代过程中权重会不断进行更新。将D1(i)初始化,得 (7) 其中,n表示平衡数据集中样本的个数。经过t次迭代训练结束时,得到子分类器ht(x),子分类器ht(x)形成后的权值更新记为Dt+1(i)[16],则有 (8) 其中,Nall为t次迭代后的训练样本集。Zt[16]为归一化常量,可表示为 (9) 第t次迭代所得子分类器的训练误差记为et[16],可表示为 (10) 由式(10)训练误差et,得到子分类器参数记为αt[16],可表示为 (11) 算法4加权边界点集成分类算法(CWBUSC(Nall))。 输入:平衡数据集Nall,迭代次数T,子分类器ht(x); ① 初始化样本权重D1(i); /*公式(7)*/ ② fort=1 toTdo ③ calculateet; /*公式(10)*/ ④ ifet>0.5 oret=0 ⑤ break; ⑥ else ⑦ calculateαt; /*公式(11),计算子分类器参数*/ ⑧ updateDt; /*更新样本权重*/ ⑨ end if; ⑩ end for; 通过CWBUSC算法获得了新的分类模型,使得在不平衡数据集的处理过程中获得更加精确的结果。 实验选取标准的UCI数据库中的实验数据,详细信息如表1所示。 表1 实验数据集参数统计表 为验证笔者所提出的样本约简算法的优势与降低数据集不平衡率的有效性,首先采用UCI数据集进行验证,将CWBUSC算法与C 4.5算法、SMOTE-Boost算法、PC-Boost算法、Ada-Boost算法进行对比,比较约简样本的分布情况。 对上面的5个算法进行50次十折交叉检验,并且统计每次实验的结果,求出平均值;对这几种算法的平均值进行比较,得出结果,如表2所示。 表2 算法评测有效性对比Fmeasure指标均值 从表2的Fmeasure值可以看出,CWBUSC算法除了在Letter数据集稍微低于SMOTE-Boost算法和PC-Boost算法之外,在其他6个数据集上均有最佳表现。比较各种算法在7组UCI数据集上的平均值,CWBUSC算法相比其余4个算法的Fmeasure值都高,说明笔者所提方法在少数类分类性能方面有较大的提升。 表3 算法评测有效性对比Gmean指标均值 从表3的Gmean值可以看出,CWBUSC算法在Letter数据集上稍逊于SMOTE-Boost算法和PC-Boost算法,在7个数据集上的平均分类性能上,CWBUSC算法获得了最优精度。 (a) Ada-Boost算法 (b) SMOTE-Boost算法 (c) CWBUSC算法 (e) SMOTE-Boost算法 (f) CWBUSC算法 CWBUSC算法中经过边界点加权再进行欠采样后参与基分类器训练的数据集样本规模与初始数据集相比有所减少。为考察参与训练的不同数据规模比例对算法分类性能的影响,选取Ada-Boost算法、SMOTE-Boost算法和CWBUSC算法3种方法,同时选择以Letter数据集为例,在20%~100%范围内以每次增加20%比例的数据参与基分类器,迭代10次,相关算法的Fmeasure、Gmean均值如图3所示。从图3可看出,随着参与训练数据集比例的增大,无论是Fmeasure还是Gmean值都有所上升,但是随着数据比例的增大,相应的分类性能提升幅度有限。另外,在数据比例为20%至40% 时,3种算法相对应的Fmeasure值和Gmean值几乎是线性提升,这说明过低比例的抽样数据,由于损失太大的原始数据分布信息,会严重影响算法的分类性能。 为了有效解决边界点直接被删除的问题,笔者提出了基于边界点加权的欠采样方法,解决了不平衡数据的处理问题,将多数类样本进行欠采样,最后和少数类达到平衡的状态。该算法的过程主要分为预处理和训练两个部分,预处理阶段主要是将多数类数据进行约简,得到约简后的多数类数据集,与所有少数类数据集组成平衡的训练集,然后融合集成学习的思想,通过分类器加权投票提高整体的分类性能。在UCI数据集上的实验表明,笔者所提算法充分利用了边界点中有用的信息,所得到的样本较好地保持了多数类信息,有效缩小数据集规模,具有较高的执行效率。该算法重点是对已有不平衡数据集进行约简,后续将会重点研究动态不平衡数据集。1.3 约简数据集

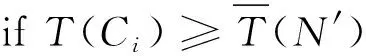
2 基于聚类的加权边界点集成分类方法
3 实 验
3.1 数据集

3.2 实验结果及分析



4 结束语
