面向连续参数的多粒度属性约简方法研究
2021-08-07宋晶晶程富豪王平心杨习贝
吴 将,宋晶晶,2+,程富豪,王平心,杨习贝,4
1.江苏科技大学 计算机学院,江苏 镇江 212100
2.数据科学与智能应用福建省高校重点实验室,福建 漳州 363000
3.江苏科技大学 理学院,江苏 镇江 212100
4.江苏科技大学 经济管理学院,江苏 镇江 212100
粗糙集理论[1]最早是由波兰学者Pawlak 提出的,这一理论近年来在数据挖掘、人工智能、决策分析等领域[2-4]受到了广泛关注。在粗糙集理论与方法中,属性约简问题[5-10]一直是众多学者关注的焦点。作为一种特征选择机制,约简的目的是获得满足给定约束条件的最小属性子集,进而达到降低不确定性、提升学习器泛化性能等目的。在数据分析中,属性约简中的约束条件往往可以通过一些度量准则进行构造,如近似质量、条件熵等[6,8]。
经典粗糙集方法仅能处理符号型数据,但在解决实际应用问题时,连续型数据是广泛存在的。因此已有诸多学者构建了很多拓展的粗糙集模型以用于分析及处理连续型数据:如基于高斯核函数的模糊粗糙集[10]和基于邻域关系的邻域粗糙集[5]。这两者均可以视作是使用参数化的方法构造二元关系及相应的粗糙集模型。但值得注意的是,利用这些参数化粗糙集进行属性约简问题的研究时,会带来诸如参数计算量过大等一系列问题。鉴于此,已有学者将参数视为粒度的表现形式[11-13],对多粒度环境下的属性约简问题进行了初步探索。然而,已有的研究成果仍然存在一些可以提升的空间:(1)在多个参数所对应的多粒度结构下进行约简求解时,一种常用的策略是针对于每一个参数,分别求解约简。显然,当参数体量较大时,这一过程会带来较高的时间消耗。(2)在多个不同的参数下,可以得到多个约简,当参数之间差异性较小时,这些约简结果有可能存在较大的差异性。换言之,单个约简一般只能表示某个粒度意义下满足约束条件的最小属性子集,而对于其他相邻参数所对应的粒度,约简的结果有可能大相径庭。因此,多参数意义下的多个约简结果并不具有普适性。
为了解决上述问题,本文从连续参数的视角出发,提出了多粒度属性约简的一种新模式,主要包括两部分内容:首先在一个连续参数区间内,构造了多粒度属性约简的约束条件,然后利用前向贪心搜索策略,设计了求解多粒度约简的算法。与多个参数意义下分别求解约简的模式不同,连续参数下多粒度属性约简的目的不是分别针对每个参数进行约简求解,而是根据多粒度约束条件求得一个约简,进而有望降低约简求解的时间消耗。
1 基础知识
1.1 邻域粗糙集
在粗糙集中,决策系统可以表示为一个二元组DS=
在粗糙集理论中,信息粒化[14-19]的进程一般是通过利用条件属性所提供的信息来构建二元关系,进而能够对论域中的样本进行区分。以邻域粗糙集模型为例,可以通过在论域上使用邻域关系[5]来进行信息粒化,邻域关系的定义如下所示。
定义1给定决策系统DS=
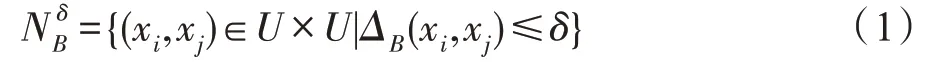
其中,ΔB(xi,xj)表示利用条件属性子集B所提供的信息得到的样本xi与xj之间的距离。
使用如式(1)所示的邻域关系对论域进行信息粒化可得到所有样本的邻域,∀xi∈U,xi的邻域可以表示为δB(xi)={xj∈U|ΔB(xi,xj)≤δ},δB(xi)中的样本被视作与xi是不可区分的,而δB(xi)之外的样本则被视作与xi是可区分的。因此,每个样本的邻域即表示了一个信息粒,所有样本的信息粒的合集就是信息粒化的结果。一般来说,如果半径δ较小,那么利用式(1)将会得到较细的信息粒化结果;反之,将会得到较粗的信息粒化结果。为了量化地描述信息粒化结果的粗细程度,可以使用如下定义所示的粒度概念。
定义2[13]给定决策系统DS=

其中,|X|表示集合X的基数。
因为式(1)所示的邻域关系满足自反性,所以在定义2中,有成立。在特殊情况下:(1)当邻域关系为ω={(xi,xi)∈U×U:∀xi∈U} 时,可得到最细的信息粒,此时粒度取最小值1/|U|;(2)当邻域关系为η={(xi,xj)∈U×U:∀xi,xj∈U}时,可得到最粗的信息粒,此时粒度取最大值1。
定义3[8-9]给定决策系统DS=

作为粗糙集理论中属性约简中常用的度量准则,近似质量的形式化描述如定义4 所示。
定义4[20]给定决策系统DS=

条件熵作为另一种常用的度量,它能反映条件属性相对于决策属性的鉴别能力。根据实际应用的不同,条件熵有很多定义的形式[17-19],其中一种具有单调性的条件熵定义如定义5 所示。
定义5[21]给定决策系统DS=
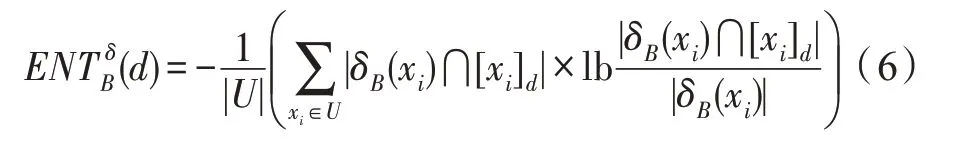
其中,[xi]d表示与样本xi属于同一决策类的样本的合集。
条件熵的值越小,则条件属性相对于决策属性的鉴别能力越强。
1.2 多粒度属性约简
属性约简是粗糙集理论研究中的一个核心问题,其本质是去除条件属性中的冗余和不相关属性,以得到满足给定约束条件的最小属性子集。为了更深入地理解属性约简的本质,Yao 等人[6]从粒计算角度出发,给出了属性约简的形式化方法。但由于Yao等人提出的属性约简定义只适用于描述单个粒度下的约简,而单粒度约简无法为参数化粒度的选择提供有力的支撑,且无法展现不同粒度所对应约简的性能的变化趋势[11],因此,Jiang 等人[12]采用邻域的方法,给出了一种多粒度属性约简的形式化描述方法,如定义6 所示。
定义6[12]给定决策系统DS=
(1)Bt满足约束条件;
显然,定义6 所示的多粒度约简是多个单粒度约简的合集。其中,φ代表度量准则,可表示由近似质量构造的约束条件或者由条件熵构造的约束条件。当使用近似质量构造的约束条件时,为,此时每一单粒度约简是一个能够保证当前粒度下近似质量不会被降低的最小属性子集Bt;当使用条件熵构造的约束条件时,φδt为,此时每一单粒度约简是一个能够保证当前粒度下条件熵不会被升高的最小属性子集Bt。
目前,前向贪心搜索策略在约简的求解问题中受到众多学者的青睐,这一方法在每次迭代的过程中将属性重要度最大的属性加入到约简集合中,直至所选择的属性子集满足约束条件。鉴于此,可以采用如定义7 所示的形式对候选属性进行评估。
定义7给定决策系统DS=
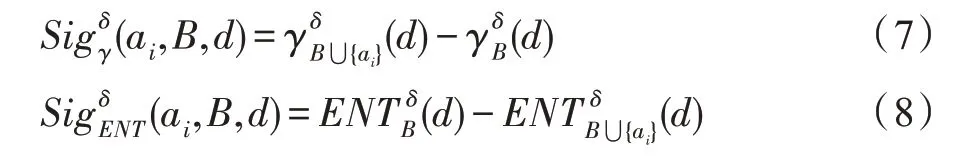
式(7)表示利用近似质量计算属性重要度,若加入ai后近似质量的值越大,则说明ai的重要度越高;式(8)表示利用条件熵计算属性重要度,若加入ai后条件熵的值越小,则说明ai的重要度越高。
实际上,定义6 所示的多粒度约简是多个单粒度约简的合集,因而多粒度约简求解可通过重复单粒度约简求解过程来实现。采用前向贪心搜索策略,运用定义7 所示的属性重要度,可设计出如算法1 所示的多粒度约简求解过程。
算法1离散参数下的多粒度约简合集求解算法

利用算法1 求解多粒度约简的时间复杂度为O(s×|U|2×|AT|2),主要是因为:(1)在单个粒度下计算邻域的时间复杂度为O(|U|2×|AT|2),而在最坏的情况下,每个条件属性都需要被评估且加入约简集合中,即AT中没有冗余的属性,则单粒度下求解约简的时间复杂度为O(|U|2×|AT|2);(2)对于求解s个粒度下的约简是将单粒度求解约简的过程重复s次,因此求解多粒度约简的时间复杂度为O(s×|U|2×|AT|2)。
2 连续参数意义下多粒度属性约简
不难发现,算法1 所示的多粒度约简求解过程是在离散化参数的基础上实现的,这种重复求解单个参数所对应约简的策略,当参数体量过大时会导致求解约简的时间消耗急剧增加。鉴于此,本文将提出一种基于连续参数的多粒度属性约简框架:给定参数区间[δ1,δs],设计相应的约束条件求得约简,期望用此约简结果表示在整个区间[δ1,δs]下求得的各个多粒度约简,而不再针对连续参数中的每一个参数进行求解约简得到的多粒度约简结果。
在连续参数下多粒度求解约简的过程中,如何设计和求解约束条件φ是一个关键问题。从算法1中可以看出,多粒度约简合集的求解是通过重复求解单粒度约简来实现的。针对连续参数下约简求解问题,在仔细分析粒度的公式(定义2)的基础上,可以观察到,对于给定的参数区间[δ1,δs],利用最小参数δ1可获得一个最细粒度,利用最大参数δs可获得一个最粗粒度。因此,本文将使用最细粒度和最粗粒度下度量准则的融合策略来进行属性约简。
定义8给定决策系统DS=
(1)B满足约束条件;
(2)∀B′⊂B,B′不满足约束条件。
在定义8 中,与定义7 类似,其中,φ代表度量准则,可表示由近似质量构造的约束条件或者由条件熵构造的约束条件。但与定义7 不同,当使用由近似质量构造的约束条件时,且”,即定义8 给出的约简是一个能够保证在连续参数上,利用δ1和δs计算出的近似质量不会降低的最小属性子集B;当使用由条件熵构造的约束条件时,为“且”,即定义8 给出的约简是一个能够保证在连续参数上,利用δ1和δs计算出的条件熵不会增大的最小属性子集B。
运用定义8 和以上对约束条件的构造,可设计出如算法2 所示的连续参数下多粒度约简求解算法。
算法2连续参数下的多粒度约简求解算法


算法2 的时间复杂度为O(|U|2×|AT|2)。对于计算连续参数下的约简,只需执行一次算法2,但对于算法1 而言,需要针对s个参数进行约简的求解,此时算法1 将被执行s次。显然,当s>1 时,算法2 求解多粒度约简的时间复杂度小于算法1 求解多粒度约简的时间复杂度,因此从这一角度来看,采用算法2 有望降低求解多粒度约简的时间消耗。
3 实验分析
为了验证算法2 的有效性,在连续参数下求解多粒度的约简,本文参考了文献[7]中选取半径区间的方法并使用了该文献实验的8 组数据。数据的基本描述如表1 所示。
文献[7]在选取半径和半径区间的过程中,使用了100 个不同半径δ=0.01,0.02,…,1.00,并计算了相应的近似质量。对于每一个数据集,选择了近似质量大于0.1 的半径区间,这主要是因为在粗糙集理论中,较小的近似质量对刻画确定性的意义不大。使用该方法选取各个数据集的10 个半径和半径区间,具体描述如表2 所示。
值得注意的是,在连续参数下求得的一个多粒度约简是保持近似质量不会降低或条件熵不会增大的最小属性子集。但是,经过大量实验发现,连续参数下求解多粒度约简的约束是很严格的,不利于冗余属性的删除,故可通过控制阈值的方式来控制约简的约束条件[19]。为了能够更有效进行实验对比分析,阈值ε的取值分别为5%和10%。故本次实验中约简的约束条件为:当使用由近似质量构造约束条件时,形如“且”;当使用由条件熵构造的约束条件时,形如“且”。为了验证新提出算法的有效性,实验采用了五折交叉验证的方法。在上述的8 组数据集中,利用五折交叉验证,分别计算了离散参数下和连续参数下求得约简的时间消耗与约简中属性所提供的分类精度,其中在计算分类精度时使用的方法分别为K最近邻算法(K-nearest neighbor,KNN)与支持向量机(support vector machine,SVM)。
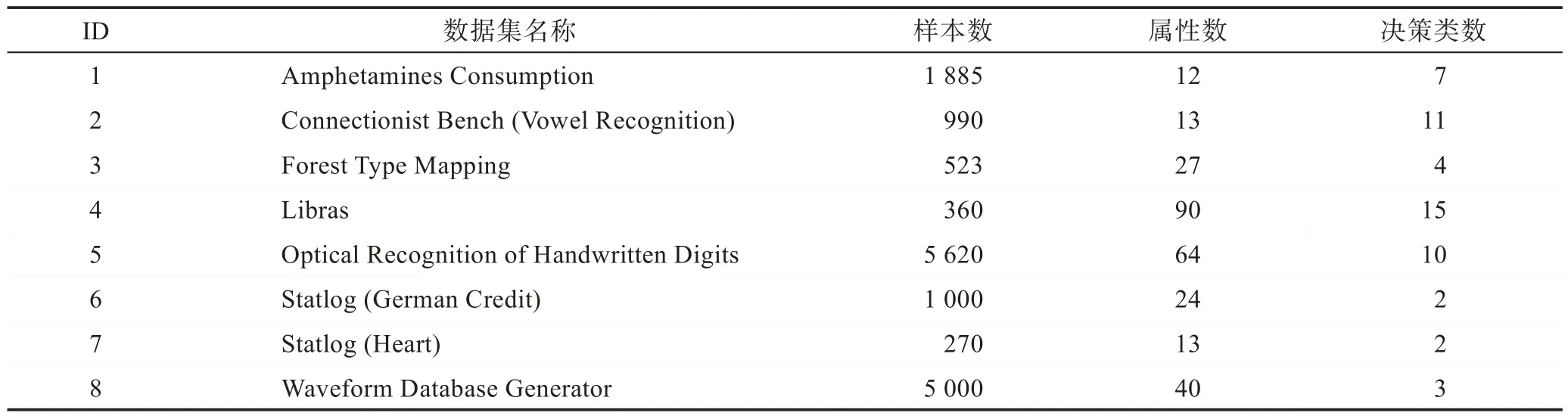
Table 1 Description of data sets表1 数据集描述
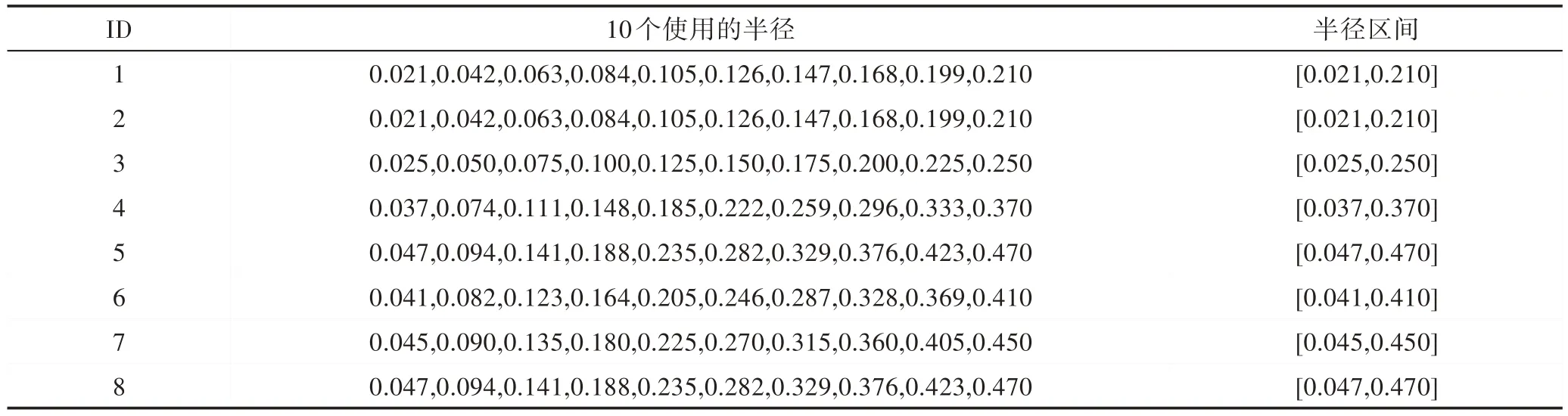
Table 2 Used radii and radii interval for data sets表2 数据集使用的半径和半径区间
3.1 时间消耗对比
观察表3,不难得出以下结论:
(1)无论是使用算法1 还是算法2,相较于使用条件熵作为度量准则,在使用近似质量作为度量准则时,计算约简的时间消耗较高。通过观察实验结果,认为主要是因为在使用近似质量作为度量时,约简集合中包含属性个数往往比使用条件熵时所求得的约简集合中包含的属性个数更多,此时带来了属性评估及属性选择迭代次数的增多。
(2)使用算法2 计算约简的时间消耗显著低于使用算法1 计算约简的时间消耗。这是因为当给定10个半径时,算法1 需要重复10 次前向贪心搜索策略,从而获得多粒度下的约简合集。然而,在连续参数下求解约简只需要执行1 次就可以得到多粒度约简结果。以“Amphetamines Consumption(ID:1)”数据集为例,使用近似质量作为度量时,约束条件的阈值为5%和10%的算法1 计算多粒度的约简合集消耗的时间为34.975 7 s 和34.335 6 s,约束条件的阈值为5%和10%的算法2 计算多粒度约简消耗的时间分别为7.796 5 s 和7.559 6 s。很明显,算法1 的时间消耗大于算法2 的时间消耗。
(3)当约束条件的阈值设置为5%时,计算约简的时间消耗一般要高于约束条件的阈值为10%时计算约简的时间消耗。这是因为相对于阈值为5%的约束条件而言,阈值为10%时的约束更为宽松,因而约简求解时属性评估及属性选择的迭代次数减少了,带来了更低的时间消耗。以“Statlog(German Credit)(ID:6)”数据集为例,在算法2 中使用条件熵作为度量时,约束条件的阈值为5%计算约简的时间消耗为4.313 6 s,而约束条件的阈值为10%计算约简的时间消耗为4.136 4 s。
3.2 分类精度对比
通过表4 和表5 展示的结果,不论采用KNN 分类器还是SVM 分类器,不难得出以下结论:
(1)无论是使用近似质量还是条件熵作为度量准则时,在大多数情况下,算法2 求得约简中属性所提供的分类精度比算法1 求得约简中属性所提供的分类精度高。这说明算法2 的连续参数下求得的多粒度约简能够带来更好的分类性能。以“Libras(ID:4)”数据集为例,使用近似质量作为度量准则并将约束条件的阈值设为10%,采用KNN 分类器,算法1 求得约简中属性所提供的分类精度为0.715 8,算法2 求得约简中属性所提供的分类精度为0.775 0;采用SVM 分类器,算法1 求得约简中属性所提供的分类精度为0.443 6,算法2 求得约简中属性所提供的分类精度为0.602 8。
(2)在大多数情况下,约束条件的阈值为5%和10%求得约简中属性所提供的分类精度相差甚微。以“Forest type mapping(ID:3)”为例,算法2 使用近似质量作为度量准则时,使用KNN 分类器,约束条件的阈值为5%和10%求得约简中属性所提供的分类精度分别为0.858 5 和0.858 5。

Table 3 Comparison of elapsed time of obtaining reduct表3 求解约简的时间消耗对比 s

Table 4 Comparison of classification accuracies based on KNN表4 KNN 分类器下的分类准确率对比
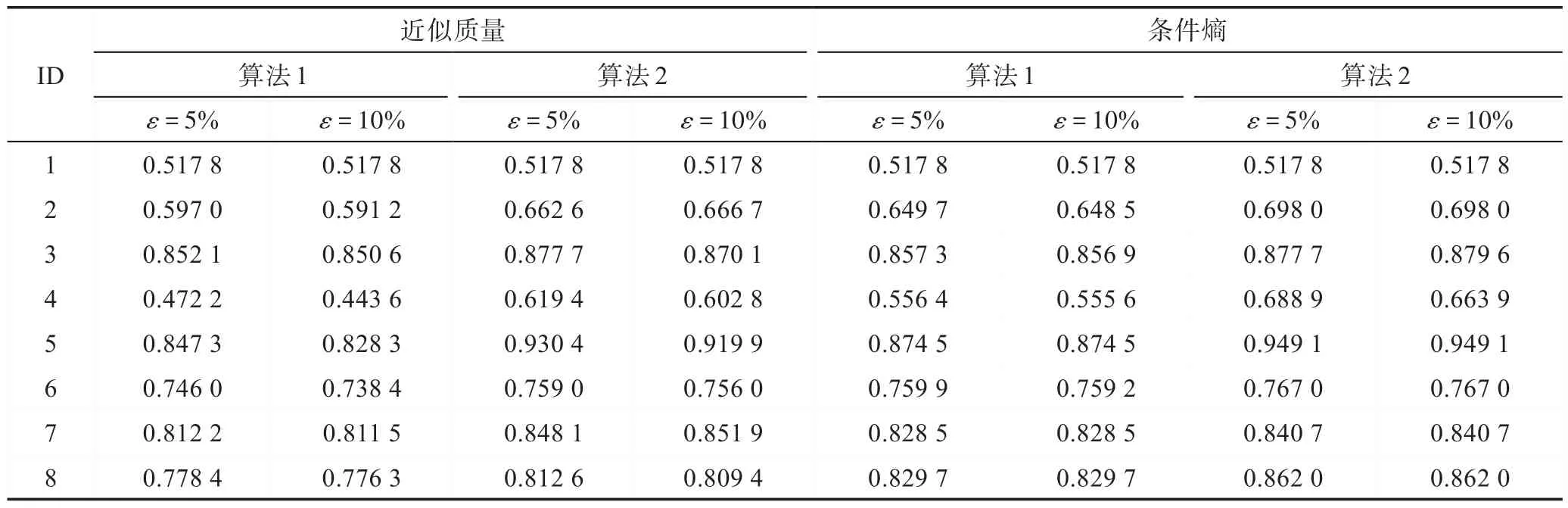
Table 5 Comparison of classification accuracies based on SVM表5 SVM 分类器下的分类准确率对比
4 结束语
与传统约简求解方法不同,为了降低多粒度约简求解的时间消耗,本文提出了一个面向连续参数的多粒度属性约简框架。首先构造了连续参数下求解约简的约束条件,然后利用前向贪心搜索策略,设计了求解连续参数意义下多粒度约简的算法,最后将新提出的算法与离散参数意义下约简的求解方法进行了对比。实验结果表明,所提算法不仅能够有效地降低约简求解的时间消耗,而且所求得的约简亦能够提供满意的分类性能。在本文工作的基础上,可就以下的问题展开进一步的探讨:
(1)文中仅使用近似质量和条件熵作为度量准则,未来工作中可以进一步考虑其他度量方式,如邻域鉴别指数[8]、决策错误率[20]等。
(2)本文仅使用了邻域粗糙集模型来构建连续参数下多粒度求解约简的方法,可以将连续参数的思想拓展引入到其他的粗糙集模型,如模糊粗糙集模型。
