区域能量聚焦技术中超稀疏阵列优化算法
2021-09-02杨仲平周青松张剑云
杨仲平,周青松,张剑云
(国防科技大学 电子对抗学院,安徽 合肥 230031)
传统的电子战采用的干扰技术大多是向干扰区域“粗放式”投递干扰信号,在战场中形成以目标点为中心的扇形干扰区,然而这种干扰方式往往会对目标点附近的我方设备造成电磁误伤。为解决这一问题,美国国防高级研究计划局(DARPA)提出了精确电子战的概念[1],其基本思想是在干扰区域上方设置一组超稀疏阵列,采用区域能量聚焦技术对指定目标实施“外科手术式”精确干扰,同时不影响目标附近友邻设备的正常工作[2]。
自精准电子战的概念提出以来,国内外文献中多采用设计干扰信号的方法以实现精确干扰[3-5],尚无涉及超稀疏阵列优化的研究。然而在某些情景下,这些算法限于阵列位置无法达到精确干扰的最大效能,从而导致干扰资源的浪费。当采用无人机集群实施精确干扰时,通常设置无规律分布的随机阵型,以保证无人机灵活的拓扑结构和较高的战场生存能力[6],具有较强突防能力的无人机通过成熟的航迹规划方法可以到达指定位置[7]。在此背景下,研究超稀疏阵列优化问题可行且有意义。在阵列优化问题中,目前提出的解析方法多用于求解非等间隔线阵的最优距离以及非均匀圆阵的最优夹角[8-9]。这类模型通过松弛方法可转化为凸或拟凸问题,从而得到方便求解的形式。但这种方法应用的范围有限,且优化效率较低,不适于求解目标函数及约束条件形式复杂的阵列优化模型。因此,相关学者多采用智能算法对阵列优化问题进行研究,其中粒子群算法具有收敛速度更快、不易陷入局部最优、易于融合其他算法等优良性质,并且能够对复杂模型的解空间进行启发式搜索,因而被广泛用于稀布阵列方向图综合的优化问题[10-14]。其中,文献[11]融合了混沌优化算法的优点,提出一种改进粒子群算法,在有效生成多零陷的同时较好地抑制了旁瓣;文献[12]在稀布阵列优化问题中结合粒子群算法和二阶锥规划方法,求解了具有复杂约束的多目标优化模型,得到了所需的方向图以及更低的旁瓣;文献[13]提出一种结合凸优化方法的粒子群算法,改善了线型稀疏阵列的多项旁瓣指标;文献[14]对稀疏阵列的位置、角度和相位采用粒子群算法进行联合优化,充分利用阵列的优化维度,减少了阵元数量并满足稀疏阵列旁瓣和交叉极化的性能要求。
针对上述问题,笔者首先根据精确电子战的空间模型,建立干扰信号与阵元位置的联合优化模型,以最大化精确干扰效能。由于干扰信号的恒模约束以及超稀疏性约束导致了问题的非凸性及复杂性,所以采用粒子群算法对阵列进行优化;然后针对每次迭代的阵列,继续求解干扰信号设计子问题,以子问题的目标值作为粒子群算法的适应度,这种基于粒子群算法的超稀疏阵列优化方法最终可以实现超稀疏阵列与干扰信号的联合优化;最后,通过多组仿真对比了优化前后的精确干扰效果,并表明该算法在无人机平台有无定位误差两种情况下,均较现有算法具有更优性能,在精确电子战中具有实际意义。
1 精确电子战空间模型

图1 精确电子战空间模型
在图1所示的空间坐标系中,目标点坐标为rT,保护点坐标为rPi,其中rT∈R1×3,rPi∈R1×3。
考虑到实际情况中对敌方设备的位置探测误差及设备尺寸,分别以目标点与保护点为圆心设置圆形目标区域ΩT与保护区域ΩPi,且ΩT与ΩPi均处于xOy平面。搭载干扰阵元的无人机平台共计M个,各阵元位置ri∈R1×3。为方便表达,以向量形式R=[(r1)T,(r2)T,…,(rM)T]T∈RM×3表示阵列位置。各阵元发射的信号xm(t)∈C,m=1,2,…,M,则该阵列在当前采样时刻tn的信号可以用如下向量形式表示:
x=[x1,x2,…,xM]T。
(1)
信号在空间传播的导向矢量为
(2)
其中,f0为发射信号的载波频率,‖·‖表示二范数。τm(r)=‖rm-r‖/c,为信号从rm处至r处的传播延时,c=3×108m/s,1/‖rm-r‖算子为信号在空间的传播衰减。阵列在点r处的合成信号可以表示为
S(R,r)=a(R,r)Hx。
(3)
阵列在r处的功率为

(4)
由此可得在区域Ωs处的能量为
(5)
为求式(5)的解析形式,将圆形区域离散为N个网格。当N→∞时,可以用其几何中心rσi代替该网格σi的所有点。设每个网格面积S=Δσ,则可求得式(5)的解析形式:
(6)
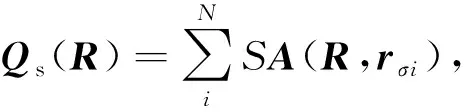
2 超稀疏阵列优化原理
2.1 模型公式化表达
精确电子战的目标是实现对目标区域的干扰与保护区域的能量抑制,评价准则可以表示为二者区域的能量差值。因此,由式(6)可得评估准则O:
O=xHQT(R)x-xHQP(R)x,
(7)
其中,QT(R)=∑QTi(R),是目标区域聚焦单元ΩT功率乘子的求和形式,是关于阵列位置R的变量;同理,QP(R)是保护区域的功率乘子求和形式。针对式(7)提出的精确电子战评估标准及约束条件,可将优化问题表述如下:
(8a)
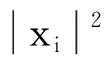
(8b)
‖ri-rj‖2≫λ/2 ,
(8c)
ri∈R 。
(8d)
约束式(8b)表示各独立的无人机搭载阵元采用最大功率,并进行归一化处理。约束式(8c)是使阵列位置R满足阵列的超稀疏性约束,即任意阵元距离远大于信号半波长。约束式(8d)表示各阵元位置应在某一特定范围。
2.2 求解子问题的MFED算法
考虑到该问题是关于信号x与阵列位置R的多变量联合优化问题,下面对式(8)进行简化:
(9)
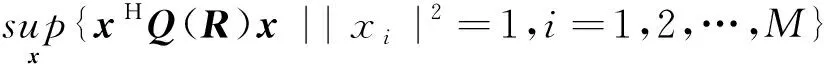
(10)

(11)

2.3 超稀疏阵列优化的PSO-MFED算法
当采用MFED算法时,对于确定的超稀疏阵列布局可设计出相应的干扰信号,并评价当前阵列位置下的目标值。因此,可以认为通过MFED算法能够找到一种干扰信号x与阵列位置R的关系。式(8)即转化为关于阵列位置R的优化问题,即
(12)
由于MFED算法是一种迭代求解方法,难以得到关于x(R)的表达式,且式(12)中约束形式较为复杂,采用解析手段难以求解,因此采取粒子群算法对该问题进行求解。粒子群算法是一种模拟鸟群觅食行为的仿生算法,通过对整个群体的信息共享,利用随机搜索寻找全局最优解的求解策略[15]。该算法中,每个优化问题的潜在解被模拟为搜索空间中的一个“粒子”,并将优化问题的准则作为该粒子的适应度。每个粒子具有3个属性,即位置、速度与飞行经验,其中位置表示粒子当前解,速度决定解的搜索方向和距离,飞行经验是通过比较适应度得到的该粒子目前为止搜寻到的最优位置pbest。所有粒子通过“信息共享”得到该群体目前为止搜索到的最优位置gbest。粒子群算法通过迭代来更新每个粒子的速度和位置,重新计算pbest及gbest。每个粒子的速度及位置更新规则为
vi=vi+φ1r1(pbesti-di)+φ2r2(gbesti-di) ,
(13)
di=di+vi,
(14)
其中,φ1、φ2是学习因子,r1、r2是区间(0,1)内的随机数,di是粒子当前位置,vi为粒子速度。为使算法模型具有良好的收敛性,通常在速度更新公式的基础上引入收敛因子K,因此式(13)修正为
vi=K[vi+φ1r1(pbesti-xi)+φ2r2(gbesti-xi)] 。
(15)
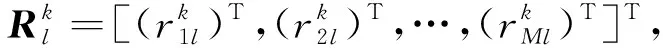
2.4 超稀疏阵列优化算法流程
PSO-MFED算法流程如下。
(1) 设置k=0,在超稀疏阵列的各阵元初始位置附近随机生成L个满足约束条件的阵列粒子。
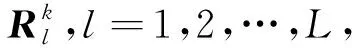

(5) 根据式(15)计算每个粒子的速度,根据式(14)计算每个粒子的新位置。若新位置不满足式(12)中的约束条件,则初始化该粒子。
(6)若当前gbestk或k值满足结束条件(达到预设的目标值或迭代数),则算法终止并输出gbestk所对应的阵列位置;否则,跳转至步骤(2)。
3 仿真结果及分析
3.1 PSO-MFED与MFED算法效果对比
为说明上述算法的有效性,在主频为1.70 GHz的i5-4210U型CPU,RAM为4 GB的硬件环境下,依托MATLAB R2016a软件平台进行实验。实验设置如下仿真情景:xOy平面内关注范围为[-50 m,50 m]×[-50 m,50 m],保护区与目标区均位于该平面内;目标中心位于坐标原点,4个保护中心坐标分别为(20 m,25 m,0 m)、(-20 m,10 m,0 m)、(-15 m,-25 m,0 m)、(10 m,-20 m,0 m),目标区域半径rT=5 m,保护区半径rP=2 m。区域离散化网格尺寸为0.25 m×0.25 m。载有超稀疏阵列的无人机群位于距xOy平面d=2 000 m的同一平面内,M=10,发射信号载频f0=1 GHz。位置优化范围约束R=(-30 m,30 m)×(-30 m,30 m)的正方形区域,超稀疏阵列之间的阵元间距满足‖ri-rj‖2≥20λ(i=1,2,…,M,j=1,2,…M)。
在PSO-MFED算法中,设置粒子群算法种群数量L=20,式(15)中收敛因子K=0.729,学习因子φ1=2.1,φ2=2[16],r1和r2由MATLAB软件中的rand函数随机产生。算法步骤(2c)中的迭代停止参数Γ=10-5,粒子最大搜索速度vmax=0.5 m/s,粒子群算法迭代停止条件kmax=100。
在一定的阵元位置下,采用MFED算法得到干扰信号,并由式(6)计算xOy平面内各网格点的能量。为方便对比,各点干扰能量均采用文献[5]的方法,由1/d2进行归一化处理。随机给定3组初始布局,采用MFED算法得到如图2中(a)~(c)所示的能量分布图,在相应的初始阵列下采用PSO-MFED算法得到xOy平面内能量分布图,如图2(d)~(f)所示。
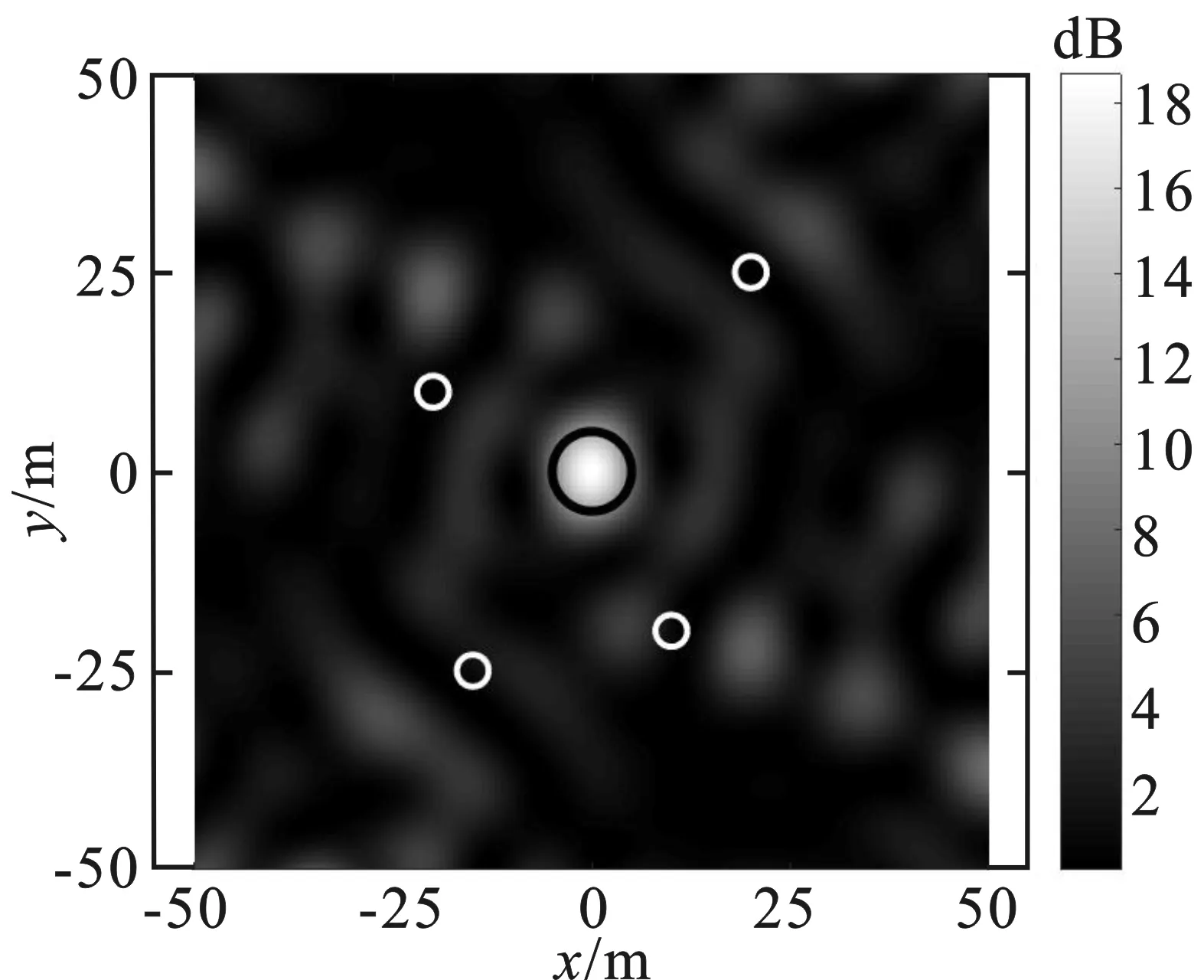
(a) 初始阵列Ⅰ下能量分布(MFED)
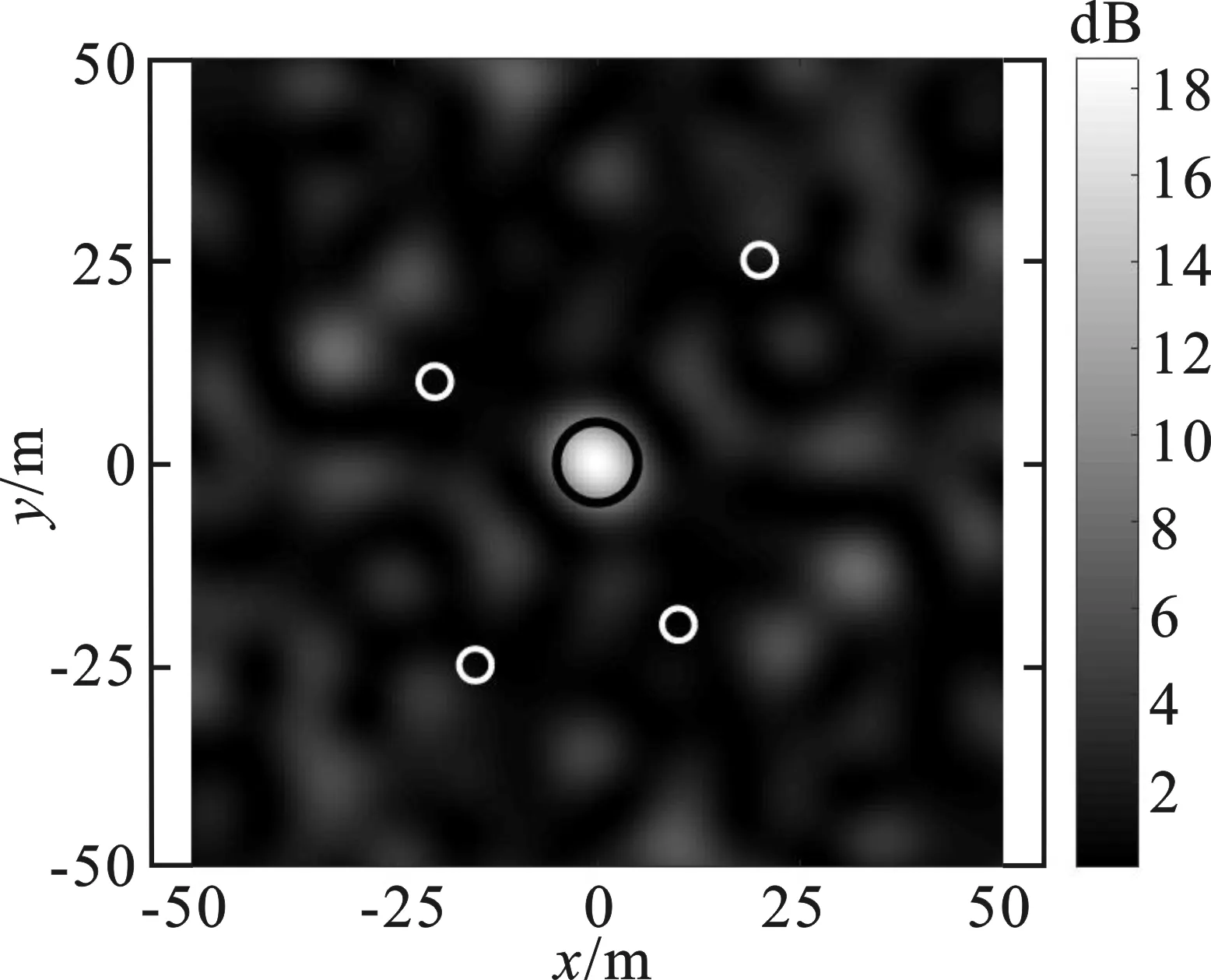
(b) 初始阵列Ⅱ下能量分布(MFED)
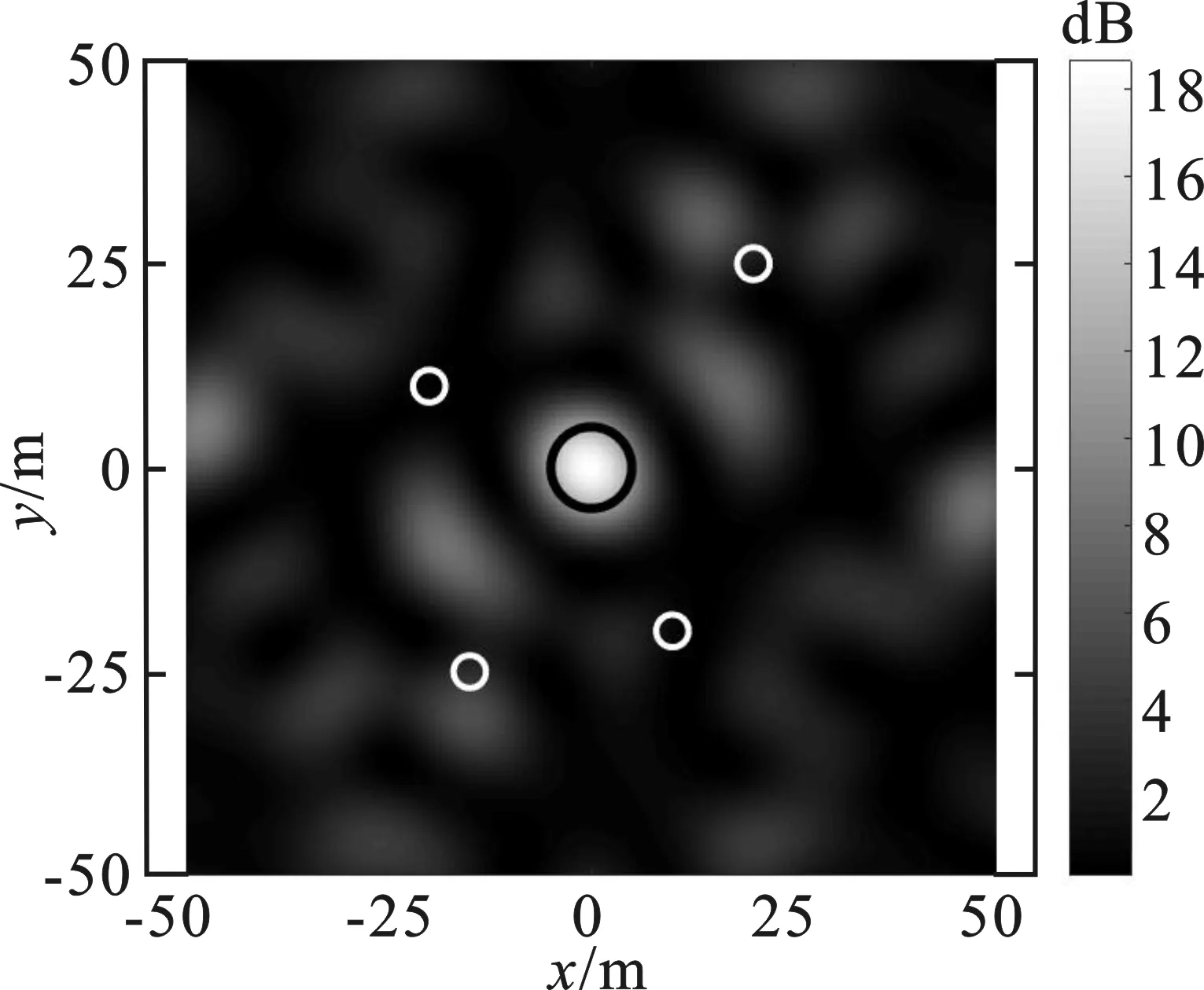
(c) 初始阵列Ⅲ下能量分布(MFED)

(d) 阵列I优化后能量分布(PSO-MFED)
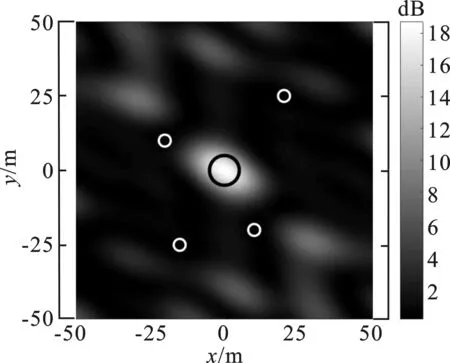
(e) 阵列II优化后能量分布(PSO-MFED)
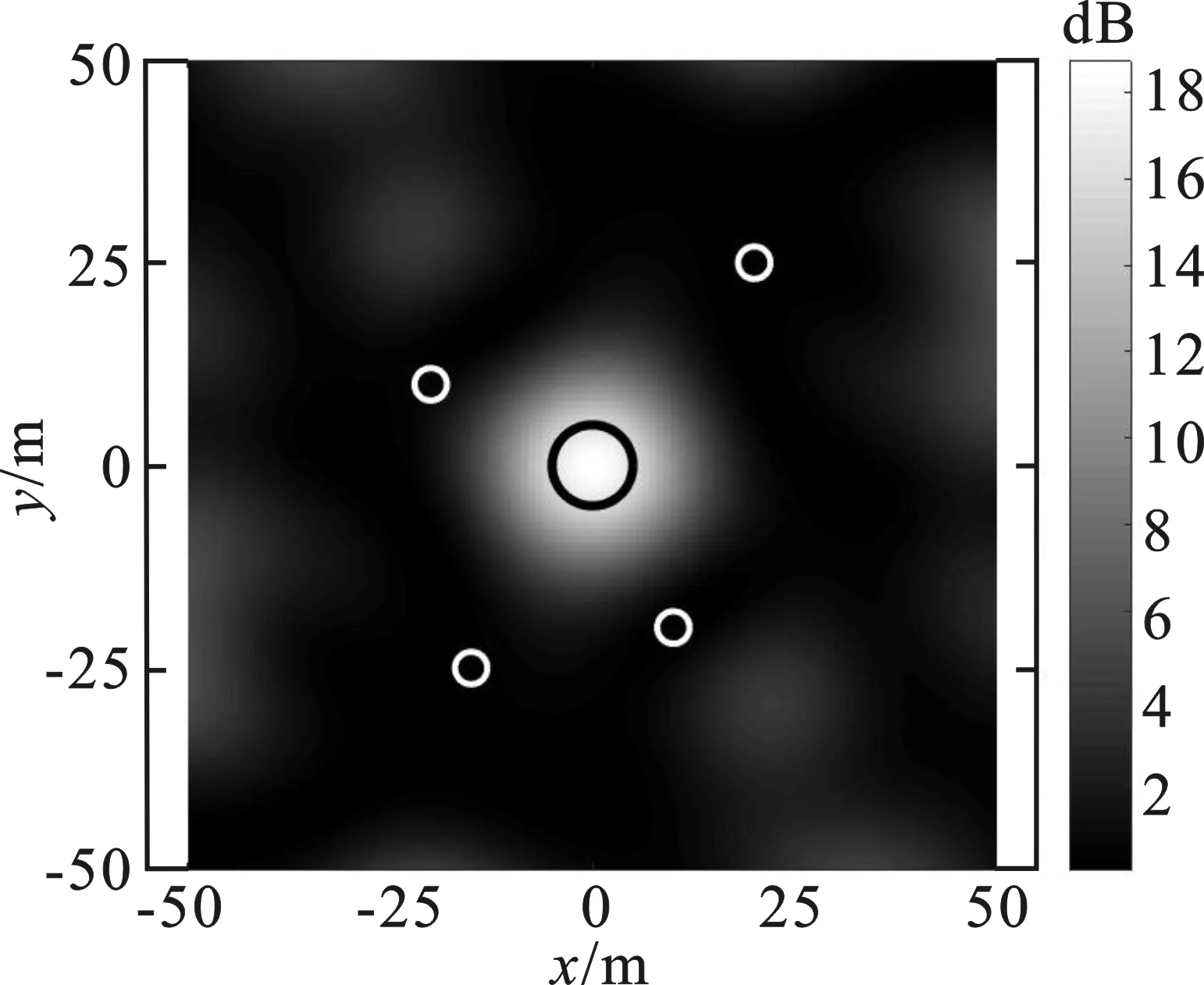
(f) 阵列III优化后能量分布(PSO-MFED)
图2中黑色圆线代表目标区域,白色圆线代表保护区域,浅色区域表示能量较高,深色区域表示能量较低。从图2中明显可见,经阵元位置优化后,目标区域内能量更为聚集,保护区域内能量进一步降低,精确干扰效果更好,证明了超稀疏阵列优化算法的有效性。
3.2 无定位误差下区域能量聚焦性能分析
当各无人机平台无定位误差时,表1给出如下性能指标:目标区域内能量的最小值ET,保护区域内能量的最大值EP,目标区域内平均能量EaveT,保护区域内平均能量EaveP,有效干扰率ηT与误干扰率ηP。其中EaveT、EaveP、ηT、ηP定义如下:
(16)
其中,NT、NP分别表示目标区域和保护区域内离散网格点的个数,I(·)表示单位阶跃函数,cT=12 dB,cP=1 dB。
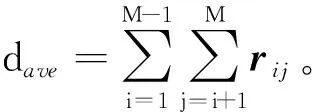
阵列优化的目的是减小阵元平均距离,在一定程度上降低阵列的稀疏性,以减小栅瓣能量,进而在能量关注范围形成更接近精确干扰目的的方向图。从表1数据可以看出,经过超稀疏阵列布局的优化,使得有效干扰率和误干扰率在性能上有大幅提升,能更有效地干扰敌方设备且更好保护我方设备,满足精确电子战的目标。
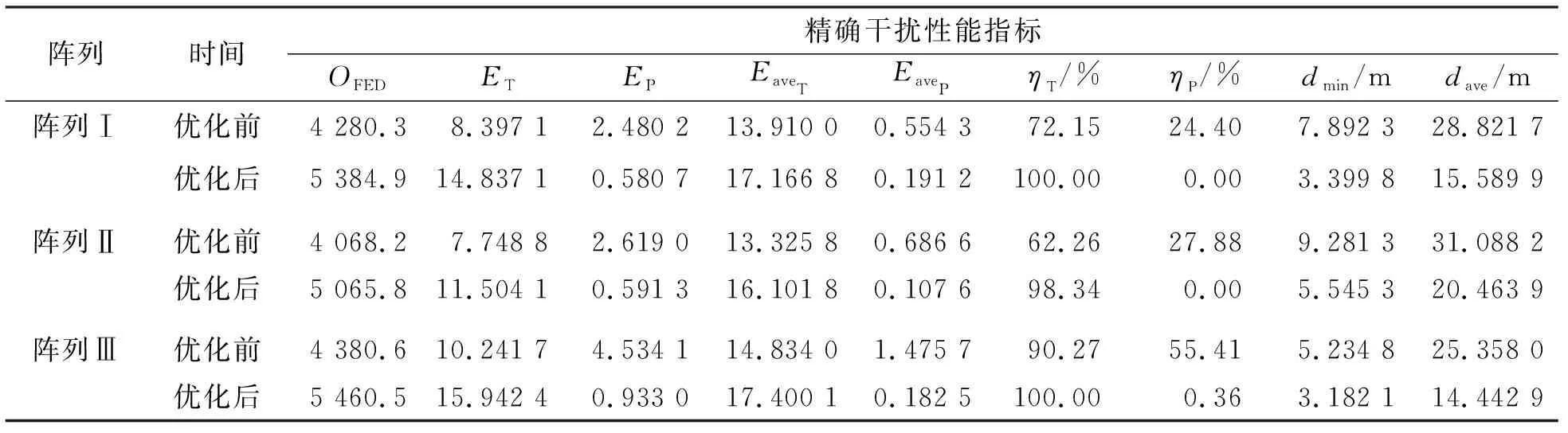
表1 无定位误差及不同初始设置下精确干扰性能指标
3.3 有定位误差下区域能量聚焦性能分析
由于无人机平台不可避免地存在定位误差,应对有定位误差下的布局进行分析,进一步探究实际情况中的性能。当前采用RTK技术的无人机平台可以将静态定位误差限制在厘米级范围内。对各独立的无人机平台的真实位置r′i进行合理假设:即r′i在以无定位误差的位置r′i为球心,半径为r的球体内均匀分布。表2设置3组误差实验,对初始布局I及其优化后的结果进行分析。
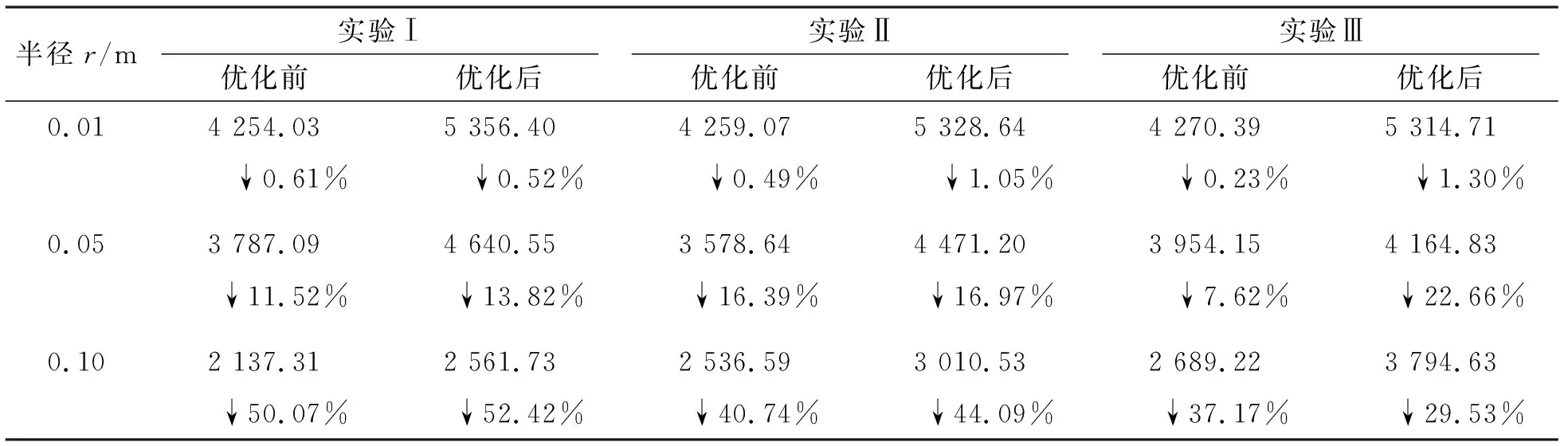
表2 有定位误差下精确干扰指标
尽管无人机平台的定位误差对精确干扰效果存在一定影响,但从表中可见,当存在相同等级的定位误差时,优化后的阵列在干扰准则上仍优于原阵列,进一步证明了阵列优化的必要性及有效性。当存在1~5 cm的定位误差时,干扰准则的下降在可接受范围内;但当定位误差超出厘米级范围时,性能恶化明显。
4 结束语
笔者以无人机集群实施精确电子战为应用背景探究超稀疏阵列优化问题,提出了PSO-MFED超稀疏阵列优化算法,最终实现干扰信号与阵列布局的联合优化。其本质上是增加了模型的优化维度,从而使得精确干扰各项评价指标均有较大提升。仿真结果表明,该算法在有无定位误差的情况下,各项指标均优于仅对干扰信号相位进行设计的算法,能有效地提高精确干扰性能,也突显出超稀疏阵列优化的必要性。该算法是一种随机搜索算法,给定不同的初始布局,得到的解在目标准则上十分接近,说明建立的准则关于阵列在其解空间上存在多个鞍点,该算法求得的阵列是局部最优。所以在给定目标区域和保护区域的情景下,无人机集群干扰存在多种阵列设置方案,该算法在实际应用中具有较强的灵活性和实用性。
