多星敏感器协同观测的短弧关联算法
2021-09-02黄秋实张雅声
黄秋实,张雅声,冯 飞
(1.航天工程大学 航天指挥学院,北京 101400;2.中国人民解放军61646部队,北京 100085)
随着航天器和空间碎片的增加,日益拥挤的空间环境成为各国争相抢夺的宝贵战略资源,其中地球同步轨道(GEosynchronous Orbit,GEO)的卫星往往承担着通信、导弹预警、数据中继、广播等重要任务,具有极高的战略价值[1]。对地球同步轨道目标的监视是空间态势感知的重要一环,关系着国家的太空安全。目前,中国对地球同步轨道目标的探测及监视主要依赖于地基光学监视系统[2],地基监视系统工作会受到大气及气象条件的影响,无法全天时观测,特别是由于地理和政治因素,中国不具备美国的全球布站条件。相比于地基观测,天基监视系统不受大气、地理位置的制约,具有观测距离远、设备复杂度低、功耗小等优势[3]。美国以光学卫星组网构建天基空间目标监视系统(Space-Based Surveillance System,SBSS)[4],耗资巨大。中国的天基目标监视系统有待发展。基于星敏感器的空间目标泛在感知即挖掘星敏感器在定姿任务中拍摄的空间目标信息,利用在轨卫星数量多、星敏感器资源丰富的优势,在完成星敏感器定姿任务的同时实现对空间目标的监视[5],可节约发射专用监视卫星组网的高昂成本。
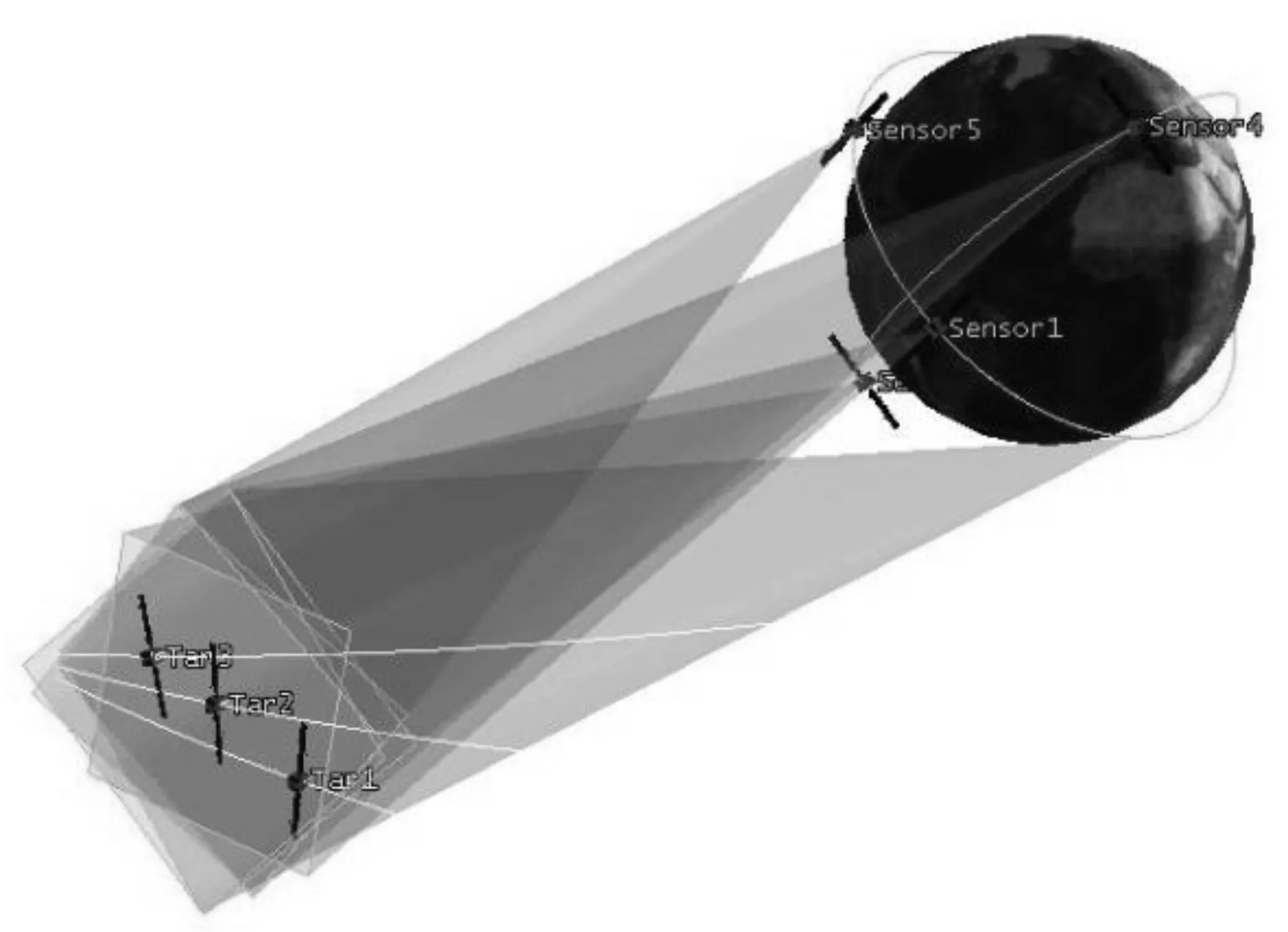
图1 多星敏感器协同观测模型
星敏感器是一种高精度的卫星姿态传感器,同时具备光学元件。根据存储的星表匹配星图中的恒星,进而确定卫星的三轴姿态,定姿精度可达1″~3″。目前星敏感器仅作为姿态传感器应用于航天器。由于星敏感器不同于专用监视卫星,其固连安装在卫星本体无法主动跟踪目标,但势必存在多颗星敏感器视场交叠的时刻。此时,视场中出现的空间目标处于多星敏感器的同步观测下,如图1所示。
文献[5]提出一种基于星敏感器的空间目标监视网络构型,并通过仿真验证了多星敏感器同步观测空间目标的可行性。文献[6]提出一种基于星敏感器仅测角数据的空间目标定轨方法,该方法的前提是对多星敏感器在相同或不同时刻拍摄的空间目标进行关联,将相同目标的测角信息用于后续计算。当前初始轨道的确定方法(比如改进拉普拉斯方法)至少需要 3 min的连续测角数据方能定出较为精确的轨道。由于太空环境的复杂性,空间目标的观测受到光照、遮挡、噪声等条件制约,将连续观测时长不足以确定空间目标初始轨道的航迹段称为短弧,其观测时长一般小于180 s。
文献[7]中提出一种自适应中值滤波方法,能够较为有效地去除星图中的椒盐噪声,并依据运动补偿算法对星图中的空间目标、噪点、恒星进行区分,提取空间目标的质心坐标。文献[8]中根据同一时刻下多星敏感器协同观测几何构型与多目视觉类似,利用对极几何原理实现空间目标的同步关联,在考虑星敏感器的抖动、测角测距误差、噪声的基础上,关联准确率可达90%。依据关联结果,通过最小二乘法来求解空间目标的坐标。文献[9]能够以改进拉普拉斯方法确定初始轨道的航迹,利用模糊关联原理实现中断航迹间的关联。文献[10]提出一种基于正弦拟合的空间目标关联方法,可区分来自不同轨道的空间目标,但是航迹间隔超过3 h时关联准确率不高,对非地球同步轨道关联效果并不好。
为解决光学测量短弧段的初始轨道估计问题,MILANI等[11]提出了容许域的概念,将空间目标按约束条件限制在由测量斜距、斜距变化率构成的二维平面内,平面中的每一点可代表一条轨道。文献[12]通过对容许域进行剖分,将其网格化,再从有限的网格节点搜索出目标初始轨道,进行目标关联。该方法有一些明显的缺陷:容许域的约束条件较为宽松,搜索初始轨道过程繁琐;在进行多对多的空间目标关联时,轨道外推环节导致算法复杂度较高,运行时间长;在噪声下空间目标关联的准确率较低[12-13]。
笔者以上述研究为基础,提出一种基于假设边值的空间目标短弧关联算法,不仅关联准确率更高,而且能适用于多种轨道类型的航迹关联。利用文献[8]中的空间目标同步关联方法及多星敏感器联合定位算法,将仅测角数据转换成观测目标的空间坐标,并假设新旧航迹关联的所有情况,从新旧航迹中各取观测点作为边值,求解假设边值条件下的目标轨道,再以马氏距离衡量假设条件下的轨道与实际观测的相似程度,最终从可能关联的阈值中选择最优关联结果。
1 基于假设边值的空间目标短弧关联算法
将间隔一定时长的航迹片段进行关联,先观测的航迹定义为旧航迹,后观测的航迹定义为新航迹。算法步骤如下:
(1) 获取m条旧航迹与n条新航迹在J2000坐标系下的位置坐标。
(2) 构造m×n的矩阵,其中元素代表以对应旧航迹一点为起点、新航迹一点为终点作为边界确定的轨道。
(3) 计算基于假设边值确定的轨道与相应新旧航迹观测值之间的马氏距离。
(4) 选择合适的阈值,小于阈值则接受关联假设,相应新旧航迹进行预关联;大于阈值则拒绝假设,相应新旧航迹不关联。
(5) 进行关联多义性处理,仅选择相似度最高的航迹组合关联,保证每条航迹最多与一条其他航迹关联。
上述步骤涉及空间目标的同步关联、多星敏感器协同定位、兰勃特定轨问题求解、基于马氏距离与卡方检验的关联判定,基本原理如下。
1.1 基于对极几何的空间目标同步关联方法
在某一时刻,两台及以上星敏感器的视线自然交汇时,相当于对重叠视野内的目标进行多角度的观测。由于空间目标距离星敏感器达数万公里,因此星图上的空间目标成像与恒星类似,为不具备细节特征的亮点。对极几何描述的是两视图内在的射影关系。当目标较远时,将目标抽象为一点,该点在两个不同视角下像的坐标存在约束关系[8]:
(1)
式(1)为对极几何约束,p1和p2代表空间目标在星图上的像素坐标,第三维补1占位。3阶方阵F称为基础矩阵:
(2)
(3)
F可根据相机标定原理求解,如式(2)所示。M1,M2分别代表星敏感器相机的内参矩阵,由式(3)求解。R,S分别代表两台星敏感器的旋转和平移矩阵。星敏感器的相机参数已知,星敏感器平台定位误差在百米内,测角误差在2″内,因此每一时刻两台星敏感器间基础矩阵可求解,每一时刻两星敏感器拍摄空间目标是否关联可判定。
式(3)中,fovx×fovy代表相机角度,Nx×Ny代表照片分辨率,f代表相机焦距,dx、dy代表像素的长度和宽度,u0、v0为主点像素坐标。上述变量均已知。
由于存在星图噪声、星敏感器抖动、测角测距误差,关联坐标代入式(1)后结果并不严格为零。设定关联阈值ε,某一时刻坐标代入式(1)后结果小于阈值的目标判定为关联。重复上述过程,最终整理出所有时刻下,所有空间目标的关联结果[8]。
1.2 多星敏感器协同定位求解
当同一时刻多星敏感器下的空间目标关联问题得到解决时,利用空间目标在同一时刻的多视角观测,根据多目视觉原理可求解空间目标的具体位置。本文空间目标的坐标在J2000坐标系中描述。J2000是经典的地心惯性坐标系,其X轴指向平春分点,Z轴指向北天极。空间目标位置的确定采用一种基于最小二乘的多星敏感器协同定位方法[8]。
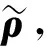
(4)
方向向量与赤经赤纬转换关系为
(5)
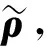
(6)
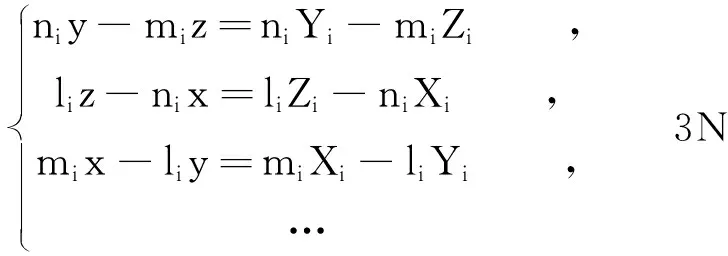
(7)
为求解未知量r(x,y,z),将其写成线性方程组的形式,为
A·X=b,
(8)
其中,
上述3N个方程中2N个相互独立。求解3个未知量,最少需两个星敏感器观测才可求解。当N>2时,其解为
X=(ATA)-1ATb。
(9)
1.3 基于假设边界的兰勃特问题求解
经上述过程,待关联空间目标的观测数据转换成了J2000坐标系下的坐标,且待关联航迹的间隔时间已知。这是一个典型的兰勃特问题,即当已知空间目标起点和终点的位置和运行时间时,可求解起点和终点的运行速度,继而求解空间目标的运动轨道[14]。BATTIN对此类问题进行了充分的研究。BATTIN法是求解兰勃特边界问题的经典解法。
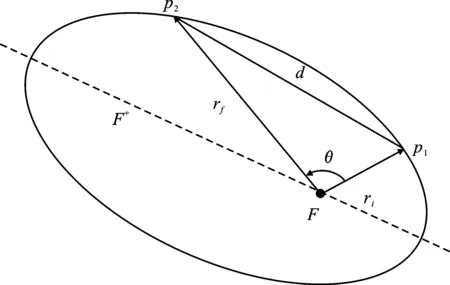
图2 兰勃特问题几何关系
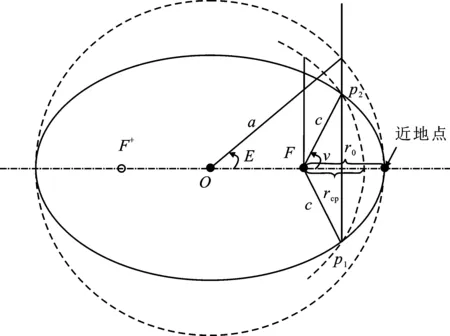
图3 兰勃特问题转换形式
由图2所示,兰勃特问题中若起始位置ri、终点位置rf确定,飞行时间是转移轨道半长轴a的函数,即
t=f(a,ri,rf) 。
(10)
根据兰勃特问题理论,若转移轨道开始和结束位置p1,p2固定,则|ri|+|rf|和半长轴在运行中不变,转移轨道初始焦点和虚焦点可以不受飞行时间约束,转移轨道形状不变。
如图3所示,转换后轨道p2点的真近点角为
(11)
其中,θ为图2中ri与rf之间的夹角。
飞行时间函数为
(12)
其中,偏心率为e;μ=398 600.44 m3/s2,代表地球引力常数。根据式(12),可推导出式(13)~(15):
(13)
(14)
(15)
可通过迭代方法求解y[15]。最终轨道起始位置的速度vi为
(16)
中间量p为
(17)
1.4 基于马氏距离与卡方检验的中断航迹关联判定
从旧航迹取一点作为起点,从新航迹取一点作为终点。若有m条旧航迹,n条新航迹,则共有mn种可能的运动情况;若旧航迹i与新航迹j属于同一目标,则在相同观测时刻,轨道上目标的理论位置必与旧航迹i和新航迹j的观测值接近,航迹的相似度利用马氏距离衡量[16]。在观测时刻k,旧航迹i和新航迹j关联理论值与观测值的马氏距离为
(18)
其中,Σ为协方差矩阵,可根据星敏感器的误差获得。
求出N个观测时刻的马氏距离,并求均值:
(19)
由于可能存在某条新航迹无法与任意一条旧航迹关联的情况,因此设置门限d。当新旧航迹平均马氏距离大于d,则判定为相应新旧航迹不关联。门限d的选取参考χ2检验法[17]。空间目标坐标为三维,应服从三自由度的卡方分布。显著性水平α=0.01,门限d=11.344。
对任一条航迹,从其满足门限d的所有候选关联航迹中选择平均马氏距离最小的航迹判定为关联,并保证每条航迹至多有一条关联航迹。
2 仿真校验
2.1 多星敏感器协同定位精度仿真
利用卫星工具包(Satellite Tool Kit,STK)平台构建观测模型。观测平台位于太阳同步轨道,轨道参数参考美国优思科学家联盟的观测数据。观测平台的轨道倾角范围为96.8°~98.5°,轨道半长轴为6 778.14 km,偏心率为0,每个平台正交安装两台视场为2°×2°的星敏感器。观测目标位于轨道半长轴为42 126.1~42 805.9 km的地球同步轨道,轨道倾角为0°~2°。共进行了200次地球同步轨道目标的协同定位,计算了空间目标定位坐标与实际坐标的误差。为模拟任务中星敏感器定姿误差及平台自身的位置误差,对测角、测距数据加入噪声。仿真中设置了3种噪声水平,(a″,b)意味着对星敏感器的测角数据加入均值为零、标准差为a″的高斯白噪声,对星敏感器的位置矢量加入均值为零、标准差为b的高斯白噪声。图4反映了200次计算中空间目标在X,Y,Z轴的定位误差情况。
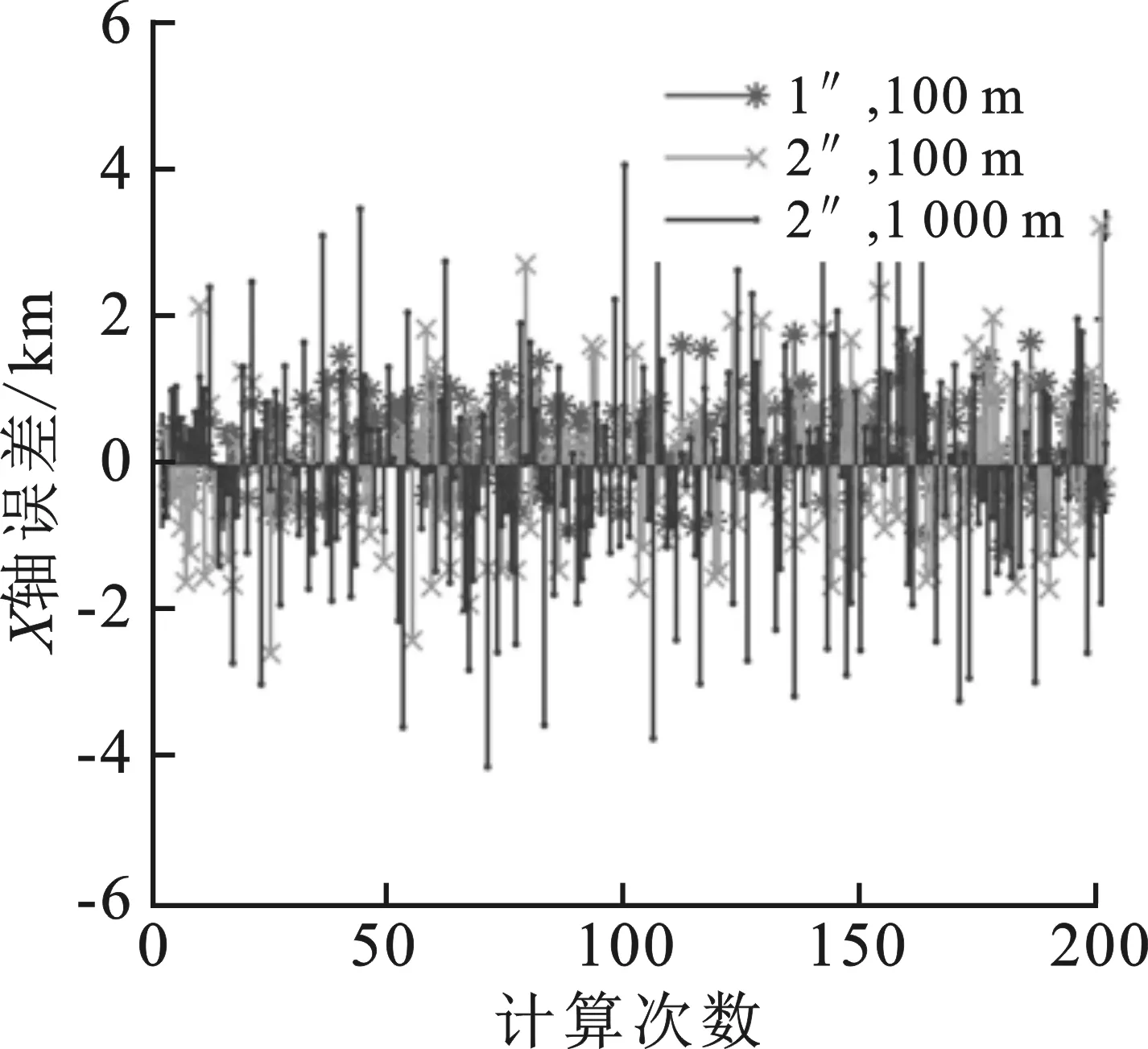
(a) X轴误差
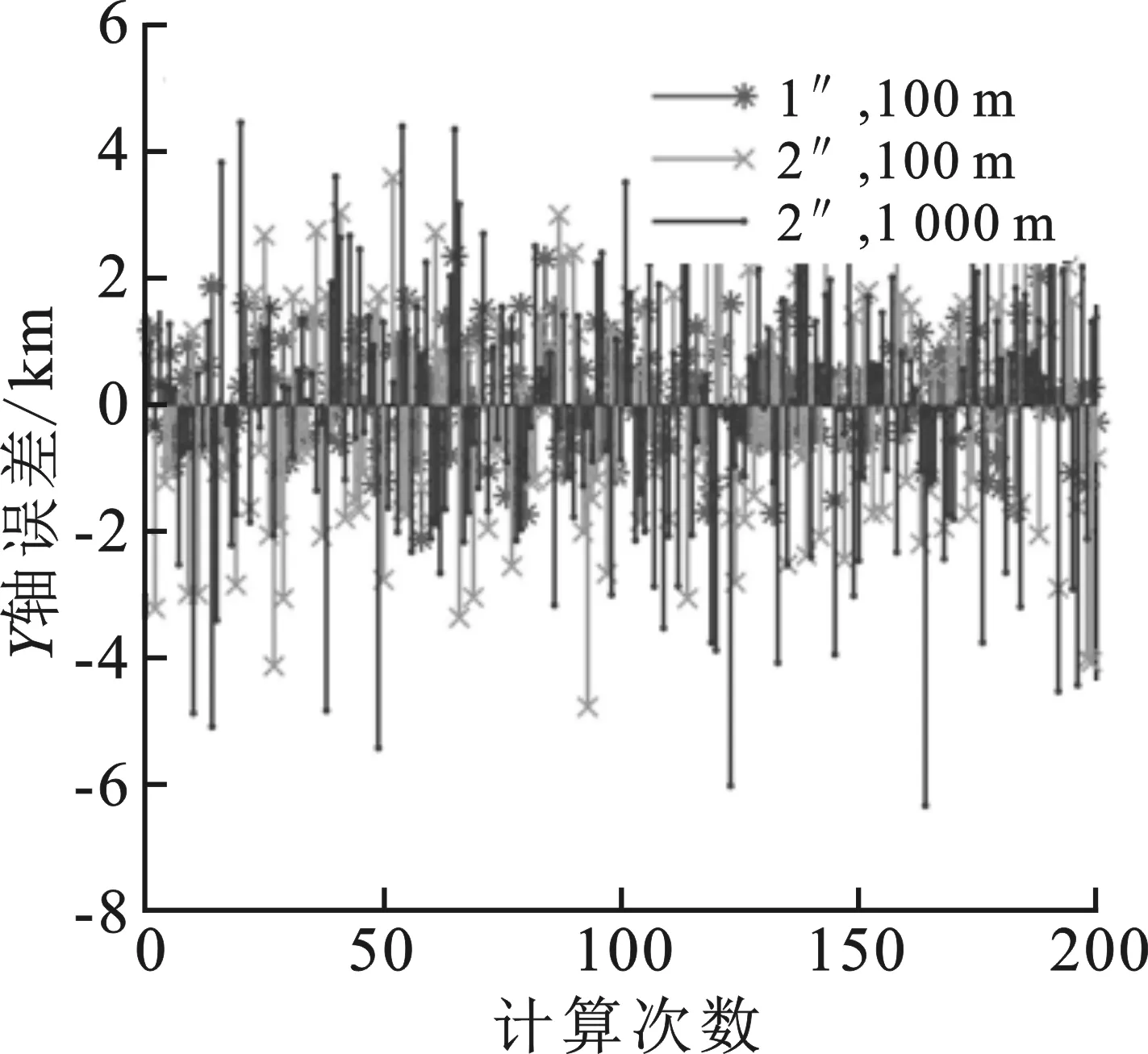
(b) Y轴误差

(c) Z轴误差
三轴定位误差的标准差如表1所示。当噪声(1″,100 m)增大到(2″,100 m)时,定位误差改变了0.922 3 km;当噪声(2″,100 m)时增大到(2″,1 000 m)时,定位误差仅改变了0.794 4 km。测角误差多1″,就会对定位结果产生明显的影响。可见协同定位算法对测角误差更为敏感。星敏感器测角越准,定位精度越高,后续关联效果将越好。

表1 三轴定位误差的标准差
2.2 空间目标短弧关联仿真
采用实测数据与仿真相结合的研究方法,将真实的地球同步轨道数据导入卫星工具包。轨道半长轴为42 126.1~42 805.9 km,轨道倾角为0°~2°。图5为2019年12月1日0时在轨533个地球同步轨道目标在J2000坐标系下的分布密度图,纵轴代表1°×1°区域内空间目标个数。可知目标在中国、俄罗斯、美国的上空较为密集。据统计,大多数地球同步轨道目标分布的赤道纬度接近于0°,且都为近圆轨道,最大偏心率为0.075,其中80%目标的轨道倾角小于1°。
仿真中观测平台建立在倾角范围为96.8°~98.5°、轨道半长轴为6778.14 km、偏心率为0的30个太阳同步轨道上,每个平台正交安装两台视场为2°×2°的星敏感器,组成空间目标监视网。利用卫星工具包平台获取连续时刻及对应时刻坐标作为航迹数据。根据节2.1的结果对航迹坐标添加噪声,每组噪声下共进行了500次的关联仿真。定义观测时长180 s以下的弧段为短弧。为着重突出短弧关联效果,选择观测时长为50~120 s的航迹数据进行关联。一般空间目标的重访时间为20~50 min,可关联的航迹间隔时间越长,数据的利用率越高。仿真中最大间隔时间为10 h,可满足绝大部分的中断航迹关联需求。在双核Intel 2.5 GHz的MacBook pro上,采用Matlab2018a版本进行航迹关联仿真。
关联性能由真正类(True Positive,TP)、真负类(True Negative,TN)、假正类(False Positive,FP)、假负类(False Negative,FN)4个量来描述,TP指正确关联相同目标,TN指正确拒绝不同目标,FP为误关联不同目标,FN指漏关联相同目标。图6所示为基于假设边值的关联算法在不同噪声条件下的关联正确率。随着间隔时间增加,关联准确率呈下降趋势。根据现有星敏感器的性能,测角误差为2″、位置误差为100 m的噪声更符合工程应用实际。参考三角记号折线,航迹间隔10 h,关联准确率达95%。表2展示了在此噪声条件下,不同间隔时间下的具体关联结果。
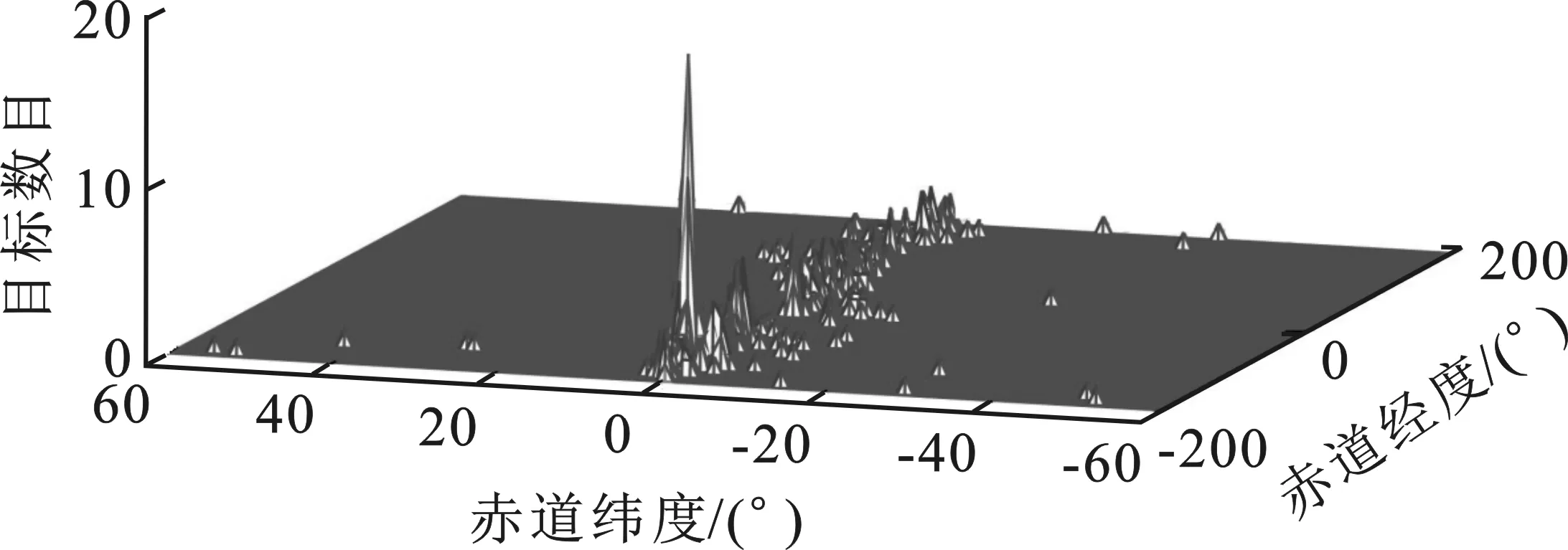
图5 地球同步转道目标分布密度图
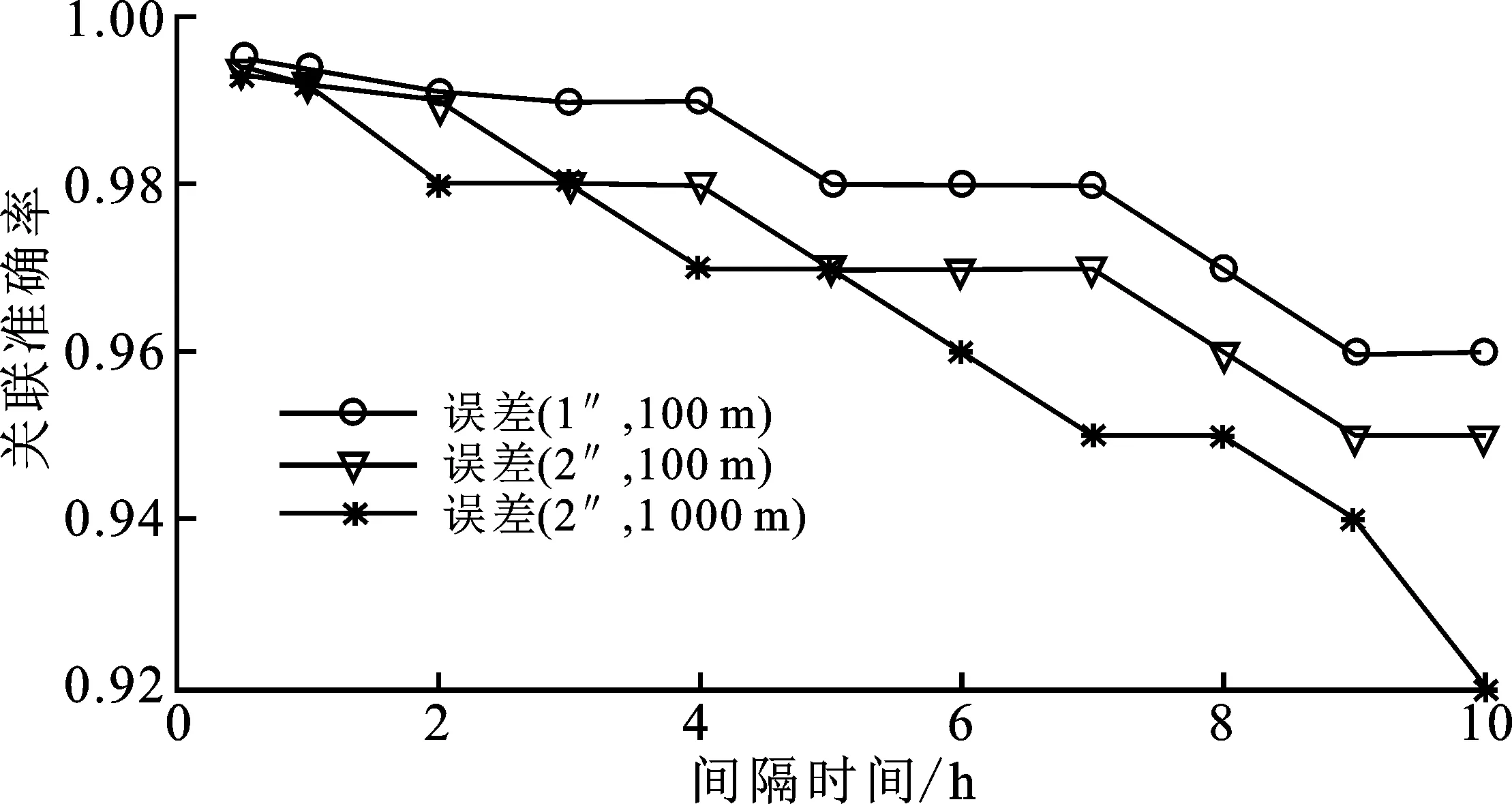
图6 关联准确率与间隔时间的关系
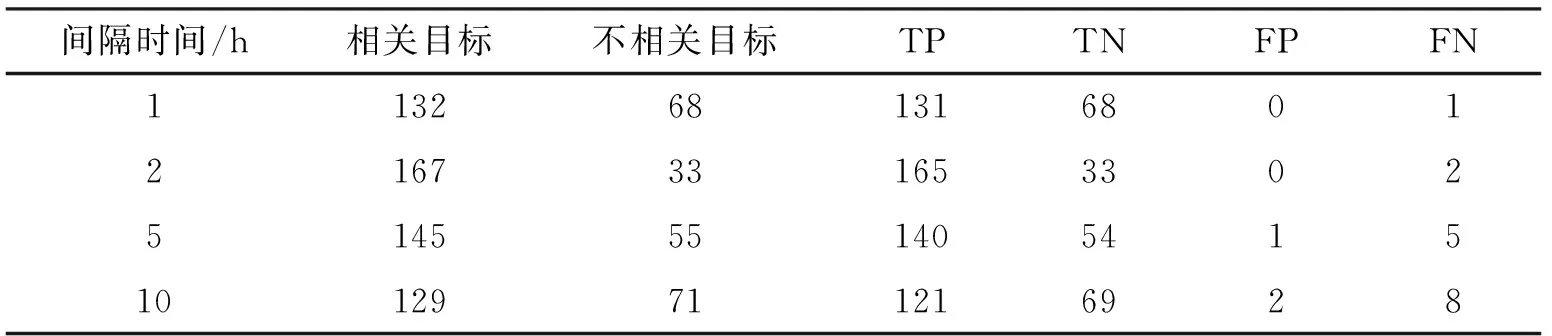
表2 关联结果统计
仿真中的关联门限值d取11.344。若新旧航迹平均马氏距离大于d,则判定为不相关航迹。门限值与关联同一目标的概率有关[18]。门限值取得过小,会将同一目标拒绝,造成漏关联;门限值取得过大,则可能将不同的目标误判为关联。关联同一目标概率随门限取值变化如图7所示,曲线先增大后缓慢减小。由于来自于同一目标观测数据与预测数据的马氏距离往往比来自不同目标的马氏距离小,因此达到最大关联概率后的下降趋势相较于上升趋势平缓得多。
图8为目标关联的可视化展示。图中3个方块代表3个观测时刻,依次间隔为1 h,观测目标为地球同步轨道目标,成功关联的目标用相同标记表示,可知共有4个地球同步轨道目标。地球同步轨道目标绕地心运动的角速度约15°/h,与图8中地球同步轨道运动状态相吻合。
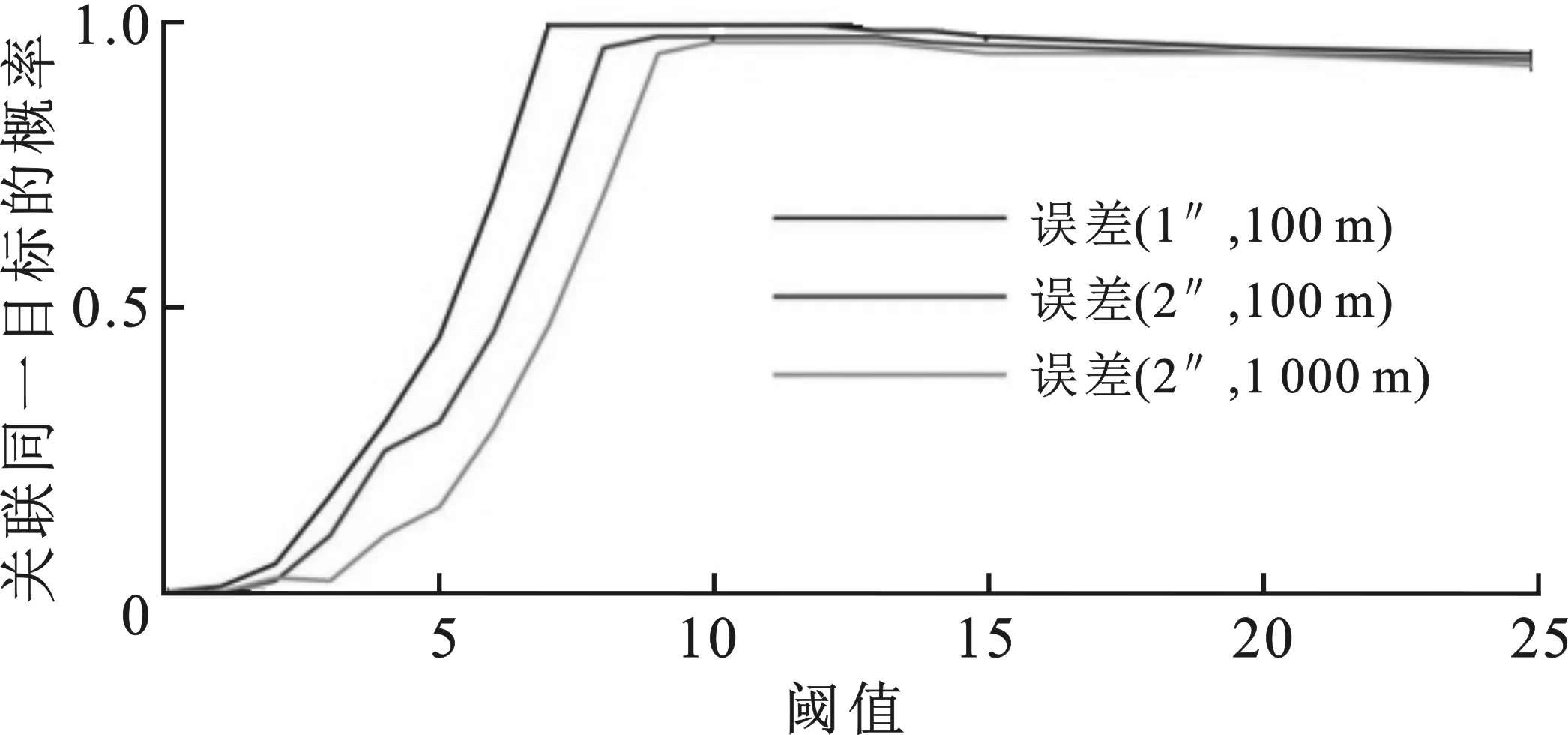
图7 关联概率与阈值的关系

图8 关联结果示例
3 短弧关联算法对比
为测试基于假设边值的航迹关联算法解决短弧关联问题的性能,通过仿真从关联准确率、运行时间两个角度,与基于正弦拟合和基于容许域的短弧关联算法进行对比。容许域算法通过将目标的轨道限制在测量斜距与斜距变化率的平面的一定范围内,以寻找和观测值误差最小的轨道作为初轨,根据目标的半长轴、轨道倾角等特点可以进一步缩小约束范围。基于正弦拟合的关联算法利用同一轨道的赤道经纬度的变化,近似正弦分布的规律,区分轨道倾角不同的轨道。仿真中添加噪声为(2″,100 m)的高斯白噪声,仿真中的关联阈值d取11.344。3种算法分别对不同间隔时间进行100次仿真,统计关联准确率如图9所示,并在上述仿真过程中对5、10、30、60个目标同时关联的平均运行时间进行计算,如图10所示。
基于假设边值的短弧关联算法与基于正弦拟合的短弧关联算法[10]利用了多星敏感器同步关联结果,融合了多星敏感器的同步观测数据,而容许域方法针对单平台仅测角数据,因此基于容许域方法的关联准确率最低,且容许域约束相对宽松。基于容许域方法对每个观测目标都需要在容许域内寻找最优初轨,再外推到下一时刻与后一时刻的目标进行关联,过程复杂,关联时间也是最长的。基于正弦拟合的空间目标关联算法[10]可以较为便捷地区分倾角不同的轨道,对于同轨道不同相位或仅轨道高度不同的空间目标需增加额外约束条件,因此难以适应多种轨道类型的目标关联,并且随关联间隔时间增加,关联准确率下降明显;由于无须进行轨道确定及轨道外推,运算最快。基于假设边值关联算法的运算时间略高于基于正弦拟合关联算法,但关联准确率在3种算法中最高;从仿真结果看,当航迹间隔在10 h内时,进行关联的准确率均比较高。

图9 准确率的对比

图10 运行时间对比
4 结 论
在多星敏感器观测的空间目标同步关联结果基础上,使用最小二乘方法将相同时刻多星敏感器观测的测角数据融合,解算出各空间目标在J2000坐标系下的坐标。当星敏感器位置误差的标准差为100 m、测角数据误差的标准差为2″时,空间目标定位误差的标准差为1.977 1 km,足以满足后续关联步骤的精度需求。基于假设边值和基于正弦拟合关联算法的应用前提是需至少两台星敏感器对空间目标进行观测,根据文献[5]相关研究,90%同步轨道带目标可被两台以上星敏感器同步观测。
从新旧航迹中各取一点作为边界,建立所有假设边界的集合,计算出所有假设边界条件下空间目标轨道的理论值,并利用马氏距离与卡方检验作为航迹关联准则。经仿真验证,当噪声为(2″,100 m)的高斯白噪声时,对两组间隔10 h航迹关联的准确率可达95%。与其他短弧关联算法相比,基于假设边值的航迹关联算法在关联准确率上具有明显优势,同时保持了较快的运行速度。
仿真中采用的最短观测仅50 s,无法用常规轨道确定方法确定初始轨道,符合短弧定义。基于假设边值的航迹关联算法实现了因观测弧段过短无法确定初轨的航迹关联问题,而且算法不仅局限于短弧关联,对一般的航迹关联问题同样适用。若未来星间链路能够实现卫星间数据共享,则空间目标关联的过程可在卫星上实现,无需再将大量数据下传回地面。由于卫星的运算资源是有限的,因此算法不宜过于复杂。在3种短弧关联算法中,基于假设边值的航迹关联算法更有利于实现星上数据处理。
考虑到各平台的实际测量误差可能有所不同,后续将对不同平台的观测误差赋予相应的权重,进一步提高空间目标的定位精度。目前,工程中星敏感器仅作为姿态传感器应用,通过实测数据与仿真软件相结合的手段,可为后续工程应用提供借鉴。随着新型小视场、高极限星等星敏感器的研发,后续将在真实星图下进一步进行空间目标提取研究。
