同轴电缆感性脉冲电流注入试验仿真方法

崔志同，魏 兵，吴 伟，孙蓓云

(1.西北核技术研究所 强脉冲辐射模拟与效应国家重点实验室，陕西 西安 710024；2.西安电子科技大学 物理与光电工程学院，陕西 西安 710071)

自然或人为(雷电、开关操作、高空核爆等)产生的强电磁脉冲可在电子设备的连接电缆上耦合强瞬态电磁干扰，进而影响电子设备的正常工作，甚至导致其损伤失效[1]。为评估电子设备的强电磁脉冲易损性，通常采用电磁场辐照或者传导试验的方法[2]。其中，感性脉冲电流注入(Pulsed Current Injection，PCI)是一种常用的传导试验方法，是GJB151B和GJB8848—2016等标准推荐的测试方法。感性脉冲电流注入基于磁芯变压器的能量耦合原理，可在不破坏被试对象连接线缆物理结构的情况下，在设备端口施加强瞬态电流信号以考核其抗电磁干扰能力。另外，该方法还具有成本低、操作便利、可在设备研制早期介入等优点，因此在电子设备强瞬态电磁效应研究中得到了广泛应用[3]。

为深入理解感性脉冲电流注入的物理过程，量化分析脉冲电流注入试验平台中各参数变化的影响，文献[3-5]开展了感性脉冲电流注入的电路建模分析工作，并在此基础上给出了一种实现注入与辐照等效的工程实现方法。但这些工作主要针对非屏蔽线缆，而未涉及在实际设备中广泛应用的屏蔽电缆。因此文中拟以同轴电缆为例，开展针对屏蔽电缆的感性脉冲电流注入仿真研究工作。

目前在电磁兼容领域的电流注入(Bulk Current Injection，BCI)研究工作中，考虑了被试线缆为屏蔽电缆的建模仿真问题[6-8]，如文献[6]在已知电缆屏蔽层注入点处电流的情况下，给出了屏蔽层与芯线间耦合的Spice电路模型，用于仿真芯线电流。但这些工作以频域仿真为主，对时域情况关注较少，同时试验平台的整体建模技术研究也有所欠缺(如未将激励源实际电路纳入到模型当中)；另外，其转移阻抗使用简化的理论模型且未考虑散射电感为负值的问题。这些都可能导致此类模型在时域的全平台仿真时存在不收敛及精度偏低等问题。

针对上述需求及问题，笔者将首先分析同轴电缆感性脉冲电流注入试验的作用机理，并介绍相关的研究基础，给出由脉冲电流注入确定的边界条件下，转移阻抗适用的测试方法以及屏蔽层与芯线间耦合关系的计算方程，建立一种Spice+Matlab联合仿真方法；另外，着重解决转移阻抗实测值的电路拟合建模以及屏蔽层与芯线耦合的Spice电路建模问题，以建立同轴电缆感性脉冲电流注入的全Spice电路模型仿真方法。

1 同轴电缆感性PCI的基本设置及其作用机理

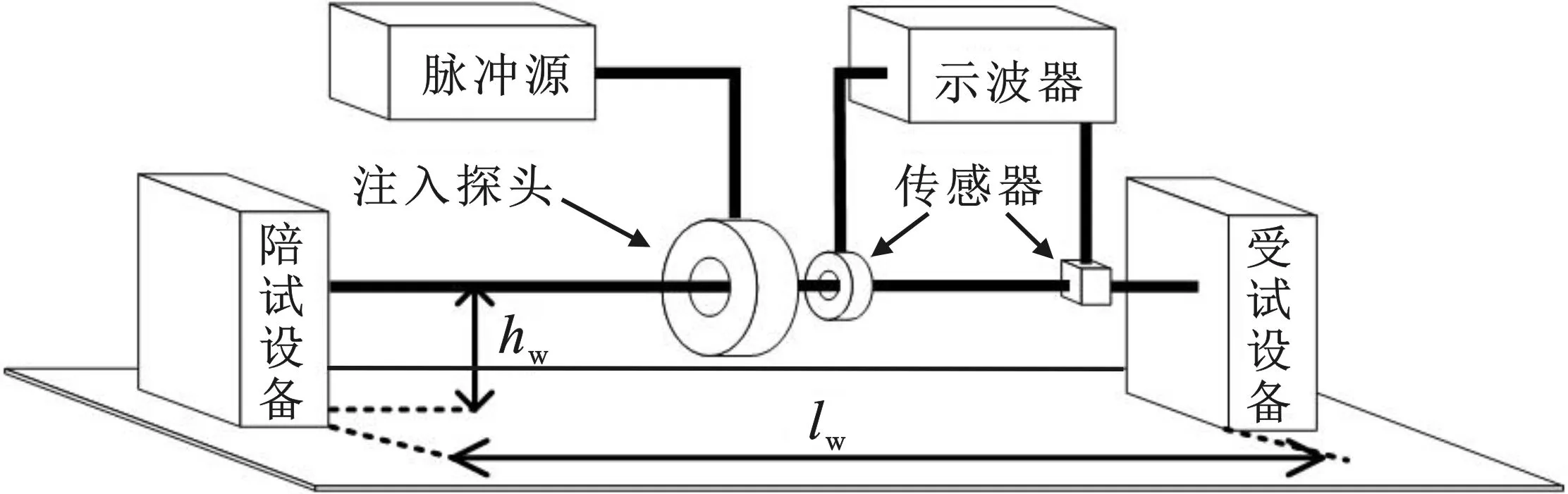
图1 同轴电缆感性PCI试验的基本设置示意图

同轴电缆感性脉冲电流注入试验的基本设置如图1所示。主要包括脉冲源、电流注入环、受试设备、陪试设备及两者间连接电缆；另外还包括配套的电流测试系统，即电流传感器和数据采集记录设备。其中，电流注入环为基于铁氧体磁芯的感性耦合装置，工作原理与变压器一致[9]。测试系统中，邻近注入环的传感器用于测量电缆屏蔽层电流，右侧的通过式传感器用于测量电缆芯线耦合电流。

感性脉冲电流注入的电磁干扰加载过程可以分为两步：首先，电流注入环将脉冲源输出能量耦合到电缆屏蔽层上，可视为在注入点处形成一个串联的集总电流源，其电流在屏蔽层与地组成的外部传输线上传播；之后，屏蔽层电流通过转移阻抗Zt将能量耦合到电缆芯线上，进而在受试设备端口产生电磁干扰。需要说明的是，在同轴电缆感性脉冲电流注入试验中，屏蔽层左右两侧末端均接地，因此转移导纳Yt的作用可以忽略；另外，基于电缆的良好屏蔽假设[10]，芯线通过屏蔽层耦合到外部的能量在这里也未予考虑。

与作用机理相对应，同轴电缆感性脉冲电流注入的仿真可分为两个部分：对于脉冲源到屏蔽层的电流耦合，可以使用Spice电路建模的方法，这便于建立包含脉冲源实际内部电路的脉冲电流注入完整模型；对于电缆屏蔽层到芯线的耦合，可以选择利用Matlab进行解析计算或者Spice电路建模的方式。考虑到电子设备面临的主要强瞬态电磁传导环境，以及感性脉冲电流注入的适用范围，在仿真研究过程中，以100 MHz为脉冲频率范围上限[11]。

2 同轴电缆感性PCI仿真研究基础

2.1 电缆屏蔽层PCI的Spice电路仿真

将电缆屏蔽层视为对地传输单线，按照文献[4]所述方法建立如图2所示的电路模型，即可仿真得到屏蔽层在脉冲电流注入试验中的耦合电流。该模型主要包括脉冲电流源、电流注入环、被试线缆及负载，以及环电路与被试线缆及负载间的耦合电路。其中，脉冲源通常采取方波、双指数波及衰减振荡波等形式；电流注入环采用基于电阻电感电容(RLC)网络的时域集总参数等效电路模型，各参数值通过对注入环端口阻抗测试结果的拟合来求解；被试线缆使用Spice的无损传输线模型进行表征，线缆末端负载RL、RR可设为1 mΩ(近似于良好接地)。

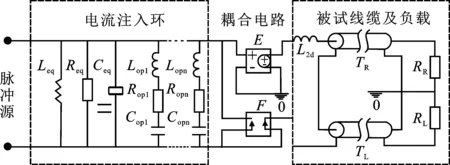
图2 电缆屏蔽层感性PCI电路模型

图3 双指数波脉冲源电路模型

以RLC回路构成的双指数波脉冲源为例开展研究工作，其工作原理和电路模型如图3所示，主要包括了充电回路和放电回路两部分。脉冲源工作时，开关SW首先掷向左侧，将充电回路导通，高压直流源VDC通过充电电阻Rc给主电容C0充电；之后，开关SW切换至由C0、内阻R0以及杂散电感L0构成的放电回路一侧，并经电缆T0传输至负载ZLS形成脉冲输出。

2.2 转移阻抗的获取方法

转移阻抗是电缆屏蔽层和芯线耦合的关键参数。由于电缆屏蔽层编织网的非均匀性，以及外部电磁场耦合到芯线的复杂性，使电缆转移阻抗的建模通常比较困难。测量是获取转移阻抗最为可靠的方法[10]。常用的转移阻抗测试方法包括三同轴法、线注入法、电流探针法等。其中，三同轴法中的短路-短路法操作相对快速、简便，且适用频率范围能够满足感性脉冲电流注入仿真需求[12-14]。

短路-短路测试法的基本原理如图4所示。选取一定长度的电缆样品，在其外绝缘皮上再套一层编织网；将被测电缆左侧芯线与屏蔽层相连，同时以外套屏蔽层为参考地，连接至矢量网络分析仪的端口1(Port 1)；将右侧屏蔽层与外套屏蔽层相连并作为参考地，将其与芯线连接至矢网的端口2(Port 2)。根据测试得到的S21参数推导电缆单位长度转移阻抗的计算方程[13]可表示为

Zt=RvS21/lc，

(1)

其中，Rv为矢量网络分析仪内阻，lc为被试线缆长度。

对于电缆测试样品尺寸，一方面应满足电小条件；另一方面也需考虑尺寸问题，尺寸越小，由连接头等带来的测量误差越大。基于上述因素，可以按照lc=10 cm进行样品制备，该长度满足以100 MHz为频率上限的同轴电缆脉冲电流注入仿真需求(lc≪c/f，c为光速，f为上限频率)。

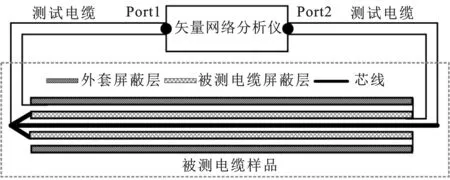
图4 转移阻抗短路-短路测试方法示意图

2.3 电缆屏蔽层与芯线间的耦合

与转移阻抗一致，电缆屏蔽层耦合到芯线间的耦合电流也采用频域形式进行求解和表征[15]。

(1) 计算电缆屏蔽层上的分布电流Iout。设定在以电缆左侧为0点的位置坐标中(自左至右为x正向)，注入点x位于d处，电缆长度为lw。脉冲源通过注入环在注入点处形成的电流为Iinj。屏蔽层两侧末端接地。则注入点左侧Iout=IL时，可用下式表示：

(2)

在注入点右侧Iout=IR时，可用下式表示：

(3)

其中，β0为屏蔽层与地组成传输线的传播常数，β0=2πf/c。

(2) 计算屏蔽层电流在芯线上产生的分布激励源。由于忽略了转移导纳的影响，只需考虑转移阻抗Zt形成的电压源，即

VTin(x)=ZtIout(x) 。

(4)

(3) 求解电缆芯线的终端响应。按照传输线方程，芯线的终端响应可表示为

(5)

(6)

其中，Zcin为电缆的特征阻抗；βin为芯线与屏蔽层组成传输线的传播常数，可表示为

βin=2πfεr1/2/c，

(7)

其中，εr为电缆绝缘层的相对介电常数。

在芯线末端负载RL、RR已知的情况下，便可建立Vin(0)和Iin(0)、Vin(lw)和Iin(lw)间的关系：

(8)

(9)

最后利用式(2)～(9)，即可求得注入点电流Iinj耦合到芯线末端负载的频域电压Vin、电流Iin。

3 Spice+Matlab联合仿真方法

依据同轴电缆感性脉冲电流注入的作用机理，可以采用Spice+Matlab程序对其进行建模仿真。使用Spice仿真得到电缆屏蔽层电流，再利用Matlab计算得到芯线末端耦合电流、电压。具体仿真过程如图5所示。

图5 Spice+Matlab程序联合仿真方法

首先将电缆屏蔽层视为传输单线，利用脉冲电流注入的基本电路模型(如图2所示)仿真得到其屏蔽层电流I(t)，通过傅里叶变换得到对应的频域电流Iout；通过实验测试获取电缆转移阻抗Zt，并将Iout、Zt的频点进行处理以使其一致；然后利用式(2)～(4)计算得到转移阻抗在芯线上形成的电压源VTin；之后利用芯线与屏蔽层间的传输线方程式(5)～(9)计算出芯线末端频域耦合电压Vin；最后在对频域数据进行滤波等数据处理后，进行傅里叶逆变换，得到芯线耦合电压的时域值V(t)。

4 全Spice电路仿真方法

Spice+Matlab联合仿真的方法在求解电缆屏蔽层与芯线间耦合时采用了频域方程，因此不便于处理受试设备端口为非线性或时变负载的情况。为此，研究了同轴电缆感性脉冲电流注入的全Spice电路仿真方法，主要实现途径为：在电缆屏蔽层脉冲电流注入电路模型的基础上，进一步建立转移阻抗的拟合电路模型、屏蔽层与芯线间耦合的集总近似电路模型，形成一种全Spice电路仿真模型。

4.1 转移阻抗的等效电路模型

目前同轴电缆转移阻抗的电路表征方法主要基于其常用的理论计算模型(Zt=Rdc+jωLt)，采用电阻与电感串联的形式[10，15]。这一方法存在的主要问题有两个：一是在电缆屏蔽层编制角小于45°时，编织网孔电感为负值，在Spice电路中不能直接用电感表示；二是实测的转移阻抗往往较为复杂，难以用简单的电阻与电感串联模型进行表征，无法在电路模型中有效地使用测试数据以提高仿真精度。

对于转移阻抗存在负值电感的问题，可以应用电路响应等效原理解决。如图6(a)所示，通过电压控制电压源和电流控制电流源的转换作用，右侧端口的电压值与电感Ln上的电压值大小相等，方向相同；电流值与电感Ln上的电流值大小相等，方向相反。因此从右侧端口看，该电路模型相当于一个负值电感-Ln。

对于转移阻抗实测数据的电路拟合问题，可通过在基本模型基础上增加优化电路的方法来解决。根据转移阻抗的特性，优化可分别针对转移电感、基本模型进行，即并联优化电路ZL_op和Zt_op，如图6(b)所示。与电流注入环的优化电路模型相似，ZL_op和Zt_op可采用RLC串联电路的方法，其中若涉及到负值电阻或电容，其处理方式与负值电感电路一致。需要注意的是，在采用多级优化电路以提高拟合精度的同时，也应避免出现因电路复杂度提高而导致的仿真收敛性问题。

(a) 负值电感模型

(b) 转移阻抗拟合模型

4.2 屏蔽层与芯线耦合的集总近似电路模型

按照传输线的集总近似原理[16]，将电缆分为若干满足电小条件的线段，每段屏蔽层电流通过转移阻抗在芯线上形成一个电压源，再将各线段串联之后便可建立起芯线末端耦合电压的电路仿真模型。该模型在Spice中的具体实现方式为：首先，将受试电缆屏蔽层与地构成的传输线分为n段，并利用电流控制电压源提取各段间的电流In，如图7(a)所示，其中注入点位于第m段和m+1段之间；之后，利用电压控制电流源GVALUE和电压控制电压源EVALUE，构建转移阻抗在对应各段芯线上形成的电压源，其值设为InZt_eqlw/n；最后，将该电压源加入芯线与屏蔽层传输线的分段模型中，如图7(b)所示。与电缆转移阻抗测试样品长度一致，屏蔽层与芯线耦合的集总近似电路也可按10 cm长度进行分段，对应的频率上限大于 100 MHz，能够满足感性脉冲电流注入仿真需求。

将图3所示脉冲源电路、图2所示电流注入环初级与次级耦合电路部分、图7所示屏蔽层与芯线间耦合电路进行整合，即可得到同轴电缆感性脉冲电流注入的全Spice电路模型。

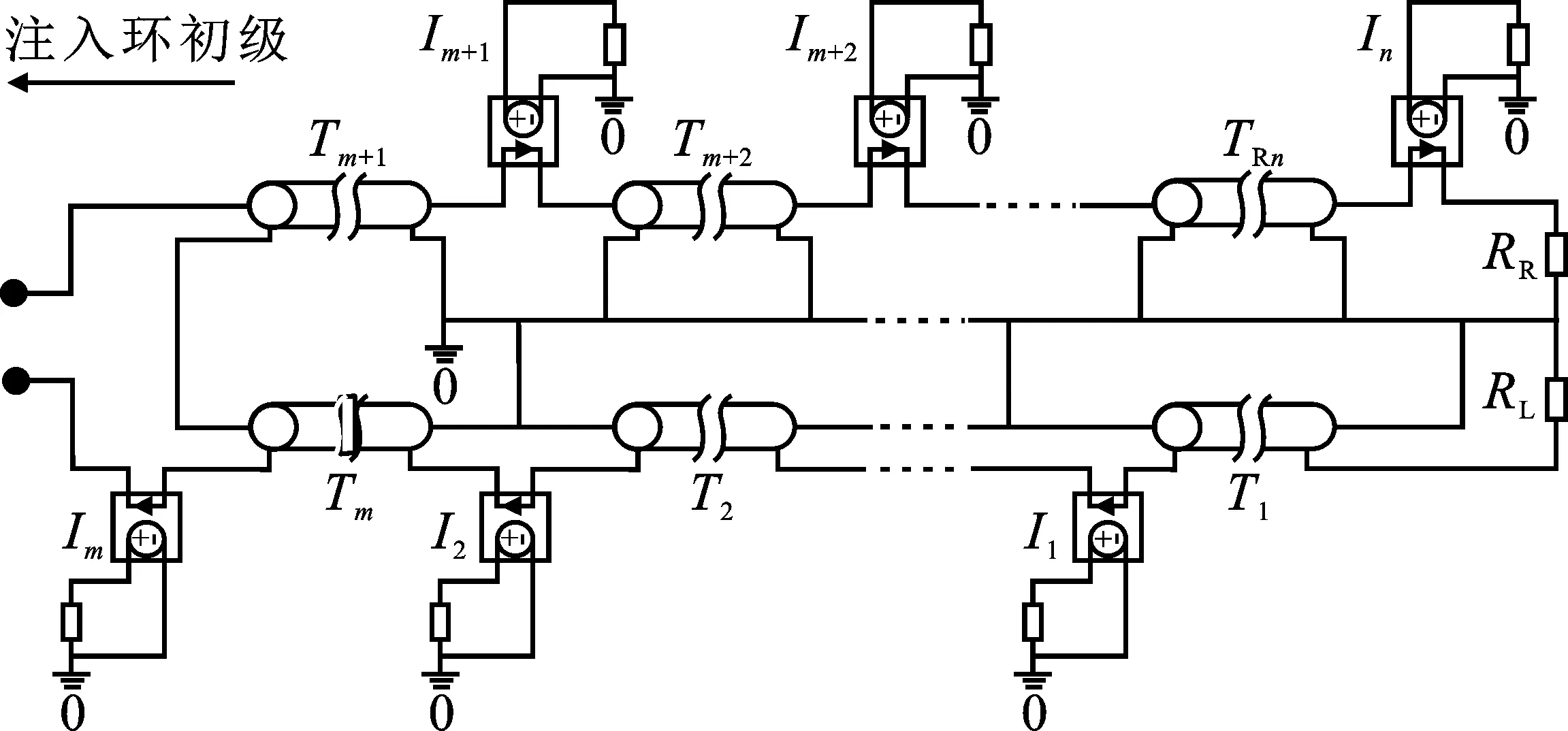
(a) 屏蔽层-地传输线模型

(b) 屏蔽层-芯线耦合模型

5 仿真方法验证

针对上述两种方法开展数值和实验验证，基本设置为：① 脉冲源输出为双指数波，电路模型如图3所示，放电回路参数C0=5.6 nF，R0=50 Ω，L0≈0.15 μH；② 被试同轴电缆型号为RG 58，长度lw=0.6 m，架高hw=67.5 mm，注入环位于线缆中点，对应图2模型中无损传输线TR、TL的特征阻抗Zcout=257 Ω，延迟时间τcout=1.15 ns，芯线末端负载RinL=RinR=50 Ω；③ 电流注入环为FCC生产的F-120-6型，标称带宽10 kHz～400 MHz，对应图2模型中电流注入环模型参数[4]Leq=40 μH，Req=280 Ω，Ceq=5.5 pF；Rop1～6=80、350、500、650、2 800、30 Ω，Lop1～6=80、80、40、10、6、0 μH，Cop1～6=109、4.2、1、1、1、9×10-3nF；④ 按照图4所示设置制备和测量被试电缆的转移阻抗，并按图6所示模型对测量结果进行拟合(试错法)，得到模型各参数值，其中Rdc=12.5 mΩ，Lt=-2.5 nH，ZL_op由-40 mΩ电阻和-0.7 nH电感串联而成，Zt_op由-0.4 Ω电阻和0.25 nH电感串联而成；⑤ 在屏蔽层与芯线耦合的集总近似电路模型中，每段传输线长度为10 cm，Tn延迟时间为0.33 ns，Tinn延迟时间为0.5 ns；⑥ 配套测试设备，电流测试传感器为Person公司产品，屏蔽层电流传感器型号为8585 C，带宽为1.5 kHz～200 MHz；芯线电流传感器型号为6027，带宽为1 kHz～250 MHz。

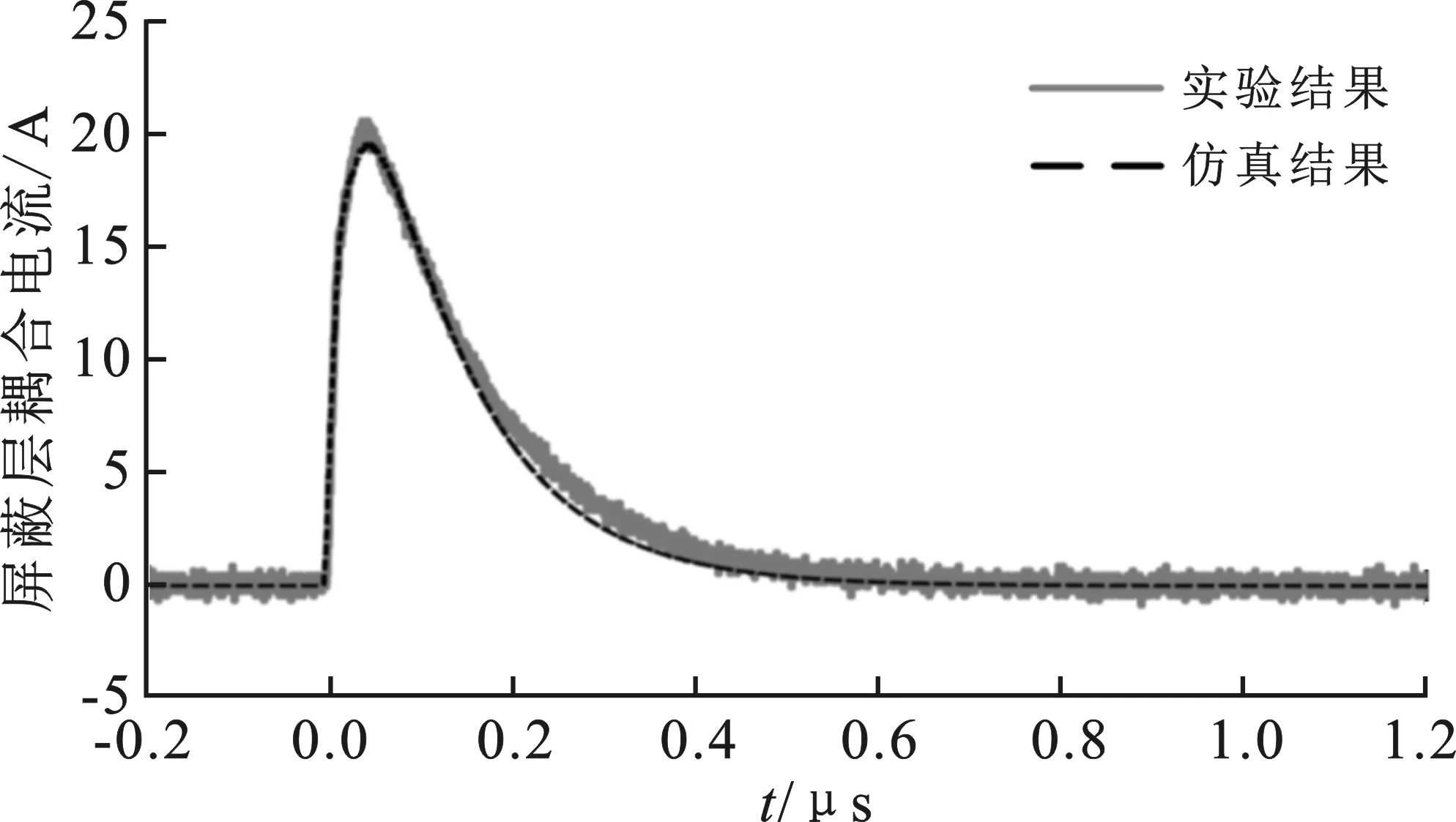
图8 电缆屏蔽层耦合电流的仿真与实验结果

首先，对电缆屏蔽层耦合电流电路模型(图2、图3)进行验证。在脉冲源加压1 kV的条件下，屏蔽层耦合电流的实验与仿真实验结果对比如图8所示，可见两者具有较好的一致性。

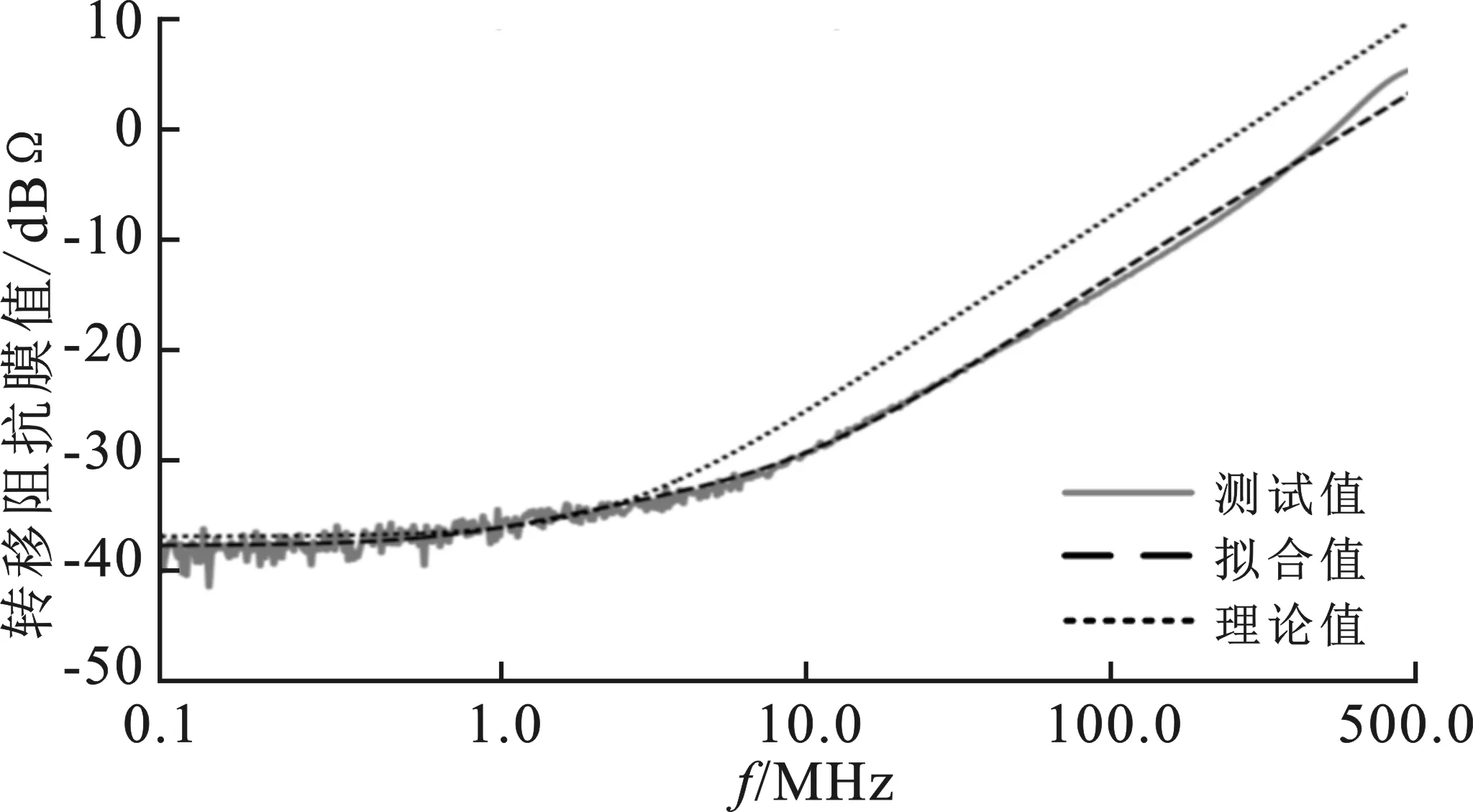
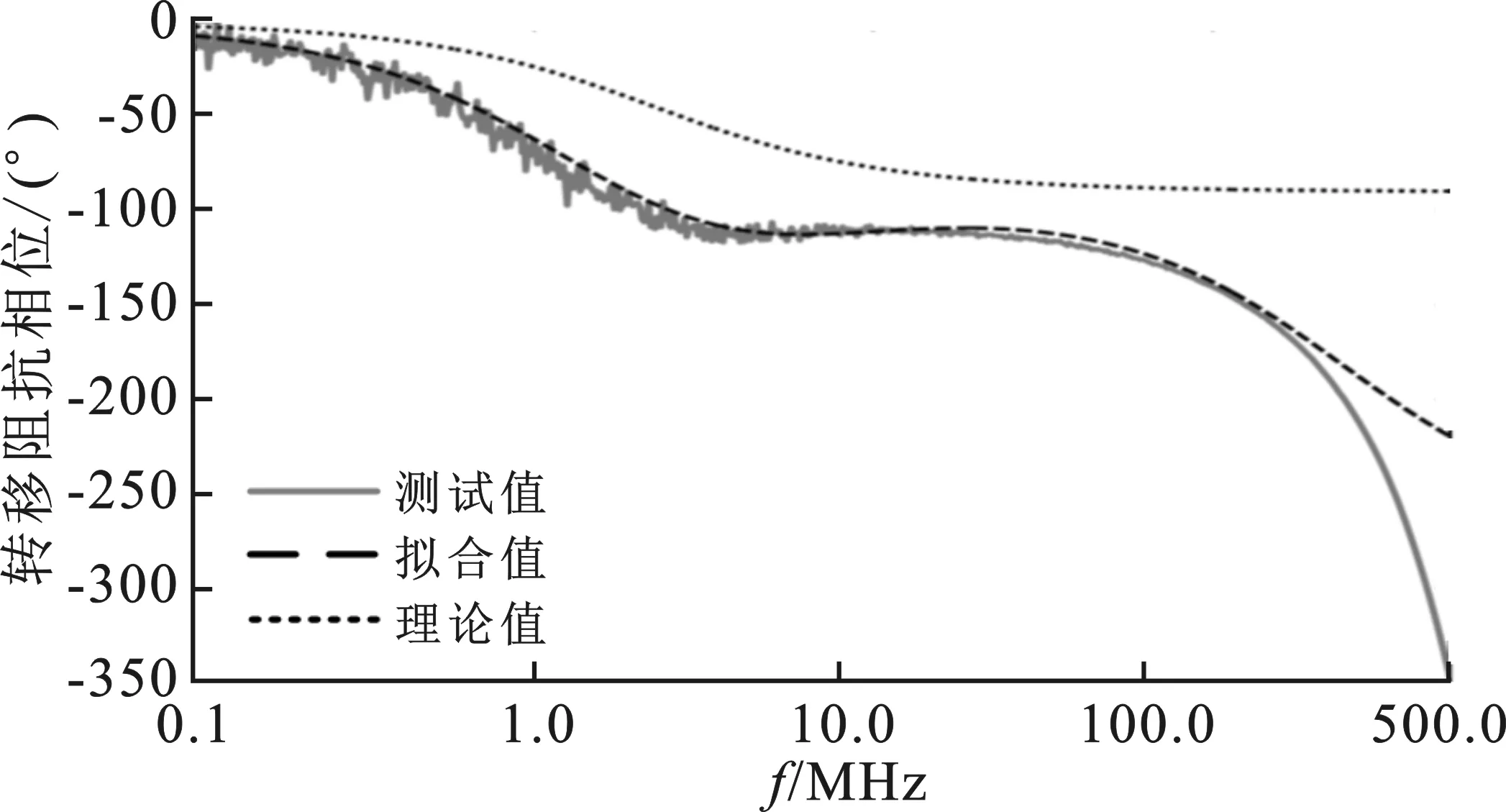
其次，对转移阻抗的等效电路模型(图6)进行验证。电缆转移阻抗的理论值、测试结果、电路拟合值比对如图9所示，其中理论值Zt=14.2 mΩ-1 nH。可见，无论从幅度上还是从相位上看，理论值与实测值都存在较大的差异；而拟合值则与测试值具有较好的一致性，从而表明了转移阻抗电路拟合模型的必要性和可行性。

再次，对屏蔽层与芯线耦合的集总近似电路模型进行验证。在其Spice电路模型(图7)中，在屏蔽层注入位置加载幅度为1 A的交流激励源IAC作为输入，芯线末端负载RinR上的耦合电压作为输出，两者的比值定义为该模型的传输函数。按照式(2)～(9)计算得到的解析结果，与集总近似电路模型的仿真结果对比如图10所示，两者在100 MHz以下符合较好。

(a) 幅度比对

(b) 相位比对

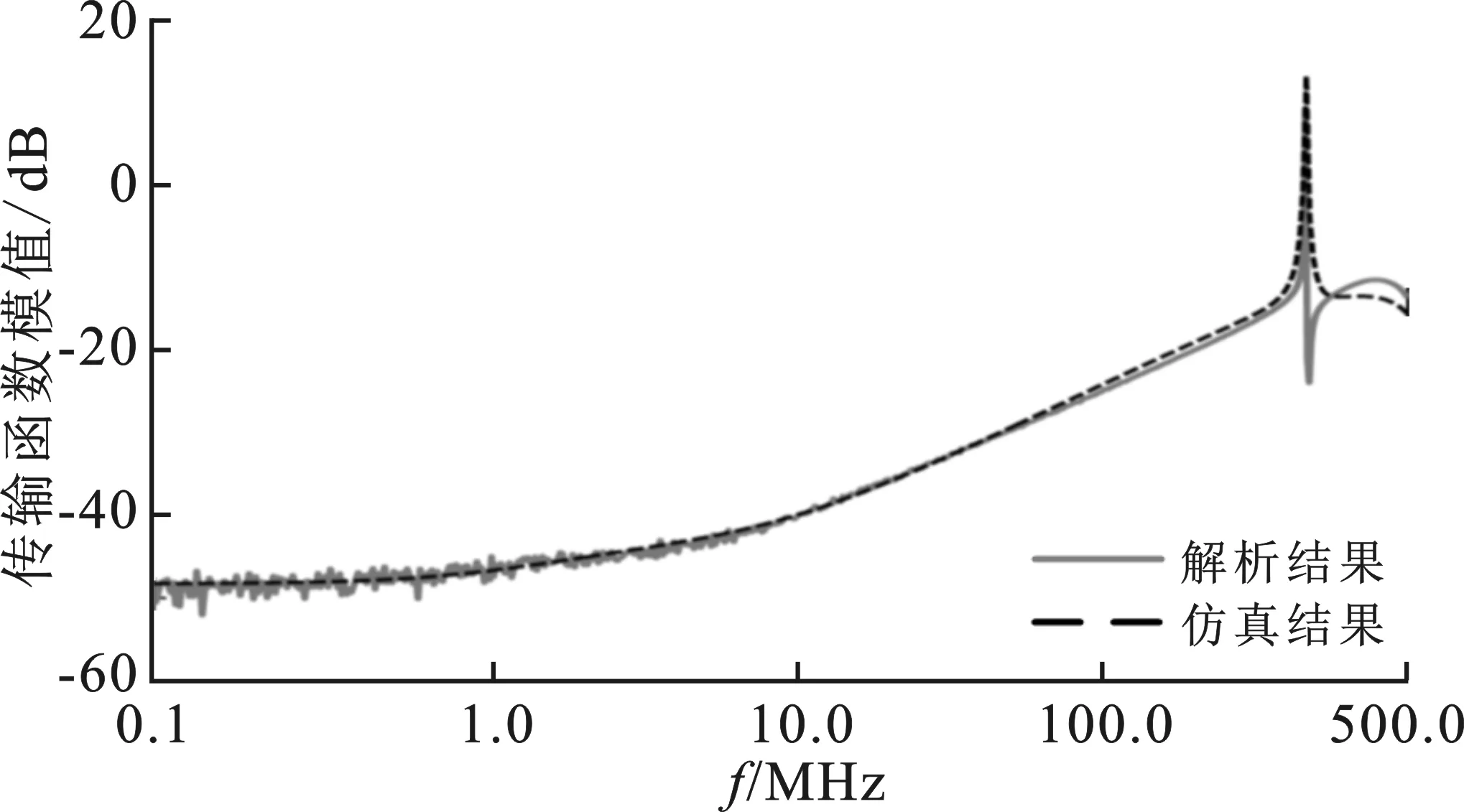
(a) 幅度比对

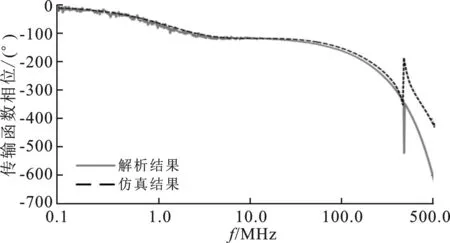
(b) 相位比对

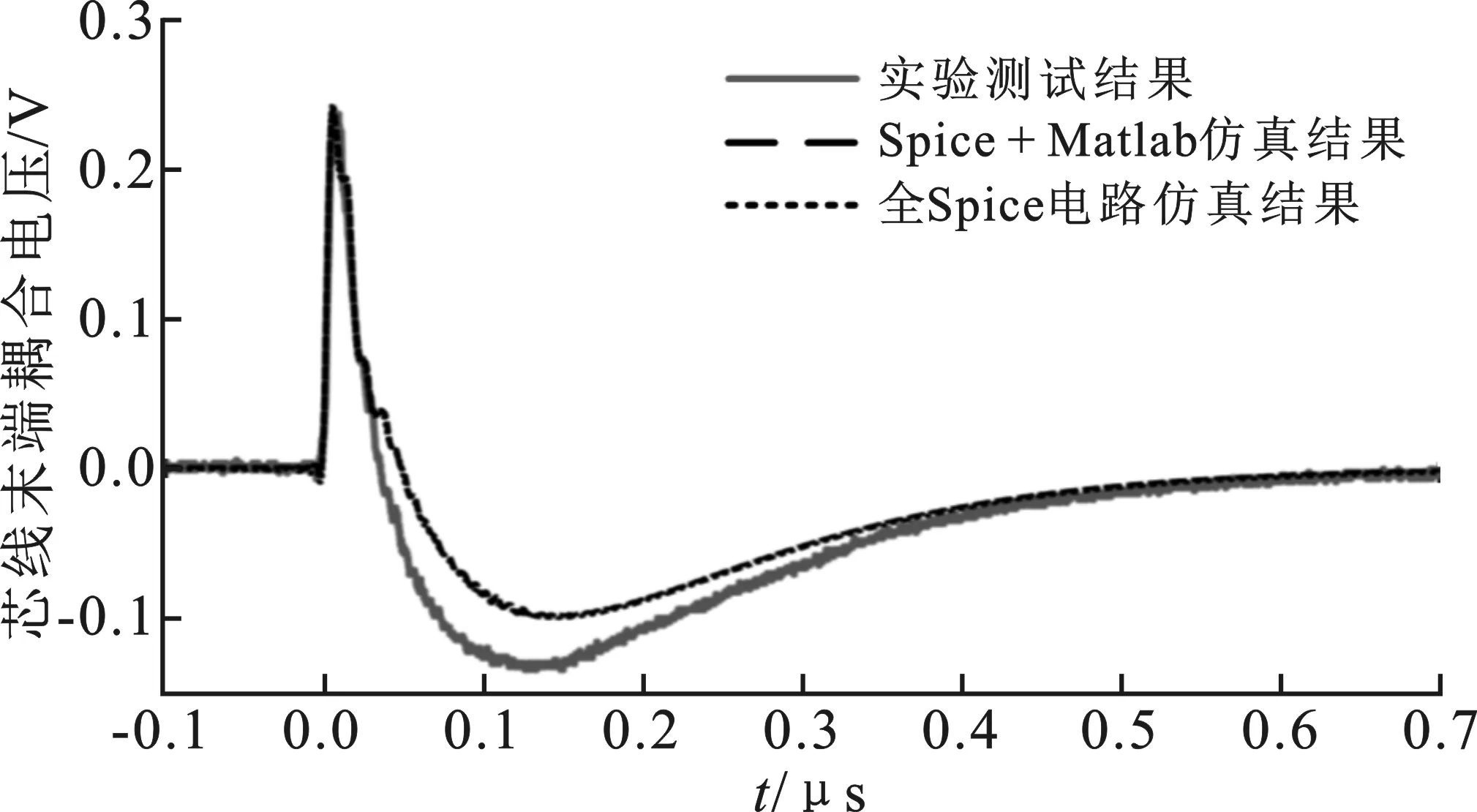
图11 芯线末端耦合电压的仿真与实验结果

最后，在完成以上各部分单独验证的基础上，对两项仿真方法进行整体性的验证。针对芯线末端耦合电压，实验测试结果、Spice+Matlab仿真结果、全Spice电路仿真结果比对如图11所示。可见，两种仿真方法得到的结果基本一致，且与实测结果在脉冲源峰值和整体波形上符合较好。仿真与实验的差异体现在低频相关的负向脉冲部分，这主要是由于在转移阻抗的测试过程中，受限于设备性能指标，缺乏低频部分(<0.1 MHz)的测量数据，因此造成低频区域上仿真精度相对偏低。

6 结束语

笔者针对同轴电缆感性脉冲电流注入的建模仿真问题，从分析其作用机理出发，通过将电缆屏蔽层视为传输单线，采用Spice建模的方法求取其耦合电流；按照三同轴法中的短路-短路法来获取电缆转移阻抗并应用到仿真中，同时也建立了其Spice电路拟合模型，从而提高了仿真的精度；对于屏蔽层与芯线间的耦合，给出了良好屏蔽假设和忽略转移导纳情况下两者间关系的解析方程，也建立了其耦合电路的集总近似模型，解决了脉冲电流注入全平台时域仿真的收敛性问题。最后在上述研究工作基础上，建立了同轴电缆感性脉冲电流注入的Spice+Matlab程序、全Spice电路建模两种仿真方法并进行了数值和实验验证。前者便于调整相关参数以分析其对结果的影响；后者则更利于处理受试设备端口为非线性负载的情况。

文中介绍的感性脉冲电流注入仿真方法，为电子设备抗强瞬态电磁干扰传导试验等提供了一种量化手段，可用于该类试验的设计、分析、效果预估等工作。后续将加深转移阻抗测试方法相关研究，特别是扩大测试频率范围，以进一步提高仿真精度。另外，对于多芯电缆的感性脉冲电流注入仿真问题，也将在文中基础上开展进一步的探究。