列车制动系统用杠杆螺栓S-N曲线试验研究

张亚军，赵春光，陈 沛，党恒耀，张欣耀

（1.中国船舶重工集团公司第七二五研究所，河南洛阳 471023；2.河南省船舶及海工装备结构材料技术与应用重点实验室，河南洛阳 471023；3.北京纵横机电科技有限公司，北京 100094；4.国家新材料生产应用示范平台（先进海工与高技术船舶材料），河南洛阳 471023）

随着列车运行速度的不断提高，制动系统的可靠性也越来越引起重视，并成为保障列车安全运行的一项重要指标［1-3］。作为高速列车盘形制动系统中的关键零件，制动杠杆螺栓在服役过程中常因受到反复的4 点弯曲应力和剪切应力作用而产生疲劳失效［4-5］。材料或零件的应力-寿命曲线（S-N 曲线）是名义应力抗疲劳设计法的设计依据。

材料的S-N曲线及其方程，通常将标准的光滑试样，按照不同的加载方式，依据GB/T 4337—2008《金属材料疲劳试验旋转弯曲方法》和GB/T 3075—2008《金属材料疲劳试验轴向力控制方法》等试验标准，通过成组法获得，有时还会辅以计算方法获得［6-8］。

零件的几何形状和边界条件千变万化，因此零件的S-N 曲线及其方程的获得并无标准可依。虽可在条件允许的情况下，结合零件服役时的受力模式，通过特殊的专用设备开展试验［9］获得，但更多的是利用材料的S-N 曲线转化为零件的S-N 曲线，这时通常需要考虑疲劳缺口系数、尺寸系数、表面质量系数、加载方式等多种因素［10］，尤其是当零件表面进行特殊处理时，还需要考虑表面处理工艺系数，而以上系数一般需要通过大量的试验获得，加之以上多种因素耦合效应的不确定性，使得通过材料的S-N 曲线准确转化为零件的S-N 曲线具有高试验成本和高风险性。对于列车制动杠杆螺栓而言，虽然有文献提及其疲劳验证试验台［11］，但是对加载方式、试验技术细节等并未进行交代，且该试验台无法用来进行以断裂为失效判据的S-N曲线试验。

本文以表面经过硬化处理的列车制动系统用杠杆螺栓为研究对象，分析其残余应力对疲劳裂纹萌生位置的影响，在分析其服役时受力特征的基础上，设计专用的试验夹具，建立基于应变片法标定受载点处轴向应力与弯曲应力的关系，采用变更施力点后的4 点弯曲加载方式，通过常用的电液伺服材料疲劳试验机完成该杠杆螺栓的S-N 曲线试验，并分析螺栓的断口特征，可为其预先疲劳寿命设计、工艺改进及工程应用提供依据。

1 杠杆螺栓

1.1 材质

杠杆螺栓的制造材料为42CrMo 钢，材料规格为36 mm，供货状态为热轧，热处理状态为淬火+回火。其化学成分和力学性能均满足标准GB/T 3077—2015《合金结构钢》要求，分别见表1和表2。

表1 杠杆螺栓材料的化学成分（质量分数）%

表2 杠杆螺栓材料力学性能指标

1.2 尺寸与加工处理工艺

杠杆螺栓全长314 mm，其中螺帽厚度为10 mm，螺杆长268 mm，螺杆直径为33 mm，其外形及尺寸示意图如图1所示。

图1 杠杆螺栓外形尺寸示意图（单位：mm）

杠杆螺栓主要加工与处理工艺为：下料→锻造→退火或高温回火→粗车→调质处理→精车→精车螺纹→螺栓通体表面淬火（硬化层深度1～2 mm）→低温回火→磁粉探伤→包装。

2 杠杆螺栓表面残余应力

疲劳裂纹通常萌生于材料或零件的表面，这是因为表面处于平面应力状态，易于变形而形成裂纹；同时，由于表面加工刀痕、运输碰伤、装配划伤等缺陷，都易因应力集中形成表面裂纹。但如果表面经过特殊处理后（如表面喷丸、表面超声、表面淬火等）产生残余压应力，将会阻止裂纹的萌生和扩展。因此，需要测量杠杆螺栓经过通体处理后是否会形成残余压应力，以及是否会对裂纹萌生造成影响。

采用XStress3000 G3型X射线应力仪，测量杠杆螺栓的表面残余应力。测量依据标准GB/T 7704—2017《X 射线应力测定方法》进行。辐射射线为CrKα 线，衍射晶面为α-Fe（211）晶面，应力常数K 为-318 MPa/（°），加速电压为30 kV，加速电流为6.7 mA，采用双固体位敏探测器，曝光时间为6 s。考虑杠杆螺栓的处理工艺和处理状态（通体淬火）以及所测量部位的代表性，选取9个测点，每个点沿与杠杆螺栓平行的x方向和与杠杆螺栓垂直的y 方向分别进行测量，测点位置如图2 所示，测量结果如图3 所示。图3 中，负值表示压应力。

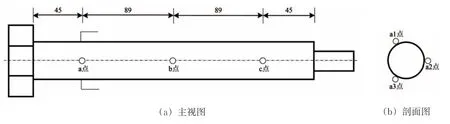
图2 杠杆螺栓残余应力测点位置（单位：mm）

从图3可见，杠杆螺栓表面不同位置处的残余应力全部为压应力，最小为-256 MPa（负号表示压应力），最大值为-579 MPa，平均值为-438 MPa。表面残余压应力，通常会抑制疲劳裂纹的萌生和扩展，提高材料的疲劳抗力，对延长杠杆螺栓的疲劳寿命是有利的。

图3 杠杆螺栓表面残余应力测量结果

3 杠杆螺栓受力特征

杠杆螺栓安装在盘形制动夹钳中左右2 侧杠杆的中间节点处，其主要作用是作为杠杆的中间支点，将单元制动缸产生的制动力传递到闸片上，确保车轮停止滚动，是制动夹钳单元的核心元件。根据其工作原理可知，杠杆螺栓主要承受单元制动缸产生的4 点弯曲横向力作用，可以简化为简支梁，其服役时受力与弯矩示意图如图4 所示。图中：A点和D 点为杠杆螺栓所受同向力的2 个作用点；B点和C 点为受到A 点和D 点反向力的2 个作用点；B’点和C’点为B 点和C 点2 个受力作用点变更后2个新的受力作用点；F，Q 和M 分别为作用在杠杆螺栓上的垂向力、剪力和弯矩。

图4 杠杆螺栓服役时受力与弯矩示意图

从图4 可见：在AB 之间和CD 之间杠杆螺栓会分别受到大小相等、方向相反的正、负剪力作用，剪力的大小等于支撑点或施力点所受的力（根据受力分析，A 点、B 点、C 点和D 点所受的力大小相等）；BC 之间的剪力为零。从A 点—B 点和D点—C 点弯矩线性增加，在B 点和C 点处弯矩达到最大值，BC 之间任何一点处均具有相等的最大弯矩。即杠杆螺栓受到4 点弯曲应力及1 对剪力作用，在线弹性范围内，其弯曲应力为

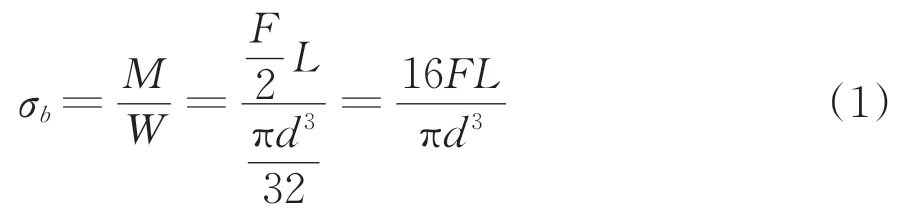
式中：σb为弯曲应力，MPa；W 为抗弯截面模量，mm3；L 为力臂的长度，即AB 段的长度，mm；d为螺栓直径，mm。

从式（1）可见，在保持弯曲应力不变的情况下，试验载荷F 和力臂L成反比。实际服役中，杠杆螺栓的支撑点A 与施力点B 靠得很近，2 个衬套之间几乎没有空隙，也就是说L很小，因此，要想有足够的刹车力，需要有较大的载荷F。要获得杠杆螺栓的S-N 曲线，就需要较大吨位的试验机，而试验机进行大吨位弯曲加载时试验频率不会很高（一方面，大载荷下螺栓产生的变形相对较大，受试验机原理的控制，大变形下试验机作动器只能产生较低的频率；另一方面，过高的试验频率，往往会使试样件产生热效应，从而降低试验结果的准确性和可靠性），要获得杠杆螺栓的S-N 曲线，还需要花费较长的试验时间和较高的试验成本。为此，考虑杠杆螺栓材料的均匀性及通体处理工艺，在保持弯曲应力不变的前提下，可以通过增加力臂L而达到降低载荷F的目的，但应考虑试验机载荷容量的限制，即最大的试验载荷不能超过试验机的载荷容量。为此，在确保弯曲应力不变的情况下增加力臂L，分别将施力点B 点和C 点向杠杆螺栓中心平移至B’点和C’点，使得力臂由AB段和DC段的实际距离28.25 mm 增加为AB’段和DC’段的距离81.25 mm，力臂L增加约3倍，从而在弯曲应力不变的情况下，使得试验载荷约降至原始最大试验载荷的1/3 倍，理论上这样处理不会影响杠杆螺栓的疲劳寿命，仅会改变其断裂位置，即从原来弯矩下突变点B点和C点附近，转变至相同弯矩下新的突变点，即B’点和C’点附近，相应的剪力和弯矩变化见图4（b）和图4（c）中的虚线部分。

4 杠杆螺栓受载点拉伸应力与弯曲应力关系

杠杆螺栓的弯曲应力可以根据式（1）计算得到。而对于受载点附近的拉伸应力，金宗哲［12］等基于拉伸和弯曲破坏在力学上同样遵循最大拉应力破坏准则，给出了拉伸应力与弯曲应力的关系为

式中：σt为拉伸应力，MPa；σb为弯曲应力，MPa；△为材料破坏损伤区高度，mm；根据不同的材料，△=0～0.5h，h 为试件的厚度，此处为杠杆螺栓的直径，mm。

根据式（2）可知，弯曲应力理论上是拉伸应力的1～2 倍。由于损伤的微观性，目前并没有合适的方法能够准确测量出不同△的大小。为此，采用在杠杆螺栓施力点正对面粘贴应变片的方法，标定出载荷F 和应变ε 的关系。根据式（1），就可以最终建立弯曲应力σb与拉伸应力σt的关系。

5 杠杆螺栓S-N 曲线试验方法和结果

5.1 试验方法

首先，设计4点弯曲的试验夹具。

其次，在MTS 319—250 kN 电液伺服疲劳试验机上参考标准GB/T 3075—2000《金属材料疲劳试验轴向力控制方法》进行试验。模拟螺栓的受力情况，采用上下各2 个支撑辊的4 点弯曲加载疲劳试验，杠杆螺栓与支撑点处套上服役时用的耐磨尼龙衬套。试验采用载荷控制模式，载荷比为0.1，试验频率为3.0 Hz。采用4 组不同的应力水平（对应的4 个载荷水平范围分别为9.5～95，11～110，12.5～125 和14～140 kN），每个应力水平下完成3～5 件杠杆螺栓的疲劳试验。当杠杆螺栓断裂或循环寿命N 达到3.5×106次时终止试验，记录其断裂位置。疲劳试验数据处理参照标准GB/T 24176—2009《金属材料疲劳试验数据统计方案与分析方法》及相关资料进行。试验过程图如图5所示。

图5 杠杆螺栓试验过程

然后，在螺栓上施力点的正下方沿轴向方向贴上应变片，采集应变片测量应变数据，据此计算螺栓沿轴向方向的应力。杠杆螺栓轴向应力的标定过程如图6所示，应变片的粘贴位置如图7所示。

图6 标定杠杆螺栓轴向应力

图7 应变片在杠杆螺栓的粘贴位置示意图（单位：mm）

最后，选择部分杠杆螺栓断口，在扫描电镜下观察疲劳裂纹的萌生和扩展情况。

5.2 试验结果

5.2.1 不同存活率下S-N曲线

按照以上试验方法，获得了4 组载荷作用下的疲劳寿命数据，如图8所示。

从图8 可见：在4 级应力水平下，应力越小，疲劳寿命越高；每级应力水平下的试验数据，有一定的分散性。

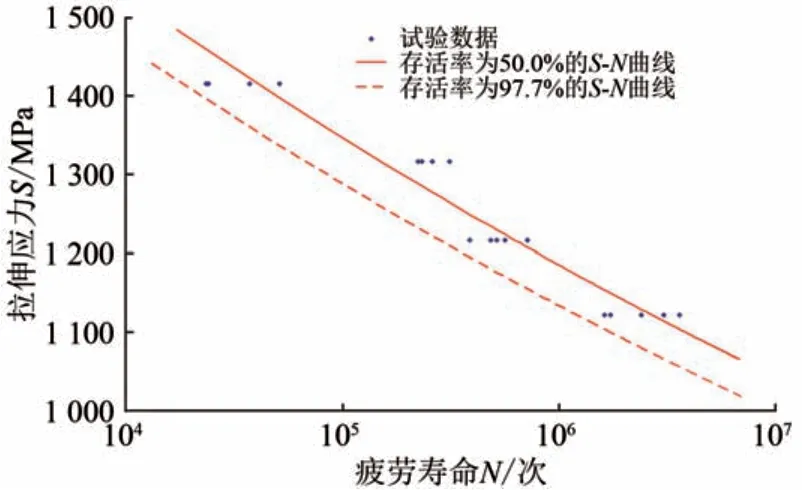
图8 不同存活率下杠杆螺栓S-N试验数据及拟合曲线

对试验数据进行拟合处理，可以获得2 种不同存活率P 下相关系数R 为0.982 0 时杠杆螺栓的SN曲线方程为

从图8 和式（3）可见，杠杆螺栓的S-N 数据可以较好地用幂函数表达，与常见金属材料的S-N数据分布具有相似性。

需要说明的是，S-N 曲线中的应力“S”为最大拉伸应力。由于表面残余压应力可以抵消一部分外力，其存在使得实际作用在杠杆螺栓上的外力（轴向最大拉伸应力减去沿螺栓方向上的残余应力）小很多，这样就等同于显著提高了螺栓表面的疲劳抗力，从而利于延长其疲劳使用寿命。

5.2.2 疲劳断口形貌

宏观观察发现，所有杠杆螺栓均断在如图4（a）中所示的B'点或C'点附近，如图9所示。

图9 杠杆螺栓宏观断裂位置

从图9 可见：所有杠杆螺栓理论预测断裂位置与实际试验后断裂的位置相吻合，表明变更施力点位置加载方法具有合理性，即对于通体处理后杠杆螺栓而言，可以通过调整杠杆螺栓施力点位置而增加力臂、降低载荷，从而在常规小吨位疲劳试验机上完成杠杆螺栓的S-N曲线试验。

采用Quanta650 扫描电镜，观察杠杆螺栓的疲劳断口发现：所有试样断口平齐，硬化层轮廓清晰可见，整个螺栓断面的疲劳断口约分为2 个颜色不同的区域，且2 个区域的裂纹扩展速率不同；疲劳裂纹萌生于螺栓表面淬硬层和内部材料交汇处，该处似有冶金缺陷，如图10（a）所示。

为确定裂纹萌生位置处是否有冶金缺陷存在，对裂纹萌生部位进行逐级放大的倍数观察，分别如图10（b）、10（c）和10（d）所示。裂纹萌生位置放大50 倍显示，裂纹萌生后呈放射状向四周扩展；放大1 000 倍显示，裂纹萌生处附近呈菊花状，“花瓣”为裂纹在不同面扩展交汇后形成的脊；放大2 000 倍显示，裂纹萌生位置附近呈现明显的梯度，如同1 个“深坑”，且可看到大量近似平行的层状裂纹分布在“深坑”的不同深度；而并没有发现有明显的夹渣、孔洞等冶金缺陷存在。

图10 疲劳裂纹萌生位置观察

6 分析与讨论

考虑到大多数情况下，裂纹一般萌生于材料或零件的表面，这是由于表面不受约束，容易变形，且由于加工、装配、热处理等工序都有可能对材料或零件的表面造成损伤，为裂纹萌生提供便利，除非材料或零件内部有冶金缺陷，如明显的夹杂、气孔、偏析等缺陷存在。然而，如果材料或零件没有明显的冶金缺陷，而表面又经过特殊的处理，如杠杆螺栓经过了调质+通体淬火+低温回火的处理，改变了表面的自由状态，使其表面分布1层残余压应力，而压应力通常会提高材料的疲劳抗力，阻碍裂纹的萌生和扩展，这样就有可能改变裂纹从表面萌生的可能性，从而提高杠杆螺栓的疲劳寿命。

从前面的测试结果可知，螺栓表面残余压应力平均值约为-440 MPa。材料或零件正常情况下所受的力是平衡的，只要有残余压应力存在，就必然会有大小相等的残余拉应力存在，二者大小相等，方向相反。因为在残余压力作用下，疲劳裂纹通常不易于萌生和扩展。为此，工程中的许多零件，常常通过不同的处理方法，如表面喷丸、表面超声、表面淬火、表面渗碳或渗氮等，使零件表面产生1层残余压应力，以抑制疲劳裂纹的萌生和扩展，提高零件的使用寿命。有研究者［13-14］就曾采用表面超声处理的方法，分别在7B50-T7751 铝合金和Ti-6Al-4V 钛合金表面引入残余压应力，以提高2种材料的疲劳性能。也有研究者［15］为了降低焊缝处的残余拉应力，采用后焊冷却处理工艺方法，在304L 不锈钢焊缝处引入残余压应力，以提高其疲劳抗力，并取得较好的效果。对于杠杆螺栓而言，在表面硬化层与内部材料的交界处附近，必然存在1 个零应力区，即应力梯度变化最显著的地方，这个地方恰恰是零件最薄弱的地方，也是疲劳裂纹最容易萌生的地方，因此，杠杆螺栓疲劳裂纹在表面硬化层与内部材料的交界处附近萌生。

7 结 论

（1）经过硬化处理后的杠杆螺栓表面分布1 层残余压应力，最小值为-256 MPa，最大值为-579 MPa，平均值为-438 MPa。压应力会阻碍疲劳裂纹的萌生与扩展，使得疲劳裂纹并未萌生于螺栓表面，而是萌生于表面硬化层和内部材料的结合处；该位置附近并未发现有明显的冶金缺陷，疲劳裂纹萌生于此处可能是由于该处的应力梯度变化最为显著所致。

（2）所有杠杆螺栓宏观断口平齐，且断裂均发生在变更施力点后预测的位置附近，表明理论预测的杠杆螺栓断裂位置与实际试验结果一致，证明变更施力点加载方法的合理性，即对于通体处理后杠杆螺栓而言，在保证弯曲应力不变、仅改变施力点位置的情况下，试验时将施力点向杠杆螺栓中心平移以增加力臂，降低试验载荷，从而实现在常规小吨位疲劳试验机上完成杠杆螺栓S-N曲线试验。

（3）不同存活率下、相关系数为0.982 0 的杠杆螺栓的S-N 曲线方程均可用幂函数模型进行较好的表达，说明杠杆螺栓与常见金属材料的S-N数据分布规律具有相似性，可用于杠杆螺栓的安全设计和疲劳寿命评估。