地铁站台光照动态调控方法

2021-08-12段中兴李继斌

中国铁道科学 2021年4期

段中兴，李继斌

（1.西安建筑科技大学信息与控制工程学院，陕西西安 710055；2.西安建筑科技大学西部绿色建筑国家重点实验室，陕西西安 710055）

城市轨道交通以其巨大的社会和经济影响成为城市战略发展的重点，而地铁运营线路是最主要的城市轨道交通制式［1］。地铁站作为一种空间封闭的特殊建筑形态，其光环境依靠人工照明营造，具有照明时间长、强度高和能耗大的特点。中国交通运输部2016年数据显示，地铁实际照明负荷占地铁系统设备总负荷的20%～30%，单位面积照明能耗超出国家标准的14.2%～16.1%［2］；欧洲SEAM4US项目组给出了巴塞罗那某试点地铁站的分项能耗数据，其中照明年能耗为229 067.17 kW·h，在分项能耗中所占比例最大（37.46%）［3］。地铁建设的快速发展以及地铁站单位面积照明的高能耗，使得地铁站照明节能变得更加必要和紧迫。

近年来随着半导体照明技术的发展，LED 被广泛应用于各种照明场所，尤其是大功率LED 光源光照参数（如光强、色温等）的多样性和可控性为营造舒适光环境、挖掘照明节能的潜力创造了有利条件，由此一些利用LED 光源光照参数可调特点的照明控制方法被相继提出，为丰富照明控制理论和技术手段提供了新的思路和方向。Qin等［4］利用数据挖掘技术提出了一种基于交通流量分布、交通组成和车速分布的隧道LED 照明动态调节方法；Casals 等［5］利用K-means 聚类方法对时间维度的地铁站客流量数据集进行聚类，建立调光时间表指导地铁站LED 的调光控制；Lai 等［2］针对地铁站厅提出了一种基于节能方案的照明系统智能模型，系统在不同时间段自动调整每个功能区域LED 的亮度。这些研究成果对地铁站的光照调控研究具有很好的借鉴作用，但现有研究中地铁站光照调控方式为线性调光，易造成过度照明，不利于节能，且由于未考虑邻近区域光照的耦合关系，难以实现精确调光。

本文以全人工照明的地铁地下标准岛式站台为研究对象，将站台公共区划分为多个子区域，考虑子区域照度的耦合关系，建立站台照明模型进行照明模拟，获取照度数据及其等式约束，建立最小能耗光照调控模型；针对遗传算法收敛速度较慢和局部寻优能力较弱的不足，基于反向学习策略提出自适应反向学习方法，用于改进遗传算法；依据子区域人群密度确定其照度设定值，作为光照调控模型的输入，利用改进算法对光照调控模型进行求解，得到站台LED灯具的最佳调光比。

1 光照调控模型

1.1 站台照明模型

照明系统中，通常采用照度作为光照强度的定量指标，物体的照度应与人眼视力和设计要求相吻合，强调了在合理的范围内控制照度的必要性，避免因过度照明而造成浪费［6-7］。因此，选取照度作为光照调控的基本参数。

站台光照调控区域为站台公共区，将公共区划分为多个子区域，考虑邻近子区域光照的耦合关系，需获取多组光源分别为各子区域提供的最大照度作为调控系数，将其定义为“耦合照度系数（Coupled illumination coefficients，CIC）”。例如，区域A 和区域B 的照明均由光源1、光源2、光源3提供，3个光源为区域A提供的最大照度EA1，EA2，EA3定义为区域A的CIC，为区域B提供的最大照度EB1，EB2，EB3定义为区域B的CIC，光源光通量的变化将同时引起2 个区域的照度变化，即区域的照度相互耦合。相较于不考虑照度耦合关系的线性调光方式，利用CIC进行光照调控可实现精确调光。

获取子区域CIC及其等式约束的流程如下。

（1）基于站台基本功能分区进行公共区的子区域划分，利用站台形制和建筑材料调研数据在DI⁃ALux软件中建立站台三维仿真模型；

（2）依据子区域划分和照明设计标准，结合站台灯具调研数据，在站台三维仿真模型中对LED 灯具进行选型、布置和分组，建立站台照明模型；

（3）利用站台照明模型进行照明模拟，获取子区域的CIC及其等式约束。

1.1.1 站台三维仿真模型

以西安地铁4 号线某站台为研究对象，站台平面图如图1 所示。该站台为典型的标准地下岛式站台，包括轨行区和公共区2 个基本功能区域，其中公共区分为站台边缘和候车区2 个部分。站台光照来源于公共区下照式灯具提供的基础照明和轨行区挂墙式广告灯箱提供的广告照明。

图1 某地铁站台平面图

公共区的子区域划分如图2 所示，共分为9 个子区域（区域A—区域I），建立的站台三维仿真模型如图3所示。

图2 公共区子区域划分

图3 某地铁站台三维仿真模型

1.1.2 站台照明模型

对站台灯具进行选型、布置和分组。文献［7］中规定的站台（地下）照度标准值为150 lx，国内地下站台平均照度值上限一般超过国家标准的40%以上（达到210 lx），因此，将站台照度的调节范围确定为150～210 lx，考虑5%～10%的设计余量，即站台照明最大平均照度为220～230 lx。

站台灯具选型和布置如下。

（1）该站台2 侧轨行区共均匀分布36 个12 封（3 m×1.5 m）广告灯箱（灯箱功率400 W，表面光通量18 000 lm，内部为LED 灯条）。因此，在DIALux 软件灯具库中选择功率100 W、光通量4 500 lm、显色指数85、长度3 m 的挂墙式LED 灯条，每4 个灯条模拟1 个广告灯箱，共布置144 个灯条，灯具布局如图4（a）所示，灯条以橙色边框蓝色填充表示。

图4 某地铁站台灯具布局

（2）该站台公共区灯具为T5 荧光灯管（功率18 W，布灯416 盏）。该灯管光通量不可调，故不能用于光照动态调控。因此，在DIALux 软件灯具库中选用光通量可调的LED 灯具对公共区照明系统进行改造，该LED 灯具为功率47 W、光通量2 248 lm、显色指数85的方形嵌入式灯具，共布置133 个灯具，灯具布局如图4（b）所示，灯具以橙色边框蓝色填充表示。

照明模拟结果显示站台最大平均照度为227 lx，灯具选型与布局满足设计要求。

实际站台中广告照明的照度不变，为子区域提供恒定照度。因此，光照调控过程仅需对基础照明灯具进行分组。以区域A、区域B 和区域C 为例，依据子区域划分和灯具布置，将区域A 内灯具、区域B 内灯具、区域C 内灯具、区域A 与区域B 边界灯具、区域B 与区域C 边界灯具分别划分为1 个灯组，如图5 所示，每个虚线框内灯具为1 个灯组。其余子区域灯具分组规则类同，将公共区LED 灯具共分为15 组，见表1。至此，站台照明模型建立完成。

图5 公共区灯具分组（区域A、区域B和区域C为例）

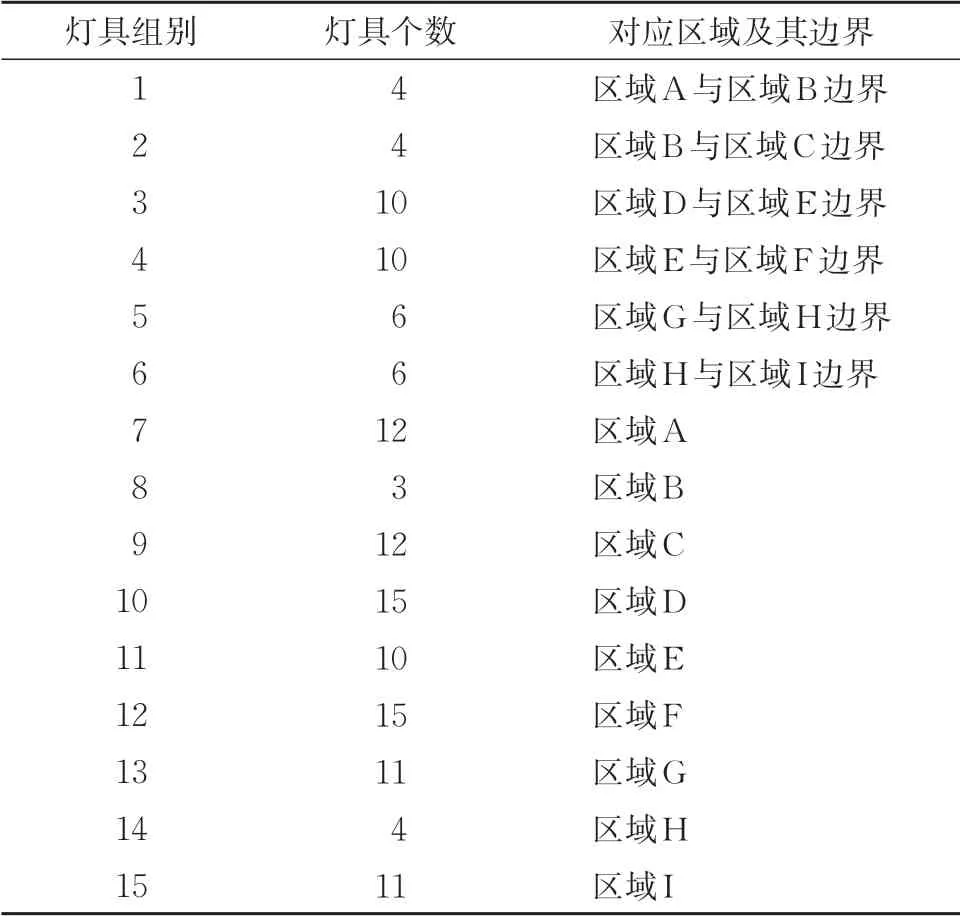
表1 公共区LED灯组

1.1.3 公共区子区域CIC及其等式约束

利用站台照明模型进行照明模拟，获取公共区子区域CIC并建立其等式约束的步骤如下。

（1）全区照明模拟，如图6（a）所示，得到全区灯具为子区域提供的最大照度。

（2）轨行区广告照明模拟，如图6（b）所示，得到广告灯箱为子区域提供的恒定照度。

（3）公共区LED 灯组照明模拟，如图6（c）所示（以灯组11为例），得到子区域的CIC。

图6 某地铁站台照明模拟渲染图

（4）子区域CIC 等式约束建立。以区域A 为例，将步骤（1）中得到的全区照明为区域A 提供的最大照度记为EA-max，步骤（2）中得到的广告照明为区域A 提供的照度记为EA_adv，则基础照明为区域A 提供的最大照度为EmaxA_basic=EA-max-EA_adv。步骤（3）中得到的区域A 的CIC 记为(EA1，EA2，…，EA15)，且满足等式约束为EmaxA_basic=EA1+EA2+…+EA15，其余子区域类同，故子区域的CIC满足等式约束为

其中，

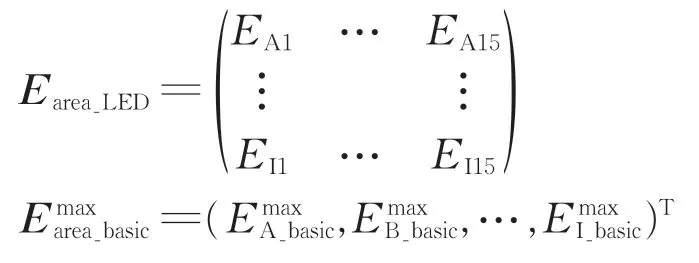
式中：Earea_LED表示由各子区域CIC 构成的（9×15）维CIC矩阵；L表示元素均为1的（15×1）维列向量。

1.2 光照调控模型

1.2.1 最小能耗优化光照调控模型

站台光照动态调控方法的基本思想为：各子区域的人群密度不同照度需求也不同，则照明系统根据各子区域照度需求自动更改LED 灯组照度。各子区域的照度是相互耦合的，且灯组数量大于子区域数量，因此LED 灯组可以有多种不同的照度组合达到各子区域需求的照度水平，在众多的灯组照度组合中，搜寻到使照明能耗最小的照度组合，实现光照的最优控制。

区域A—区域I 的基础照明照度需求为Earea_basic=(EA_basic，EB_basic，…，EI_basic)T，当灯组1～灯组15 的调光比向量α=(α1，α2，…，α15)T时，可满足各子区域照度需求，基于式（1），有等式约束为

光照动态调控的目的是满足子区域照度需求的前提下，探究照明系统的最小能耗运行模式，即满足照度需求的前提下寻找电能W 的相对最小值。站台公共区使用的LED 灯具型号相同，忽略其电阻值的微小差异性，假设其额定电流为I，电阻为R，则照明系统t时间内消耗的总电能W为

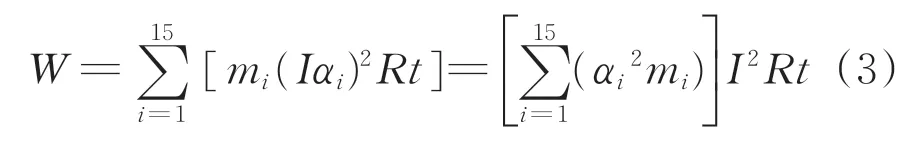
式中：mi为第i组灯的灯具个数，i＝1，2，…，15。

s.t.

Earea_LEDα=Earea_basic

1.2.2 等式约束降维处理方法

对于优化问题中等式约束的处理，通常采用的方法是等式约束松弛法和双不等式约束法，但是等式约束松弛法会改变优化拓扑空间，双不等式约束难以获得可行解［8］。基于变量独立性分析的等式约束降维处理方法，将等式约束转化为多目标，再求解无等式约束多目标优化问题，可以使等式约束严格满足的同时降低系统维数，避免了等式约束松弛法和双不等式约束法的弊端。因此，采用变量独立性分析对光照调控模型中的等式约束进行处理。

设公共区每个灯组的调光比为1 个优化变量，共15个优化变量；每个子区域的CIC满足1个等式约束，共9 个等式约束。由于存在等式约束，相互独立的变量最多只有15-9＝6 个。因此，下文选取6 个优化变量作为自由变量，其余9 个非自由变量由9个线性等式约束求解得出。

采用Gauss-Jordan 消元法将CIC 矩阵Earea_LED变换为简化行阶梯形矩阵来选取自由变量，阶梯矩阵每1 个阶梯对应调光比向量α=(α1，α2，…，α15)T中的1 个非自由变量，其余变量为自由变量。根据求得的行阶梯形矩阵，选取子区域边界灯组（灯组1—灯组6）的调光比α1,α2,…,α6作为自由变量，子区域内灯组（灯组7—灯组15）的调光比α7,α8,…,α15通过自由变量确定，由此可将式（2）表示为

解式（5）中的线性方程，将α7，α8，…，α15表示为自由变量向量αfv=(α1，α2，…，α6)的函数为

由式（6）将式（4）所示的含等式约束单目标优化模型转换为1 个无等式约束多目标优化模型，构造新的目标函数F(αfv)为

s.t.

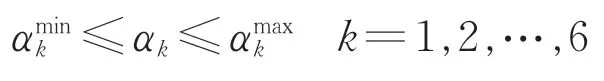
其中，

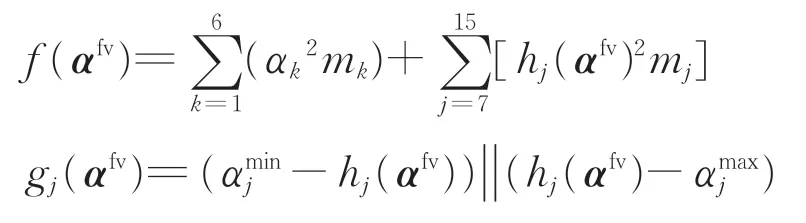
式中：f (αfv)为降维处理后的等效表达；gj(αfv)为降维处理后非自由变量取值范围的不等式约束。

2 基于自适应反向遗传算法的光照最优控制

遗传算法（Genetic algorthm，GA）是一种启发式优化算法，具有较强的鲁棒性，适用于多目标、非线性优化问题的求解。江等［9］将遗传算法应用于求解铁路集装箱班列始发时刻的优化模型，使集装箱在办理站停留时间最短；麻等［10］利用双编码层的节能操纵遗传算法求解节能操纵优化模型，优化效果优于常规操纵仿真算法；李等［11］建立了综合快运方案优化模型并利用遗传算法进行求解，降低了运输总成本。鉴于遗传算法在求解优化模型方面的适用性，将其用于光照调控模型的求解。

遗传算法存在收敛速度较慢和局部寻优能力较差的不足，为此，引入反向学习（Oppositionbased learning，OBL）［12-13］对遗传算法进行改进，以提高算法性能。OBL 理论中，实数γ ∈[a，b]的反向数定义为=a+b-γ。文献［11］的试验结果表明，将反向学习直接引入传统遗传算法构成反向遗传算法（OBL-GA），引入1 个随机解（染色体）及其对应的反向解（抗染色体），对算法性能提升有限。原因在于当种群的染色体离全局最优解相对较远时，抗染色体会在前期迭代中急剧占据种群，因此随后的迭代中抗染色体可能无效甚至对收敛到最优解产生负面影响。

Rahnamayans 等［14］基于反向数提出了准反向数为q=rand[(a+b)/2，]，Ergezer 等［15］基于准反向数提出了准反射反向数为qr=rand[γ，(a+b)/2]，准反向数和准反射反向数相较于反向数寻优效率更优。因此，借鉴准反向数和准反射反向数寻优的思想，提出一种基于最优目标值的自适应反向学习（Adaptive opposition-based learning，AO⁃BL）方法，对遗传算法进行改进，构成自适应反向遗传算法（AOBL-GA）。

AOBL-GA 求解光照最优控制问题的过程如下。

（1）初始化调光比种群A(t)，A(t)由n个不同的调光比向量αfv=(α1，α2，…，α6)组成。

（2）若当前迭代次数t 小于迭代次数限值，则进行步骤（3），否则跳转至步骤（7）。

（3）计算A(t)中n个αfv对应的目标值F(αfv)和平均目标值Fav(αfv)，若其中有p（p＜n）个较劣调光比向量对应的F(αbad)≥Fav(αfv)，则计算p 个αbad分别对应的AOBL 调光比向量其向量元素计算方法为

其中，

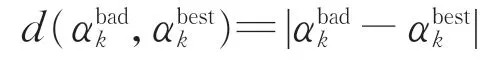
（5）对N（t）进行交叉，变异操作产生新调光比种群A（t＋1）。

（6）迭代次数＋1（即t+1 替换为t），返回步骤（2）。

（7）迭代结束。

（8）输出A（t）中最小目标值Fmin(αfv)对应的最优调光比向量αbest。

由于AOBL-GA 是自适应的，反向搜索区间随迭代次数的增加而变小，使得迭代后期原染色体和抗染色体均在全局最优解的邻域内，避免了迭代后期抗染色体对收敛到全局最优解产生的负面影响。AOBL-GA 利用每次迭代中最优目标值个体的先验信息自动确定反向搜索区间，在每次迭代过程中引入较劣个体的自适应反向个体，保证迭代过程中优良基因不被丢失的同时保持算法的开发能力，提高遗传算法的收敛速度和局部寻优能力。

3 试验验证

为验证AOBL-GA 的性能，进行算法对比试验；为验证动态调控方法的调控效果，进行光照调控模拟试验。由于光照调控模拟试验中需要利用算法对比后的最优算法求解调光比，因此，需首先进行算法对比试验，其次进行光照调控模拟试验。

3.1 算法对比试验

将AOBL-GA 与粒子群算法（PSO）、竞赛选择遗传算法（Tournament selection-Genetic algo⁃rithm，TS-GA）和反向遗传算法（OBL-GA）进行对比试验。设置算法最大迭代次数为200，粒子群算法的群体规模为40，惯性权重由0.9逐渐递减至0.4，学习因子均为2；遗传算法的种群规模为40，交叉概率为0.6，变异概率为0.03。

设计4 组试验，分别对应4 种子区域照度设定值，见表2。

表2 不同照明场景的子区域照度设定

利用每种算法分别对每组实验进行30 次重复试验，即每种算法共进行120 次试验，统计每种算法在30 次重复实验中的最大、最小、平均适应度以及适应度标准差，试验结果见表3。

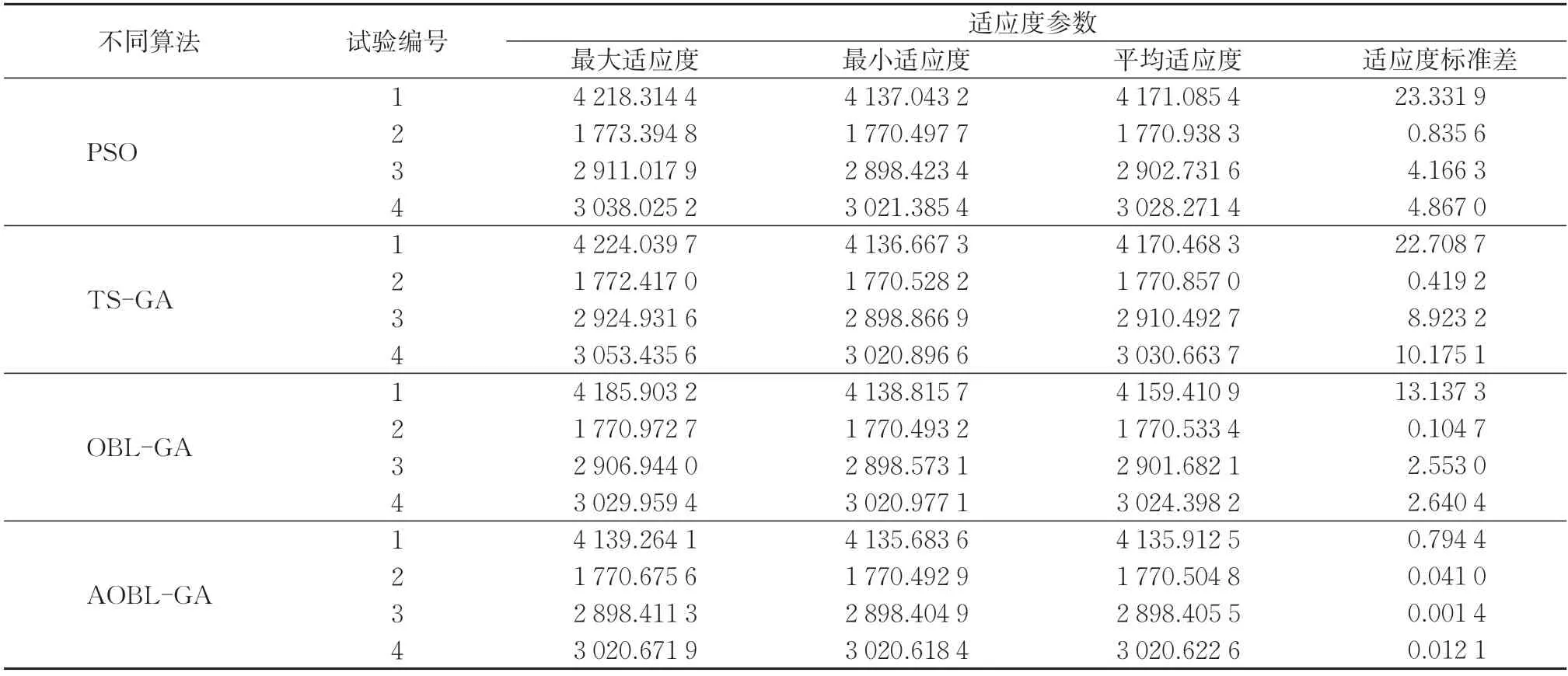
表3 不同算法照明模拟试验结果

由表3 可知，AOBL-GA 与其他3 种算法相比，4 组试验对应的适应度最大值、最小值、平均值和适应度标准差均更优，表明AOBL-GA 局部寻优能力更强且稳定性更好。

选择各算法在第10 次试验的适应度变化曲线作为展示，观察算法收敛速度和寻优能力，适应度变化曲线如图7所示。

图7 不同照度设定适应度变化曲线

由图7 可知，AOBL-GA 和其余3 种算法相比，4 组试验对应的适应度曲线收敛速度均更快，在迭代40 余次之后即能迅速收敛到最优值附近，表明AOBL-GA具有更快的收敛速度。

算法对比试验结果表明，AOBL-GA 相比于其他3 种算法在收敛速度、局部寻优能力和稳定性方面均更优。

3.2 光照调控模拟试验

动态调控方法的调控效果主要包括照度调控效果和照明节能效果。因此，进行光照调控模拟试验，从2 个方面验证动态调控方法的调控效果：①光照调控模型的可行性验证；②动态调控方法的节能性验证。

3.2.1 光照调控模型可行性验证

利用AOBL-GA 对光照调控模型进行求解，得到4 种照明场景对应的LED 灯组最优调光比见表4；将调光比输入站台照明模型进行照明模拟，得到照度模拟值，将其与照度设定值作比较，讨论光照调控模型的可行性，照度模拟值和设定值的比较见表5。

表4 不同照明场景最优调光比

由表5 可知，求得的照度模拟值和设定值之差绝对值不超过2 lx，照度偏差保持在1.33%（2 lx/150 lx≈0.013 3）以内，调控结果准确。试验结果表明，光照调控模型可实现精确调光，能够满足子区域照度需求，模型具有较强的可行性。

表5 不同照明场景照度设定值与模拟值比较

3.2.2 动态调控方法节能性验证

由于广告照明照度恒定，仅需比较基础照明节能效果。西安地铁4 号线工作日时刻表分为高、中、低峰期，该站台末班车到站时间为23：36，闭站时间为23：45，高峰期（7：00—9：00，17：00—19：00）内开启所有基础照明灯具（100%），中峰期（9：00—17：00，19：00—21：00）内开启80%的基础照明灯具，低峰期（6：00—7：00，21：00—23：45）内开启50%的基础照明灯具。由T5 荧光灯管参数计算得到该站台基础照明日电耗为416个×0.018 kW×(1.0×4 h＋0.8×10 h＋0.5×3 h)＝101.088 0 kW·h。

考虑站台实际人数（人数统计数据显示，站台人数在9～625 人区间内变化），定义站台照度调节范围见表6。表6中，站台人数按中国行进行人服务水平分级标准建议表中的行人空间占有量划分［16］，照度变化区间长度（15 lx）为极端工况下满足站台照度均匀度规定的临界值。