重载铁路直接供电方式下牵引回流分配及影响因素
2021-08-12曹晓斌王满想朱传林何玉峰
曹晓斌,王满想,朱传林,何玉峰
(1.西南交通大学电气工程学院,四川成都 610031;2.国家电网山东省电力公司泰安供电公司,山东泰安 271000)
随着我国铁路高速发展,为适应铁路运输需求,铁路站场不断扩建,站场牵引回流情况越来越复杂[1-2]。目前,站场中钢轨与回流线电流的分配比例是不明确的,这使得站场普遍存在部分线路中电流很大或很小的现象。钢轨和回流线中流过的电流很小时,说明该部分线路失去了牵引回流的作用;电流很大时,通常会引起钢轨电位过高、绝缘节拉弧、等阻线烧断、电务设备损坏等问题[3-4]。回流系统中各线路的回流分配比例不仅可以作为检测站场电务设备安全性能的指标,也是前期回流系统设计的重要依据,如钢轨电流的变化是扼流变压器容量配置的参考[5]。因此,研究牵引回流的分配情况至关重要。
重载铁路站场直接供电方式下牵引回流分配的影响因素有线路参数、吸上线的位置和数量、地回流、线路间耦合作用、上下行钢轨间距等。文献[6-9]通过计算钢轨和综合地线的等效阻抗,得到牵引回流在钢轨与综合地线之间的分配比例,指出采用地网不载流的接线方式可以减小地回流。文献[10-11]搭建了牵引供电系统回流线分流模型,分析回流线的作用和效果,但该研究未考虑接触线和供电线与回流线的耦合作用。文献[12-14]将钢轨与回流线看作1 条等值导线,通过计算“回流线+钢轨”等值自阻抗与接触线间互阻抗后,指出单线区段的钢轨电流约为接触线电流的一半强,复线区段的钢轨电流与上下行接触线的电流代数和成正比,但该研究未对钢轨和回流线的单独影响进行分析。
本文以某重载铁路站场牵引回流的测量结果为依据,采用控制变量法,单独考察各个因素的耦合影响,最终找出了回流电流分配系数的产生机理,并研究给出了各导线之间的回流分配比例的取值范围,为进一步量化回流系统分配规律的研究提供了理论依据。
1 现场试验
某重载铁路站场供电方式为带回流线的直接供电方式,牵引变电所位于站场上行线路的外侧中部。测量对象为站场外预告信号机至进站信号机的复线区段,长为1 000 m,距离进站信号机443 m处存在电分相,即当有列车行驶至预告信号机时,牵引电流从牵引变电所经接触线给列车供电,列车将牵引电流泄入钢轨后,牵引电流通过钢轨和回流线流回牵引变电所。预告信号机与进站信号机处上下行侧扼流变压器的中性点通过横向连接线连通。站场未铺设贯通地线,钢轨与大地间过渡电阻远远大于钢轨电阻,钢轨对地泄漏电流远远小于钢轨回流。站场牵引网结构布置如图1所示。

图1 站场结构布置示意图(单位:m)
1.1 测量方案
测试旨在测量当列车正常行驶经过上行侧预告信号机处绝缘节后,绝缘节2 侧4 条钢轨、上行侧吸上线及上下行侧横向连接线的回流情况。
预告信号机处现场布置如图2 所示。图中:Ia和Ib分别为上行区间侧的田野侧和线路侧钢轨电流;I2为下行侧的总回流;I3和I4分别为列车上行侧和下行侧的回流线回流;I5和I6分别为列车上行侧和下行侧的钢轨总回流;I7和I8分别为列车上行侧的田野侧和线路侧钢轨回流;I9和I10分别为列车下行侧的田野侧和线路侧钢轨回流。并且,Ia与Ib之和为牵引回流I;I5与I6之和为钢轨总回流Ir,I3与I4之和为回流线总回流Irl;I3与I5之和为上行侧总回流I1。

图2 预告信号机处现场布置示意图
测量方案:将电流传感器加装在预告信号机处上行侧的吸上线(图2 中蓝色线条)、钢轨连接扼流变压器的等阻线、上下行横向连接线(图2 中红色线条)上,电流传感器输出端通过探头连接至数据采集器,将数据采集器与电脑相连,即可完成测量线路布置。
1.2 测量数据
由于下行侧的总回流I2占总回流的比例很少,并且该站场实际情况复杂且测量设备有限,测量时只测上行侧各导线的回流。通过现场测试得到各线路回流电流的波形截图如图3所示。图中:CH1表示电流Ia;CH2 表示电流Ib;CH3 表示电流I7;CH4 表示电流I8;CH5 表示电流I3;CH6 表示电流I2。
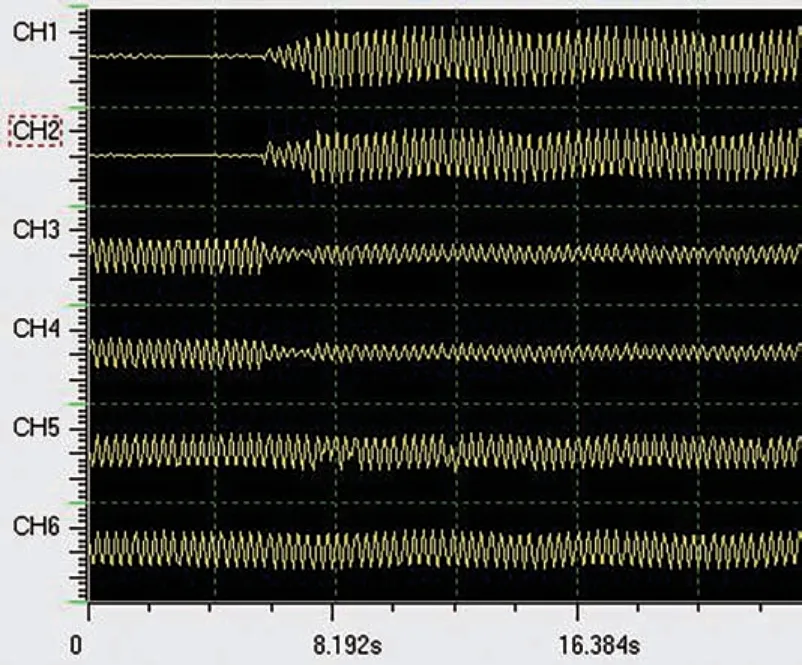
图3 各线路回流波形截图
根据图3 所示结果,计算得出所测的各导线回流占总牵引回流的分配比例系数如图4 所示。图中:上回为上行侧回流线的简称;上田轨为上行侧田野侧钢轨的简称;上线轨为上行侧线路侧钢轨的简称。同样的,下回、下田轨和下线轨为对应的简称。
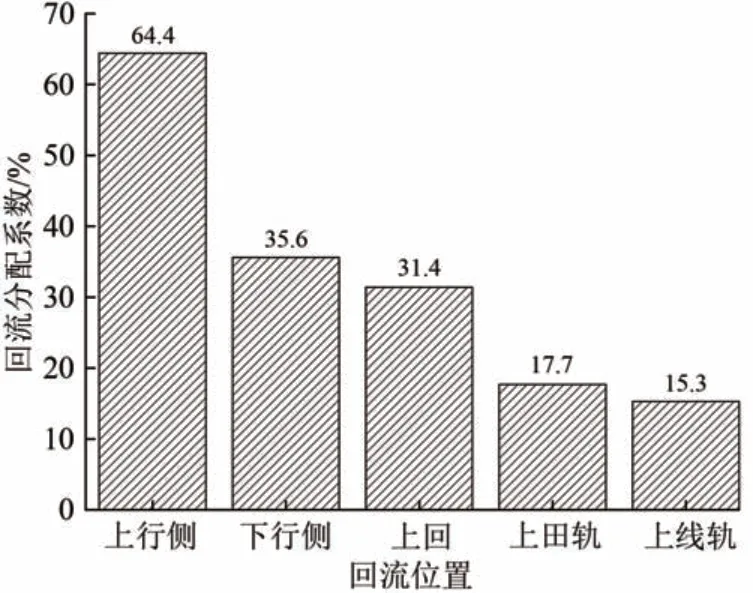
图4 实测回流分配比例系数
由图4 可见:列车上行侧牵引回流远大于下行侧回流;列车上行侧与下行侧的总回流之比为1.825∶1。
为了直观表示各导线回流分配情况,对各导线对应的回流分配系数做以下定义:各导线回流占牵引回流I的比例为回流分配系数P,Ir对应的回流分配系数为Pr,Irl对应的回流分配系数为Prl。同理,Ii(i=1,2,…,10)对应的回流分配系数为Pi。
此外,为明确表示各导线间回流分配情况,定义P1∶P2为列车上行侧与下行侧总回流之比,Pr∶Prl为钢轨总回流与回流线总回流之比,P3∶P8为列车上行侧回流线与下行侧回流线回流之比,P5∶P6为列车上行侧钢轨与下行侧钢轨回流之比,P7∶P8为列车上行侧田野侧钢轨与线路侧钢轨回流之比,P9∶P10为列车下行侧田野侧钢轨与线路侧钢轨回流之比。
由图4中实测结果得出,P3=31.4%,P7=17.8%,P8=15.4%,P2=35.6%。则P1∶P2=1.825∶1,P5∶P3=1.057∶1,P7∶P8=1.156∶1。
2 牵引回流系统仿真模型
2.1 模型基本参数
实测区间段的导线为:接触线、回流线、供电线与60 kg·m-1规格的钢轨。土壤类型选择均匀土壤,电阻率取沙质黏土的电阻率300 Ω·m,钢轨与大地的过渡电阻取15 Ω·km。具体线路参数见表1。
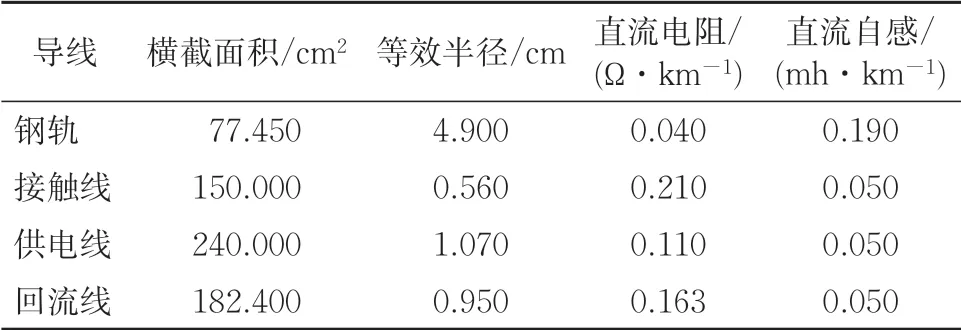
表1 线路参数
2.2 基础仿真模型
为了研究回流分配的机理及其影响因素,根据现场测试的预告信号机至进站信号机区间段的实际情况,采用EMTP 软件搭建不考虑各导线相互间耦合影响、仅考虑线路阻抗影响的基础仿真模型。该区间段的基础仿真模型如图5所示。
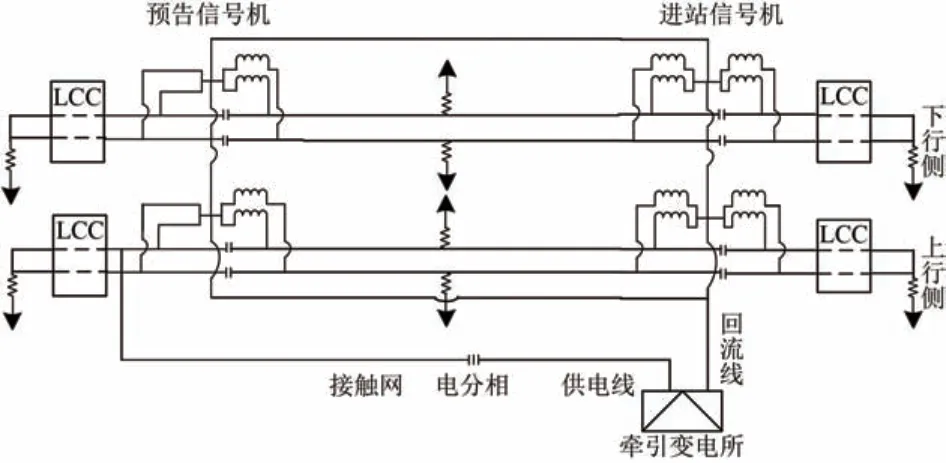
图5 基础仿真模型示意图
仿真模型中钢轨与大地间过渡电阻采用集中参数电阻等效代替,线路采用分布参数的LCC 模块。区间段外侧线路用1 km 的钢轨与4 个末端电阻等效代替[15]。牵引变电所位于站场上行线外侧中部,模型中用电流源等效代替。
2.3 考虑各导线相互影响的耦合仿真模型
基于基础仿真模型,分别仿真不考虑各导线间耦合影响,以及考虑钢轨、回流线、接触线和供电线相互间耦合影响,并采用比例法计算得出钢轨与回流线的回流分配系数如图6 所示。图中:白色框内为实测结果,其他颜色框均为仿真结果。
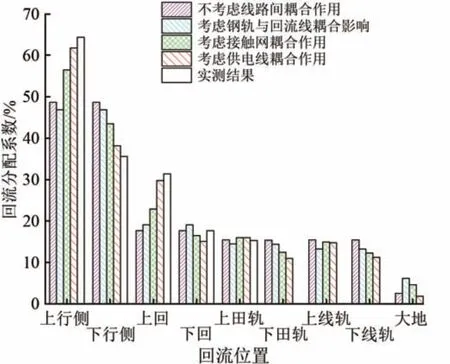
图6 回流分配系数仿真与实测对比
由图6可知:不考虑各导线相互间耦合影响时,列车上行侧与下行侧的总回流相等,P1∶P2=1,列车侧钢轨回流远大于回流线回流,P5∶P3=1.75,列车上行侧田野侧钢轨与线路侧钢轨回流相等,P7∶P8=1,且对比图4与图6(a)发现,不考虑各导线相互间耦合影响时,各导线的回流与实测相比差异很大,说明不考虑各导线相互间耦合影响的仿真模型是不正确的;考虑钢轨与回流线间耦合影响时,列车上行侧与下行侧的总回流仍相等,P1∶P2=1,列车侧钢轨回流仍远大于回流线回流,P5∶P3=1.46,列车上行侧田野侧钢轨回流略大于线路侧钢轨回流,P7∶P8=1.09;考虑钢轨、回流线、接触线相互间耦合影响后,列车上行侧回流大于下行侧回流,P1∶P2=1.3,列车上行侧钢轨回流大于回流线回流,P5∶P3=1.35,列车田野侧钢轨回流略大于线路侧钢轨回流,P7∶P8=1.07;考虑钢轨、回流线、接触线、供电线相互间耦合影响后,列车上行侧回流远大于下行侧回流,P1∶P2=1.70,列车上行侧钢轨回流略大于回流线回流,P5∶P3=1.03,列车田野侧钢轨回流略大于线路侧钢轨回流,P7∶P8=1.12。
综合以上仿真并对比实测结果发现,在考虑钢轨与回流线、接触线及供电线间耦合影响后,钢轨与回流线的回流分配系数非常接近实测结果,如列车上行侧回流线回流的仿真与实测误差为5.1%,故可以认为仿真所得导线间回流分配比例与实测所得导线间回流分配比例基本一致,因此计及钢轨与回流线、接触线及供电线相互间耦合影响的仿真模型是正确的。
3 回流分配影响因素
3.1 横向连接线的影响
设预告信号机与进站信号机区间段长为1 km,牵引变电所在进站信号机处,牵引电流通过接触线给区间段内列车供电。列车在上行侧行驶,牵引电流为1 000 A,采用考虑接触线、钢轨、回流线及供电线相互间耦合影响的仿真模型,分别仿真上下行侧有无横向连接线2 种情况下钢轨与回流线的回流分配比例,结果见表2。
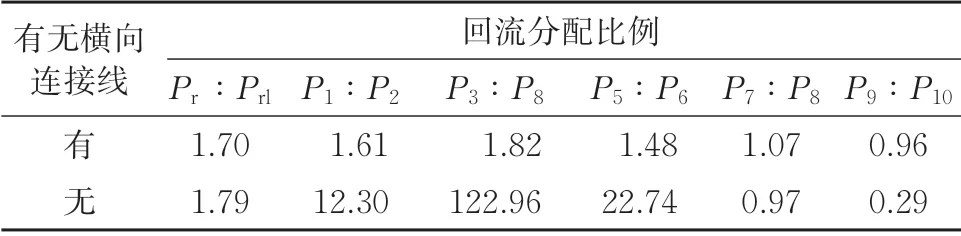
表2 横向连接线对回流分配比例的影响
由表2 可知:无横向连接线时,牵引回流通过列车上行侧钢轨回流,线路侧钢轨回流略大于田野侧钢轨回流,2 条钢轨回流之和为回流线回流的1.786 倍,下行侧线路产生耦合电流可以忽略不计;有横向连接线时,列车上行侧钢轨回流明显大于下行侧回流,列车上行侧田野侧钢轨回流略大于线路侧钢轨回流。
3.2 接触线长度的影响
在列车行驶过程中,随着列车位置的变化,牵引电流流经接触线的长度是变化的,钢轨与回流线的回流距离也是变化的。设列车在上行侧行驶,牵引电流为1 000 A,上下行钢轨间距为5 m,分别仿真上下行侧钢轨间有无横向连接线时,接触线长度从0.1~10.0 km变化时线路的回流分配情况。
3.2.1 无横向连接线时
仿真上下行钢轨间没有横向连接线、接触线长度从0.1~10.0 km 变化时,列车上行侧各导线回流分配比例如图7。
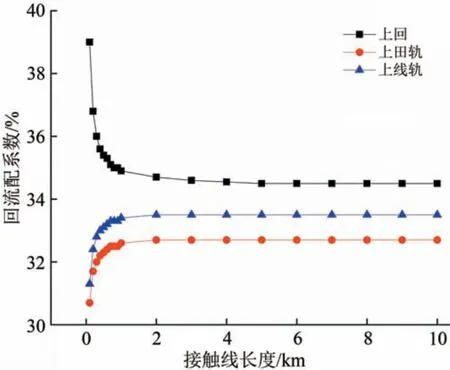
图7 无横向连接线时接触线长度对回流分配系数影响
由图7 可知:当接触线长度在0.1~1.0 km 内变化时,列车上行侧回流线回流明显减小,钢轨回流明显增大;当接触线长度在1~3 km 内变化时,回流线回流略微减小,钢轨回流略微增长;当接触线长度大于3 km 时,钢轨与回流线回流基本保持不变。
计算得出对应线路间的回流分配比例见表3。
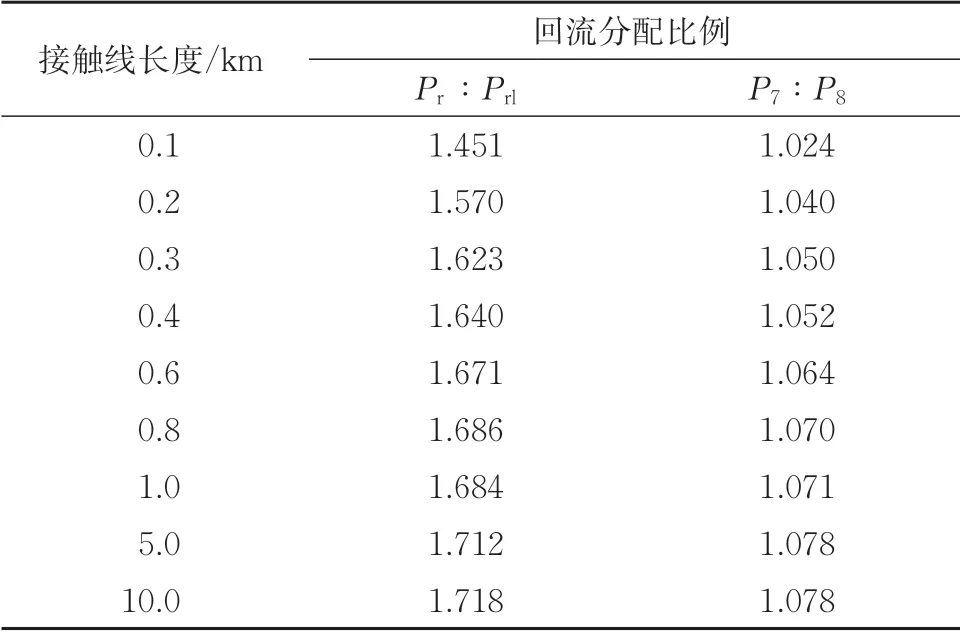
表3 无横向连接线时接触线长度对回流分配比例的影响
3.2.2 有横向连接线时
仿真上下行钢轨间有横向连接线、接触线长度从0.1~10.0 km 变化时,各导线回流分配比例如图8所示。
由图8 可知:列车在上行侧行驶时,受接触线耦合作用影响,列车上行侧的各导线回流均大于下行侧各导线回流;当接触线长度在0.1~1.0 km 内变化时,列车上行侧钢轨与回流线的回流明显减小,下行侧钢轨与回流线回流明显增大;当接触线长度在1~3 km 内变化时,钢轨与回流线的回流变化很小;当接触线长度大于3 km 时,钢轨与回流线的回流基本保持不变。
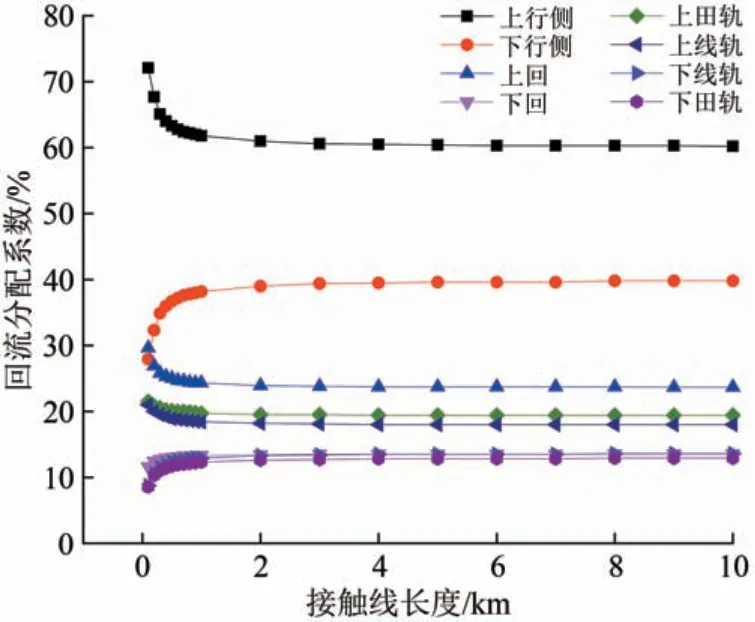
图8 有横向连接线时接触线长度对回流分配系数影响
计算得出对应线路间回流分配比例见表4。

表4 有横向连接线时接触线长度对回流分配比例的影响
3.3 上下行钢轨间距的影响
上下行钢轨间没有横线连接线时,上下行钢轨间距变化对回流分配比例没有影响。设上下行线路有横向连接线,列车在上行侧行驶,牵引电流为1 000 A,接触线长度为5 km,仿真上下行钢轨间距从5~100 m 变化时,各导线回流分配系数变化情况如图9所示。

图9 有横向连接线时上下行钢轨间距对回流分配系数影响
由图9 所知:随着上下行钢轨间距从5 m 逐渐增大为100 m,接触线对下行侧线路的耦合作用逐渐减小,使得列车上行侧各导线回流逐渐增大,下行侧各导线回流逐渐减小;当上下行钢轨间距小于50 m 时各导线回流变化较为明显,而大于50 m 时变化缓慢,逐渐趋于1个固定值。
选取上下行钢轨间距变化过程中的关键点,计算得出对应线路间的回流分配比例见表5。
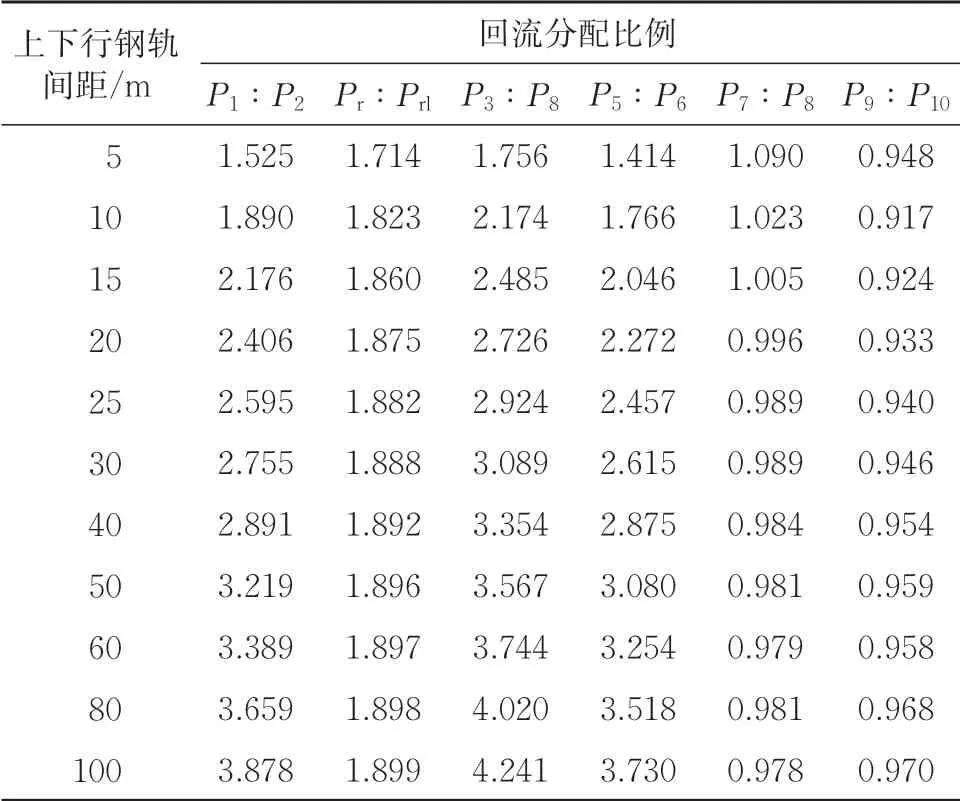
表5 有横向连接线时上下行钢轨间距对回流分配比例的影响
通过以上分析,表3 中的数据,用于估算直接供电方式下没有铺设贯通地线且上下行钢轨没有横向连接线的站场基本供电区间段的牵引回流分配情况;表4 和5 中的数据,用于估算直接供电方式下没有铺设贯通地线且上下行钢轨有横向连接线的站场基本供电区间段的牵引回流分配情况。
4 应用实例
根据上述表格中得到的牵引回流分配比例数据,推导出各导线回流电流的计算式为
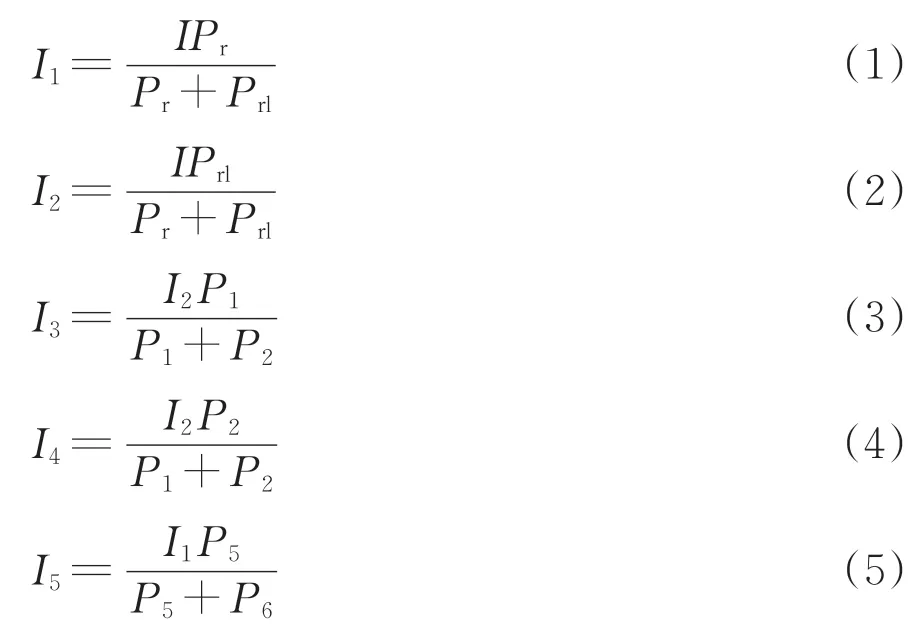

为了验证所推导计算式的正确性,设某站场供电方式为带回流线的直接供电方式,站场预告信号机与进站信号机处上下行侧的扼流变压器通过横向连接线相连,接触线长度为3 km,上下行钢轨间距为25 m,站场没有铺设综合地线,牵引网结构有接触线、钢轨与回流线。牵引电流为300 A 时列车从站场驶出经过上行侧预告信号机,同时在下行侧牵引电流为500 A 时列车向站场方向行驶至预告信号机处,分别采用计算法与仿真模型得出此时各导线的回流电流。
为方便计算说明,定义Kx-y为接触线长度为x km 且上下行钢轨间距为y m 时各导线的回流分配比例系数。
查表4 发现没有接触线长3 km 时导线的回流分配比例,则采用均值法计算得出,为

表5 中数据为接触线长度为5 km 时求出的,则采用差值法估算得出接触线长度为3 km、上下行钢轨间距为25 m时各导线的回流分配比例为

采用式(1)—式(10)计算上行侧牵引电流为300 A 的列车驶过时,各导线回流电流为:I3=78.25 A,I4=26.43 A,I7=68.90 A,I8=70.77 A,I9=27.00 A,I10=28.65 A。
当下行侧牵引电流为500 A 的列车驶过时,计算各导线回流电流得:I4=130.42 A,I3=44.05 A,I9=114.83 A,I10=117.95 A,I7=45.00 A,I8=47.75 A。
采用叠加法,将2 次计算结果叠加得:I3=122.30 A, I4=156.85 A, I7=113.90 A, I8=118.52 A,I9=141.83 A,I10=146.60 A。
为验证计算法得出的各导线回流是正确的,采用章节2.3中的考虑接触线、钢轨、回流线及供电线相互间耦合影响的仿真模型。此外,在第3节中已经验证了该仿真模型与实测结果的最大误差为5.1%,故可用仿真结果代替实测结果对计算法验证。因此,按照实例设定条件进行仿真,得到各导线回流电流为:I3=123.7 A,I4=156.5 A,I7=116.8 A,I8=120.4 A,I9=143.2 A,I10=146.1 A。
将仿真结果与计算结果对比,如图10所示。
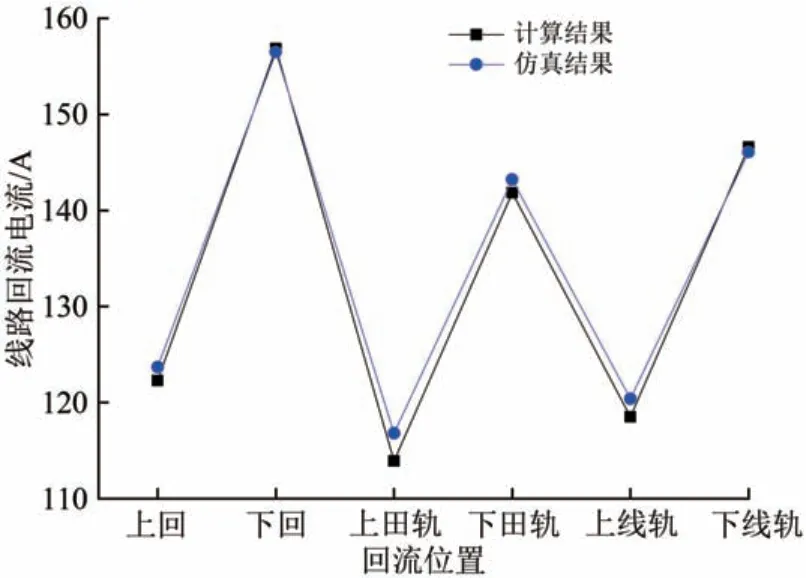
图10 计算与仿真结果对比
由图10 可见:计算结果与仿真结果基本一致,但是由于耦合地线的影响,造成实测结果比计算结果偏大;二者上行田野侧钢轨电流差最大,误差为2.48%,则可以认为采用计算法得出的线路回流与实测结果的误差小于10%,即上述线路回流的估算方法是正确的。
5 结 论
(1)通过仿真与实测结果的对比研究,发现仅考虑阻抗影响或仅考虑钢轨与回流线耦合作用的仿真结果与实测结果存在差异,考虑钢轨与回流线、接触线及供电线相互间耦合影响的仿真模型的仿真结果与实测结果一致。
(2)研究了各导线之间的耦合作用对回流分配比例的影响,发现考虑接触线、供电线、钢轨、回流线相互间耦合影响对线牵引回流分配起决定性作用。如仅考虑钢轨与回流线间耦合作用时,P1∶P2=1;考虑接触线、供电线、钢轨、回流线相互间耦合影响作用时,P1∶P2=1.7。
(3)研究发现各导线间耦合作用是造成钢轨不平衡电流的主要原因。上下行钢轨没有横向连接线时,上行线路侧钢轨回流大于田野侧钢轨回流;上下行钢轨间有横向连接线时,列车上行侧田野侧钢轨回流大于线路侧钢轨回流,列车下行侧两条钢轨回流相差不大。
(4)研究给出了接触线长度、上下行钢轨间距变化时区间段内牵引回流分配比例,并根据不同导线间的比例关系,提出了一种工程估算区间段内各导线回流电流的方法,并通过实例进行了仿真验证。
