圆柱壳大开孔接管连接处弯曲应力性质和评定准则的探讨及论证

左安达

（惠生工程（中国）有限公司，上海 201210）

压力容器圆柱壳开孔接管的补强设计一直是国内外长期以来都没有很好解决的一个问题，原因在于壳体和接管连接处应力产生的原因和性质较为复杂，不同原因引起的应力性质不同，对结构造成的危害程度和失效模式亦不同，尤其对于开孔率较大的大开孔接管，开孔边缘的应力会大大增加且难以区分其性质，因此对于开孔区的补强设计须区别对待，选取合适的补强方法才能保证计算的准确性和设计的安全性。工程设计中常用的一种方法是采用有限元计算，基于应力分类法对不同性质和危害程度的应力加以划类，分别按不同的准则区别评定，以保证结构设计的安全性，应力分类法在原理和定义上是清晰明确的，但具体怎么划类则带有经验性和人为因素的影响，比如对于上述壳体大开孔接管连接处产生的薄膜应力和弯曲应力既有一次应力成分也有二次应力成分，但目前所有主流的有限元软件计算等效线性化的结果仅能区分出是均匀分布的薄膜应力还是线性分布的弯曲应力，而无法进一步区分出一次或二次性质。根据应力分类法的评定原则，对由薄膜应力、弯曲应力和峰值应力构成的SⅠ、SⅡ、SⅢ、SⅣ、SⅤ应逐级进行评定，但是对于弯曲应力，按以往的经验若将其归类为SⅢ进行评定，此时是安全的但被指过于保守，若将其归类为SⅣ进行评定，则设计又会趋于不安全，保守程度和不安全程度跟开孔率亦是有着直接关系[1]。基于上述的理解，进行开孔接管结构合理设计的必要条件有两点：一是需要对壳体大开孔接管连接处弯曲应力的性质进行更为准确的判定；二是需要采取更为准确的评定准则来保证设计既安全又不至于太保守。本文基于有限元计算及应力分类的原理，对圆柱壳大开孔接管连接处弯曲应力的性质及评定准则进行探讨、对比验证和归纳总结，以期能够为工程应用提供一定的参考价值和设计依据。

1 圆柱壳大开孔接管连接处弯曲应力性质的探讨及论证

1.1 弯曲应力产生的原因探讨

基于国内、外学者长期大量的研究工作，对圆柱壳大开孔接管连接处弯曲应力在内压作用下产生的原因逐渐有了进一步的认识，主要有四种观点：观点一认为当壳体接管开孔率较小时，孔边缘只有薄膜应力而无弯曲应力，而开孔率较大后（＞0.5），接管开孔会跨越较大的筒体圆周，使开孔位于“曲板”上，受圆筒曲率的影响会产生很大的弯曲应力，故称为“圆筒曲率影响”观点；观点二认为由于壳体和接管在载荷作用下自由变形不同，为满足变形协调而产生的弯曲应力，即“变形协调”观点；观点三首次见诸ASME Ⅷ-1—2004 版，认为壳体大开孔接管区域破坏了开孔区的轴对称性，使得内压作用状态发生变化引起沿圆筒方向的环向弯矩并产生弯曲应力，且明确了此弯曲应力为一次应力，称之为“静力平衡”观点[2]；观点四是根据有限元分析结果所揭示的孔边缘应力分布情况并由国内学者提出的，该观点认为开孔边缘不仅有ASME 指出的绕圆筒母线方向的环向弯矩，同时还存在与该弯矩正交的、数量级相当的绕接管母线方向的另一弯矩，且进一步的研究表明此弯曲应力也为一次应力并沿接管（或筒体）环向，称之为“等值拉压开孔平板孔边弯曲应力” 观点[3]。其中，前三种观点已被广泛认可并见诸各种相关标准和释义中，观点四仅在个别研究文献中被提及，目前在行业内还未得到更为广泛的认识。

如上所述，观点四是基于有限元计算分布云图得出的观点，并得到国内学者进一步的研究和论证，其核心观点及论据主要有三点：

（1）由图1 应力分布云图和等值线图可直观看出，圆柱壳与接管连接区“肩部”截面的应力等值线始终与壳体轴线呈现出约45°的倾斜分布趋势，表明开孔边缘不仅有ASME 所指出的绕圆筒母线方向的环向弯矩，同时必然还存在另一个与之相正交的弯矩，否则应力等值线不可能呈现45°倾斜分布趋势；

图1 应力分布云图和等值线图Fig.1 Stress distribution and contour graph

（2）由图2 接管和圆筒变形示意图可直观看出，圆筒上接管部位的形状由圆趋扁，表明ASME 中提出的绕圆筒母线方向弯矩的存在；圆柱壳与接管的相贯线由圆形变成了椭圆形，表明开孔边缘同时存在着绕接管母线方向的弯矩，该弯矩产生的应力沿接管环向（在开孔肩部处亦为圆筒环向）；

图2 接管和圆筒变形示意图Fig.2 Schematic diagram of pipe and cylinder deformation

（3）清华大学陆明万教授的文章[4]对图1 的变形情况给出了理论解释，认为由于圆柱壳环向薄膜应力比轴向大一倍，使得补强环出现由均匀拉伸和等值拉压组合而成的非轴对称受力情况，才导致出现了环平面内由圆形变为椭圆形的弯曲变形，进而产生了绕接管母线方向的弯矩，并推导出该弯矩值为pR3/8，与ASME 的环向弯矩pR3/6 数量级相当，产生的原因亦与ASME 弯矩相似，因轴对称性被破坏而产生的弯矩，因而其引起的弯曲应力具有一次应力性质。

综上所述，内压作用下圆柱壳大开孔接管开孔边缘处弯曲应力产生的原因、方向和性质按目前国内外的研究成果可归纳总结如下：

（1）“圆筒曲率影响”观点和“变形协调”观点认为的弯曲应力，方向为沿圆筒或接管轴向，性质为二次应力，此两种观点已被广泛研究和认可；

（2）ASME 标准中“静力平衡”观点认为的弯曲应力，方向为沿圆筒环向，性质为一次应力，但仅计及了绕圆筒方向的弯矩作用；

（3）“等值拉压开孔平板孔边弯曲应力”观点认为的弯曲应力，方向为沿接管环向（在开孔肩部处亦为圆筒环向），性质为一次应力，该观点还未得到广泛的认识且未见诸相关标准中。

上述四种观点在开孔边缘处产生的弯曲应力是同时存在且相互叠加或抵减的，共同组成了既有一次成分又有二次成分的总弯曲应力（为后续表述方便，将观点一、二简称为由变形协调引起，观点三、四简称为由静力弯矩引起）。

1.2 弯曲应力性质的进一步探讨和论证

准确认识和判定开孔边缘处弯曲应力性质对于采用应力分类法进行强度评定是至关重要的，有限元软件等效线性化后的结果仅能给出弯曲应力的总值，并不能进一步区分出一次弯曲应力值和二次弯曲应力值的大小。但根据前文及文献 [3]所述，由不同原因产生的弯曲应力的方向和性质是明确而清晰的，因此便提出一种方法，可根据有限元计算结果中应力的方向和数值大小来判定弯曲应力的性质及比重：一次成分占主导或是二次成分占主导。本文忽略其他因素的影响，仅考虑开孔率单一因素，采用有限元软件对开孔率ρ= 0.1 ～ 0.9 的某一系列圆柱壳开孔接管模型分别进行了计算，来进一步验证上述判别方法的可靠性及弯曲应力的性质[5]。限于文章篇幅有限，文中仅列出开孔率ρ= 0.7 时肩部截面最大应力点处的总应力、环向、轴向、径向应力分布云图，如图3 所示。

图3 肩部截面应力分布云图Fig.3 Graph of stress distribution on shoulder section

由图3 对比发现：环向应力分布云图3b 和总应力分布云图3a 不仅应力分布云纹线极其相似，且数值也极为接近（仅相差0.6%），最大应力点处环向应力和总应力值分别为814.06 MPa 和819 MPa（仅相差0.6%），另外轴向应力和径向应力极小且为负值，表明该处总应力主要是由环向应力决定的，且可根据前文判断出构成此环向应力的弯曲成分性质应属于一次应力。

为进一步验证，本文又从其他角度进行了分析，根据有限元计算结果提取了开孔率ρ= 0.1 ～ 0.9 时有限元模型计算的环向应力和总应力值，并通过最大应力点法向路径上线性化后的弯曲应力值并绘制成曲线如图4a、4b 所示。

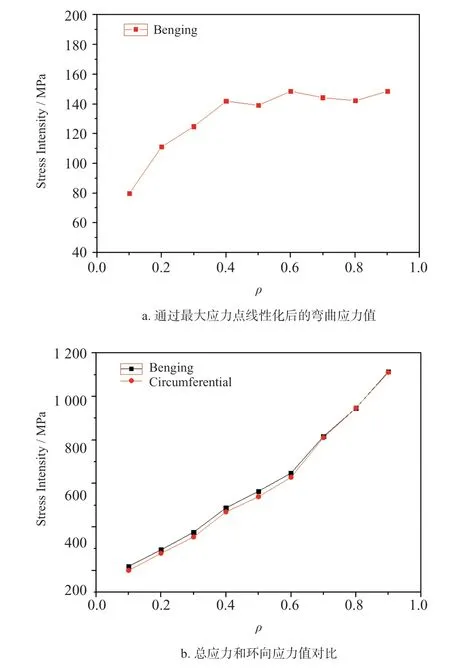
图4 开孔率ρ = 0.1 ～ 0.9 时总应力、环向应力及线性化后的弯曲应力值Fig.4 The total stress, hoop stress and linearized bending stress at the opening rate ρ = 0.1 ～ 0.9

由图4a 可直观看出：当开孔率ρ＜0.5 时，随开孔率的增大，弯曲应力值呈单调递增的变化趋势，且增加幅度较为明显；当开孔率ρ＞0.5 后，随开孔率的增大，弯曲应力值呈现出或增或减的无规律变化，但应力值变化幅度很小。从理论上分析：开孔率越大，开孔区非轴对称性越严重，则由静力弯矩引起的一次弯曲应力势必增大，但同时接管与壳体的刚度比变小，变形协调性趋于缓和，为满足变形协调产生的二次弯曲应力应减小。故当开孔率ρ＜0.5 时，随开孔率的增大，连接处由静力弯矩引起的一次弯曲应力必然增大，变形协调引起的二次弯曲应力理应减小，而总弯曲应力却显著增加，只能表明一次弯曲应力增幅较大，二次弯曲应力减幅较小，才会使得总弯曲应力显著增加；当开孔率ρ＞0.5 时，随开孔率的增大，由静力弯矩引起的一次弯曲应力必然也是逐渐增大的，而总弯曲应力却变化不明显甚至下降，只能表明由变形协调引起的二次弯曲应力逐渐减小且减幅显著增大。通过上述分析可判断出：对于开孔率较大的大开孔接管，连接处弯曲应力一次成分显著增大，二次成分显著减小，一次弯曲应力所占比重较大占主导作用，且开孔率越大，一次成分占比也越大。

由图4b 对比分析：随开孔率的增大，环向应力在总应力中的占比逐渐增大，尤其当开孔率ρ＞0.7后，总应力几乎全是由环向应力构成的，进一步表明圆柱壳大开孔接管连接处的弯曲应力主要是环向的一次弯曲应力。仍需说明的是，上述分析均是建立在以开孔率为单一因素的考量上，理论上一次弯曲应力占比究竟有多大，还与承受的载荷大小、接管与壳体刚度比等因素有关。

2 圆柱壳大开孔接管连接处弯曲应力评定准则的探讨

2.1 基于应力分类法弯曲应力评定准则的探讨

根据应力分类法的评定原则，对由薄膜应力、弯曲应力构成的SⅠ、SⅡ、SⅢ、SⅣ应逐级进行评定，当有疲劳问题时，还需对峰值应力强度SⅤ进行评定。但是多年来由于圆柱壳开孔接管连接处弯曲应力性质的难以判定，我国工程设计人员在对弯曲应力进行评定时所采用的准则也不统一，一种常见的做法是将弯曲应力全部归类为二次应力，采用SⅣ＜3.0Sm进行评定，直接忽略SⅢ不评定，这种做法并不符合标准逐级评定的要求，更重要的是本文分析表明对于大开孔接管连接处弯曲应力成分主要为一次应力，那么仅按SⅣ评定而漏评SⅢ就是不正确的，同时也明显存在着很大的不安全性。按标准要求则应严格按SⅢ＜1.5Sm进行评定，此时是安全的但又被指过于保守，以往认为保守的原因主要是：总弯曲应力中既有一次成分又有二次成分，而按SⅢ评定则是将其全部归类为一次弯曲应力，故保守。但基于本文的分析，对于小开孔接管连接处二次弯曲应力在总应力中占比也较大，可能会存在保守的问题；对于大开孔接管连接处则主要是一次弯曲应力，那么保守程度就大大降低了，故对于圆柱壳大开孔接管连接处弯曲应力的评定按SⅢ＜1.5Sm评定符合标准要求[6-7]。

2.2 弯曲应力评定准则的进一步探讨和论证

SⅢ＜1.5Sm的理论基础是根据矩形截面梁纯弯曲条件下的弯曲应力分布及极限载荷分析而得来，因初屈服载荷（弹性极限载荷）与塑性极限载荷之间有个应力重分布的过程，可进一步发挥低应力区的承载潜力，并将由此得来的承载潜力系数1.5 引入到应力分类法中对于SⅢ的评定准则中，并经多年实践经验表明对于绝大多数结构是安全可靠的，但是对于一些结构来说，又显得过于保守。对于本文所探讨的圆柱壳大开孔接管连接处存在两个特殊的截面（如图2 所示）：沿筒体轴线方向的截面，称为开孔结构的“肩部”截面；沿筒体环向的截面，称为开孔结构的“腰部”截面。在内压作用下，最大总应力点首先出现在肩部截面接管根部（如图1 所示），由静力弯矩引起的一次弯曲应力最大应力点也始于该处，随着内压的增大，当达到屈服强度时，该最大应力点最先屈服，随后屈服区域不断扩大直至整个“肩部”截面全部屈服达到承载极限，但因其他截面尚未屈服，故整个开孔结构并未完全失效且仍有较大的承载能力，当压力继续增大时，会发生应力沿接管与壳体相贯线重分布的过程，只有当屈服区域由“肩部”截面扩展到“腰部”截面后，整个开孔结构才完全丧失承载能力而失效[8]。

因而，圆柱壳大开孔接管结构存在两个应力重分布过程：一是由接管根部最大应力点向整个“肩部”截面的应力重分布过程；二是由“肩部”截面沿接管与壳体相贯线向“腰部”截面的应力重分布过程；而对于矩形截面梁，只存在沿截面上、下表面向中间截面的应力重分布过程。两者应力重分布的过程不同，承载能力也必然不同：首先，“肩部”和“腰部”截面是壳体和接管的组合截面（类似于角钢截面），其承载能力必然大于单一的矩形截面；其次，开孔接管结构比矩形截面梁多出一个沿相贯线的应力重分布过程。因此，圆柱壳大开孔接管结构的承载潜力必然远大于矩形截面梁，那么按矩形截面梁的承载潜力系数1.5 来评定大开孔接管结构，显然会造成过于保守的结果。通过上述分析可知，圆柱壳大开孔接管连接处弯曲应力的评定若按SⅣ＜3.0Sm，则会存在很大的不安全性，若按SⅢ＜1.5Sm评定会过于保守。为更好地验证，本文对开孔率ρ=0.5 ～ 0.9 的模型做了进一步的极限载荷分析，并将其计算结果与应力分类法采用SⅢ＜1.5Sm、SⅣ＜3.0Sm的评定结果进行了对比，如表1 所示。

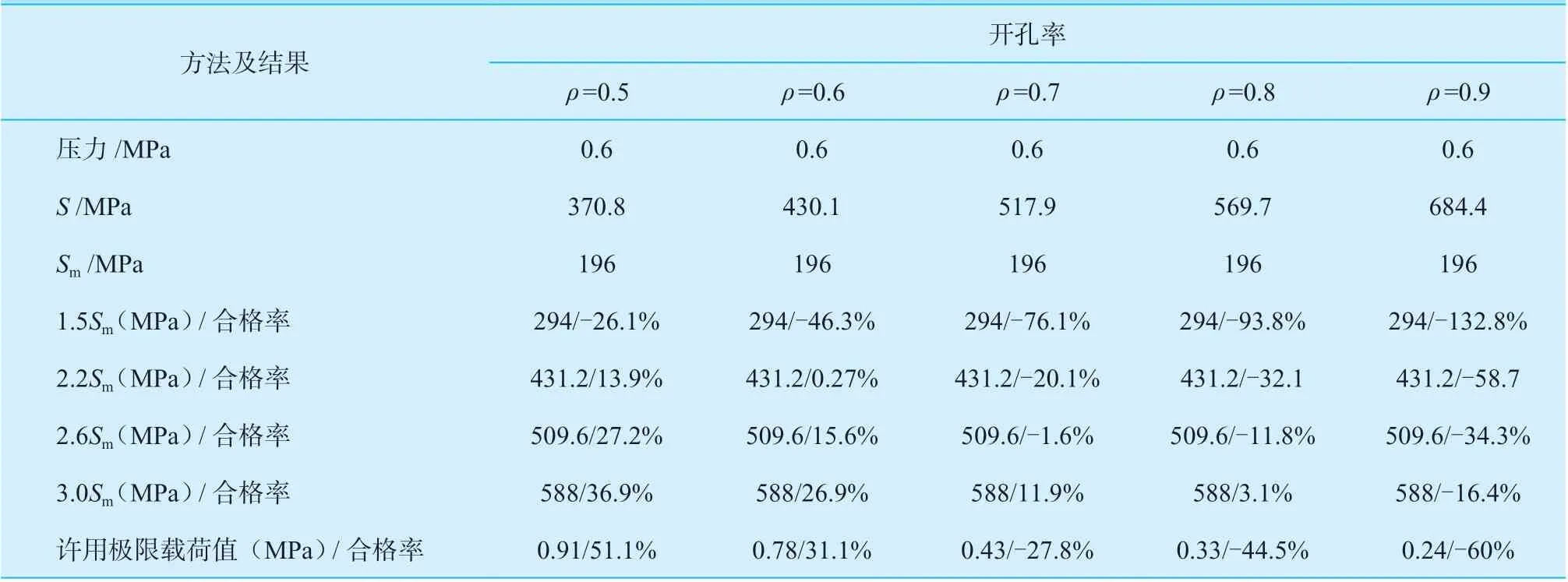
表1 极限载荷计算结果与应力分类法评定准则对比Table 1 Comparative discussion between limit load analysis and evaluation criteria based on stress classification method

极限载荷分析体现了开孔接管结构在压力作用下的应力重分布过程，考虑了整体结构的极限承载能力，可作为对比验证的依据[9-12]。根据表1 结果，通过极限载荷分析和弹性应力分类法的评定准则对比分析：开孔率ρ=0.5 ～ 0.9 时，按SⅢ＜1.5Sm准则评定结果均不合格，不合格率为-132.8% ～ -26.1%，而许用极限载荷在开孔率ρ=0.5 ～ 0.6 评定结果均是合格的，在开孔率ρ=0.7 ～ 0.8 时虽然不合格，但不合格率的数值远小于按1.5Sm评定的结果，表明按SⅢ＜1.5Sm准则对圆柱壳大开孔接管结构评定结果是过于保守的。若按SⅣ＜3.0Sm准则进行评定，则开孔率ρ=0.5 ～ 0.8 时评定结果均是合格的，而许用极限载荷在开孔率ρ=0.5 ～ 0.6 时评定结果是合格的，从合格率数值对比表明，此开孔率下按3.0Sm评定比极限载荷评定更为严格、安全性是可靠的；但是当开孔率ρ=0.7 ～ 0.9 时许用极限载荷评定结果则均是不合格的，从图5 可看出，随开孔率ρ的增大，结构的极限载荷值降低显著，即承载能力下降很快，对比表明此开孔率下按SⅣ＜3.0Sm准则对圆柱壳大开孔接管结构评定会存在很大的不安全性。

图5 开孔率 ρ =0.1 ～ 0.9 时极限载荷变化趋势Fig.5 The changing trend of the limit load when the opening rate ρ =0.1 ～ 0.9

综上章节1、2 所述，对于圆柱壳大开孔接管结构连接处弯曲应力应按一次弯曲应力考虑，评定准则应按应力分类法中的SⅢ进行评定，但承载潜力系数应是介于1.5 ～ 3.0 之间的某一个数值，此数值与开孔率、接管与壳体刚度比等因素都有直接关系，因而不可能有同一个数值能够保证不同开孔率下均具有相同的安全裕度，但又必须取统一的数值以方便于工程应用（如表1 中对不同的开孔率按统一的3.0Sm评定，在ρ=0.5 ～ 0.6 时安全能够保证且具有一定余量，而ρ=0.7 ～ 0.9 时却不能保证安全性）。国内清华大学基于塑性极限分析与试验研究的开孔补强分析法和圆柱壳开孔接管应力分析法中便将一次应力SⅡ准则的系数由1.5 调整为2.2，以改善保守程度；将一次+二次应力SⅣ准则的系数由3.0 调整为2.6，以提高安全裕度。表1 中也将按2.6Sm和2.2Sm准则评定的结果与极限载荷分析结果作了对比：可看出在开孔率ρ=0.5 ～ 0.6 时，按2.6Sm和许用极限载荷评定结果均合格，但ρ=0.7 ～ 0.9 时，虽然评定结果均合格，但对比不合格率的数值可看出按2.6Sm安全裕度似乎也不够，对于特大开孔率的结构仍有不安全的可能性；按2.2Sm评定，ρ=0.7 ～ 0.9 时不合格率的数值与许用极限载荷评定结果更为接近，另外许用极限载荷的取值还有1.5 的安全系数，有一定的安全裕度。通过上述一系列的对比验证，可综合判断出将圆柱壳大开孔接管结构连接处的弯曲应力划类为一次弯曲应力并将承载潜力系数由1.5 调整为2.2 按SⅢ＜2.2Sm进行评定，似乎是一个更为折中合理的选择，既能保证特大开孔率结构的安全性又能降低较小开孔率结构的保守程度。

4 结论

本文基于有限元软件对某一系列开孔率的圆柱壳大开孔接管结构进行了计算，通过应力云图、线性化后的应力变化规律、极限载荷计算结果并结合理论分析对其连接处弯曲应力的性质和评定准则进行了探讨、对比验证和归纳总结，得出以下若干结论和建 议：

（1）对于圆柱壳大开孔接管结构，在开孔边缘处不仅有ASME 指出的绕圆筒母线方向的环向弯矩，同时还存在与该弯矩正交的、数量级相当的绕接管母线方向的另一弯矩，两个方向的弯矩会引起很大的弯曲应力。

（2）对于开孔率较大的（尤其是ρ＞0.5 后）大开孔接管与壳体连接处由静力弯矩引起的一次弯曲应力成分显著增大，由变形协调引起的二次弯曲应力成分则显著减小，一次弯曲应力为主要成分占主导作用，且开孔率越大，一次弯曲应力成分占比也越大。故归类为SⅢ进行评定更为合理，不能归类于SⅣ进行评定，否则漏评了SⅢ，不符合应力逐级评定的要求，同时把一次应力按二次应力评定会出现很大的不安全性。

（3）圆柱壳大开孔接管结构存在两个应力重分布过程，比矩形截面梁多出一个沿相贯线的应力重分布过程，承载能力远大于矩形截面梁。故分析设计标准中关于一次应力的评定准则SⅢ＜1.5Sm中承载潜力系数1.5 用于圆柱壳大开孔接管连接处会造成过于保守的评定结果。

（4）通过极限载荷计算结果与应力分类法的对比分析表明：圆柱壳大开孔接管连接处弯曲应力，若按SⅢ＜1.5Sm进行评定，对大开孔率结构确实会存在过于保守的结果；若按SⅣ＜3.0Sm进行评定，确实也会存在不安全的风险。

（5）基于国内学者的研究成果和进一步的对比验证，认为将圆柱壳大开孔接管结构连接处的弯曲应力归类为一次弯曲应力并将承载潜力系数由1.5 调整为2.2 进行评定似乎是一个更为折中合理的选择，既能保证特大开孔率结构的安全性又能降低较小开孔率结构的保守程度。故建议在工程设计中，可按SⅢ＜2.2Sm进行评定，作为一种辅助的评定准则，以更进一步的自我评估，设计出更为安全、合理、经济的结构。

（6）本文是建立在前辈研究的基础上并结合个人理解提出的观点和建议，文中观点还需要更多、更进一步的实验研究、数值分析和工程实际应用案例的对比验证。有限元应力分析设计理念自引入国内已有30 ～ 40 年应用，但在很多工程实际应用中，分析设计似乎成为了常规设计的一种校核、验证的辅助设计方法，往往并没有体现出分析设计这一先进方法的优越性。期待随着国内外学者的不断研究和新方法的不断引进，分析设计能真正为工程设计带来更大的改变和突破，将其先进理念得到更进一步的体现和发挥。