鼓形修形和偏载对直齿轮强度的影响研究*

2018-11-27夏建芳

机电工程 2018年11期

曹然，夏建芳

(中南大学机电工程学院，湖南长沙 410083)

0 引言

在工程应用中，由于加工误差、安装误差、轴承变形以及齿轮本身的扭转变形等，均会对齿轮啮合过程的振动、噪音以及强度等产生重要的影响[1,2]。

LI等[3]通过一系列实验研究了鼓形修形和安装误差对直齿圆柱齿轮啮合强度的影响，结果表明鼓形修形和安装误差会增大齿面接触应力和齿根弯曲应力；TRAN等[4-5]通过实验研究了加工误差对齿轮接触强度的影响，结果表明齿面接触应力随着加工误差的增加而增大；LITVIN等[6]在前人的基础上通过有限单元法研究了齿轮的加工误差、安装误差和修形与齿轮的静态传递误差、啮合刚度和载荷分配比之间的关系，结果表明齿轮的加工误差、安装误差和修形均会影响齿轮的静态传递误差、啮合刚度和载荷分配比，加工误差会改变静态传递误差曲线的形状，而安装误差和修形不会；罗才旺[7]通过Romax软件计算得到了齿轮静态传递误差，建立了齿轮系统方程，并用该方程研究了平行度误差、载荷和修形对齿轮动态传递误差和动载系数的影响规律。

齿轮传动系统运转过程中，因传动轴在载荷作用下发生弯曲变形，或因传动轴、齿轮副安装过程产生安装误差，导致直齿轮沿齿宽产生边缘接触，造成载荷在齿宽方向分配不均匀，引起齿宽边缘应力集中，即“偏载现象”。

本文将以直齿圆柱齿轮为研究对象，研究修形和偏载对齿轮齿面接触强度和齿根弯曲强度的大小和分布情况的影响。

1 初始模型建立和分析

1.1 模型的建立

直齿圆柱齿轮副模型的几何参数如表1所示。

表1 齿轮副几何参数

本研究由表1中参数构出齿轮的三维模型，并通过Abaqus对其进行网格划分。

网格划分后的有限元模型及其在有限元分析中的边界条件等情况如图1所示。

图1 齿轮副边界条件示意图

1.2 边界条件的设定

本研究在分析前调整齿轮之间的装配位置，保证大小轮两端面之间的距离相等，然后在两个齿轮中心分别创建节点O1和O2，并在O1和O2上分别创建相应的局部坐标系，然后将O1和O2与它们对应的齿轮的内圈耦合。

根据LI[8]的分析模型，本研究给大轮耦合节点O1施加大小为0.85 rad的角位移，在Abaqus中的时间步长设置为0.005，保证两齿轮始终在细网格之间啮合，给小轮耦合参考点O2施加大小为100 N·m的负载转矩，以此来模拟齿轮副运转的实际工况。

1.3 结果分析

通过上述分析得到的大轮齿面接触应力和齿根弯曲应力的分布情况如图2所示。

图2 接触应力和弯曲应力分布情况

齿面接触应力和齿根弯曲应力在单齿啮合最高点出现最大值，该位置接触应力和弯曲应力沿齿宽方向的大小和分布情况如图3所示。

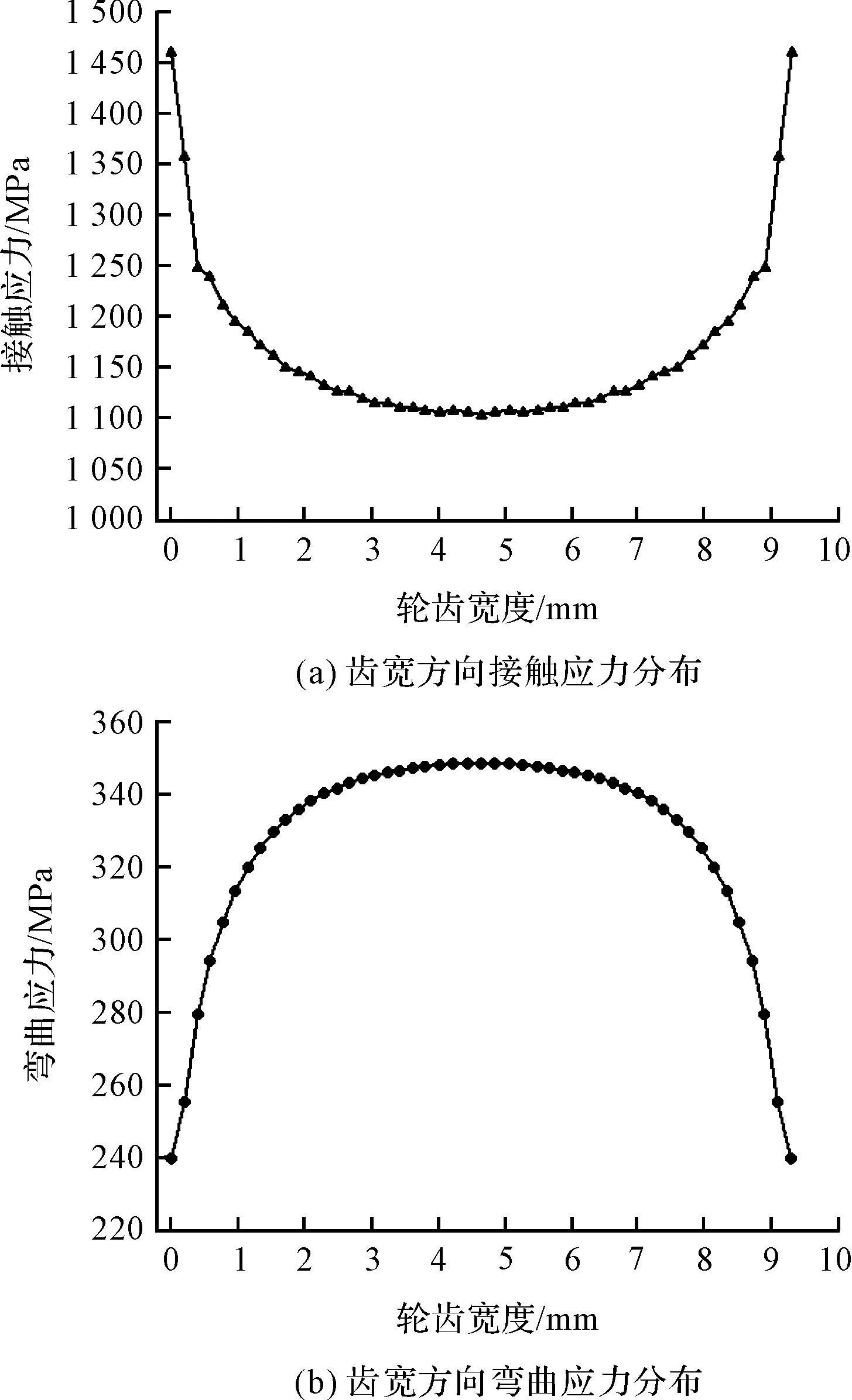
图3 齿宽方向接触应力和弯曲应力分布情况

结合图2(a)和图3(a)可知：大轮上靠近轮齿边缘的地方接触应力较大；通过与其他类型的齿轮分析结果对比发现，这对齿轮正常啮合时轮齿边缘存在较大的应力集中。由图2(b)和图3(b)可知：齿根弯曲应力在齿根中间位置有最大值。

2 鼓形修形对轮齿应力分布的影响

上述齿轮的齿面接触应力在轮齿边缘存在较大的应力集中，在实际应用过程中易出现疲劳点蚀等缺陷[9]。

本文中通过对小轮进行齿向鼓形修形来减小轮齿边缘应力集中的现象[10]。记鼓形修形量为Δ，分别取Δ为20 μm和50 μm建立修形后的小轮模型，通过有限元分析观察鼓形修形对齿面接触应力和齿根弯曲应力的影响情况。

不同修形量对应的齿面接触应力分布情况如图4所示。

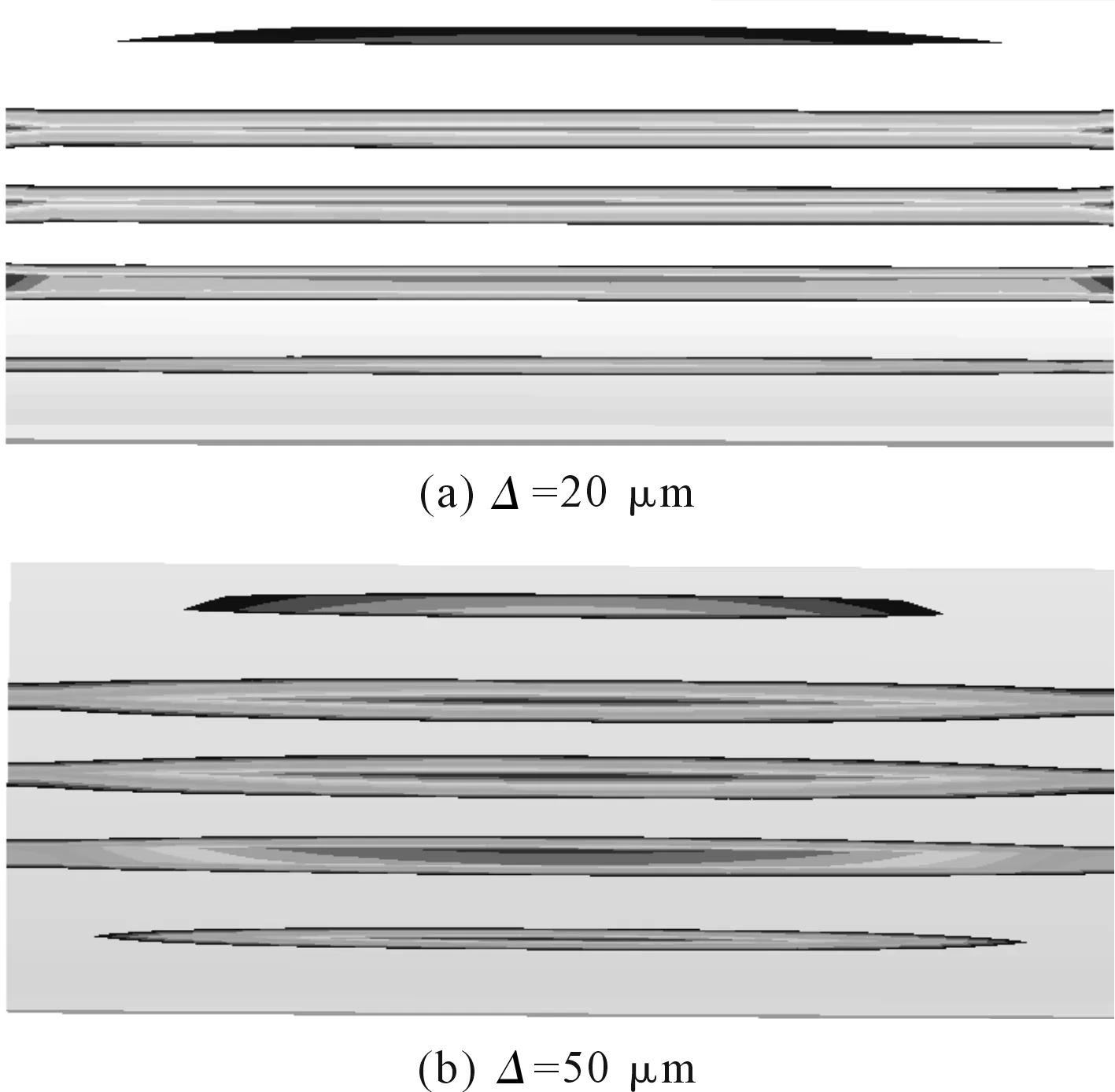
图4 修形后齿面接触应力分布情况

不同修形量对应的齿根弯曲应力分布情况如图5所示。

图5 修形后齿根弯曲应力分布情况

将图(4，5)与图2进行对比可知：修行后轮齿边缘的应力集中得到了改善，齿面接触应力和齿根弯曲应力的最大值仍出现在单齿啮合最高点。该位置接触应力和弯曲应力沿齿宽方向的大小分布如图6所示。

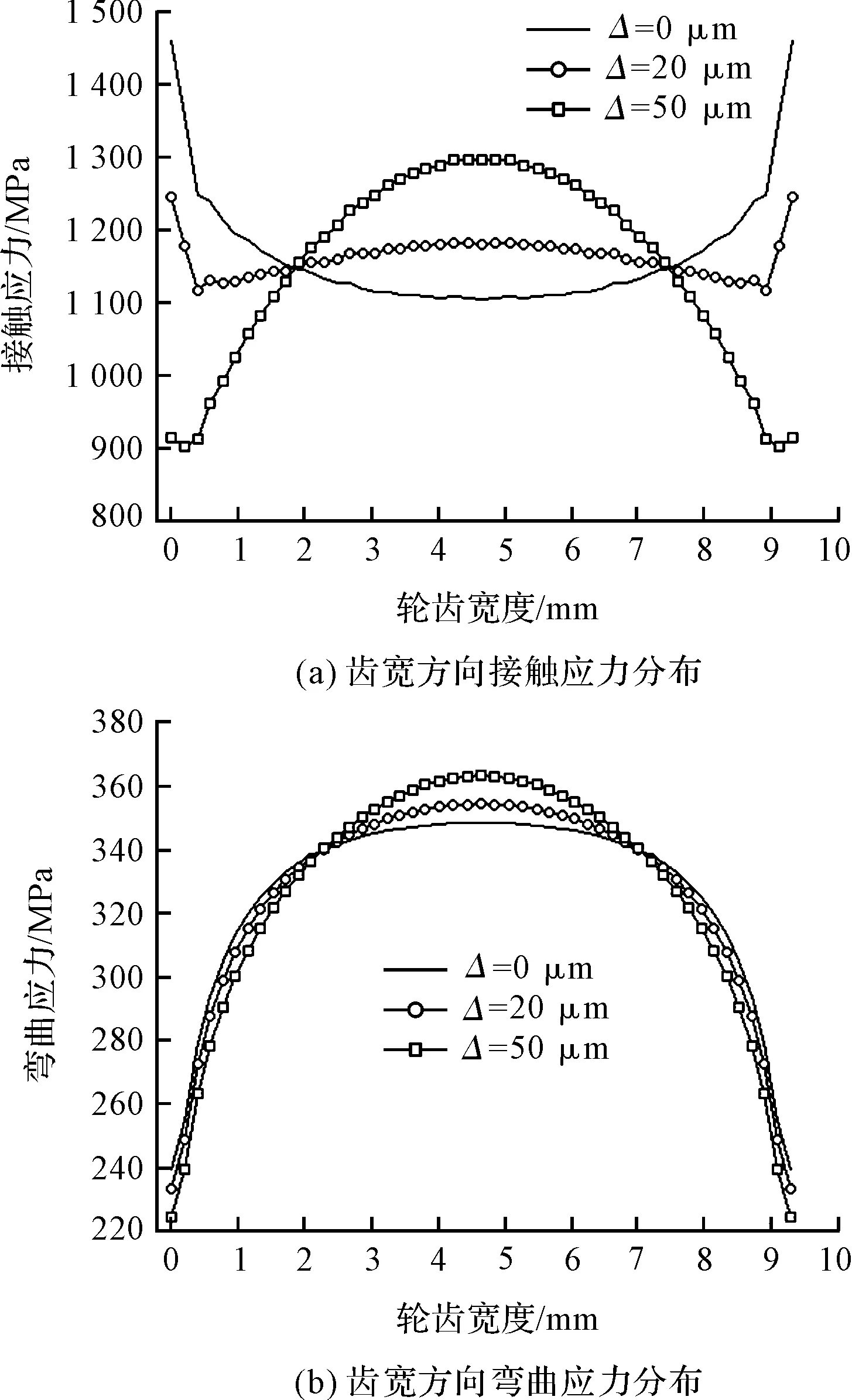
图6 修形前后接触应力和弯曲应力分布情况

由图6(a)可知：修形后齿面接触应力仍存在一定的应力集中。当Δ=20 μm时，轮齿边缘仍有较大的应力集中；当Δ=50 μm时，轮齿中间位置的接触应力最大，边缘处的应力集中对其影响很小，可以忽略不计。因此，上述修形在一定程度上降低了轮齿上的最大接触应力。

由图6可知：修形量越大，轮齿中间位置的接触应力和弯曲应力越大。这是由于修形后接触区域逐渐向轮齿中部靠拢，使得轮齿边缘的应力集中现象得到改善。

修形前后轮齿上的最大接触应力和弯曲应力如表2所示。

表2 修形前后最大接触应力和弯曲应力

由表2可知：齿轮修形后降低了轮齿上的最大接触应力，最大弯曲应力有所增加。当Δ=20 μm时最大接触应力降低了14.7%，最大弯曲应力增加了1.7%；当Δ=50 μm时最大接触应力降低了11.2%，最大弯曲应力增加了4.2%。由于弯曲应力的增幅小于接触应力降低的幅度，当齿轮的齿面接触强度不足而齿根弯曲强度有一定的余量时，可以考虑这种修形方式来提高齿轮的接触强度；对于上述研究对象，最好修形量为20 μm。

3 偏载对轮齿应力分布的影响

过载、瞬间或剧烈的冲击载荷以及严重偏载均易引起突然断齿，造成这种损伤的主要原因是载荷产生的应力超过了材料的强度极限。本文以此为基础通过对小轮施加绕图1中的X2轴和Y2轴旋转的角度误差来研究偏载对直齿轮传动系统应力分布的影响。

记小轮绕X2轴和Y2轴旋转的角度分别为θx和θy，取θx和θy分别为0.1°和0.2°进行研究。

当小轮修形量Δ=0 μm时的接触应力分布情况如图7所示。

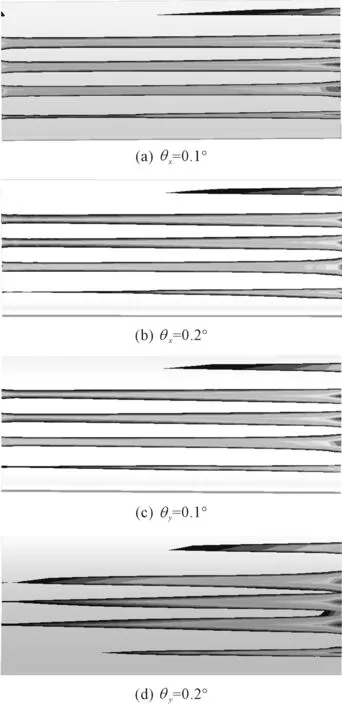
图7 不同偏载量对应的接触应力分布

由图7可知：偏载使齿轮传动系统发生了严重的边缘接触。此时的齿面接触应力和齿根弯曲应力仍在单齿啮合最高点取得最大值，该位置接触应力和弯曲应力沿齿宽方向分布如图8所示。

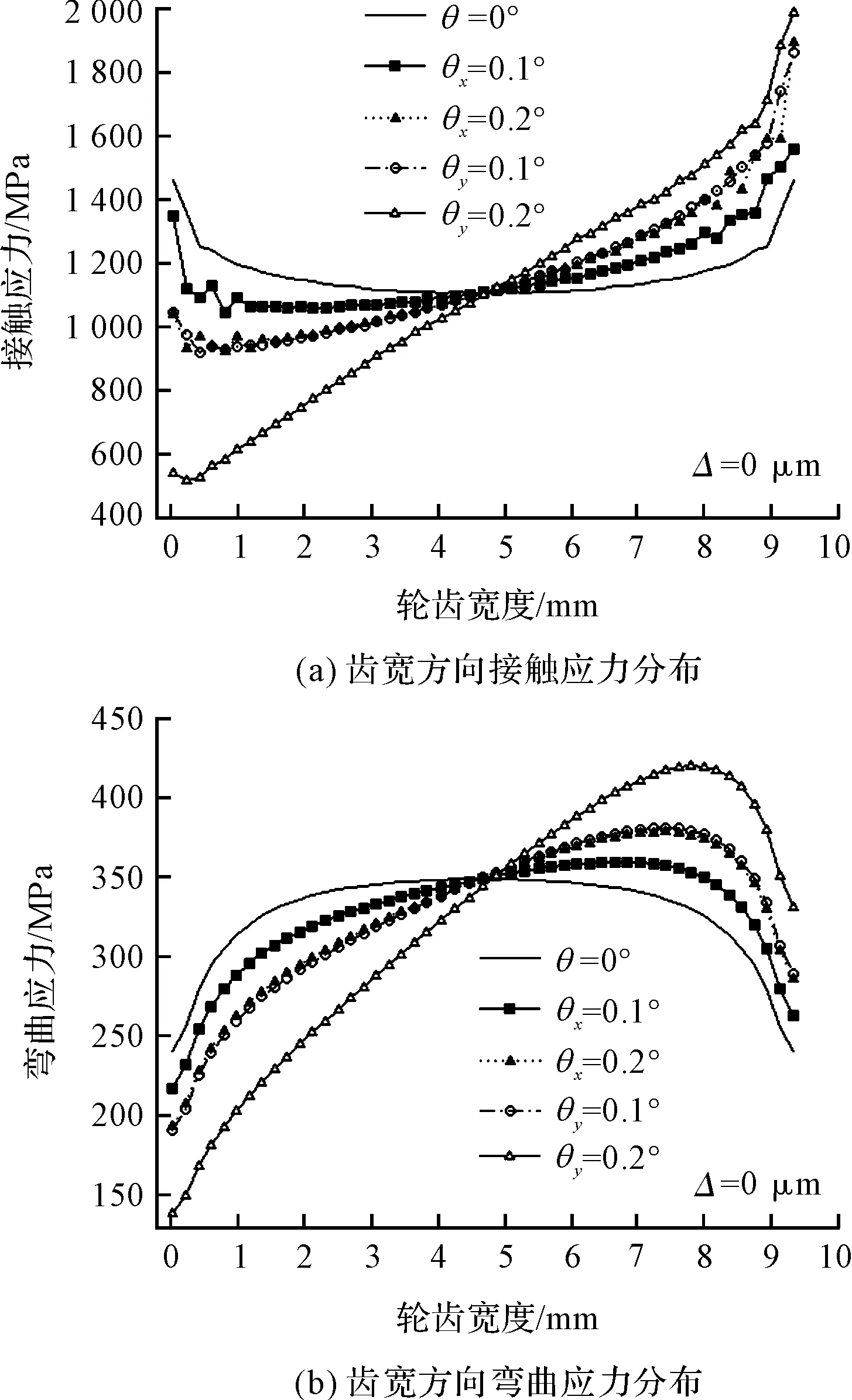
图8 不同偏载量时接触应力和弯曲应力分布

由图8(a)可知：偏载后大轮上发生了边缘接触，且偏载的角度越大，边缘接触越严重，产生的最大接触应力越大。由图8(b)可知：偏载后弯曲应力的作用区域也沿着偏载的方向移动，且偏载角度越大，该区域移动的距离也越大，产生的弯曲应力越大。

以无偏载时最大弯曲应力点的位置为初始点，偏载后最大弯曲应力偏离初始点的距离记为偏移距离，则偏载前后最大接触应力和弯曲应力以及偏移距离的变化情况如表3所示。

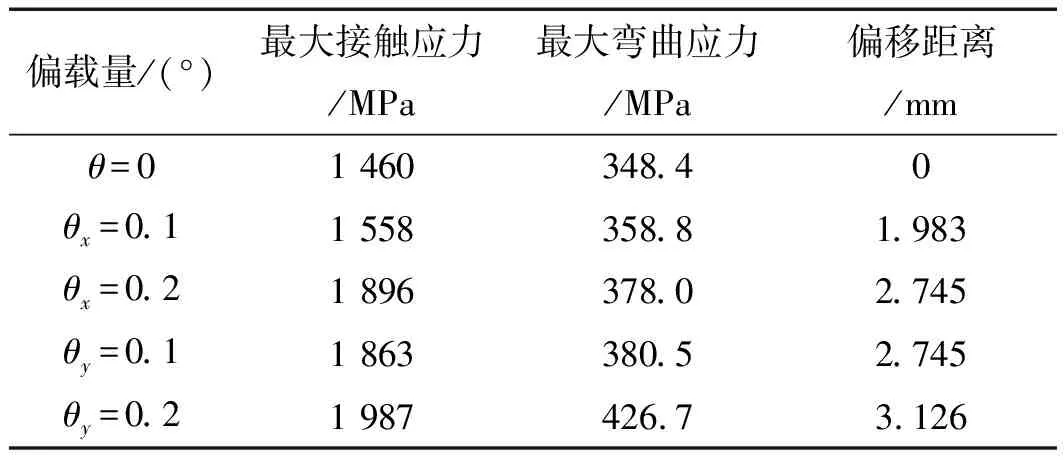
表3 偏载前后最大接触应力和弯曲应力

由表3可知：当角度θx=0.1°时，齿轮接触应力增加了6.7%，弯曲应力增加了3.0%；当角度θx=0.2°时，接触应力增加了29.9%，弯曲应力增加了8.5%；当角度θy=0.1°时，齿轮接触应力增加了27.6%，弯曲应力增加了9.2%；当角度θy=0.2°时，齿轮接触应力增加了36.1%，弯曲应力增加了22.5%。

由此可知：偏载极大地增加了轮齿上的接触应力和弯曲应力。因此，为保证齿轮工作寿命，在齿轮安装和工作过程中应尽量避免偏载。

4 鼓形修形对偏载的影响

由上述分析可知：鼓形修形能适当地降低轮齿边缘的接触应力，偏载会大大增加轮齿上的接触应力。

本研究对修形后的齿轮副引入一定偏载量，研究修形后不同偏载量的齿面接触应力和齿根弯曲应力的大小和分布情况。分析结果如图(9，10)所示。

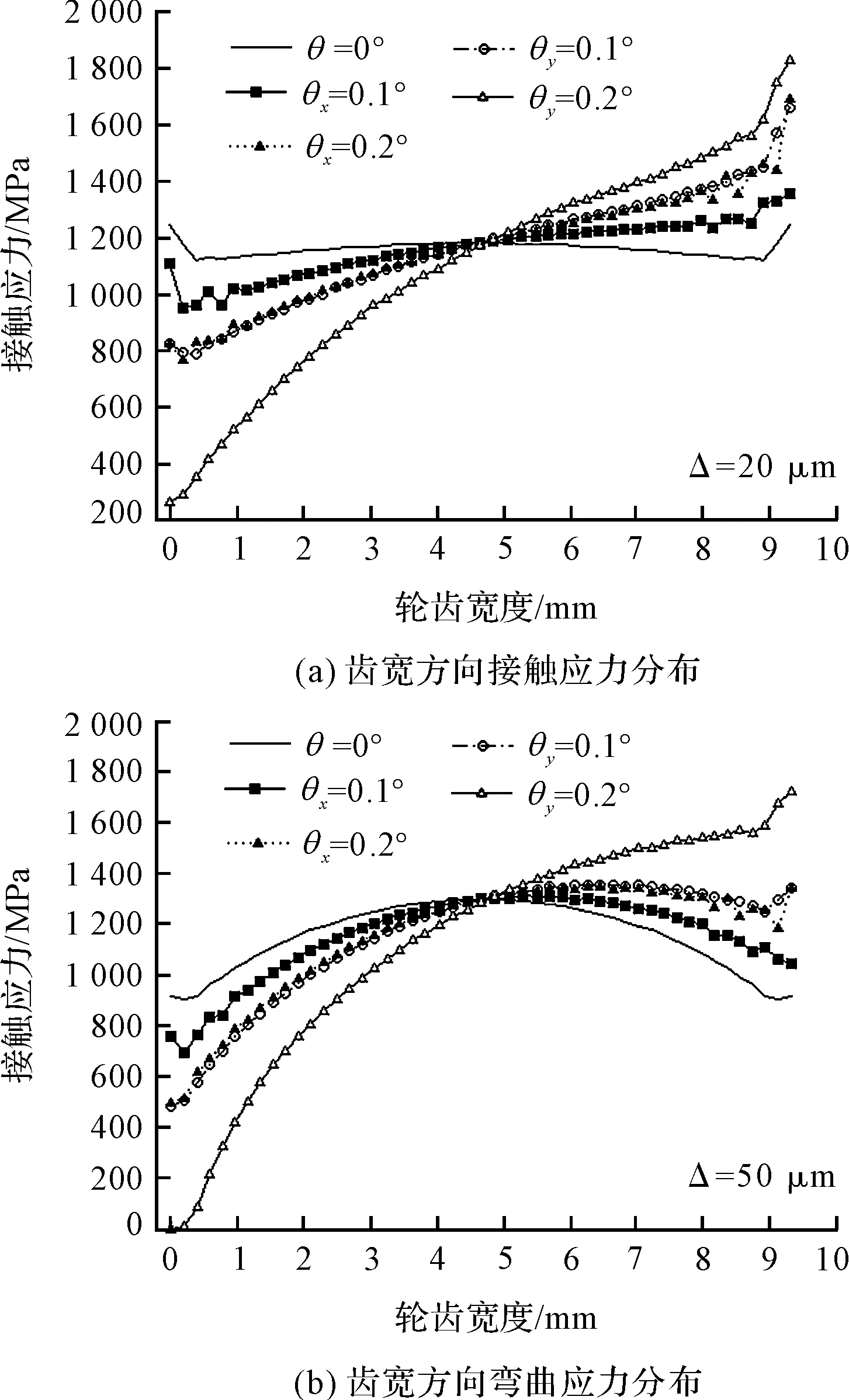
图9 不同修形量和偏载量时接触应力分布

图10 不同修形量和偏载量时弯曲应力分布

由图9和图8(a)可知：适当的鼓形修形能在一定程度上避免因偏载而引起的边缘接触。当Δ=20 μm时仍存在明显边缘接触，当Δ=50 μm时边缘接触的现象得到显著改善。

由图10和图8(b)可知：修形后的齿轮模型发生偏载时，弯曲应力的作用区域也沿着偏载的方向移动。

图(9，10)中最大接触应力、弯曲应力和最大弯曲应力偏移距离的变化情况如表4所示。

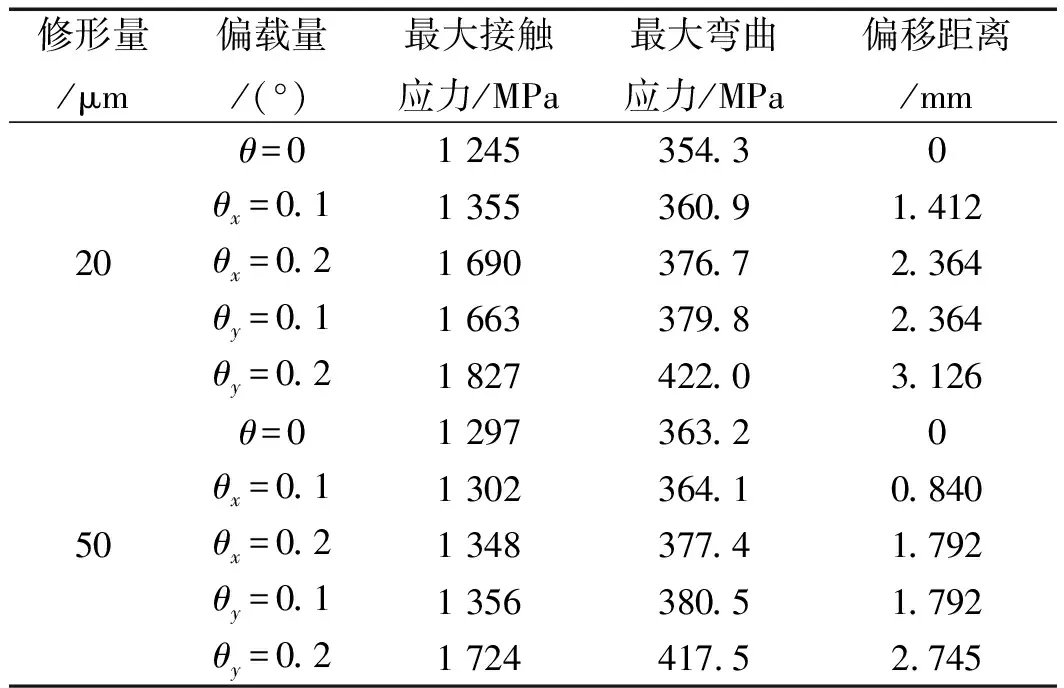
表4 不同修形量和偏载量时最大接触应力和弯曲应力

由表4可知：对于修形后的模型，随着偏载量的增加，最大接触应力、最大弯曲应力和偏移距离都增大。对比表(3，4)可得：在相同的偏载量时，修形后模型的最大接触应力要小于修形前，且修形量越大接触应力越小，抗偏载能力越强；在相同偏载量时，修形前后最大弯曲应力的变化不大，但最大弯曲应力沿着偏载方向偏移的距离存在明显差异，修形量越大，偏移的距离越短。总体而言，当偏载量为θx=0.1°时，修行量Δ取20 μm或50 μm都可以有效改善轮齿边缘的接触应力，对于其余3种情况，修形量Δ取50 μm时偏载效果会更好。