直流侧电压波动对MMC的环流影响机理分析及抑制方法

张夏辉，韩民晓，杨景刚，孟祥坤，邱子鉴

（1.华北电力大学电气与电子工程学院，北京市 102206；2.国网江苏省电力有限公司电力科学研究院，江苏省南京市 210096）

0 引言

随着数据中心、电动汽车充电桩等直流负荷日益增多，中压直流配电网成为未来的发展方向［1-3］。在直流配电系统中，通常采用DC/AC换流器与中压交流配电网相连。其中，以模块化多电平换流器（modular multilevel converter，MMC）最 为 常 见［4］。与传统的两电平、三电平电压源换流器相比，MMC具有开关损耗低、输出电压畸变小等特点，能满足中压直流配电网的实际需求［5-7］。但是由于MMC内部结构复杂，存在谐波环流、子模块电容电压纹波等问题，会影响MMC运行时的状态。

在直流配电网中，直流母线电压波动是一个常见的问题［8］。引起直流母线电压波动的原因大致可分为2类:①与直流配电网连接的中压交流电网出现不平衡故障或谐波，通过换流器传递至直流母线［9］；②光伏、风电等分布式电源和直流负荷等设备通过电力电子装置接入直流配电网，在直流母线上产生由绝缘栅双极型晶体管（IGBT）等元件开关操作生成的调制谐波［10］。由不同原因引起的直流侧电压波动频率不同。文献［11］指出，电网在不平衡工况下，直流侧将产生工频和二倍频波动。文献［9］讨论了当交流侧电网中含有5次、7次谐波分量时，直流侧将存在6次波动。文献［10］表明，换流器的正弦脉宽调制将在直流侧产生载波频率及其整数倍次的谐波，其频率较高，幅值较小，相比于低频谐波容易治理。当直流母线上存在电压波动时，直流母线电压与MMC上、下桥臂的电压和不相等，这是造成MMC内部环流的主要原因［12］。环流的存在将增加MMC的内部损耗，缩短IGBT等开关设备的寿命，威胁MMC的安全运行［13］。

目前，在直流配电网中，直流母线电压波动抑制方案主要可分为无源滤波和有源滤波。其中，无源滤波方案主要是在直流侧并联足够大的电容或选择合适的LC滤波电路［14］。文献［15-16］提出了基于直流有源电力滤波器（DC active power filter，DCAPF）的有源滤波方案。当直流母线电压出现较大幅值波动时，上述2种方案的抑制效果均比较有限，直流母线电压波动在MMC内部会形成较大的环流。

目前最广泛使用的MMC环流抑制控制策略是基于比例-积分（PI）控制器的环流抑制策略，文献［17］将MMC三相桥臂中的二次环流转换至dq坐标系，通过PI控制使其趋近于0。此方法主要针对二次负序环流，当交流电网出现故障或大量谐波时，抑制效果有限。文献［18］提出了一种基于比例-谐振控制器的环流抑制策略，可直接在abc静止坐标系下进行环流抑制，但参考信号和输出信号之间存在相位差，抑制效果有限。文献［19］提出了基于矢量比例积分（VPI）的控制策略，能修正跟踪时的相角偏差，但此方法在直流母线电压波动频率发生变化时，抑制效果不明显。

本文从理论上分析了直流母线电压波动通过MMC传递的规律。从MMC调制的角度出发，建立MMC谐波传递的数学模型，并给出内部环流的数学表达式。针对此环流，本文利用快速全局最小二乘子空间旋转不变（TLS-ESPRIT）方法分析其特性，在此基础上建立了基于PI-VPI控制的自适应环流抑制方法。利用子模块的储能能力，改变MMC调制函数以减小环流，降低因环流而导致的开关管过 热，保 证 系 统 安 全［20］。最 后，在MATLAB/Simulink平台上搭建了仿真模型，对上述结论进行了验证。

1 MMC拓扑结构

MMC的基本结构如附录A图A1所示，主体部分由三相桥臂构成，每一相桥臂由上、下桥臂构成，每一个桥臂中均含有2N个子模块。

在实际运行过程中，x相上桥臂导通的子模块个数为Npx，下桥臂导通的子模块个数为Nnx，其中x=a、b、c，则存在如下关系［3］。

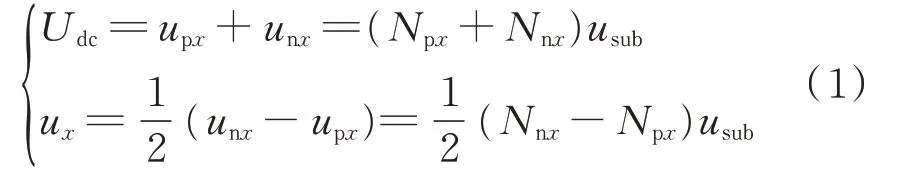
式中:Udc为直流母线电压；upx和unx分别为x相上桥臂电压和下桥臂电压；ux为x相交流输出电压；usub为子模块电压平均值。

由式（1）可得出如下结论。

1）同一时刻、同一相的上桥臂导通的子模块个数与下桥臂导通的子模块个数相加等于N，用以维持直流侧电压稳定。

2）改变上、下桥臂导通子模块数量之差可改变输出电压幅值。

2 直流母线电压波动工况下的MMC环流计算

在MMC正常运行状态下，假定MMC三相参数相同，交流侧接入三相对称交流源。同时，MMC中的二次负序环流部分假定已抑制完成。抑制环流的主要方法是在原有的调制函数中叠加一个二倍频分量［13］，其幅值远小于调制基波分量，可忽略该分量。当直流母线上存在电压波动时，假定波动的频率为ωh，此波动可等效视为在直流母线上叠加了一个频率为ωh的交流电源，造成三相桥臂和直流母线之间产生电压差。此电压会降落在桥臂的电阻与电感上，必然会产生频率为ωh的零序环流。此时，MMC内部三相上、下桥臂的电流可表示为:

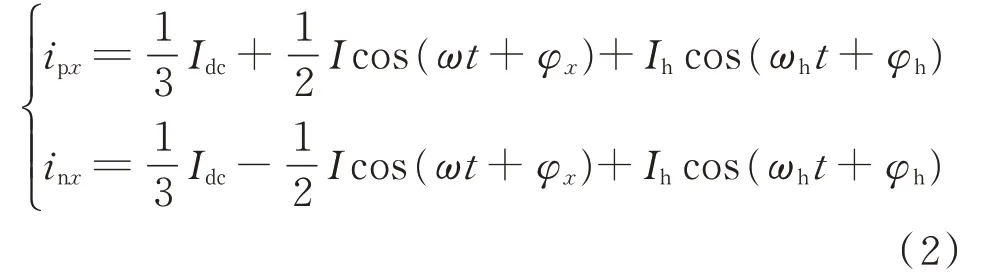
式中:ipx和inx分别为上、下桥臂电流；Idc为直流侧电流幅值；I为单相交流侧电流幅值；ω为工频频率；φx为x相电流的初始相角；Ih为频率为ωh的电流成分的幅值；φh为该电流成分的初始相角。

在MMC中，可以使用平均值模型来描述桥臂上子模块的开断情况［11］，以a相为例进行说明。假定a相的输出相角为0°，b、c相依次滞后120°。通过上述修正的上、下桥臂的电流和开关函数，可以计算上、下桥臂的子模块电容电压中频率为ωh的电压波动为:

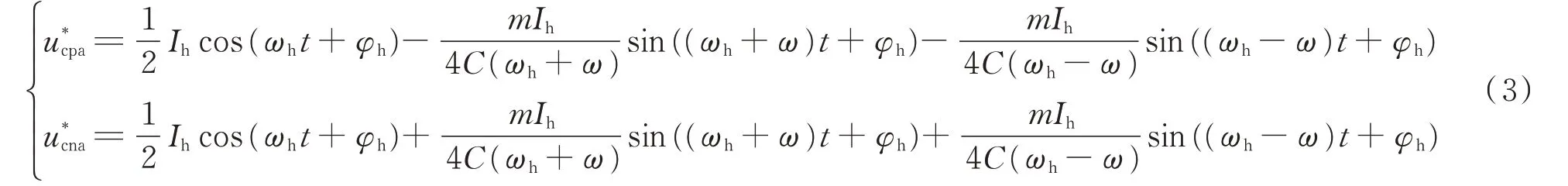
根据式（3）得出子模块电压值，可以进一步推导出上、下桥臂电压和a相桥臂总电压中和ωh有关的部分，即

由式（3）可以看出，因频率为ωh的直流电压波动产生的频率为ωh的环流，将在子模块电容电压中产生频率为ωh和ωh±ω的电压波动，且上、下桥臂电容波动相位恰好相差180°。同样，由式（4）和式（5）可以看出，在上、下桥臂的电压波动中，频率为ωh±ω的电压波动相位恰好相差180°，在计算相电压时相互抵消，剩下ωh−2ω、ωh、ωh+2ω这3个频率的电压波动，且上、下桥臂相应频率的电压波动相位相同，呈正序性质。

根据式（6）可推出，由频率为ωh的直流波动产生的频率为ωh的三相零序环流，将在桥臂电容上产生频率为ωh±ω的电压波动，并在桥臂电压上产生频率为ωh-2ω、ωh+2ω的正序波动，进而产生频率为ωh−2、ωh+2的环流。由此规律进行外推，频率为ωh−2ω、ωh+2ω的环流又会使得子模块电容电压上产生频率为ωh−3ω、ωh−ω、ωh+ω、ωh+3ω的波动，在桥臂总电压上产生频率为ωh−4ω、ωh+4ω的 电 压 波 动，进 而 导 致 产 生 频 率 为ωh−4ω、ωh+4ω的环流。由此分析可知，当直流侧存在频率为ωh的电压波动时，在桥臂内部存在频率为ωh±2kω（k=0，1，…）的环流。

根据以上分析，进一步将上、下桥臂的电流修正为:

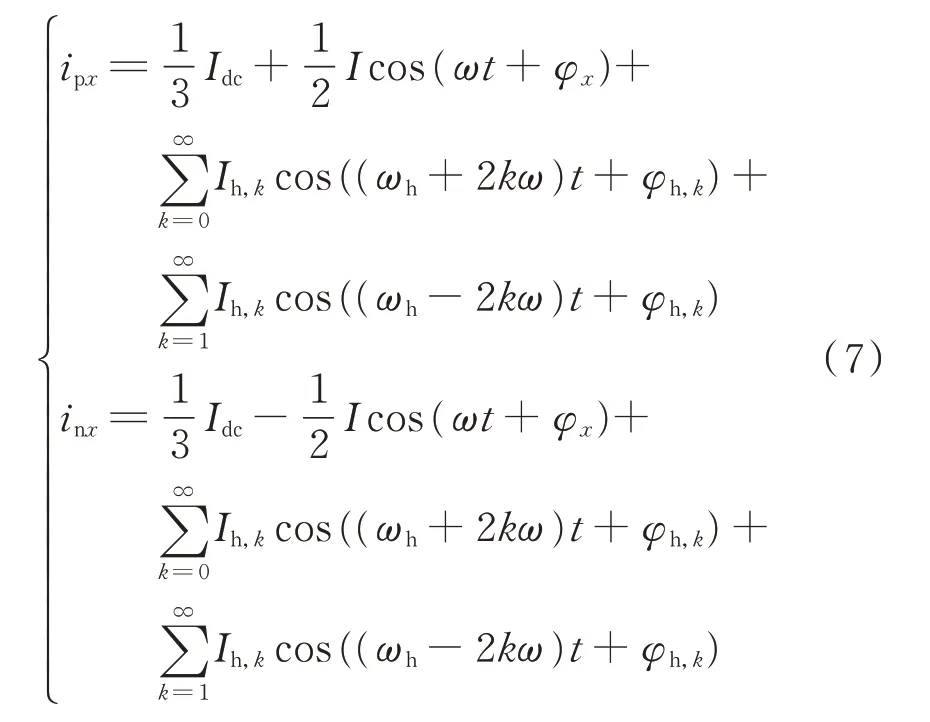
式中:Ih，k为频率为ωh−2kω的环流幅值，其中k≥0且k为整数；φh，k为其初始相位。

以a相为例，将式（7）代入式（4）至式（6），取出其中频率为ωh的波动部分如下。

式 中:φh，0和Ih，0分 别 为 频 率 为ωh的 环 流 相 角 和 幅值；φh，1和Ih，1分别 为 频率为ωh−2ω的环流 相角和幅值。由上文分析可知，频率为ωh−2kω的环流都是由频率为ωh−2(k−1)ω的电压波动产生的，且随着k的增大，幅值呈逐渐递减的趋势，故在数值上存在Ih，0≫Ih，1。忽略式（8）中的Ih，1，将其修正为:

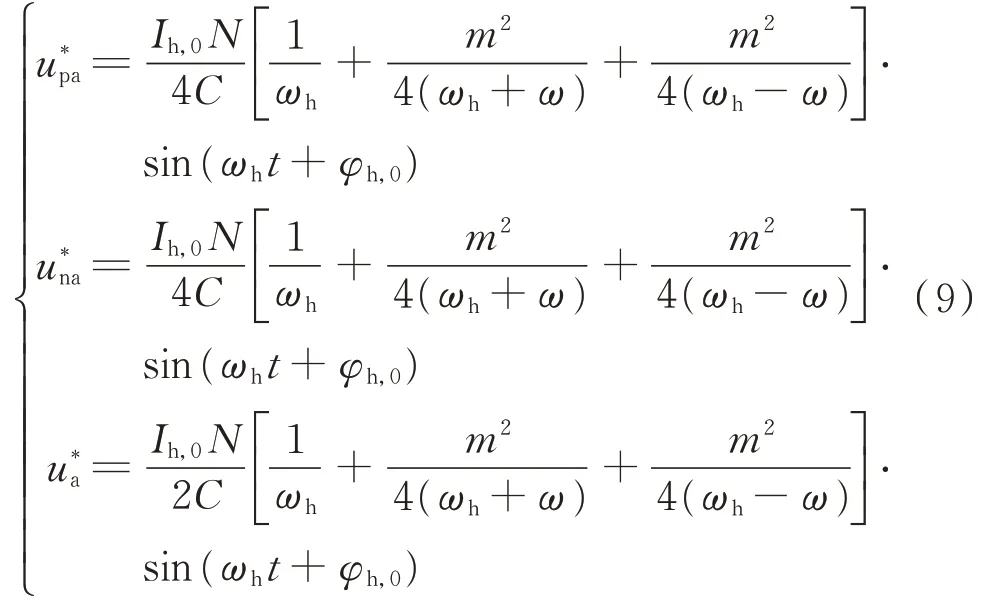
此时，根据叠加定理，针对整个MMC系统中频率为ωh的成分，可以做出一个等效电路图，如附录A图A2所示。图中，uha、uhb、uhc分别为a、b、c相桥臂频率为ωh的电压波动成分；uhs为母线电压波动值；iha，0、ihb，0、ihc，0分别为a、b、c相频率为ωh的环流成分；ihs为母线电流波动成分。

根据式，将uhx写成相量形式:

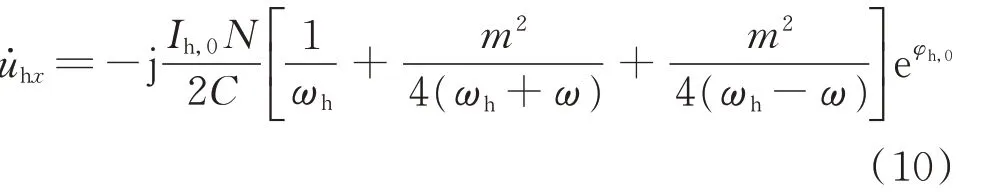
根据基尔霍夫电压定律（KVL），对附录A图A2任意一相列写电压平衡方程。

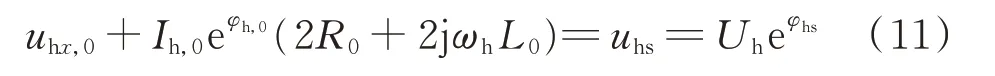
式中:Uh为电压波动幅值；R0和L0分别为桥臂电阻和桥臂电感；uhx，0为桥臂电压波动控制值；φhs为母线环流相角波动值。

联立式（10）和式（11），可解出频率为ωh的环流幅值为:

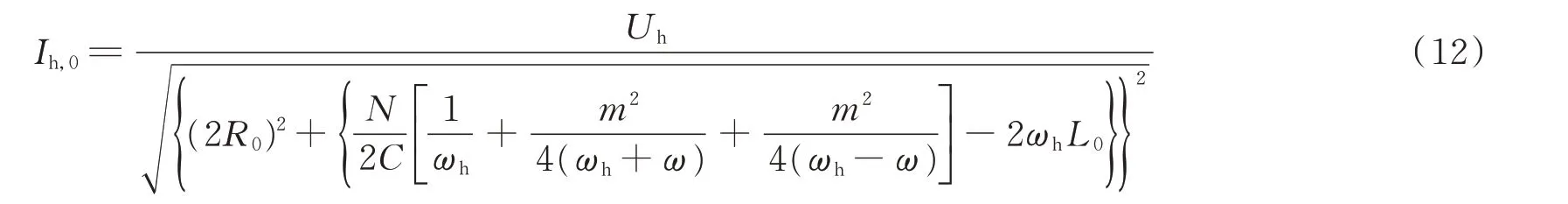
3 谐波环流抑制策略

根据第2章计算，当MMC直流母线出现电压波动时，MMC内部桥臂将激励出显著的同频环流，且主要呈零序的形式。因此，本文提出一种控制策略，通过辨识直流母线上的电压波动频率，设计自适应控制器改变MMC调制函数以抑制波动，其目标是控制三相桥臂中的特定频率零序谐波为0。

3.1 快速TLS-ESPRIT方法

配电网中接入了很多非线性负荷和电源，谐波问题较为严重，例如传统的整流装置将产生5次、7次谐波。此外，交流配电网中还存在大量的间谐波［21］。这些谐波经过换流器传导到直流侧，形成对应频率电压波动，传统的快速傅里叶变换（FFT）方法无法精确检测谐波频率。在现有的谐波频率检测方法中，快速TLS-ESPRIT方法具有计算速度快、抗噪能力强、辨识度高且频率估计较为精准等特点，适合快速判断直流母线的电压波动频率。

3.2 环流抑制策略

根据附录A图A2的等效电路，当环流流经桥臂电感、电阻时将产生压降，其对应的KVL方程为:

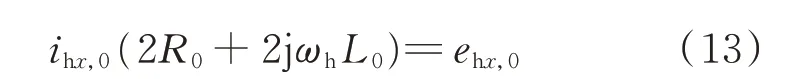
式 中:ihx，0为 任 意 一 相 的 环 流；ehx，0为 任 意 一 相 由 环流产生的桥臂阻抗电压波动。

根据式（13）可以设计附加控制器跟踪此电压，使其变成桥臂电压修正量的参考值，进而通过调制使得每一相的共模电压值跟踪母线电压的变化，最终实现环流的抑制。由于需要跟踪的量为交流量，为保证无差跟踪，本文选择PI-VPI控制器作为附加控制器，其闭环控制框图如图1所示。

图1 基于PI-VPI控制器的环流抑制框图Fig.1 Block diagram of circulating current suppression based on PI-VPI controller

图1中:ih，0，ref为 环 流 的参考值；GPI-VPI为PI-VPI控制器的传递函数；GS为系统传递函数。

式 中:GPI为PI控 制 器 的 传 递 函 数；GVPI为VPI控 制器的传递函数；kip为PI控制器的比例系数；kii为PI控制器积分系数；kp为VPI控制器的比例系数；kr为谐振系数；ωc为谐振带宽且取ωc=10 rad/s。

根据文献［19］所述，通过调整kp和kr的相对大小，可改变PI-VPI控制器在谐振点的相位响应。为了使图1中的ihx，0保持对ih，0，ref的无差跟踪，kp和kr应满足以下条件。

取kp=0.1，R0=1Ω，L0=10 mH，由式（16）计算可得kr=100。参照文献［22］，PI控制器部分参数可设置为kip=0.001 3，kii=0.13。直流母线处谐波以偶数次谐波为主，所以取特征谐振频率ωh为100、200、400 Hz，分别作控制器传递函数、系统开环传递函数和系统闭环传递函数波特图，如图2所示。

图2（a）中，当谐振频率ωh不同时，控制器在谐振点的相频特性相同，均为61.7°。图2（b）中，不同谐振频率的系统开环传递函数在谐振点的幅频特性相同，均为14 dB。图2（c）中，不同谐振频率的系统闭环传递函数在谐振点的相频特性相同，均为0°，且幅频特性均为0 dB。从上述分析可知，在频率较低范围内，改变PI-VPI控制器的谐振频率，保持其余参数不变，系统和控制器在谐振点的传递函数特性均不变，且闭环系统均能保持对输入信号的无差跟踪。

由第2章分析可知，三相桥臂共模电流中与直流母线电压波动频率相同的成分呈零序形式。为抑制此部分电流，设计对应谐振频率的PI-VPI控制器，并与原有的二倍频环流抑制控制相结合，可以得到包含自适应PI-VPI控制器的MMC环流抑制系统，如图3所示。

图3中，iza、izb、izc分 别 为 三 相 桥 臂 的 共 模 电 流；Ucoma、Ucomb、Ucomc分 别 为 三 相 输 出 修 正 电 压；θ为 锁相环输出的交流侧a相相角。三相桥臂的共模电流经过派克变换后，dq轴的输出量仍经过原先的2次环流抑制过程。0轴输出量经过TLS-ESPRIT分析，分离信号中的各个频率成分，利用其中的各个波动频率分别生成对应VPI控制器。将原始信号经PI控制器与所有VPI控制器后相加，生成三相输出修正电压的0轴分量，与原2次环流抑制后的dq轴结果一起进行派克逆变换，生成三相输出修正电压。

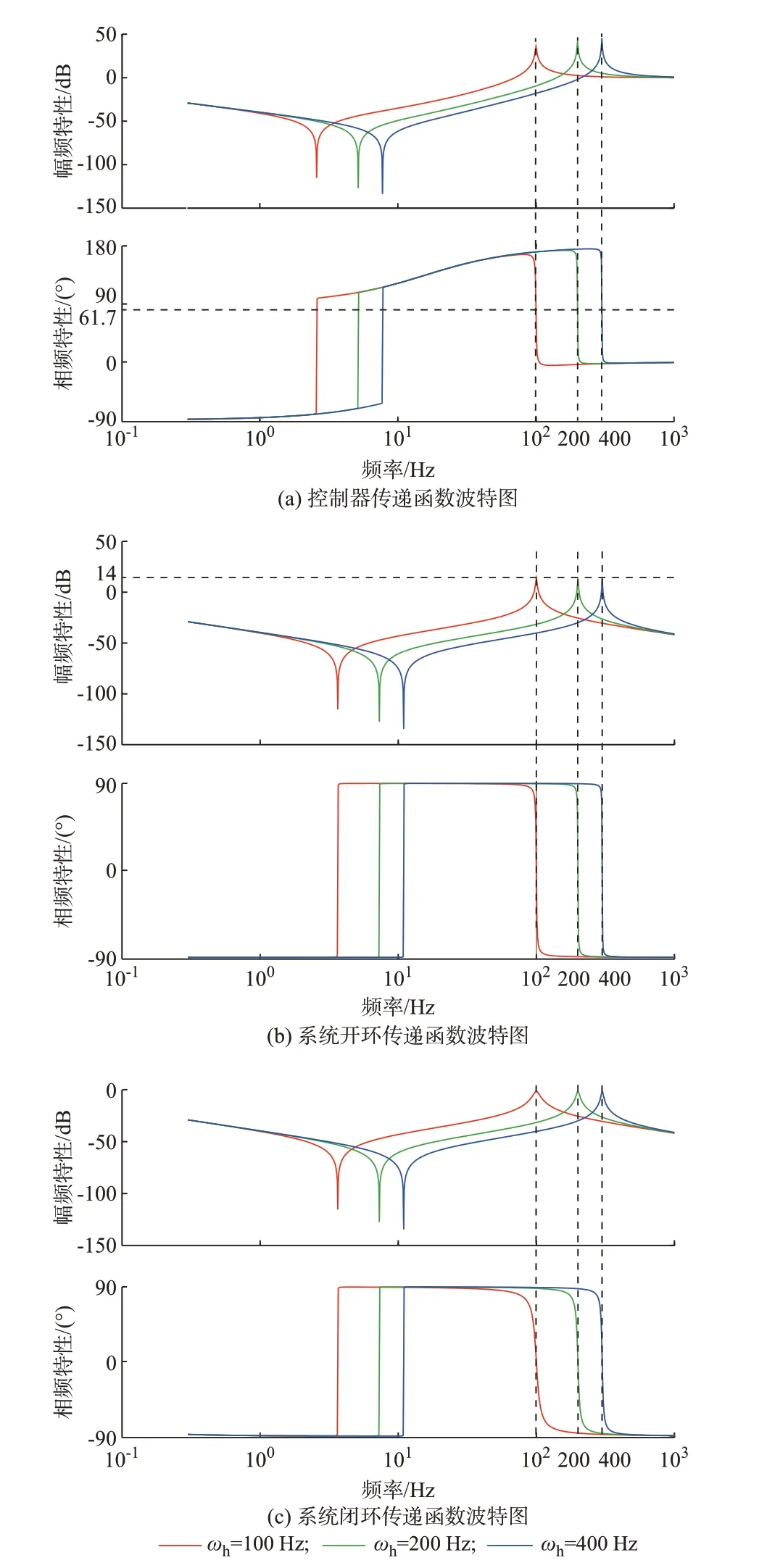
图2 不同谐振频率下PI-VPI控制器、开环系统和闭环系统传递函数波特图Fig.2 Bode diagrams of PI-VPI controller,open loop system and closed loop system with different resonance frequencies

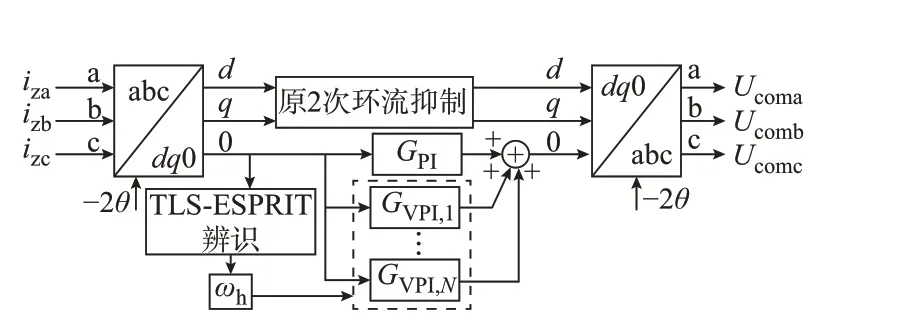
图3 环流抑制策略Fig.3 Strategy of circulating current suppression

4 仿真分析

为了验证上述分析的正确性，结合附录A图A3所示的中国苏州同里中压直流配电示范工程进行仿真研究。因MMC1侧的交流系统AC1中存在不平衡功率、谐波注入，或MMC1自身参数三相不对称造成自身交流电压不平衡等情况，直流母线电压发生周期性波动，对MMC2及其交流系统产生影响。取图A3中虚线框部分，在MATLAB/Simulink平台上搭建单端换流器系统，如附录A图A4所示。变压器采用星形/三角形接法，MMC的具体参数如附录B表B1所示。

4.1 存在波动时环流大小验证

首先，验证波动频率与桥臂环流的关系。假定直流母线电压波动幅值均为2 kV，在不同频率下的环流幅值计算值与仿真值如图4（a）所示。从图4（a）可以看出，随着频率增大，环流大小逐渐下降，但下降幅度逐渐趋缓。

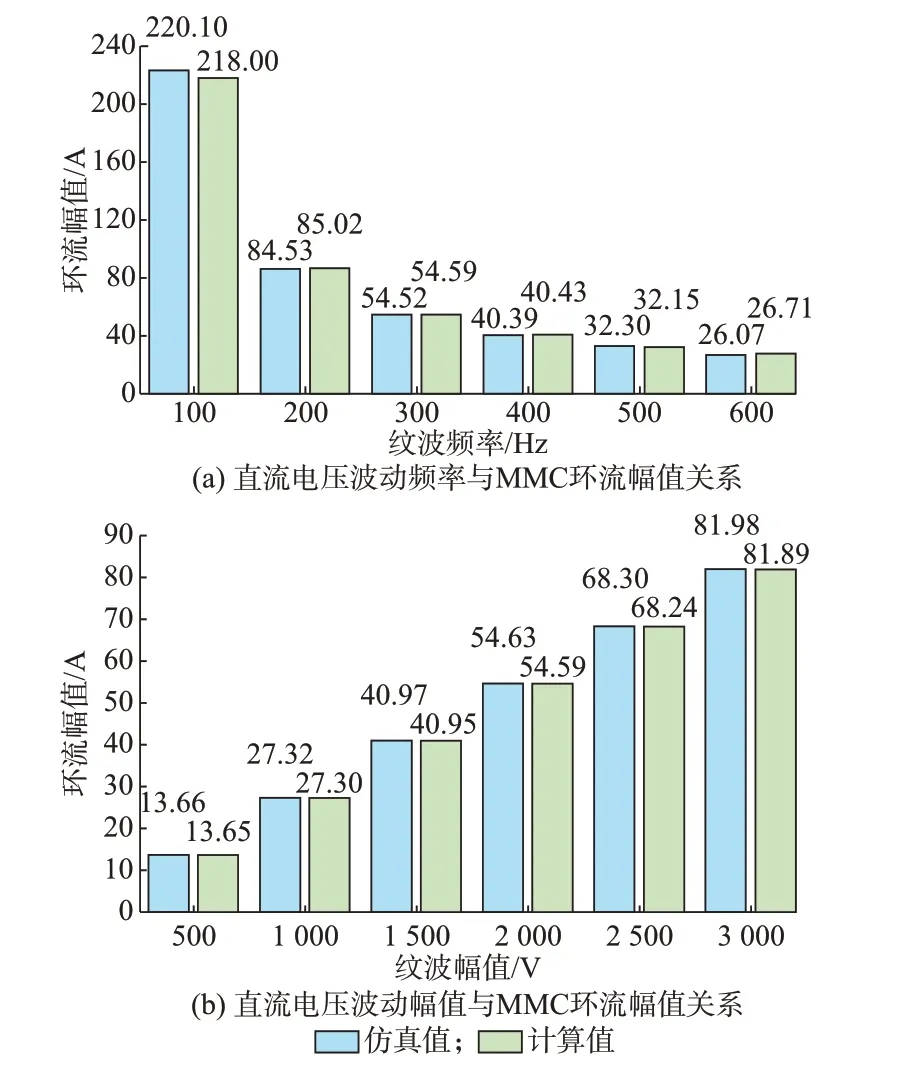
图4 直流电压波动与环流幅值关系Fig.4 Relationship between DC voltage fluctuation and circulating current amplitude

其次，验证波动幅值与桥臂环流的关系。假定直流母线波动频率固定为300 Hz，在不同波动电压幅值的条件下桥臂环流幅值计算值与仿真值如图4（b）所示。从图4（b）可以看出，桥臂环流幅值随直流母线电压波动幅值的增大而增大，两者基本呈线性关系。

在上述2种情况中，计算值与理论值误差很小，基本吻合，充分验证了式（12）的正确性。

4.2 环流频率辨识验证

为了探究一般情况下该环流抑制控制的有效性，保持其他原有控制器和设备的参数不变。假定直流母线电压波动频率为fr，根据第2章分析并考虑测量误差，可将MMC任意一相的桥臂环流表示为:

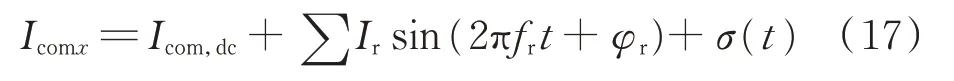
式中:Icom，dc为共模电流中的直流成分；Ir为频率为fr的环流幅值；φr为频率为fr的环流相角；σ(t)为高斯白噪声。现设定在直流母线上分别有频率为240 Hz、300 Hz，幅值为2 kV的电压波动，模拟第3章控制策略中0轴含有白噪声的输出信号，如附录A图A5、图A6所示，其中数据采样频率均为10 kHz，采样时间为0.01 s。

将附录A图A5至图A7中的3组信号分别通过FFT方法与3.1节所述方法进行频率辨识，结果如附录A图A8至图A10和表1所示。

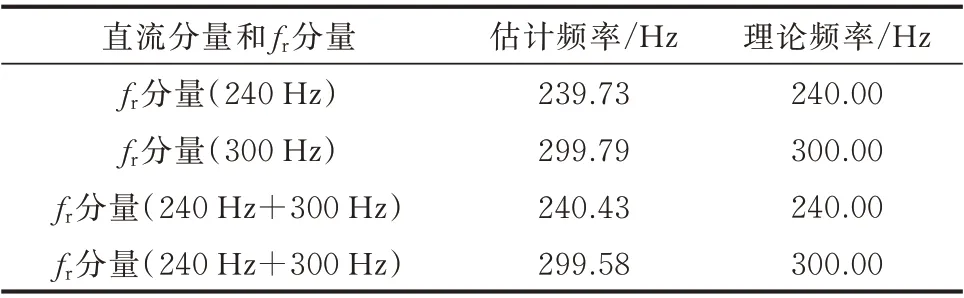
表1 采用TLS-ESPRIT方法的信号辨识结果Table 1 Signal identification results using TLS-ESPRIT method

从附录A图A8和图A10可以看出，由于采集信号长度较短，FFT方法频率分辨精度较差，仅有100 Hz，且存在严重的频谱泄露问题，无法精确辨识信号中的波动频率。从图A9可以看出，若波动频率仅含有100 Hz的整数倍，则FFT方法可准确识别。

表1为采用TLS-ESPRIT方法时的辨识结果。其中，当信号中仅含有单一频率的波动时，fr分量的频率识别差距分别为0.27 Hz、0.21 Hz。当信号中含有2种频率波动叠加时，fr分量的频率识别差距分别为0.43 Hz、0.58 Hz，略大于单一频率。控制器设计时理论带宽为1.59 Hz，均可满足。因此，频率计算误差对控制器输出影响较小，可通过取整消除。综上所述，信号辨识结果基本符合理论值，其结果可以用于后续控制系统的参数设计。

4.3 环流抑制策略验证

根据附录A图A4所示仿真电路，分别设定电压波动频率为240 Hz、300 Hz、240 Hz与300 Hz叠加3种电压波动情况进行仿真。其中，各频率电压波动幅值均为2 kV。在0～0.5 s投入MMC的dq解耦控制和2次环流抑制控制。在0.5 s投入本文所提出的控制策略以消除直流母线波动对MMC造成的影响。通过4.2节所述的信号辨识，控制策略获取对应谐振频率参数。经取整后，对于电压波动频率为240 Hz和300 Hz的情况，分别设定VPI控制器的谐振频率为240 Hz和300 Hz。同样，对于240 Hz与300 Hz叠加的情况，并联VPI控制器使用参数为240 Hz和300 Hz。投入控制前后MMC直流母线、a相环电流及子模块电压分别如图5所示。由图5可以看出，在策略投入之前，直流母线和MMC桥臂内有明显的谐波环流，谐波频率与直流母线电压波动频率相同，原有的2次环流抑制策略并不能起到很好的抑制谐波环流的作用。子模块电压中也存在电压谐波，主要波动频率为ωh、ωh±ω。其中，频率为ωh的波动成分占主导地位。因此，在下文中主要分析频率为ωh成分的幅值，如表2至表4所示。当直流母线电压波动频率为240 Hz时，MMC单相环流均在69.3 A左右，子模块电压波动幅值为3.237 V。当波动频率为300 Hz时，环流大约为54.5 A，子模块电压波动幅值为2.046 V，均略小于240 Hz时的幅值。当直流母线波动为240 Hz与300 Hz的电压波动叠加时，环流中240 Hz成分幅值为69.3 A，300 Hz成分幅值为54.6 A。子模块电压波动中240 Hz成分幅值为3.278 V，300 Hz成分幅值为2.041 V，基本与对应频率单独作用时的幅值相同。这说明若直流母线波动存在多频率同时作用的情况，当频率之差不为工频整数倍时，不同频率波动对环流与子模块电压波动的影响相互独立。此外，直流母线的电流谐波大致等于三相环流之和，说明此环流基本不流入MMC的交流侧。

表2 环流抑制前后波动分量幅值对比(fr=240 Hz)Table 2 Comparison of fluctuant component amplitudes before and after circulating current suppression(fr=240 Hz)

表3 环流抑制前后波动分量对比(fr=300 Hz)Table 3 Comparison of fluctuant component amplitudes before and after circulating current suppression(fr=300 Hz)

表4 环流抑制前后含2种频率波动分量的对比Table 4 Comparison of fluctuant component amplitudes with two frequencies before and after circulating current suppression

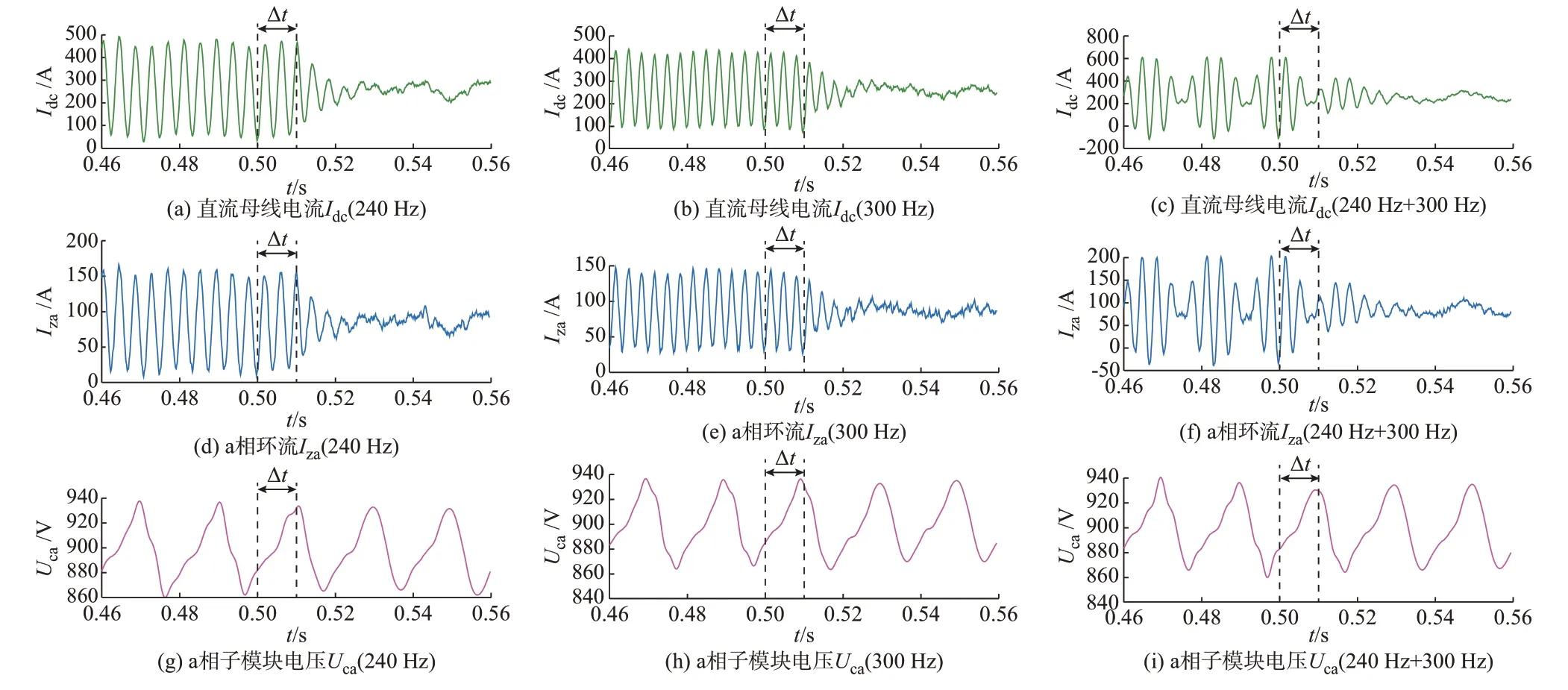
图5 MMC直流母线电流、a相环流和子模块电压Fig.5 DC bus current of MMC,circulating current and sub-module voltage of phase a

由图5可以看出，在0.5 s投入本文所提策略后，控制器首先经过Δt=0.01 s的频率辨识时间。成功获取波动频率后，MMC生成对应VPI控制器进行环流抑制。直流母线、三相环流中的谐波环流和子模块电压波动均在0.035 s内得到明显的抑制。根据表2至表4中的环流抑制策略投入前后谐波环流幅值大小可知，在直流母线电压波动频率为240 Hz时，环流抑制比（抑制后幅值/抑制前幅值）为3.2%，子模块电压波动抑制比为15.9%。当波动频率为300 Hz时，环流抑制比为3.8%，子模块电压波动抑制比为21.1%，效果均较为显著。当直流母线波动为240 Hz与300 Hz的电压波动叠加时，环流中240 Hz成分抑制比为3.5%，300 Hz成分抑制比为4.5%，子模块电压波动中240 Hz成分抑制比为15.3%，300 Hz成分抑制比为19.9%。抑制效果基本与对应频率单独作用时相同，证明本文所提控制策略同样适用于直流母线电压波动多频率相互叠加的情况。在抑制过程结束达到稳定状态后，直流母线各频率电流波动幅值均约为8 A。

在直流配电系统中，参照交流系统中对谐波的定义，240 Hz为间谐波，300 Hz为6次谐波。根据上述仿真结果可知，本文所提控制策略对整数次谐波和间谐波均有良好的抑制效果，具有广泛的适应性。

5 结语

本文分析了直流母线电压波动对MMC内部环流的影响，得出了MMC直流母线电压波动至MMC内部环流的传递关系。当直流侧存在电压波动时，桥臂内部将存在频率为ωh±2kω的环流且频率为ωh的环流最为显著。环流幅值与波动电压的幅值、频率有关，其中环流幅值与波动电压幅值呈正比关系，与波动电压频率近似呈反比关系。

根据上述结论，设计了基于PI-VPI控制器的自适应控制策略来消除此环流的影响。该控制策略方法简单，响应速度较快，抑制效果好，具有一定的通用性，能有效抑制由直流母线波动引起的MMC内部环流，有效保护MMC设备的安全运行，且无须预先预测波动频率，可单独在受直流母线波动影响的MMC上使用。当不同种类设备接入电网时，在直流母线上产生频率不同的电压波动，本文所提控制策略也可自动识别波动频率，生成对应控制器以抑制环流，起到良好的抑制效果，保护换流器设备。

本文所述控制策略对直流母线电压有一定的跟随性质，对直流母线电压波动情况影响较小，在后续工作中将继续研究如何抑制直流母线电压波动。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。