改进时域反演算法在配电网故障定位中的应用

张明一，孙元章，黎 雄，徐 箭，廖思阳，陆裕富

（武汉大学电气与自动化学院，湖北省武汉市 430072）

0 引言

配电网的安全稳定运行与人民的生活质量息息相关，相较于点对点传输输电线路成熟的故障定位技术［1-4］，配电网更加复杂的拓扑使其故障定位变得困难。随着分布式电源（distributed generator，DG）的接入，改变了配电网单一的集中式供电结构，因而配电网的各种保护与控制设备无法做到准确整定，供电可靠性受到挑战，故快速、准确地判断故障位置并排除故障从而尽快恢复供电具有重大意义。

目前，学者针对配电网故障定位问题的研究重点集中在行波法，原理上可分为单端法［5］和多端法［6］，在面对电缆线路和架空线路混合的线路时还存在2种线路波速的换算问题［7］。配电网复杂的拓扑结构使得行波波头来源难以辨识，因此，需要利用合适的故障区间寻找算法［8-10］将所研究配电网从复杂拓扑转化为简单拓扑，再使用行波法在故障区间内实现精确定位。可以预见的是当拓扑更复杂时，为达到较好的精度和鲁棒性，势必会增加行波检测装置数量和故障区间算法的复杂性。将仅获取故障引起的行波波头到达时间扩展到对整个行波信号进行分析，故障引起的行波信号能提供更多的信息。

文献［11］通过频域分析将时域反演（time reversal，TR）概念第1次应用到电网，文献［12］将该理论从频域推广到时域，时域反演理论在串补输电线路故障定位［13］、多端高压直流电网故障定位［14］、高压直流输电系统电压源换流器故障定位［15］、径向网状交直流网络故障定位［16］等领域得到验证。时域反演理论尝试在实际电网进行试验［17-18］，并取得不错的定位效果。以上文献使用电磁时域反演时的一个重要假设是在所研究的暂态过程中，系统的拓扑结构保持不变，在反演阶段建立的仿真模型保持与故障时线路一致，包括线路拓扑、分布式参数、故障类型、过渡电阻等，要求故障发生时不仅需要记录故障引起的暂态信号，还要获取故障类型、过渡电阻等信息。而在实际配电网中，不同时间发生的故障相关信息随时可能发生变化。因此，目前对于时域反演算法的研究均为验证性仿真或试验，要求配电网参数已知，适用性较差。

当对严格相等的条件进行放宽后，该方法能达到更好的定位效果，因此文中提出改进的时域反演算法。该方法进一步扩展时域反演算法的选相特性，解决实际故障时故障类型和过渡电阻未知的问题，在10 kV含分布式电源配电网线路上进行仿真验证，并在复杂拓扑下实现良好的故障定位效果，对线路参数误差具有一定的鲁棒性。最后，在10 kV配电网线路上针对不同的过渡电阻和不同长度及参数的线路进行了现场带电试验。

1 时域反演算法原理分析

时域反演如式（1）所示。

式中:T为时间窗；s为信号；x为位置；t为时间。

时域反演变换仅仅是参考系的变换，是时间轴的拟镜像反射。为了使分析更加直观，对时域反演技术的数学建模采用频域公式推导，时域反演在频域上相当于共轭，如式（2）所示。

式中:τ=−t；ω为角频率；F［·］代表傅里叶变换；X(s)为故障信号；*代表共轭。

时域反演技术根据时域反演不变性，将时域信号进行反演处理并传回系统［19］，信号波将自动在故障源处实现时间-空间的同步聚焦。参考文献［20］，时域反演算法可以有n个信号记录装置，即端点，实际中端点一般为变电站的二次侧。在xf处发生故障，端点ri接收到故障信号，并对信号进行时域反演，在长度为L的线路上定义S1，S2，…，SM等M个猜测故障位置（guess fault location，GFL），测量时域反演信号反向注入线路上M个GFL处的信号，根据所得的M个信号的能量最大值判断故障位置。暂态信号时域反演后在故障点处实现能量聚焦的证明如式（3）所示。

式中:E为能量；G(Sk，ri，s)为Sk与端点ri之间的传递 函 数。等 式 的 成 立 条 件 为:G(Sk，ri，s)=G(xf，ri，s)。

由式（3）可以看出，故障源产生的故障信号经由端点时域反演后，在故障点处信号能量值最大，实现能量的聚焦。时域反演算法的能量聚焦特性主要与故障暂态信号传播过程及故障信号X有关，而与反演阶段GFL的故障类型、过渡电阻等设置无关，即反演阶段GFL的故障类型、过渡电阻等设置不会影响故障定位的结果。因此，可以在反演阶段针对GFL相关设置进行改进。

2 改进的时域反演算法

在对时域反演算法进行改进之前，首先对时域反演算法对高频信号的依赖进行研究。以某一无分支线路为例进行分析，在长度为L的线路xf处发生故障，故障信号为Uf(s)。变电站用一个较大的阻抗等效［19］，变电站二次侧安装一套信号记录装置。该装置将时域反演的信号反向注入传递至GFL的故障电流信号，如式（4）所示［14］。

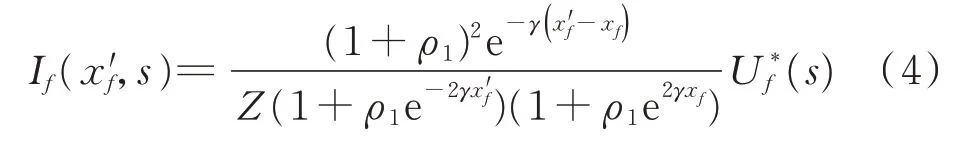
式中:Z为变电站等效的阻抗；γ为均匀传输线的传播常数；x'f代表GFL；ρ1为某端的反射系数。

利用MATLAB对时域反演算法进行仿真分析，建立了一条总长度L=10 km的线路，在xf=8 km处发生了故障。变电站等效阻抗Z=100 kΩ，采用阶跃函数来模拟故障信号Uf(s)=（1/（jω））V/（rad·s−1）。线路无损耗，单位长度电容 和 电 感 分 别 为7.10×10−12F/m和1.56×10−6H/m。每隔10 m设置一个GFL，应用式（4）计算使用单端测量时GFL处的电流，然后计算与流经每一个GFL的电流信号相对应的故障电流信号能量（fault current signal energy，FCSE），故障电流信号能量E1如式（5）所示。

式 中:xf，m代表某 个GFL；Ig(i)为xf，m处 的 故 障 电流信号Ig的第i个元素；N为矩阵Ig包含的数据量。

针对所有GFL的FCSE，以最大的FCSE为基准进行了归一化，之后的FCSE均指归一化的FCSE，如式（6）所示。

式中:m=1，2，…，M；E2(⋅)代表归一化后的FCSE。

计算结果如附录A图A1所示，图A1（a）显示了直流至1 MHz频率范围内的归一化FCSE。从图A1（a）可以清楚地看出，当GFL与实际故障位置一致时，If的能量达到最大值。当频率上限逐渐从1 MHz降至1 kHz时，时域反演算法无法定位出故障位置。因此，高频信号对时域反演算法故障定位能力贡献较大，高频信号减少会削弱时域反演算法的定位能力。

相较于无损线，线路损耗的影响主要导致线路传播的暂态信号衰减和传播速度的改变。配电网故障定位应用时域反演算法时，传播速度的改变比振幅的衰减更为关键［21］，无损线的传播速度为光速，而有损线的传播速度会降低。对于配电网故障，若反演阶段采用无损线进行计算，会导致传播速度不匹配，无法准确定位，而反演阶段采用和故障时配电网线路参数相同的有损线，传播速度相匹配，损耗的影响仅为暂态信号的衰减，而衰减后的暂态信号产生的所有贡献将在故障位置同相累加，使得故障点处积累的能量最大，从而实现准确的故障定位。

考虑总长10 km的10 kV无分支配电网针对过渡电阻不同的观测点获取的电流信号高频信号含量，使用总谐波畸变率（total harmonic distortion，THD）这一指标进行衡量。THD是指不大于某特定阶数H的所有谐波分量有效值Gn与基波分量有效值G1比值的平方和，总谐波畸变率h如式（7）所示。

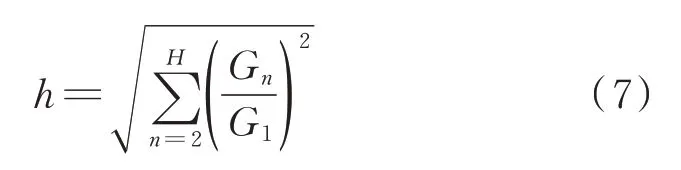
过渡电阻为0、50、100、500、1 000Ω时，THD分别 为1 373.41%、525.58%、384.98%、176.50%和124.34%。当过渡电阻值增加时，观测点获取的信号高频量明显衰减。目前，针对时域反演算法的研究中，为保证反演阶段的拓扑与故障发生时的拓扑一致，在反演阶段过渡电阻的电阻值和实际故障发生时的电阻值一致，这样处理会带来2个问题:①实际情况下电网发生故障时，过渡电阻值未知，需要采用合适的算法计算过渡电阻值［22］，故需要测量额外的参数；②当反演阶段使用相同的过渡电阻时，会造成暂态信号的二次衰减，从而对定位精度造成一定的影响。因此，当反演阶段使用接近于0的过渡电阻时，既可以避免暂态信号的二次衰减又可以避免过渡电阻的测量计算过程，提高时域反演算法的定位精度及实用性。

电力系统发生故障时，故障相较非故障相电流增大，在使用时域反演算法进行故障定位时，观测点获取的故障引起的暂态信号包含了三相电流的信号特征。根据第1章的结论，对任一故障类型，均将反演阶段GFL处的故障类型设置为三相故障。在GFL处仿真得到的三相故障电流信号保留了观测点暂态信号的特征，三相故障电流中故障相的信号能量值明显高于非故障相，具体如表1所示，从而可以实现故障定位的选相功能，使得时域反演算法在故障类型未知时得以应用。

表1 各种故障类型的选相特征Table 1 Phase selection characteristics of different fault types

改进的时域反演算法的故障定位流程如图1所示，分3步执行:①故障发生时在单个观测点记录故障产生的电磁暂态信号，并将电磁暂态信号进行时域反演处理；②人工设定GFL，获取网络拓扑和线路参数，将过渡电阻设为0，将故障类型设为三相短路，利用上述参数搭建反演阶段仿真模型；③将时域反演处理后的暂态信号反向注入网络模型中，模拟不同GFL处的电流信号，通过在仿真模型中确定与反向注入时域反演故障暂态信号相关的最大FCSE来评估故障位置。

图1 故障定位流程图Fig.1 Flow chart of fault location

3 仿真验证

3.1 选相特性

在Simulink中搭建电压等级为10 kV的配电网线路，拓扑见附录A图A2，其中0代表观测点，为变电站的二次侧，每隔1 km设置一个GFL，GFL的标号为1，2，…，16。故障类型为A相接地故障，故障发生在标号4处，在线路分支末端10和16处接有分布式电源，线路分布式参数如表2所示。其中，过渡电阻为30Ω、Z为阻抗、B为电纳。

根据现有文献的方式［17-19］，将反演阶段的过渡电阻设为与故障时相同的30Ω，与现有文献仿真模型唯一的变化是反演阶段故障类型设为三相短路，以扩展时域反演算法的选相特性。定位结果如图2所示，每个GFL有3个编号，分别代表三相。从图2中可以看出，A相的值明显高于B、C两相，因此判断为A相接地故障，并且编号为22的GFL的FCSE值最大，与实际故障位置4不相符，无法实现故障定位，仅能判断故障相。

表2 线路分布式参数Table 2 Distributed line parameters

图2 单相接地故障定位结果Fig.2 Location results of single-phase-to-ground fault

3.2 过渡电阻特性

采用3.1节的仿真模型对时域反演算法进行改进，在反演仿真阶段GFL处使用接近于0的过渡电阻，本次仿真为1×10−5Ω，则故障定位结果如图3所示。

图3 改进方法的定位结果Fig.3 Location results of improved method

与图2相比，定位在编号10处，准确定位出故障位置，并且具有选相能力。因此，实际故障发生时，使用时域反演算法进行故障定位，可以无须考虑过渡电阻的大小而在反演阶段建模时使用一个接近于0的过渡电阻即可。文中对于多种不同的过渡电阻值进行了验证，均满足这一规律。

3.3 复杂拓扑分析

考虑改进的时域反演算法对配电网复杂拓扑的适用性，参考IEEE 34节点标准系统算例的拓扑见附录A图A3，图中0为观测点、电压为10 kV，线路分布式参数如表2所示，每隔1 km设置一个GFL，A相接地故障发生在编号为21的GFL处，全长31 km，故障定位结果如图4所示。可见能准确定位出故障位置，并能实现选相功能，准确找到故障相为A相，每个GFL有3个编号，分别代表三相，其中，A相在图4中位置编号为3n−2，B相位置为3n−1，C相位置为3n，n为GFL编号，如图4所示，故障点定位至编号为21的GFL处，即图4中位置61处。改进的时域反演故障定位方法对于复杂的拓扑具有较好的适用性。

图4 复杂拓扑下的故障定位结果Fig.4 Fault location results in complex topology

时域反演算法进行故障定位需要对实际线路进行建模，但是获取的线路参数很难与实际线路的参数完全一致，存在一定的测量或计算误差，因此需要考虑该算法对于参数误差的鲁棒性。参考文献［14］和式（4），第1章中故障点与端点的传递函数G如式（8）所示。

时域反演后的故障点与端点的传递函数G∗如式（9）所示。

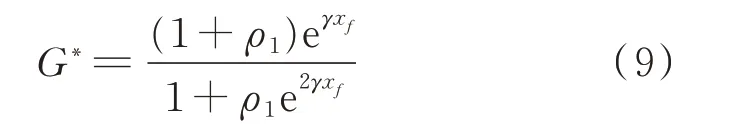
反演阶段的故障点与端点的传递函数G'如式（10）所示。

式中:ρ'1为反演阶段的反射系数，配电网线路参数不准使得其与ρ1值存在一定偏差。

如式（4）所示，GFL处的电流主要受传递函数G∗和G'的影响，变电站等效的阻抗Z和故障信号Uf(s)固定不变。将G∗和G'相乘，如式（11）所示。

考虑线路相关参数时，传播速度是一个关键参数，其在故障和反演阶段保持不变，必须保证线路长度尽可能准确，这样实际网络中可能出现的不连续的所有贡献将在实际故障位置处同相累加。第1章已证明，在x'f=xf时信号能量值最大，将x'f=xf代入式（11），如式（12）所示。

采用第2章的数据，考虑ρ'1=(0.8～1.2)ρ1，所得结果如附录A图A4所示。无损线路ρ'1的误差变化对于传递函数大小的影响很小，图中红点为反演阶段对ρ1的无误差估计的结果。

对于有损线路，考虑附录A图A3所示的复杂配电网拓扑结构，将故障类型设为A相接地，人工将线路参数误差设置为5%，所得结果如图5所示。改进的时域反演故障定位方法仍能保证很好的定位效果，并具有选相功能，故障相为A相，故障点定位至编号 为21的GFL处，即图5中位置61处，与 实际相符。

图5 考虑参数鲁棒性的故障定位结果Fig.5 Fault location results considering parameter robustness

4 现场试验

在中国长沙市进行了现场试验，所开发的故障定位系统如附录B图B1所示，可分为测量单元、数据获取单元、故障定位单元3个部分。测量单元基于自研的宽频电磁传感器用以测量故障引起的暂态信号（见图B2），传感器为无源传感器，输出信号为模拟信号，分别安装在故障相和非故障相。

数据获取单元主要通过示波器完成，将传感器输出的信号进行A/D转换，所用示波器型号为Tektronix MDO4054-3，带宽为500 MHz，上升时间为700 ps，采样率为每秒采集2.5×109个点。利用故障发生时电流幅值突然增大的原理采用边沿触发获取故障发生时的暂态信号。数字示波器装置自身具备通用串行总线（USB）接口，可连接U盘将数据以CSV格式存储。将CSV文件存储的波形数据采用自适应滤波算法去除工频信号，该滤波算法可提高定位精度，经时域反演后作为信号源在仿真模型进行仿真定位。

试验线路的供电示意图如附录B图B3所示，传感器安装在断路器2S01右侧，即变压器的二次侧，在杆塔3-4处设有隔离开关，用以接入10 kV接地试验电阻柜，如附录B图B4所示。每个绿管电阻值为2 kΩ，通过对电阻的串并联实现多种接地电阻，线路连通接地电阻后经过三相开关与地线相连，本次试验所用的接地电阻为200Ω。

如附录B图B3所示，首先合上断路器370和断路器380，再合上隔离开关3361和336A，故障类型为A相接地故障。然后将电压升为10 kV后，连接隔离开关3041给架空线路通电，通电一段时间使电压保持稳定后连接隔离开关3341，A相接地故障状态保持2 s。最后断开隔离开关3341，切断A相接地故障，降压后将试验线路断电复原。所得波形如图B5所示。

将附录B图B5所示的信号数据导入工控机中基于改进的时域反演算法进行故障定位，GFL的定义为:断路器2S01右侧安装传感器，编号为0，之后每1 km定义一个GFL，故障位置在5 km处，编号为13、14和15（对应A、B、C三相）。所得的故障定位结果如图B6所示，可以看出，虽然相比于前述的仿真结果精度有所下降，但是仍能准确定位出故障位置，B、C相数值相同是因为测量时考虑绝缘问题，配电柜空间较小，三相线距离较近，传感器距离过近可能会在高电压下绝缘击穿，因此非故障相只测一相，实际上B、C相数值本身差别也不大。

考虑200、500、1 000Ω三种过渡电阻，并在杆塔1-4处接入2 km的地下电缆，考虑架空线路和地下电缆混合的情况，所得结果如表3所示。从表3可以看出，各种情况下均能准确定位出故障相，并且定位精度均在300 m以内，而过渡电阻值的增大和线路混合会降低故障定位的精度。

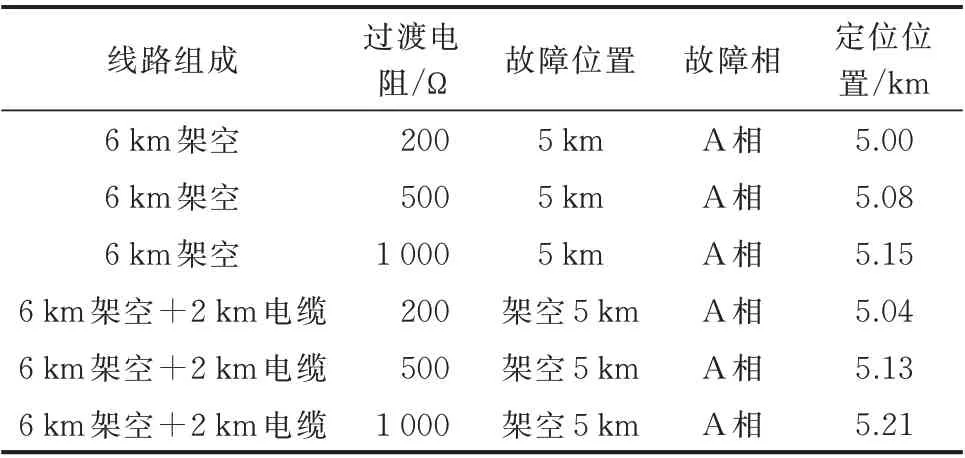
表3 试验定位结果Table 3 Location results of test

5 结语

本文通过对时域反演算法实现故障定位的原理进行分析，反演阶段GFL处故障类型、过渡电阻等设置不会影响故障定位的结果。信号的高频量对时域反演算法定位性能影响较大，过渡电阻对信号的高频量具有衰减作用，因此反演阶段使用接近于0的过渡电阻既可以省去获取过渡电阻值的过程又可以提高定位精度。在反演阶段采用三相短路故障类型，可以实现时域反演算法故障定位的选相功能，并使得时域反演算法能在故障类型未知时得以应用。改进的时域反演故障定位方法对于长线路、复杂拓扑的配电网具有较好的故障定位效果，并且具有良好的参数鲁棒性。本文将改进的时域反演算法应用于实际的配电网，并对试验过程进行了详细的说明，综合考虑200、500、1 000Ω三种过渡电阻及6 km架空线路、6 km架空线路和2 km地下电缆混合的情况，结果表明改进的时域反演算法均能实现故障定位，定位误差均小于300 m。

本文解决了时域反演算法中故障类型和过渡电阻未知的问题，并扩展其选相特性。但是所改进的时域反演算法仍然需要获取网络拓扑和线路参数，网络的基本拓扑可以从地理信息系统（GIS）等获取，从数据采集与监控（SCADA）等系统获取线路中开关状态等信息以获取线路实时拓扑，而线路的数据可以从台账等系统获取，随着能量管理系统（EMS）、微型相量测量单元（PMU）等系统的发展，为本文所提方法提供了数据基础。下一步将结合配电网的信息系统开展进一步研究，以提高配电网模型参数的准确性，进而提高所提方法的实用性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。