英美早期代数教科书中的函数概念

刘思璐，沈中宇，汪晓勤

英美早期代数教科书中的函数概念

刘思璐1，沈中宇2，汪晓勤1

（1．华东师范大学教师教育学院，上海 200062；2．苏州大学数学科学学院，江苏 苏州 215006）

针对函数概念，对1810—1969年间出版的216种英、美代数教科书进行考察．研究发现，按照时间顺序，分别出现了函数的“表达式”“变量依赖关系”“变量对应关系”“集合对应关系”“序偶集”5类定义．其演变规律既受函数概念本身历史发展的影响，也和数学教育的发展有关．早期教科书中函数概念的演变过程和演变原因为今天培养学生核心素养、理解学生认知障碍和改善函数课堂教学提供了重要启示．

函数概念；早期教科书；定义；演变；数学教育史

1 问题提出

《高中数学课程标准（2017年版）》指出：“函数是现代数学最基本的概念，是描述客观世界中变量关系和规律的最为基本的数学语言和工具，在解决实际问题中发挥重要作用．函数是贯穿高中数学课程的主线．”[1]发展学生数学核心素养是数学课程的重要目标，函数概念的历史发展过程是一个逐渐抽象的过程，该过程可以为学生数学抽象素养的培养提供借鉴．此外，教学中呈现函数概念的演进历史，有助于让学生树立动态的数学观，认识数学和数学活动的本质，感悟数学背后的理性精神．教学实践与实证研究表明，由于函数概念的抽象性，学生学习函数概念时存在一定的困难，学生的函数概念意象与函数定义存在分离现象[2]，学生对函数的理解呈现出一定的历史相似性，故历史上函数概念的认识论障碍有助于教师更好地理解学生的认知障碍[3]．同时，高中函数概念教学中，需要揭示初中数学中的变量说定义的局限性以及新的对应说定义的必要性[4]，借鉴历史，有助于改善函数概念的教学．

关于函数概念的历史，一些学者先后进行了较为深入的研究[5-7]，这些研究呈现了函数概念较为清晰的演进脉络．但是，迄今为止，除个别文献外[8]，很少见到函数概念教育史方面的深入研究．不同时代的教科书中所呈现的函数概念，反映了当时教科书编写者对函数概念的理解，也反映了函数概念在数学课程中的历史演变规律，同时蕴含着教科书编写者的教学经验与智慧，为今日课程与教学提供诸多启示．在西方早期代数教科书中，英、美两国是早期教科书资源较为丰富并较早教授函数概念的国家，且对中国数学教育影响较大，故这里聚焦英、美早期代数教科书．通过对1810—1969年间出版的英、美代数教科书中有关函数概念内容的考察，试图回答以下问题：早期代数教科书是如何定义函数的？随着时间的推移，定义又是如何演变的？演变的动因是什么？

2 研究对象

选取216种英、美代数教科书作为研究对象．以20年为一段，各教科书的时间分布情况如图1所示．对于同一作者再版的教科书，若内容无变化，则只采用最早的版本，若内容有变化，则将其视为不同教科书[9]．

图1 216种教科书的时间分布

216种代数教科书中，126种为中学教科书，90种为大学教科书．函数定义所在章节大致可以分为“定义”“变量”“方程”“函数”“微积分”“函数与方程”“其它（如引言、最大值和最小值、集合等）”7类，表1为章节分布情况（若教科书中有多个章节出现函数定义，则统计第一次出现的章节），其中“函数”章占比最高．

表1 函数概念在216种代数教科书中的章节分布

图2为含函数定义的章节在各时间段的分布情况．从中可知，在19世纪的教科书中，很少出现聚焦函数的独立章节，函数远未成为“主角”；一般仅在“定义”“方程”等起始章或“其它”章节中作简单介绍．到了20世纪，函数定义大多出现在“变量”“函数”“函数与方程”这几章，可见，函数概念逐渐从幕后走向台前；直到1950年，函数俨然已经成为教科书的重点．1830—1949年间的每个时间段中，“方程”或“方程与函数”章都占有一定比例，可见这个时期的教科书编写者认为函数与方程关系密切．

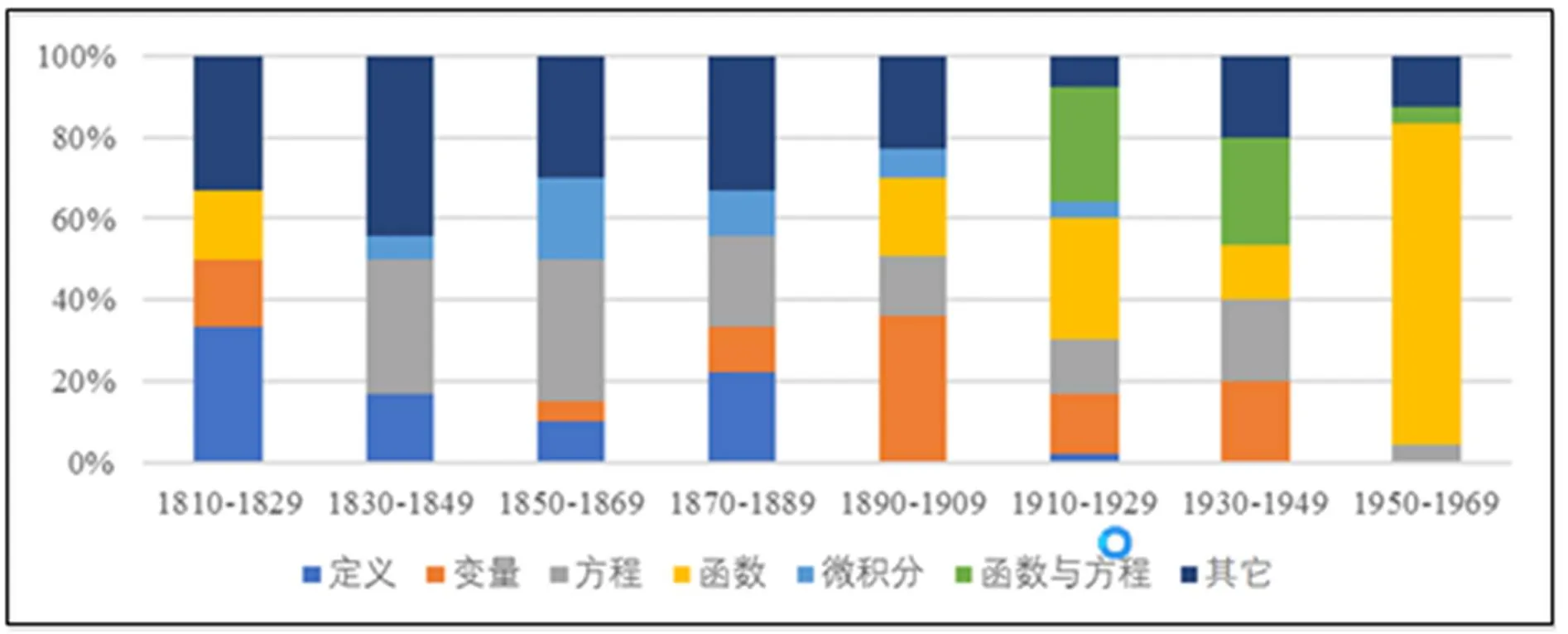
图2 216种教科书中函数在每个时间段各章节中的分布

采用的统计方法如下：第一步，按照年份查找并摘录出研究对象中的函数定义及其相关内容；第二步，通过参考已有的函数概念史文献和研究成员讨论，制定以关键词为参照的一级分类指标，再由两位研究者根据分类标准对函数定义分别进行分类与统计，对分类结果不一致的定义（主要是混合型定义）再进行讨论，改进一级分类指标重新统计；第三步，对每一类函数定义进行关键词和性质提取，讨论并形成二级分类指标，再由两位研究者进行分类统计并检验．

3 函数定义的分类

216种教科书中共有222个函数定义，其中4种教科书在不同章节给出两个不同的定义，一种给出3个不同定义．根据定义中的关键词和性质[6]，222个定义可分为“表达式”“变量依赖关系”“变量对应关系”“集合对应关系”“序偶集”5类，依次占40.5%、42.3%、8.6%、4.5%和4.1%．

3.1 “表达式”定义

“表达式”定义源于18世纪约翰·伯努利（J. Bernoulli，1667—1748）和欧拉（L. Euler，1707—1783）的定义[6]．共90种教科书采用了此类定义，又可分为“组合型”“包含型”“依赖型”“对应型”4种．

3.1.1 组合型

采用“变量与常量组合而成的表达式”的定义称为“组合型”定义，为欧拉原始的陈述方式．表2给出了“组合型”定义3种形式的典型例子，从中可知这类定义涵盖了多元函数的情形，并且19世纪初期人们对于“未知量和变量”“已知量和常量”的使用有所混淆．

3.1.2 包含型

采用“包含量（或）的表达式”的定义称为“包含型”定义．表3给出了“包含型”定义3种形式的典型例子．这类定义大多局限于一元函数．

3.1.3 依赖型

采用“依赖于量（或）的表达式”的定义称为“依赖型”定义．这种定义已有“变量依赖关系”定义的雏形，一方面再现了18世纪“表达式”定义向“变量依赖关系”定义过渡的倾向性，另一方面也反映了教科书作者虽受欧拉“变量依赖关系”定义的影响，但更倾向于“表达式”定义的心态．表4给出了“依赖型”定义的典型例子，查阅书中例子，该定义也涵盖多元函数的情形．

表2 “组合型”定义的典型例子

表3 “包含型”定义的典型例子

表4 “依赖型”定义的典型例子

3.1.4 对应型

在采用“表达式”定义的教科书中，只有Milne这样定义函数：“对于的不同值，有不同的值与之对应的表达式称为的函数．”[22]该定义反映了作者虽受狄利克雷（G. L. Dirichlet，1805—1859）“变量对应关系”的影响，却更倾向于“表达式”定义的心态．但定义中的“对应”乃是建立在表达式的基础之上，迥异于狄利克雷定义中的“对应”（可以是任意的）．

3.1.5 变化趋势

以上4种定义依次占“表达式”定义总数的8.9%、44.4%、45.6%和1.1%．图3给出了这4种定义的时间分布情况．

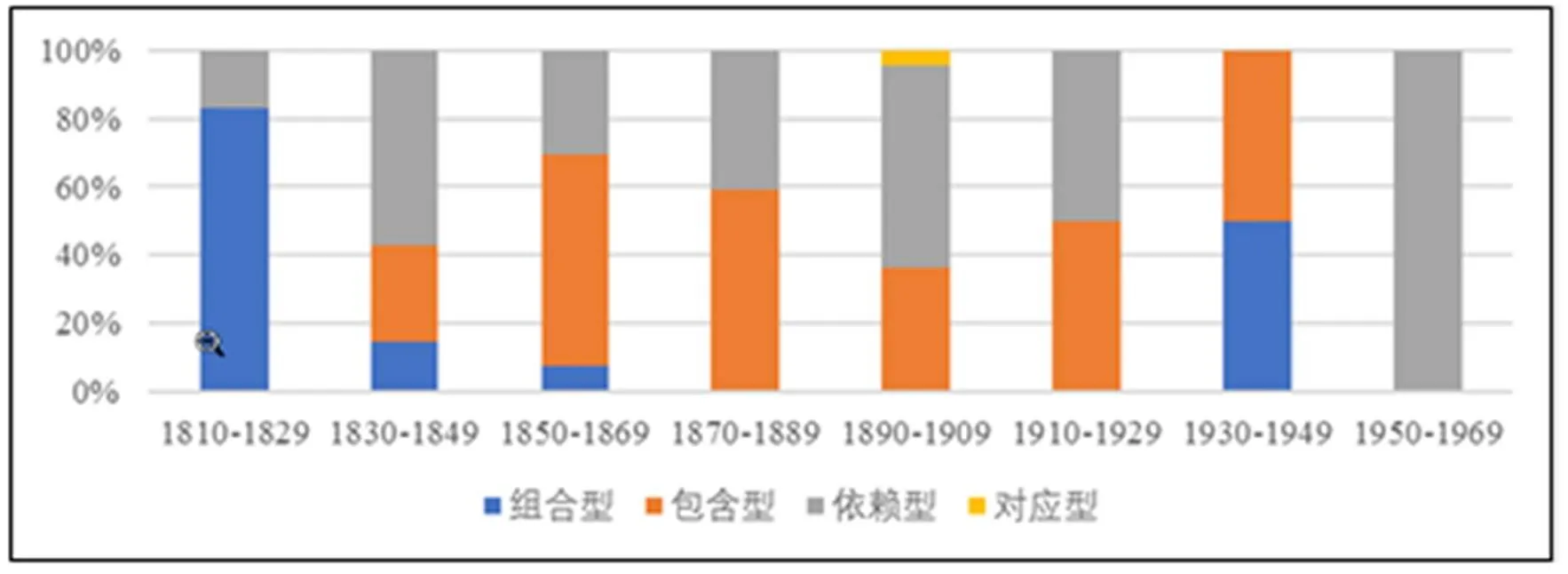
图3 4种“表达式”定义的时间分布

由图3可知，19世纪初期，“组合型”定义占统治地位，“依赖型”定义和“包含型”定义则是19世纪中后期的主流．“对应型”定义在20世纪初昙花一现．20世纪中叶以后，“依赖型”定义一枝独秀．这表明，“表达式”定义受到了“变量依赖”定义的影响，到20世纪中叶，已呈现向“变量依赖关系”定义过渡的趋势．

3.2 “变量依赖关系”定义

“变量依赖关系”定义源于欧拉1755年在《微分基础》中的定义．共94种教科书采用了该类定义，可进一步分为“依赖型”“应变型”“定值型”“并举型”4种[6]．

3.2.1 依赖型

采用“依赖于其它量的变量”的定义称为“依赖型”定义，最早见于1830年的教科书，是“变量依赖关系”定义中最早出现的一种．表5给出了“依赖型”定义的典型例子，从中可知，“依赖型”定义适用于一元函数和多元函数，且书中的例子包含了单值函数和多值函数．此外，从表5可见，当时存在着量与数混用的现象．

3.2.2 应变型

采用“随其它量的变化而变化的量”的定义称为“应变型”，最早见于1852年，晚于“依赖型”．如Wentworth将函数定义为：“若两个变量关系如下，即一个变量的值的变化会导致另一个变量的值的变化．则其中一个变量被称为另一个变量的函数．”[27]Nicholson将函数定义为：“当变量与变量关系如下，即值的任何变化都会导致值的变化，则称为的函数．”[28]这种定义仅涉及一元函数和单值函数．

3.2.3 定值型

采用“由其它量的值所确定的变量”的定义属于“定值型”，最早见于1889年，在“变量依赖关系”定义中出现最晚．表6给出“定值型”定义的典型例子，此种定义仅涉及一元函数．

表5 “依赖型”定义的典型例子

表6 “定值型”定义的典型例子

3.2.4 并举型

“并举型”指的是“依赖型”“应变型”“定值型”中的某两类的组合以及“依赖+对应”形式，其中“依赖+应变”数量最多．表7为“并举型”定义的典型例子，从中可见诸定义既适用于单值函数，又适用于多值函数，但仅涉及一元函数．

3.2.5 变化趋势

上述4种定义依次占“变量依赖关系”定义总数的68.1%、7.4%、8.5%和16.0%．图4给出了4种“变量依赖关系”定义的时间分布情况．

表7 “并举型”定义的典型例子

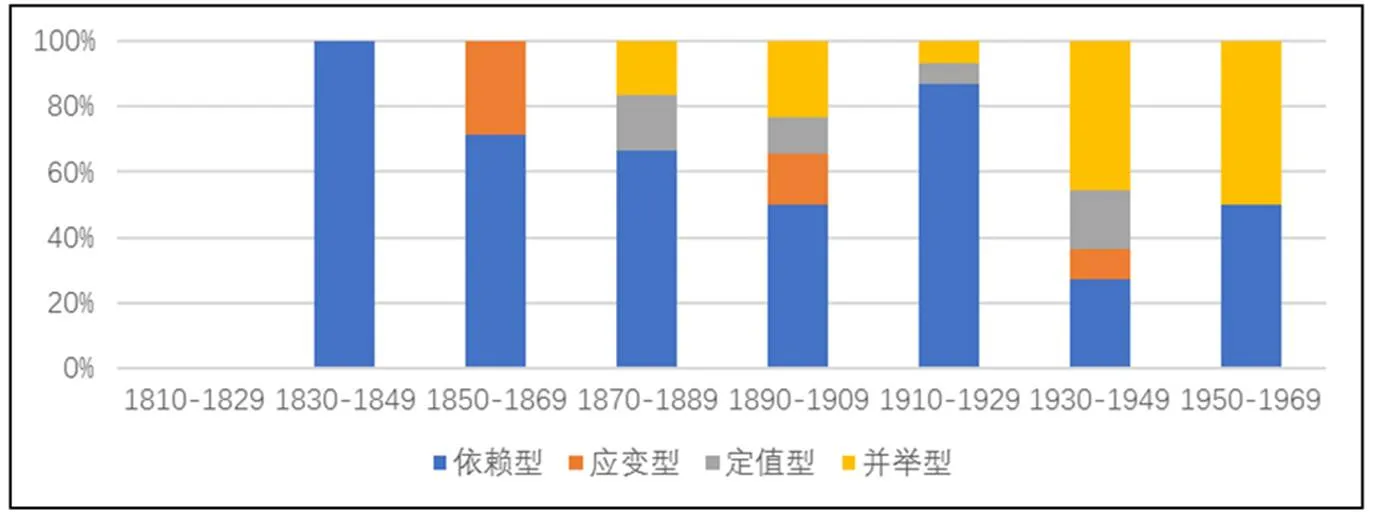
图4 4种“变量依赖关系”定义的时间分布

由图4可知，直到1830年才出现“变量依赖关系”定义，且以“依赖型”为主，到了19世纪中叶出现“应变型”，后来又出现了“定值型”和“并举型”，但一直以“依赖型”为主流，直到20世纪中叶“并举型”才逐渐成为主流．这表明，早期人们对于函数存在依赖关系的认识根深蒂固，而到了后期随着函数定义内涵与外延的扩展，人们的认识也逐步加深，故“并举型”成为主流．

3.3 “变量对应关系”定义

“变量对应关系”定义源于狄利克雷1837年的函数定义．只有19种教科书采用了这类定义，进一步又分为“无变化范围的变量对应”和“在变化范围内的变量对应”两种．

3.3.1 无变化范围的变量对应

这种定义指的是：“若第二个变量的值与第一个变量的值对应，则第二个变量是函数．”表8给出了无变化范围的变量对应的典型例子，从中可见诸定义既涵盖了单值函数也涵盖了多值函数，但仅局限于一元函数，其中的两种形式也表明当时人们对变量与数的混淆．

3.3.2 在变化范围内的变量对应

此种定义较之于前一种，增加了变量的取值范围．表9为该类定义的典型例子，从中可见，这些定义先是逐步规定了自变量的取值范围，到了1911年，有的教科书又加入因变量的取值范围．这种对变量规定取值范围的思想，为后来的“集合对应”定义提供了启示．

表8 无变化范围的变量对应的典型例子

表9 在变化范围内的变量对应的典型例子

3.4 “集合对应关系”定义

“集合对应关系”定义（即所谓的“对应说”）源于布尔巴基学派的《数学基础》．有10种教科书采用了此类定义，可分为“集合之间的映射”和“集合之间的对应关系”两种形式，其典型例子见表10，从中可知，这类函数定义仅涉及单值函数．

3.5 “序偶集”定义

“序偶集”定义源于布尔巴基学派的《数学基础》．有9种教科书采用这类定义，可分为“笛卡儿积”“有序对”“关系”3种形式，其典型例子见表11．

“序偶集”定义强调函数的单值性，Brumfiel（1961）用“母子关系”生动形象地说明了这一点：“函数是一种关系，该关系中没有两个有序对具有相同的第一个元素．如在所有人的集合中，关系‘是的母亲’是一个函数．关系‘是的儿子’不是函数．”[49]母亲是唯一的，但一个母亲可以有一个或多个儿子．

4 函数定义的演变

函数的以上5类定义以及每类定义的各种表述形式是在漫长的历史长河中逐渐产生的．以20年为分布单位，图5给出了5类定义的时间分布情况．从图5中可见，19世纪函数概念以“表达式”定义为主，后来“变量依赖关系”定义逐渐流行．“变量对应关系”定义主要出现在20世纪上半叶的教科书中，但数量不多．到了1950年代，“集合对应关系”和“序偶集”定义后来居上，占据了统治地位．

表10 “集合对应关系”定义的典型例子

表11 “序偶集”定义的典型例子

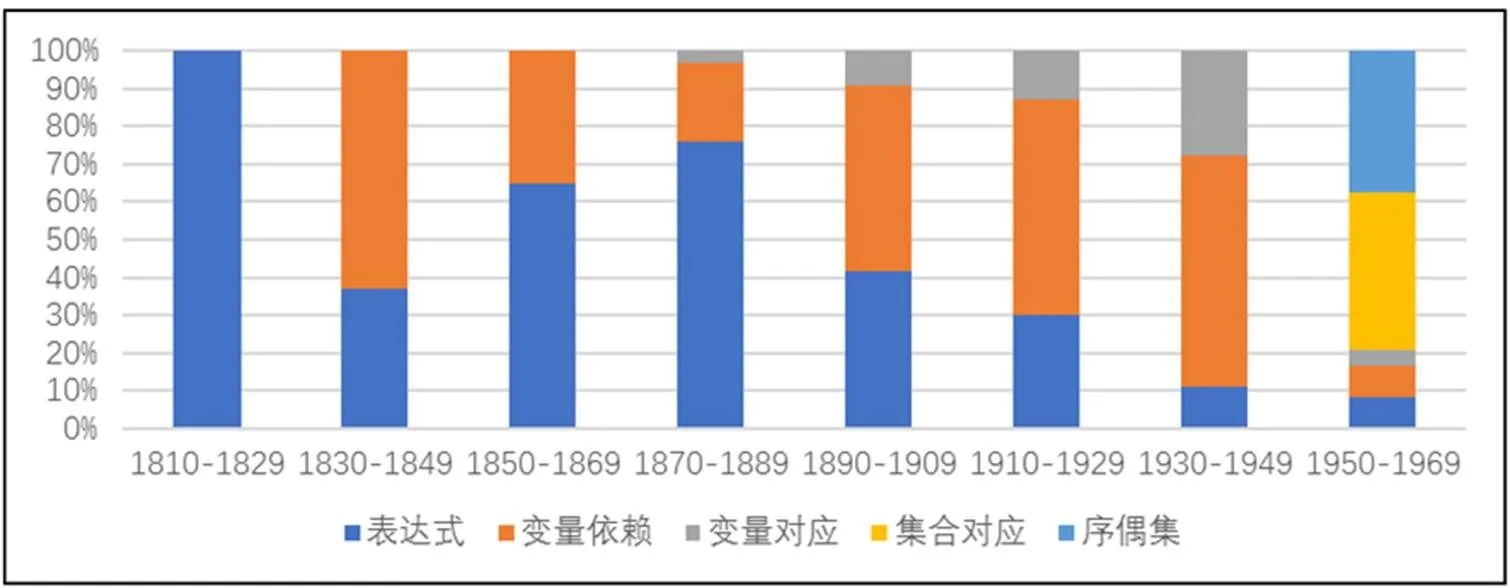
图5 216种教科书中函数5类定义的时间分布

其次，教科书中函数定义的演变中有一些内涵和外延的变化也是值得注意的．主要有以下几个方面．

（1）从“变量”或“数”的角度来定义函数．19世纪有一些教科书用“数的变化”来定义函数，反映的是当时人们对于变量的认识不够充分，没有彻底区分数与变量．从数到“变数”，再到区分常量与变量，体现了数学定义从不严谨到严谨的发展过程．

（2）从“变量”到“对应关系”．“表达式”“变量依赖关系”“变量对应关系”定义明确表示函数是变量．而“集合对应关系”和“序偶集”定义则将函数视为“对应关系”．这种转变体现了教科书编写者对函数概念认识的加深．

（3）从多元函数到一元函数．总的来看，19世纪初教科书中的“表达式”和“变量依赖关系”定义都包含了多元函数，而19世纪末及以后的“变量对应关系”“集合对应关系”“序偶集”定义则聚焦一元函数．

（4）从多值函数到单值函数．19世纪教科书编写者从方程角度定义和理解函数，故“表达式”“变量依赖关系”“变量对应关系”定义并不要求函数的单值性，有的定义明确提到了“一组函数值”．到了20世纪中叶，“集合对应关系”和“序偶集”定义明确要求函数的单值性．

5 函数定义演变的动因

英、美早期代数教科书中函数定义的演变经历了两个世纪，主要受到函数概念本身的历史发展和数学教育发展的

影响．

5.1 函数概念的发展

从数学知识内部来看，函数概念本身的发展对教科书中函数定义有着根本性影响．1748年，欧拉在《无穷分析引论》中用“变量与常量任意组成的解析式”来定义函数[50]．到了1755年，欧拉又在《微分基础》中用“依赖于其它变量的变量”重新定义函数[51]．1837年，狄利克雷在“用正弦和余弦级数表示完全任意的函数”一文中提到，不论是否存在数学上的运算关系还是变量之间的依赖关系，只要两个变量存在对应的变化，因变量就是函数，从而拓展了当时的函数概念[52]．

直到1939年，布尔巴基学派在《数学基础》一书中用“两个集合之间的单值对应关系”来定义函数，此书提到函数是一种单值映射，并论述了与序偶集的关系[54]．据此，可得到图6，即函数概念史（上面的）和教科书中函数定义类型（下面的）的对比图，其中“解析式”原英文为“analytic expression”，“表达式”原英文为“expression”．

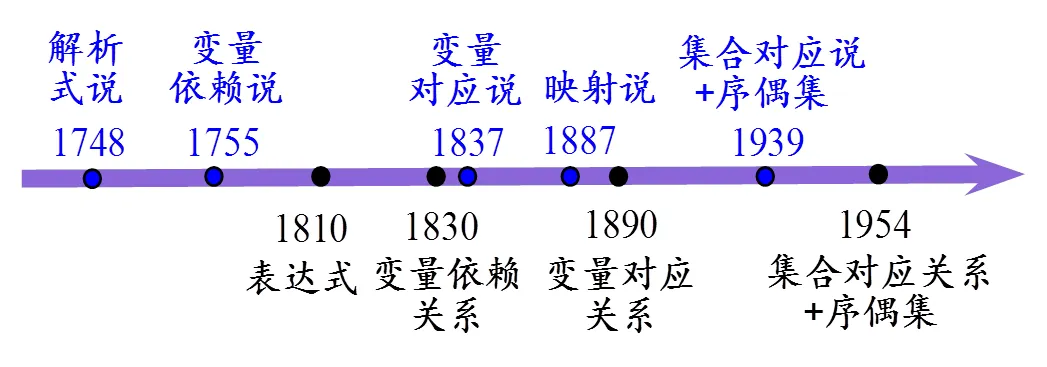
图6 函数概念史和教科书中函数定义类型对比

通过对比可知，早期代数教科书中的5类定义皆源于历史上的各种定义，但存在滞后现象，即教科书中每类函数定义出现的时间滞后于历史上该类定义出现的时间．这其中不乏数学知识传播的时间差原因，也与人们在函数概念理解上的困难和以欧拉为代表的权威数学家定义函数概念的巨大影响息息相关．

5.2 数学教育的发展

从数学外部环境来看，数学教育发展对教科书中函数概念的定义和传播也有着显著的影响．接下来将从19—20世纪的代数教学史和英美两国的数学教育史进行探讨．

5.2.1 代数教学史

19世纪起，代数作为一门独立的课程在中等教育课程中得以确立．20世纪则是代数教学的巅峰和衰落的世纪[55]．其中，培利—克莱因数学教育改革运动和数学教育现代化运动对教科书中函数内容影响较大．

函数是一个在数学内外都有着许多应用的概念．1901年，英国数学家培利（J. Perry，1850—1920）在其演讲中提出了一套新的实用数学课程[55]．之后德国数学家克莱因（F. Klein，1849—1925）在其名著《中等学校的数学教育讲义》（1907）和《高观点下的初等数学》（1908）提出以函数概念统一数学教育内容的思想，在这种改革思想的影响下，各国新的一批中学数学教科书相应地问世，函数概念也成为了各国中学数学中举足轻重的内容[56]．这从某种程度上解释了20世纪初期研究对象较多，至于20世纪上半叶的教科书中函数定义更青睐于选择“变量依赖关系”定义的原因，之后将从英、美两国数学教育史讨论．

1958年，数学教育现代化运动开始，各国新的大纲与教材都提到要对中学数学内容进行结构化、公理化和现代化等的改革，以集合—关系—映射—运算—群—环—域—向量空间的代数结构为主轴，统一中学数学内容．此次运动对20世纪60年代英、美中学数学产生了深远的影响，使得函数和群、集合等大学数学知识进入中学数学教育[56]．可见数学教育现代化运动促进了代数教科书中从集合、映射、笛卡儿积的角度来定义函数．

5.2.2 英国教育史

19世纪初，中学教育主要由公立学校、文法学校和私立学校提供．数学在课程中并不占显著地位且不能随意教授[55]．这也从一方面解释了，为什么19世纪前叶的研究对象较少且教科书中函数定义滞后于历史上的函数概念．19世纪后半叶，随着新型中学的出现以及军官选拔的要求，数学在课程设置中逐渐占有重要的地位．同时，高质量的数学老师和他们编写的教科书对整个中学数学教学部门产生了相当大的影响．数学家德摩根等人也意识到如果英国想要在工业和经济上继续进步，那么数学知识就必须变得更加普及[55-57]．故此，这个时期教科书中函数的定义开始青睐于实际生活中更加相关的“变量依赖关系”定义．

到了20世纪，中学数学课程内容是由大学入学要求和各大学考试委员会的教学大纲决定．这意味着很多学校都开始为大学做准备[55]．那时的大学考试有一道题目是“定义一个函数并且证明每个函数都有导数”．1912年的一份报告给出了当时几乎所有的学校都会教函数图象表征等内容的结论，并称当时英国的数学教育取得了“显著的进步”[57]．可见函数内容在中学教学中已经不可或缺，也解释了为何到了20世纪之后教科书中的函数定义不再青睐“表达式定义”，而是倾向于抽象程度更高的函数定义．而到了20世纪60年代，“集合的语言”和“关系、映射与函数”俨然已经成为教科书中的主题[55]．所以，此时的教科书中的函数定义多为“集合对应关系”定义和“序偶集”定义．

5.2.3 美国教育史

19世纪初，一些法国的代数教科书输入美国作为教材，如欧拉的《初等代数》．直到19世纪30年代以后，美国数学家开始结合本国实际编写本国教科书[56]．到了19世纪中叶，西点军校的数学教授戴维斯（C. Davies）的《初等代数》这本书比较成功[55]．查阅这两本教科书中的函数定义，分别是“表达式”定义和“变量依赖关系”定义，结合19世纪上半叶美国的数学教育方兴未艾，这也解释了这段时间教科书中定义的分布情况．

1907年，美国数学教育家杨格（J. W. A. Young）在《中小学数学教学》提到，函数思想描述的是一个变量对另一个变量的依赖[58]．1921年美国全国数学教委会的报告《中学数学中的函数概念》和数学教育家哈斯勒（O. Hassler）等的《中学数学的教学》中都明确提到，教师与数学家愈来愈认识到，函数关系是建立代数课程的最佳的统一概念，他们期望通过大量的实例来培养学生的函数思想，让学生理解函数是变量之间的依赖关系，而函数理论与函数的“正式定义”甚至不必出现[59-60]．1923年全国数学要求委员会发表了《中学教育中的数学重构》这一报告，明确要求学生能表示和理解一个变量对另一个变量的各种依赖关系[61]．由此可知，“变量对应”定义之所以对早期教科书的影响并不大，是因为那时的数学教育家需要在函数定义的严谨性和可学性之间寻找平衡的缘故，变量依赖关系毕竟比变量对应关系更易于被学生所理解．

6 结论与启示

对于函数概念，1810—1969年间出版的216种英、美教科书中，按时间先后顺序，共出现了“表达式”“变量依赖关系”“变量对应关系”“集合对应关系”“序偶集”5类定义．但即使到了20世纪五、六十年代，“集合对应关系”和“序偶集”定义占据主导地位，其它类型的定义并没有因此销声匿迹，可见“表达式”和“变量依赖关系”定义影响深远．相比而言，“变量对应关系”定义对早期教科书的影响较小．这一演变规律既受函数概念本身的影响，也和数学教育的发展息息相关．

根据以上研究结论，得到以下启示．

（1）培养学生核心素养．早期教科书中的函数概念经历了从“表达式”定义到“变量依赖关系”定义，再到“变量对应关系”定义，又到“集合对应”定义，最后到“序偶集”定义的过程，其中蕴含了从具体的表达式到抽象的序偶集的数学抽象过程．历史是一个坐标系，有助于人们更清晰地认识函数概念的数学抽象素养水平，从而在函数教学中进一步落实数学核心素养．

（2）理解学生认知障碍．尽管20世纪已有“序偶集”函数定义，仍有教科书采用“表达式”“变量依赖”等定义，这反映了函数是解析式、函数要有依赖关系在人们的心中是根深蒂固的，这与现在大多数学生对于函数的意象是一致的，为今天的函数教学提供了参考．其次，数与变量的区分不仅是历史上人们容易混淆的难点，也是现在中学生对于函数概念的认知难点之一，对于变量本身的理解，应该成为学生认识函数的重要前提．

（3）改善函数课堂教学．如何帮助学生进一步扩展函数理解是高中函数概念教学的一个难点．从函数定义的演变中可以看出有依赖型的“表达式定义”以及定值型的“变量依赖关系”，在课堂中可以借助这些混合型的定义，帮助学生自然地完成从表达式定义到变量依赖定义再到变量对应关系的过渡．可以借鉴早期教科书中逐步引入变量的取值范围再到用集合代替取值范围，来帮助学生转变从初中函数是因变量到高中函数是集合对应关系的理解．同时，可以让初中学生从“变量对应”角度和高中学生从“集合对应”角度认识并理解函数的“单值性”和“一元性”及其原因．

[1] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：18-19．

[2] VINNER S. Concept definition, concept image and the notion of function [J]. International Journal of Mathematical Education in Science & Technology, 1983, 14 (3): 293-305.

[3] 任明俊，汪晓勤．中学生对函数概念的理解——历史相似性初探[J]．数学教育学报，2007，16（4）：84-87．

[4] 邓勤．新课程背景下初高中数学教学的有效衔接——从函数概念的教学谈起[J]．数学通报，2011，50（2）：33-35．

[5] 杜石然．函数概念的历史发展[J]．数学通报，1961，1（6）：36-40．

[6] 汪晓勤．19世纪中叶以前的函数解析式定义[J]．数学通报，2015，54（5）：1-7，12．

[7] 李鹏奇．函数概念300年[J]．自然辩证法研究，2001，17（3）：48-52．

[8] 关嘉欣，汪晓勤．19世纪末20世纪初美国初等代数教科书中的函数概念[J]．数学通报，2015，54（11）：10-14．

[9] 栗小妮，汪晓勤．美国早期教科书中的无理数概念[J]．数学教育学报，2017，26（6）：86-91．

[10]  EULER L, LAGRANGE J L. Elements of algebra [M]. London: Printed for J. Johnson and Co., 1810: 248.

[11]  BONNYCASTLE J. A Treatise on algebra [M]. London: J. Johnson & Co., 1813: 8.

[12]  LEWIS E. A treatise on algebra [M]. Philadelphia: Kimber and Sharpless, 1826: 97.

[13]  De MORGAN A. The elements of algebra [M]. London: John Taylor, 1835: 168.

[14]  TODHUNTER I. An elementary treatise on the theory of equations [M]. London: Macmillan & Co., 1875: 2.

[15]  HACKLEY C W. A treatise on algebra [M]. New York: Harper & Brothers, 1846: 143.

[16]  DODD J B. Algebra for high schools and colleges [M]. New York: Pratt, Oakley & Co., 1860: 223.

[17]  RAY J. Algebra (part II) [M]. Cincinnati: Sargent, Wilson & Hinkle, 1852: 341.

[18]  MILNE W J. Academic algebra [M]. New York: American Book Company, 1901: 378.

[19]  ROBERTSON W J, BIRCHARD I J. The high school algebra [M]. Toronto: W. Briggs, 1886: 238.

[20]  TAYLOR J M. A college algebra [M]. Boston: Allyn & Bacon, 1889: 7.

[21]  WENTWORTH G A. A college algebra [M]. Boston: Ginn & Co., 1888: 384.

[22]  MILNE W J. Standard algebra [M]. New York: American Book Co., 1908: 347.

[23]  SMYTH W. Elements of algebra [M]. Portland: Shirley & Hyde, 1830: 347.

[24]  DAVIES C, BOURDON M. Elements of algebra [M]. New York: Wiley & Long, 1835: 241.

[25]  OLIVER J E, JONES G W, WAIT L A. A treatise on algebra [M]. Boston: Ginn, Heath, & Co., 1882: 19.

[26]  SWENSON J A. High school mathematics [M]. New York: Macmillan, 1923: 275.

[27]  WENTWORTH G A. A college algebra [M]. Boston: Ginn & Co., 1899: 313.

[28]  NICHOLSON J W. School algebra [M]. New York: American Book Co., 1909: 257.

[29]  BIRCHARD I J, ROBERTSON W J. The high school algebra: Part II [M]. Toronto: W. Briggs, 1889: 21.

[30]  ATWOOD G E. Standard school algebra [M]. New York: The Morse Co., 1898: 360.

[31]  SKINNER E B. College algebra [M]. New York: The Macmillan Co., 1917: 49.

[32]  NEWCOMB S. Algebra for schools and colleges [M]. New York: H. Holt, 1884: 28.

[33]  HALLETT G H, ANDERSON R F. Elementary algebra [M]. Boston: silver, Burdett & Co., 1917: 255.

[34]  HARDING A M, MULLINS G W. College algebra [M]. New York: The Macmillan Co, 1928: 135.

[35]  ROUSE L J. College algebra [M]. New York: J. Wiley & Sons, 1931: 162.

[36]  FISHER G E, SCHWATT I J. Elements of algebra [M]. New York: The Macmillan Co., 1899: 418.

[37]  DICKSON L E. College algebra [M]. New York: J. Wiley & Sons, 1902: 76.

[38]  WELLS W, HART W W. Second course in algebra [M]. Boston: D. C. Heath, 1913: 277.

[39]  FINE H B. The number-system of algebra [M]. Boston: Leach, Shewell & Sanborn, 1890: 66.

[40]  RIETZ H L, CRATHORNE A R. College algebra [M]. New York: Henry Holt and Co, 1909: 26.

[41]  YOUNG J W, MITCHELL U G, DENTON W W. Lectures on fundamental concepts of algebra and geometry [M]. New York: The Macmillan Co., 1911: 192-193.

[42]  KNEBELMAN M S, THOMAS T Y. Principles of college algebra [M]. New York: Prentice Hall, inc., 1942: 254.

[43]  ARTIN E. Selected topics in modern algebra [M]. Carolina: Chapel Hill, 1954: 3.

[44]  School Mathematics Study Group. Mathematics for high school [M]. New Haven: Yale University Press, 1959: 513.

[45]  MILLER I, GREEN S. Algebra and trigonometry [M]. Englewood Cliffs, N. J.: Prentice-Hall, 1962: 70.

[46]  LEVI H. Elements of algebra [M]. New York: Chelsea Pub. Co., 1954: 13.

[47]  KELLEY J L. Introduction to modern algebra [M]. Princeton, N.J.: Van Nostrand, 1960: 86.

[48]  LAWVERE F W. The language of algebra [M]. Wilmette: Encyclopaedia Britannica Films, 1961: 20.

[49]  BRUMFIEL C F. Algebra I [M]. Mass: Addison-Wesley Pub. Co., 1961: 189.

[50]  EULER L. Introduction to analysis of the infinite [M]. New York: Springer-Verlag, 1988: 3.

[51]  EULER L. Foundations of differential calculus [M]. New York: Springer-Verlag, 2000: vi.

[52]  KLEINER I. Evolution of the function concept: A brief survey [J]. College Mathematics Journal, 1989, 20 (4): 282-300.

[53] RÜTHING D. Some definitions of the concept of function from J. Bernoulli to N. Bourbaki [J]. Mathematical Intelligencer, 1984, 6 (4): 72-77.

[54]  BOURBAKI N. Elements of mathematics: Theory of sets [M]. Paris: Hermann, 1968: 81, 351.

[55]  KARP A, SCHUBRING G. Handbook on the history of mathematics education [M]. New York, NY: Springer, 2014: 257-282, 323-334, 459-472.

[56] 马忠林．数学教育史[M]．南宁：广西教育出版社，2001：340-391．

[57]  HOWSON G. A history of mathematics education in England [M]. Cambridge: Cambridge University Press, 1982: 75-96, 141-168.

[58]  YOUNG J W A. The teaching of mathematics in the elementary and the secondary school [M]. New York: Longmans, Green, and Co., 1907: 308.

[59] HEDRICK E R, National Committee on Mathematical Requirements. The function concept in secondary school mathematics [M]. Washington: Govt. Printing Office, 1921: 1-3.

[60]  HASSLER J O, HEDRICK E R, SMITH R R. The teaching of secondary mathematics [M]. New York: The Macmillan Co., 1930: 231-233.

[61] National Committee on Mathematical Requirements, Mathematical Association of America. The reorganization of mathematics in secondary education [M]. The Mathematical Association of America, inc., 1923: 24-26．

The Concept of Function in Early Algebra Textbooks of the United Kingdom and the United Stated

LIU Si-lu1, SHEN Zhong-yu2, WANG Xiao-qin1

(1. College of Teacher Education, East China Normal University, Shanghai 200062, China;2. School of Mathematical Sciences Soochow University, Jiangsu Suzhou 215006, China)

Focusing on the concept of function, we investigated 216 kinds of American and English algebra textbooks published from 1810 to 1969. We found that according to the time sequence, there are five kinds of definitions of function: “expression”, “variable dependence”, “variable correspondence”, “set correspondence” and “ordered pairs” respectively. The trajectory of its evolution is not only influenced by the historical development of the concept of function itself, but also related to the development of mathematics education. The evolution process and reasons of the concept of function in early textbooks provide important implications for cultivating students’ key competency, understanding students’ cognitive obstacles and improving function classroom teaching.

the concepts of function; early textbooks; definitions; evolution; history of mathematics education

G40-059.3

A

1004-9894（2021）04-0055-08

刘思璐，沈中宇，汪晓勤．英美早期代数教科书中的函数概念[J]．数学教育学报，2021，30（4）：55-62．

2021-04-10

上海高校“立德树人”人文社会科学重点研究基地之数学教育教学研究基地研究项目——数学课程与教学中落实立德树人根本任务的研究（A8）

刘思璐（1995—），女，陕西咸阳人，博士生，主要从事数学史与数学教育研究．

[责任编校：周学智、陈汉君]