基于核心素养的六年级学生数感现状调查研究

孙 虎，张伟平，陈志辉，马艳娇

基于核心素养的六年级学生数感现状调查研究

孙 虎1，张伟平2，陈志辉3，马艳娇1

（1．同济大学附属实验中学，上海 201805；2．上海师范大学数理学院，上海 200234；3．华南师范大学 教育科学学院，广东 广州 510631）

数感是初中阶段的十大关键能力之一，也是核心素养中审辨思维的重要表征形式．研究梳理了数感的内涵以及结构，并指出数感是在一定情境中处理数、数的运算以及数的评估的一种能力．通过对上海地区六年级学生的数感进行研究，发现六年级学生的数感发展水平在性别和成绩方面存在差异，六年级学生的数感发展水平受已有数学认知的影响，同时，六年级学生在评估和情境领域的数感表现受迷思概念的影响．教师在教学过程中要培养学习自信以减少差异，改善数相关知识的教学以及加强数的体验以减少迷思概念的产生．

核心素养；数感；六年级；调查研究

1 问题提出

在《义务教育数学课程标准（2011年版）》（下文简称《课标（2011年版）》）中，数感作为义务教育阶段与符号意识、空间观念等十大需要发展的核心内容之一，有着无可替代的作用．《课标（2011年版）》的总目标指出，要在经历数与代数的抽象过程中建立数感和符号意识．具体来说，要在小学低年级阶段发展数感，在中小衔接阶段初步形成数感，并在中学高年级阶段建立符号意识[1]，同时，这与发展学生学科核心素养中的“知识理解”层面也有着密不可分的联系[2]．可见，对数感的培养是贯穿在整个义务教育阶段的重要内容．

有研究[3]指出，建立数感在提高学生的数学素养、帮助学生自我建构数学知识、发展学生的创新精神和实践能力以及提高文化修养等方面都具有重要的教育价值．而这与《课标（2011年版）》阐述中，将“建立数感”作为数学思考领域的首要目标的理念不谋而合．在国内外，数感的教与学也一直是数学教育研究的重要课题，对数感的概念界定[4-6]、对数感现状的调查[7-10]，对数感的测量[7，11]、对数感培养方式的探索[12]，都有很多学者进行潜心研究．

因为在认识上对数感还存在着诸如简单化、泛化、混淆、借用、甚至神秘化等问题[13]，所以对数学教育工作者、研究人员和课程设计人员来说，评估数感也就成了一项重要而富有挑战性的工作．即便如此，依然有研究者通过自己对数感的认识来设计符合特定阶段测试者的问题进行定性与定量的研究．比如谢茜[14]就对中国五六七年级学生的数感进行测量并对各个年龄段的结果进行比较研究，夏小刚等人[15]通过调查中国七年级的学生的数感并用所得结果进行国际比较，赵倩等人[8]则借助中国台湾研究者开发的数感测量工具对中国大陆和中国台湾小学生的数感进行比较研究，在实践层面做出了卓越的贡献．

通过文献检索发现，虽然国内有很多对数感特征的探讨以及对中小学生数感的调查研究，但是对上海地区学生数感现状的调查研究较少．上海作为PISA等测试的中方代表，其学业成就及关键能力等综合素养也有着突出的表现，作为数学课程核心内容之一的数感的现状也应该在教学与研究过程中被作为重要的参考依据．上海地区的现行学制为“五四学制”，六年级作为初中的起始年级，这一阶段的学生数感现状对中小学的数感培养都具有重要的借鉴意义．因此，研究以上海地区的六年级学生为研究对象，对学生的数感现状进行调查研究，试图管中窥豹，获得这一地域学习群体的数感特征，为教学和研究提供实践依据．

2 概念界定

2.1 数感的内涵

“数感”一词的内涵在教育学界一直难以界定．现行《标准（2011年版）》将数感的概念描述为：“数感主要是指关于数与数量、数量关系、运算结果估计等方面的感悟．建立数感有助于学生理解现实生活中数的意义，理解或表述具体情境中的数量关系．”从中可以看出，前半句话是对数感的描述性叙述，将数感表述为一种“感悟”；后半句话指出随着数感的发展，可以对哪些方面产生影响．显然，这还不足以让人们对“数感是什么？”“数感含有什么？”等问题产生清晰的认识．

很多学者都从不同的角度对数感的内涵撰文进行探讨．比如，史宁中和吕世虎[16]认为数感是对数的感悟，这种感悟既通过肢体又通过大脑，因此同时含有感知和思维这两种成分，这一观点与《课标（2011年版）》类似．叶蓓蓓[17]认为“数感”是一种对数字（量）的直觉，同时还是一种敏捷的感知，这种直觉还可以培养，且具有非逻辑性、非演绎性，反应时间短以及不稳定等特点．同样持有“直觉”观点的还有詹国樑，他认为数感可以从广义与狭义两个角度分为“数字感”和“数学感”，数感是对数、数字或者数学对象的洞察与领悟[18]．马云鹏和史炳星[6]则认为，数感是一种主动地、自觉地或自动化地理解和运用数的“态度”与“意识”，是明确数的概念、进行计算等数学活动的基础．

徐文彬和喻平[13]在对“感悟说”“直觉说”“敏感说”等观念进行评价的基础上，提出：“数感”包括“对数字关系和数字模式的意识”，以及运用这种对数字关系和数字模式的意识“灵活地解决数字问题的能力”两个部分，其核心是指计算策略中的灵活性和创造性，而非“没有思维的”计算程序．从中可以看出他们认为数感除了是对数字关系和模式的一种意识，更是灵活运用策略解决问题，以及评估结果的可靠性与过程的逻辑性的能力，这一能力也正是马利红等人[19]在21世纪核心素养5C模型中审辨思维能力的体现．Mcintosh等人[4]也持有相同的观点，即数感是一种伴有意识的能力，他们认为数感是指一个人对数字以及数字运算的综合理解的能力，倾向于使用这种理解以灵活的方式做出数学判断，同时发展处理数字及数字运算的有效的策略．它反映的是一种使用数字和定量的方法来交流、处理和解释信息的倾向和能力，最终产生一种数字是有用的、数学是有规律的意识．

霍雨佳等人[20]在对数感概念进行梳理的时候发现，现有的对数感定义的取向主要分为行为取向和认知取向，行为论侧重于研究数感表现出的一系列外显行为，认知论注重分析数感的内部心理过程，两种视角分别来自于外显行为和内部心理活动两个层面．从已有对数感的调查研究来看，由于难以在内部心理活动层面进行严谨的调查，大部分研究仍然倾向于从外显行为进行研究，同时有部分研究[8]辅以对被试进行访谈来探索心理层面的因素．

2.2 数感的结构

数感是由多种认知成分所组成的一个整体结构，但是对于具体的内容，已有研究也展示了不同的结构模型．

Mcintosh等人[4]认为数感的结构包含数、运算以及情境等3种基本成分．其中，数包括数的顺序、数的表征以及数的大小3个方面；运算是指在理解运算对数的意义及影响的基础上，对运算结果的合理性进行判断的能力而非常规的纸笔运算；情境是指在理解问题背景中的数量关系的基础上，能够选择有效的方式来表述其中的数量关系，并能够判断问题解决结果的精确性和合理性．

后续的研究者对于数感的分类大多数是建立在Mcintosh等人研究基础上的．比如徐文彬和喻平[13]认为，在解决“需要用数字进行推理的问题”时，关键是要在整合“数字知识和数字的简便性”与“运算知识和运算的简便性”的基础上，形成或获得以下这些理解力、意识和倾向：（1）理解问题情境与合适的解题策略之间的关系；（2）意识到存在多样化的数字呈现方式；（3）应用有效呈现和（或）方法的倾向；（4）检验数据和结果的倾向．Cheung[21]以及Lin[11]等研究团队则在对数感进行测量时将数感分为理解数字和运算的基本含义的能力，识别数字大小的能力，使用数字和运算的多种表征的能力，识别运算对数的相对影响的能力，及判断计算结果合理性的能力等5个方面．

霍雨佳等人[20]则通过对国外已有研究的梳理，依据数感的测评内容，将数感结构分为数、运算、估计以及情境等4种成分，共包括数的意义等10种内容，并将这些内容细分为基数（数量的数）等21个测量指标，并构建了数感三维结构模型．但是引文[22]中提到的“估计”成分是针对幼儿提出的，研究在对数感成分进行梳理时认为，六年级的学生数感应该包含对数和关系两种内容的估计，命名为“评估”更加贴切．据此，研究重新构建了数感的三维结构模型——四面体数感结构模型（如图1）．

图1 四面体数感结构模型

基于以上述论，研究将数感的概念界定为：数感是能够借助对数、数的关系以及数字模式的意识，灵活处理数（包括数的量和序）、数与数之间的关系（包括对数进行运算和比较）以及转换不同情境中数的形式（包括去情境化和带入情境化）的一种能力．主要包含无情境（或基于情境）的数、数的运算以及数的评估等3种成分6个内容．

2.3 数感与核心素养的关系

《课标（2011版）》从数感的界定和作用两个方面描述了数感的表现，指出数感是关于数与数量的感悟、理解现实生活中数的意义、理解或表述数量关系等[1]．数感的研究对象以数与数量、数量关系、运算结果的估计与解释等为主，包含多个层次的具体内容且以客观描述为主．也有研究者从意识与能力的角度出发，认为数感是数的抽象意义与数的具体意义的统一，是一种自觉地基于数或现实的情境，解释和应用数的意识和能力[23]．

就实际表现而言，核心素养是个体面对现实生活情境时，运用已有观念、思维模式和技能进行分析、解释和交流问题的综合品质[24]．数学学科的核心素养是数学育人价值的集中体现，《普通高中数学课程标准（2017年版）》指出，核心素养是学生通过数学学科的学习逐步形成的价值观、必备品格和关键能力[25]，共包含数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析等6个要素．这一描述指出了学生在经历教学过程后应该达到的发展目标，是一种聚焦于人的发展的描述．也有学者从数学素养的内涵出发，认为素养是后天通过短时的培养和练习就能获得的知识、技能、技巧等经验系统，更注重个体在数学活动中的动态生成过程和效果[26]．其本质是描述一个人经过数学教育后应当具有的数学特质[27]．

从以上关于数感和核心素养的表述可以看出，两者都含有主观培养的“观点”“感悟”以及客观形成的“能力”和“品格”等内容，两者也都含有“问题解决”“数学思维”和“数学交流”等核心能力要素[28]．从概念范围看，数感的概念更为具体，内容以数的意义、关系以及运算的结果等为主，更多地是从客观层面描述数学本身的体系．而核心素养以发展要素的形式提出，主要以学生本身的发展目标为主．在实际教学中，让学生感悟、形成和发展数学学科核心素养需要将数学内容与数学学科核心素养进行有机结合[29]，从两者的关系来看，数感的良好发展是形成数学核心素养的前提，数学核心素养也能促进学生数感的发展．同时，数学核心素养的6个要素也为数感指出了发展的方向．

3 研究设计

3.1 研究问题与方法

上海学生在国际数学评估测试中一直表现优异，在2018年的国际学生评估项目（PISA）的测试中，中国的4省市学生均分居79个参测国家（地区）首位，具体到3个测试的领域，数学领域的均分又高于阅读和科学，更是超出第二名新加坡22分之多[30]．而数感作为数学领域的核心内容之一，是发展符号意识、运算推理能力以及应用意识的重要基础，是数学学业的保障，对数学学习有着举足轻重的作用．从刚刚发布不久的《面向未来：21世纪核心素养教育的全球经验》研究报告中也可以看出，核心素养主要由文化理解与传承素养、审辨思维、创新素养、沟通素养以及合作素养等5个部分组成[31]，上海学生在这些维度有怎么样的表现也值得期待．

有研究[32]表明，数感是预测未来数学成绩的精确指标，因为数感与解决数学应用问题的能力密切相关．王本法和乔福强[33]也对数感、数学效能以及学业成就之间的关系进行过研究，发现虽然数感和数学效能均与数学成绩存在显著相关，但是数感与数学成绩的关系较之数学效能与数学成绩的关系更紧密，而且数感对数学成绩的预测力强于数学效能对数学成绩的预测力．基于此，研究主要关注上海地区六年级学生的数感表现，同时从多维度观测数感呈现的特点，并通过学生在数感中的表现，探索在核心素养的培养过程中可以采取的教学策略．聚焦于以下两个问题：（1）上海六年级的学生在数感测试中各个结构的表现分布如何？在数感的迷思概念中呈现出何种特点？（2）该群体学生在数感的测试中对应地在何种程度上表现出了哪些核心素养？在课堂教学中应该如何对这些核心素养进行培养？

研究采用数感双层测试的调查研究法，测试时间为40分钟，强调每道题目的理由部分务必写出自己的思考过程．测试过程中不能交流也不能向教师询问，测试结束后当场收回测试卷．阅卷后，对部分结果选择错误且理由无法理解的学生进行访谈，进一步了解其心理活动层面的活动过程，主要询问：（1）选择某一选项的理由；（2）理由解释的更具体的阐述；（3）对其它没有做出选择的选项的想法．

3.2 测试卷的编制与赋分

根据已有研究，首先将数感分为数、运算、评估以及情境等4个成分，由于绝大多数情境类问题都依托于前3个成分，所以将情境类问题设置在前3个成分中进行测试，同时，所有含有情境类的问题都额外设置一道非情境类问题进行测量用来规避对其它成分的干扰．考虑到4个成分中的具体指标之间存在着相互依存的关系，在设计问卷时仅考查到内容维度．同时参考已有研究[34]，最终测试问卷共包含“数”“运算”“评估”和“情境”等4个维度共16个问题．研究中涉及到的基于情境的数感调查分析数据，分别从测验的前3个维度提取．其中，“数”的维度取1-1到1-6题的测量数据，“运算”的维度取2-1到2-6的测量数据，“评估”的维度取3-1到3-4的测量数据，“情境”的维度取1-3，2-2，2-3，2-5，3-1等5题的测量数据．已有关于数感的研究测试主要以选择和标记题为主要作答形式，采用纸笔或者在线的测试方式．借鉴已有各种研究形式的利弊，研究选取纸笔、全选择题的测量方式．

测试采用两层计分模式，每个问题包含答案选项和理由叙述两个部分，答案选项分值设置为2分，用来检测学生的答题正确情况．选对得2分，选错或者未选得0分．理由叙述的分值设置为4分，主要观测学生在解题时的思维策略．思维策略分为数感思维策略、传统算法策略、迷思概念以及猜测策略等4种情况，根据学生展示的思维策略分别赋予4、3、2、1分．具体评分标准如表1所示．

表1 数感测验评分标准

3.3 研究对象的选取及数据的处理

2020年5月18日下午，选取上海市某公办初级中学六年级的4个班进行施测，各个班级的测试过程和要求保持一致，测试时间40分钟．共发放问卷135份，收回有效问卷131份，其中男生58人，女生73人．有理数的运算内容在小初衔接段内处于重要地位，在培养数感的同时也能够很好地反映数学抽象、逻辑推理、直观想象、数学运算和数学建模等核心素养内容水平[35]．在施测前，他们刚刚学习完“有理数”的相关内容，与小学阶段相比，对数的认识有了进一步的提升．所以，学生的学业水平等级根据他们在测量之前所学的“有理数的运算”中连续两个月的数学成绩均值确定，划分为优秀（≥90分）、良好（≥80分且＜90分）、中等（≥60分且＜80分）和不及格（＜60分）等4个等级．

使用Excel和SPSS 22.0对收集的数据进行描述统计、信度以及方差分析，考查数感问卷中各维度之间的相关性．分析前，对收集到的问卷数据用Cronbach’s系数分析，得出数感量表的信度达到了0.825，表示在可接受的范围内．

利用相关分析来检验数感各分层次之间是否存在相关性，在行为科学领域，通常把相关系数0.3以上视为中等相关，0.5以上视为高相关[36]．如表2所示，组内两两层次在显著性检验水平为0.01时，相关系数在0.436～0.814之间，为中高程度正相关．4个层次与数感总量表之间在显著性检验水平为0.01时的相关系数在0.695～0.910之间，表明各层次与整个问卷具有高度一致性，达到高程度正相关．

表2 各分析层次间的相关系数矩阵

注：**表示在置信度（双测）为0.01时，显著性相关

4 研究结果

4.1 六年级学生的数感发展水平与学生的性别和成绩的相关性

研究结果表明，六年级学生的数感水平（如表3）受到性别和成绩的影响比较明显．从性别角度进行观察，男生在数感的4个维度及总体表现中全面高于女生．为了更详细地分析相关数据，首先从性别角度对单因素方差分析的前提进行检验，经检验，5个维度的相伴概率为0.251～0.966，全部大于显著性水平0.05，可以认为各个组总体方差是相等的，满足方差检验的前提条件．从方差分析结果表（表4）可以看出，方差检验的值为3.314～9.093，相伴概率只有“数”的维度大于显著性水平0.05，表示接受零假设，也就是说不同性别对运算、评估、情境以及数感整体的表现中都有显著的影响．

表3 不同性别及学业水平的学生在数感各维度上的表现

表4 不同性别和成绩对数感影响的方差分析

从表3也可以看出，成绩对数感的表现也有明显的影响，从整体上表现出学业水平越高，数感表现越好的状态．为了进一步研究，先对成绩维度的单因素方差分析的前提进行检验，结果如表4，相伴概率为0.122～0.642，大于显著性水平0.05，满足方差检验的前提条件，从方差分析结果（表4）可以看出，方差检验的值为4.982～13.142，相伴概率全部小于显著性水平0.05，可见不同成绩水平对数感整体及其所包含的各个维度都有显著的影响．

4.2 六年级学生数感发展水平和已有数学认知水平的关系

已有研究[37]表明，学生的数学认知水平和认知方式会影响学生的数学学习，从而影响他们的数学能力水平．从解读问题时对数学概念的理解，到解决问题时对数学技能和数学策略的使用等，都会调动已有的数学认知经历．学生在问题解决过程中使用的数学概念本身也经历着多个不同的阶段[38]，对这些概念的正确理解会在很大程度上影响他们的数感水平．为了探寻数感水平的呈现是否受已有数学认知的影响，选取部分同学对两道有代表性的问题进行访谈．

问题1（数—意义—序数）：你觉得1.52和1.53之间有多少个小数？

A．0个； B．1个； C．几个； D．无数个．

此题在所有测试的小题中均值最高，达到了5.725，表明大多数同学能够借助数感的思维策略获得正确的结果．为了进一步了解学生对此题的想法，选择了几位学生进行访谈，学生A认为“因为这个题目中的小数没有数位的限制，所以我可以不断地从十分位、百分位、千分位……无限写下去”，学生B认为“因为小数的位数可以有无数种可能，所以在这两个数之间的小数也可以有无数个”，学生C则通过举例“大于1.52小于1.53的小数可以是1.521，1.521 1，1.521 11……这样可以无限写下去”．访谈的过程中，他们都提到了他们对这一题的认知来源于前不久学习的“有理数”一章，知道了数轴的相关概念，并且了解了在数轴上表示数的任意两个点之间还有无数个数．

问题2（评估—数量—基准数）：小明使用计算器计算得到算式0.497 5×9 428.8=4 690 828，但是结果忘记了写小数点，不经过精确的计算，请你估计一下下列选项中哪一个是正确的结果？

A．46.908 28； B．469.082 8； C．4 690.828；

D．46 908.28； E．无法确定．

此题在所有测试的小题中均分最低，仅有2.450分．表明大部分学生无法正确借助数感或者传统计算的策略判断结果的正确与否．在选择的几位具有迷思概念的访谈者中，基本上都持有“0.497 5有4位小数，9 428.8有1位小数，相乘以后也会有1+4=5（位）小数，所以运算结果的小数点要向前移动5位”或者类似的观点．通过追问获知，他们从小学阶段学习“小数的乘法”以后就一直持有这一观点．但是，在经过访谈者提示需要考虑两个数相乘末尾是一个或多个0的情况后，他们会立即获得正确的结果．同时，接近0.5的数与9 428.8相乘，乘积的范围应该略小于9 428.8，而在做错此题的学生中，没人能够从两个数的范围角度意识到这一点．

4.3 六年级学生在评估和情境领域数感表现受迷思概念影响

从表4的数据可以看出，评估和情境维度的数感表现明显低于数和运算维度．细化到具体的指标（如表5）．

表5 评估与情境维度各指标统计

可以看出，学生在评估维度的“数量—基准数（2）”和“图形—参考点（1）”的均值只有2.450和2.649，明显低于评估维度的总体均值3.244 3，表现不甚理想．同时，在情境维度的“运算—意义—度量”的均值仅有3.122，在“评估—图形—参考点”的均值仅有2.649，也显著低于情境维度总体均值3.760．这些不佳表现的原因，除了如前述问题2（评估—数量—基准数）中的分析一样，受到已有数学认知水平的影响，还受到迷思概念的影响．

问题3（评估—图形—参考点（1））：如图，小明从点出发，绕着正方形花坛走一圈，请问图中哪个点是小明大约走了2/3的点？

A．点；B．点；C．点；D．点；E．不知道边长，无法确定．

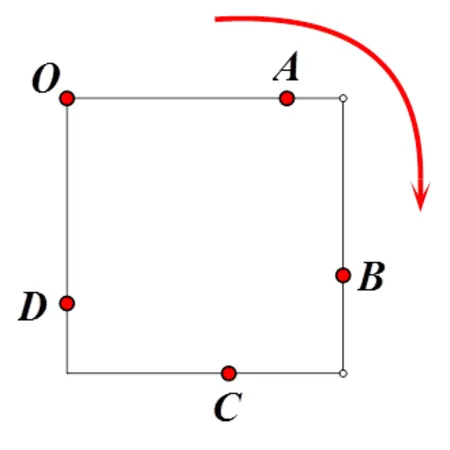
被调查学生在以数轴为基本图形的“数—表征—图形”中的均分为4.550，可见他们在标准几何图形情境中的表现较好．而在问题3中考查学生在折线段中寻找正确参考点的能力时，表现却大相径庭．这种在被赋予实际意义的非标准几何图形情境中的数感能力表现的降低与已有研究[39]不谋而合．比如，有些同学的理由是“切分出来1/3是一条边和半条边，所以选D”，或者“看图可知，D离O点更近，是一大半，2/3也是一大半”等迷思概念，虽然有比较的思想，却缺少对数值精度的考量．

问题4（运算—意义—度量）：下图是两个礼盒，其中甲礼盒是各边长都为10cm的正方体，乙礼盒是高和两个底面直径都为10cm的圆柱体，如果用图示方式进行包装，在不经过精确计算的情况下，请问哪个礼盒需要的丝带更多？

A．甲礼盒用的多；B．乙礼盒用的多；C．两个礼盒一样多；D．无法确定．

被调查学生在问题4中的数感表现也不是很理想，均分只有3.122．主要表现在无法区别所给两个几何物体的异同，从而做出“两个礼盒的边长、高和底都是10 cm，所以所用丝带相同”的错误判断，或者对几何图形本身持有迷思概念，从而有“相同数值长短的图形中，圆的面积最大”“曲线比直线长”等理由的产生．即使选择正确答案A的同学中，也有诸如“甲礼盒表面积更大”“甲礼盒的体积更大”等迷思概念策略的使用．

5 结论与讨论

5.1 性别和成绩差异对数感表现有影响

研究在性别差异方面数感表现的结论与陈京军等人[40]得到的结论类似，初中男生的数学积极情绪多于女生，所以在完成积极情绪体现较多的数学任务的过程中，男生的表现会优于女生．同时，有研究[41]认为，在涉及到与数学能力有关的研究中，中学生虽然表面上不认为女生的数学能力不如男生，但是受到性别刻板印象的影响，内心深处认为女生的数学能力比男生差，随之带来的焦虑感也会影响到她们在相关测验中的表现．也就是说，女生需要在数感培养方面增进自信心．

研究中，数感表现受到成绩差异影响的结论与谢茜[14]的研究成果存在差异．谢茜在研究中分别选取了上海的一所公办中学六年级和民办中学七年级一共88名学生进行测试，认为成绩与数感没有相关性，经初步分析，这一结论与本研究的差异可能是由于被试的学习环境和年级不同而造成．在另一项研究[33]中，研究者认为数感与数学成绩的关系更紧密，同时，数感对数学成绩还有着较强的预测力，认为数感和数学成绩之间确实存在着显著的相关性．可见，成绩与数感的相关性受到多方面因素的影响．

5.2 数感表现受到数学已有认知水平的影响

学生的数学认知水平，特别是对数学概念的理解水平会影响学生数感能力的表现．很多研究都表明，已有数学认知是数学核心素养的重要影响因素．常磊和鲍建生[42]在阐释了数学核心素养与已有数学学习情境之间的关系后指出，数学核心素养是学生在具有情境的数学活动中切实感悟、综合理解、反复强化逐渐形成的．要想发展学生的数感和核心素养，就需要增加与多样化情境相联系的学习体验以优化数学认知．学生从小学的数学课程中，就已经对数学的基本思想有所体会和经历，而这些经历形成的数学认知都影响着学生核心素养的形成[43]．所以有研究者[44]提出，应该从小学开始对学校的课程进行统整和开发以提升学生的数学素养和创新能力．

5.3 迷思概念对数感表现的影响较大

许桂清[45]认为，迷思概念是指学生在学习相关知识的前、中、后3个阶段存在的残缺或者错误的认知，同时认为学生的迷思概念可以从深层思维角度分为“本体论知识”和“经验思维模式”．值得注意的是，迷思概念的产生可能由“本体论知识”或者“经验思维模式”或者两者共同作用导致．比如，问题3中出现的迷思概念可能受到本体论知识“2/3比一半大”的影响，学生只知道大，却无法估算出大的范围．问题4中出现的迷思概念可能是受到经验思维模式“相同长、宽高的物体的表面积相等”的影响，而忽略了形状上面的差异而得到了错误结果．问题4中也存在着有两个因素共同作用的“甲礼盒的表面积（体积）更大”等迷思概念，忽略了丝线是长度单位，而选择了面积和体积单位进行比较．研究认为，要想提高学生在数感方面的表现，就不得不重视对他们在评估和情境领域中迷思概念的改善．

6 教学建议

6.1 教学中丰富学生的数感体验以减少迷思概念的产生

数学体验是由学生经历心智操作和心力操作以后，个体给数学知识赋予意义并认识数学知识的价值的过程，这一经验可以存储于个体的长时记忆系统之中[46]．教师在教学过程中如果能够借助教学活动，构建合适的学习情境，让学生充分实践和感受“测量不同物体的高度”“确定不同规格不同价格的同一种商品的性价比”“将环形操场四等分”等数学活动，便会让学生在潜移默化中增强对一些现实情境中物体的估算能力，而这些都是在数感调查过程中展示出来的薄弱内容．同时，学生在解决可操作的数学活动题时，能够增加对生活中的数学的情感体验，还可以丰富思维过程[47]，并能在对自己的解题思路进行反思和调整的过程中发展数学创造能力．

6.2 优化数感相关知识的教学以提高学生的数感水平

数学抽象、逻辑推理和数学建模是数学学科核心素养3个基本要素，在教学过程中，数的概念、性质、关系和规律是培养学生数感能力的具体表现形式[29]．学生对数的知识的理解对数感水平具有很大的影响，比如在评估维度，对长方体和圆柱体相关概念的理解会在很大程度上影响结果的判断．又如在数的维度，对数位的正确判断会有助于数感水平的提高．对数的关系和规律的认识也会影响到学生对“参考点”的选择[8]．由于在评估和情境部分的数感能力表现与数、计算维度的表现差别主要受到已有数学认知的影响，所以教师在教学过程中除了要注重知识和技能的教学，更应该加强对数学概念、性质、关系和规律等内容的认识，加强上述核心素养表现内容能力的培养．

6.3 培养学生的学习自信以减少性别差异的程度

已有研究[48]表明，在初中起始阶段学生数学学业成绩没有性别差异，但是随着年级的升高，会存在较小程度的性别差异．而且性别差异常表现为女生优于男生[48-49]．这可以归结于女孩更倾向于在学业上付出努力，且对学业拥有更高的兴趣和更好的习惯．但是在遇到具有挑战性的学习内容时，男生更愿意付出精力参与问题的研究[50]．同时，学校教育对女生的消极归因方式以及学习中的心理劣势也是影响女生成绩和能力的因素之一．从研究结果可以看出，女生和学困生在数感的能力水平方面都有待提高．在教学过程中，需要帮助女生以及学困生树立更多的自信．一方面需要避免女生对成绩归因的消极影响，另一方面需要鼓励女生及学困生进行更多的自主性学习活动以消除心理劣势．

7 局限与展望

研究对数感构成要素及主要成分进行了梳理并提供了数感测量的一种方式，对后续的相关研究具有借鉴意义．调查得到的上海地区六年级学生的数感现状，对教学实践的完善也有一定的帮助．由于调查的局限性，实验的样本容量较小，所得到的结论是否具有普遍性还有待进一步验证和研究．同时，数感的构成要素以及数感与数学核心素养的关系仍然需要进一步厘清．数感作为义务教育阶段的核心能力之一，在各个年级与学段中的表现情况、教学过程对数感的影响等都有很高的研究价值．

[1] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：1-15．

[2] 喻平．发展学生学科核心素养的教学目标与策略[J]．课程·教材·教法，2017，37（1）：48-53．

[3] 膝发祥．数感及其教育价值[J]．课程·教材·教法，2004，24（12）：47-50．

[4] MCINTOSH A, REYS B J, REYS R E. A proposed framework for examining basic number sense [J]. For the Learning of Mathematics, 1992, 12 (3): 2-44.

[5] DEHAENE S. Précis of the number sense [J]. Mind & Language. 2001, 16 (1): 16-36.

[6] 马云鹏，史炳星．认识数感与发展数感[J]．数学教育学报，2002，11（2）：46-49．

[7] DER-CHING Y, CHUN-JEN H. Teaching number sense for 6th graders in Taiwan [J]. International Electronic Journal of Mathematics Education, 2009, 4 (7): 92-109.

[8] 赵倩，吕世虎，韩继伟．中国大陆与台湾地区小学生数感表现的比较研究——以比较分数的相对大小为例[J]．数学教育学报，2019，28（6）：65-70．

[9] MERAL C A, EMINE T Ö, HAYAL Y M. Examination of the number sense skills of secondary school students (6th-8th Grades) [J]. Journal of Education and Practice, 2017, 8 (25): 199-207.

[10] GUREFE N, ONCUL C, ES H. Investigation number sense test achievements of middle school students according to different variables [J]. American Journal of Educational Research, 2017, 5 (9): 1 004-1 008.

[11] LIN Y, YANG D, LI M. Diagnosing students’ misconceptions in number sense via a Web-Based Two-Tier Test [J]. Eurasia Journal of Mathematics, Science and Technology Education, 2016, 12 (1): 41-55.

[12] YANG D, LIN Y. Using calculator-assisted instruction to enhance low-achievers in learning number sense: A case study of two fifth Graders in Taiwan [J]. Journal of Education and Learning, 2015, 4 (2): 64-72.

[13] 徐文彬，喻平．“数感”及其形成与发展[J]．数学教育学报，2007，16（2）：8-11.

[14] 谢茜．对我国5、6、7年级学生数感现状的调查研究[D]．上海：华东师范大学，2006：10-63．

[15] 夏小刚，曾小平．七年级学生“数感”的调查与分析——兼谈与国际比较[J]．数学教育学报，2008，17（5）：44-47．

[16] 史宁中，吕世虎．对数感及其教学的思考[J]．数学教育学报，2006，15（2）：9-11．

[17] 叶蓓蓓．对数感的再认识与思考[J]．数学教育学报，2004，13（2）：34-36．

[18] 詹国樑．数感的内涵[J]．苏州教育学院学报，2005（1）：69-71．

[19] 马利红，魏锐，刘坚，等．审辨思维：21世纪核心素养5C模型之二[J]．华东师范大学学报（教育科学版），2020，38（2）：45-56．

[20] 霍雨佳，郭成，杨新荣．国外数感研究评析及启示[J]．课程·教材·教法，2015，35（2）：117-121．

[21] CHEUNG K L, YANG D. Performance of sixth graders in Hong Kong on a number sense three-tier test [J]. Educational Studies, 2020, 46 (1): 39-55.

[22] JORDAN N C, GLUTTING J, DYSON N, et al. Building kindergartners’ number sense: A randomized controlled study [J]. Journal of Educational Psychology, 2012, 104 (3): 647-660.

[23] 曹培英．跨越断层，走出误区：“数学课程标准”核心词的解读与实践研究[M]．上海：上海教育出版社，2017：3-18．

[24] 余文森．核心素养导向的课堂教学[M]．上海：上海教育出版社，2017：29-33．

[25] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2017：4．

[26] 黄友初．我国数学素养研究分析[J]．课程·教材·教法，2015，35（8）：55-59．

[27] 史宁中，林玉慈，陶剑，等．关于高中数学教育中的数学核心素养——史宁中教授访谈之七[J]．课程·教材·教法，2017，37（4）：8-14．

[28] 徐斌艳．数学核心能力研究[M]．上海：华东师范大学出版社，2019：1-13．

[29] 娜仁格日乐，史宁中．数学学科核心素养与初中数学内容之间的关系[J]．东北师大学报（哲学社会科学版），2019（6）：118-124．

[30] 赵茜，张佳慧，常颖昊．“国际学生评估项目2018”的结果审视与政策含义[J]．教育研究，2019，40（12）：26-35．

[31] 魏锐，刘坚，白新文，等．“21世纪核心素养5C模型”研究设计[J]．华东师范大学学报（教育科学版），2020，38（2）：20-28．

[32] JORDAN N C, GLUTTING J, RAMINENI C. The importance of number sense to mathematics achievement in first and third grades [J]. Learning and Individual Differences, 2010, 20 (2): 82-88.

[33] 王本法，乔福强．数感、数学效能感与数学成绩的关系研究[J]．中国特殊教育，2012（6）：87-91．

[34] 许清阳．小学生数感理论模式建构与电脑化数感诊断测验系统之研究[D]．高雄：高雄师范大学，2006：1-286．

[35] 吴增生．数学学科核心素养导向下的有理数教学实证研究[J]．数学教育学报，2020，29（2）：53-57．

[36] 何小亚，李耀光，张敏．数学教育研究与测量[M]．北京：科学出版社，2017：419-436．

[37] 杨红，王芳，周加仙，等．数学学习的认知与脑机制研究成果对数学教育的启示[J]．教育发展研究，2014，33（22）：37-43．

[38] 鲍建生，周超．数学学习的心理基础与过程[M]．上海：上海教育出版社，2009：107-146．

[39] 陈志辉，孙虎，周芳芳．上海七年级学生“平行”概念表征与转译的调查研究——基于数学核心素养的视角[J]．数学教育学报，2019，28（1）：37-42．

[40] 陈京军，吴鹏，刘华山．初中生数学成绩、数学学业能力自我概念与数学学业情绪的关系[J]．心理科学，2014，37（2）：368-372．

[41] 宋淑娟．中学生数学—性别刻板印象威胁与消解[J]．中国教育学刊，2015（1）：88-92．

[42] 常磊，鲍建生．情境视角下的数学核心素养[J]．数学教育学报，2017，26（2）：24-28．

[43] 曹培英．从学科核心素养与学科育人价值看数学基本思想[J]．课程·教材·教法，2015，35（9）：40-43．

[44] 汤卫红，姜国明．整合数学：改变学生的学习样态[J]．人民教育，2015（13）：30-32．

[45] 许桂清．学生迷思概念与科学概念比对图模型的建构与应用[J]．课程·教材·教法，2016，36（6）：97-102．

[46] 赵思林．数学活动经验的含义新探[J]．数学教育学报，2019，28（2）：75-80．

[47] 邢佳立，张侨平．通过数学活动题培养学生创造力的实践探索[J]．课程·教材·教法，2020，40（3）：43-49．

[48] 李美娟，郝懿，王家祺．义务教育阶段学生学业成绩性别差异的元分析——基于大规模学业质量监测数据的实证研究[J]．教育科学研究，2019（11）：34-42．

[49] 郝连明，綦春霞．基于初中数学学业成绩的男性更大变异假设研究[J]．数学教育学报，2016，25（6）：38-41．

[50] 朱雁，倪葎，倪明．初中数学学习难点的性别差异分析[J]．全球教育展望，2019，48（11）：106-115．

An Investigation of the Sixth-Grade Students’ Number Sense Based on Core Competencies

SUN Hu1, ZHANG Wei-ping2, CHEN Zhi-hui3, MA Yan-jiao1

(1. Experimental High School Affiliated to Tongji University, Shanghai 201805, China;2. Mathematics & Science College, Shanghai Normal University, Shanghai 200234, China;3. School of Educational Science, South China Normal University, Guangdong Guangzhou 510631, China)

Number sense is one of the ten core competencies in junior high school as well as a representation form of critical thinking in core literacy. Prior research has sorted out the connotation and structure of number sense and pointed out that number sense refers to an ability to handle numbers, number operations, and number evaluation in certain situations. Through research on the number sense of sixth-grade students in Shanghai, it was found that there are differences in the number sense development levels of the sixth-grade students in terms of gender and performance. The level of the number sense development of the sixth-grade students was affected by existing mathematical cognition. The sixth-grade students’ number sense performance in evaluation and situational domains was influenced by misconceptions. In the teaching process, teachers should improve the teaching of mathematics-related knowledge and strengthen the experience of mathematics to cultivate self-confidence in learning to reduce differences and misconceptions.

core competencies; number sense; sixth grade; investigation

G623.5

A

1004–9894（2021）04–0041–07

孙虎，张伟平，陈志辉，等．基于核心素养的六年级学生数感现状调查研究[J]．数学教育学报，2021，30（4）：41-47．

2021–04–09

上海市中小学（幼儿园）青年教师专业发展实践研究项目——基于循证的职初教师单元设计能力发展的实证研究（QN201903075）；中国博士后科学基金第65批面上资助项目——面向素养培育的初中数学课堂教学评价模型实证研究（2019M652944）；2020年上海市数学高峰项目&上海师范大学校级项目——数学教学中嵌入式培养计算思维研究：教师专业发展的视角&美国注重工科设计的STEM教育和学生生成性工科设计素养培养研究（KF202011）；上海市级项目——基于构造式实践取向的优秀教师课堂关键事件研究（C160060）

孙虎（1988—），男，江苏淮安人，中学一级教师，硕士，主要从事数学教育研究．张伟平为本文通讯作者．

[责任编校：陈隽、陈汉君]