情境在现实问题解决中的作用——基于5套人教版初中数学教科书的纵向比较

李 健，李海东

情境在现实问题解决中的作用——基于5套人教版初中数学教科书的纵向比较

李 健1，李海东2

（1．人民教育出版社 博士后科研工作站，北京 100081；2．人民教育出版社 课程教材研究所，北京 100081）

数学教科书中情境在现实问题解决中的作用，影响着学生问题解决能力的发展机会，对于学生数学核心素养的发展十分重要．通过修订的数学教科书情境作用分析框架，以改革开放40年来不同时期的5套人教版初中数学教科书为分析对象，对其中的现实问题情境编码分析．研究结果显示：5套教科书整体表现出的高水平情境比例偏低，但高水平情境比例上升的发展势头良好．建议未来的教科书建设应注意如下3点：（1）方向性：问题解决能力提升应指向不良结构情境问题的适度增加；（2）科学性：问题情境设置需注重学科特点与学生认知的有效统整；（3）保障性：各水平情境比例调整需关联课堂情境教学的实施反馈．

数学；教科书；教材；情境；问题解决；改革开放；课程改革

1 问题提出

发展学生的数学核心素养，其重要目的在于教会学生如何应用数学解决现实世界中的问题．从学生数学学习的本质看，学生数学学习中的建构过程，始终与知识赖以产生意义的背景及环境相关联[1]，而恰当地设计现实情境问题，将有助学生学会何时、何地和为什么使用他们所学过的知识[2]．由此可见，现实问题情境对学生数学核心素养的培养作用显著．数学教科书作为数学课程的重要显性形态，是数学课程实施的直接载体，也是数学核心素养培养的主要媒介．有研究者指出，随着教科书编写理念由学科知识转向核心素养，教科书内容的情境性成为核心素养取向教科书的基本特征[3]．2018年8月，国家教材局发布《中小学国家课程教材审定·审查细则》，明确指出教科书编写应，“创设切合教学目标的学习情境，……，培养学生解决真实情境中复杂问题的能力”．综上，高质量地设置数学教科书中的现实问题情境，对于发展学生的数学核心素养极为必要，亦为应对中国基础教育课程改革所面临的“培养什么样的人”“怎样培养人”的挑战提供了有力抓手．

近年来，大量学者开始关注数学教科书中“现实世界问题（real world problem）的情境”（简称现实问题情境），如现实问题情境与学生生活的远近程度[4]、“成人化”倾向[5]、“城市化”倾向[6-7]等．从学生数学核心素养发展的角度而言，现实问题情境在问题解决中的作用（简称：情境作用）也受到众多研究者的重视，国外研究者亦称之为情境角色（role of context）[8]、情境使用（context use）[9]．目前，大量研究指出中国数学教科书中存在情境的数学味道不浓[10]、情境呈现的必要性不佳[11-13]等问题，这类问题皆可归因于现实问题情境在问题解决中的作用低下．然而，目前中国对这方面问题的研究，主要集中于研究者对教科书文本的主观认识，抑或源自对一线教师的调查，其结论的客观性与可重复性尚有提升空间，难以为中国数学教科书的理论发展与修订提供定量化的实证支撑．

基于以上分析，首先确定了第一个研究问题：如何刻画情境在现实问题解决中的作用？其次，在第一个问题研究成果的基础上进行应用研究．鉴于改革开放以来，中国数学教育取得了长足进步，考虑从情境作用这一视角对中国数学教科书的发展态势进行梳理，故提出第二个研究问题：改革开放40年来，中国不同时期教科书中情境在现实问题解决中的作用是否发生了变化？如果发生了，发生了怎样的变化？

2 理论框架

对于数学中的“现实问题”，其相同或相近意义的中文表示包括情境问题、应用题等，英文表示包括world problem、application problem、contextualised problem等．现实问题情境是指需要被数学化的数学问题所包含的以及围绕着的信息[9]．为了方便理解，不妨看如下一例：“屋内有3只白猫，4只黑狗和5个黄板凳，问共有多少只宠物？”在这个现实问题中，“3只白猫”“4只黑狗”“5个黄板凳”所涉及的颜色、种类皆属于问题所包含的信息，而由此延展出的“猫叫声”“狗吠声”“板凳作用”等相关信息，属于围绕着问题的相关信息，这些信息都属于问题情境．

已有关于测试题或教科书在内的研究中，关于情境在现实问题解决中的作用的分析，可分为两类．第一类研究关注情境的使用主体，但在评价情境时需要过多地依靠研究者的主观判断，相关研究包括情境的可接受性（accessibility）[14]、聚焦度（focus）[15]等．这类研究容易受研究者的主观认识影响，暂时缺乏有效的量化处理，其研究结论的可重复性与可推广性都有待提升．第二类则偏重问题情境的客观存在，以“问题解决的过程”为分析途径，能够定量化地研究情境在解题过程中的作用．目前而言，第二类的研究过程的可重复性更好，不同研究的结果之间更具可比性．因此，这里选取第二类研究范式，基于问题解决的过程，研究情境在问题解决中的作用．

2.1 情境在现实问题解决中的双重作用

De Lange按照情境在测试题中作用的大小，将问题情境分为3类：无作用情境（no function）、“装饰”类情境（dressed up）、必要且相关类情境（essential and relevant）[16]．并且这种分类方式也获得PISA2003数学专家组（mathematics expert group for PISA2003）的认可[17]．这些研究将现实问题情境在问题解题中的作用进行单一向度划分，为这一领域问题的破局迈出了坚实一步．

但以上单一向度的划分方式，均将问题解决视作整体过程进行思考，忽略了问题解决的阶段性．PISA提出的“数学建模环”将整个数学建模过程分为4个步骤（见图1）：步骤一，将“现实情境问题”表达（formulate）为“数学问题”，这一过程是现实世界向数学世界的转化，即问题的数学化；步骤二，在数学世界中应用（employ）模型求解问题，得到对应的数学结果；步骤三，将数学结果翻译（interpret）为符合情境的结果，这一过程是数学世界向现实世界的转化；步骤四，评价（evolute）所得结果能否充分回答现实问题[18]．

由图1可知，情境在数学建模中的作用，主要体现在与现实世界相关联的“表达”“翻译”“评价”3个过程中．又由于考试测评中，无法提供额外资源让学生评价所得答案在现实情境中的适用性，因此PISA在评价学生的数学素养时，并不报告“评价”这一步骤．综上所述，情境在现实问题解决中的双重作用，具体表现在“数学问题的表达”与“数学答案的翻译”两个过程中．

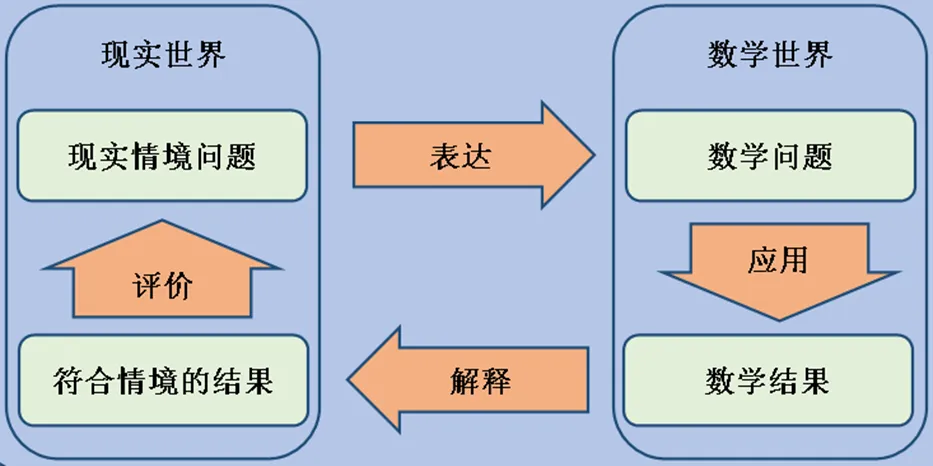
图1 数学建模环

2.2 情境作用分析框架

Almuna Salgado以“表达”与“翻译”为分类依据，构建了“数学问题中情境使用的分类水平理论框架”（theoretical framework for classifying levels of context use for mathematic problem），将问题情境的作用分为两个评价维度：“数学问题的表达”和“数学结果的翻译”，并将每个评价维度划分为三级水平[9]．然而，该框架对两个维度中的第一、二级水平的判定仍缺乏清晰的操作性定义．研究者结合情境的数学关联性层级[17]，对Almuna Salgado的评价框架进行了修订，最终得到“现实问题解决中情境作用的二维分析框架”（见表1）．进行操作性定义时，将是否需要基于现实问题情境补充必要解题条件、是否需要将开放的现实情境问题转化为具体数学问题，作为中水平与高水平“表达”作用的划分依据；将是否需要根据情境说明、判断答案，作为中水平与高水平“翻译”作用的划分依据．

表1 现实问题解决中情境作用的二维分析框架

情境作用的两个维度各具三级水平，两两结合后将形成9种作用情况：A0B0、A0B1、A0B2、A1B0、A1B1、A1B2、A2B0、A2B1、A2B2．进一步，研究综合考虑情境在“表达”与“翻译”上的作用情况，将9种作用情况分为3类（见图2）：第一类，在“表达”和“翻译”上至少有一个处于低水平，将此时情境对问题解决的综合作用定义为低水平（C0）；第二类，在两个维度上同时达到中水平，将此时情境对问题解决的综合作用定义为中水平（C1）；第三类，在两个维度上至少有一个达到高水平且均无低水平，将此时情境对问题解决的综合作用定义为高水平（C2）．以此构建出情境在问题解决中的综合作用水平分析框架，各水平具体说明见表2．

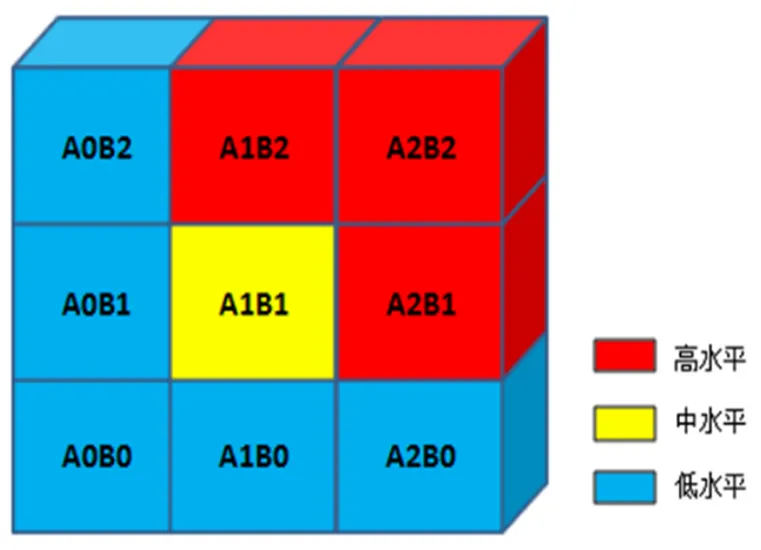
图2 情境综合作用水平的分类

表2 情境在问题解决中的综合作用水平分析框架

2.3 框架应用举例

为了对“现实问题解决中情境作用的二维分析框架”以及“情境在问题解决中的综合作用水平分析框架”进行进一步解释，以下选取不同版本数学教科书中的4道现实情境问题进行编码举例（各版本具体说明见后文），并详细说明编码缘由．

例1 中国古代科学家祖冲之（公元429—500年），算得圆周率π的近似值在3.141 592 6与3.141 592 7之间．这两数相差多少？（78版第一册66页复习题34（2）题）

问题直接表明求3.141 592 6与3.141 592 7两数之差，可以忽略祖冲之以及圆周率这一情境直接展开计算求解，故“表达”水平为A0；所得两数之差即为问题之解，无需返回现实世界，故“翻译”水平为B0．由图2可知，这一情境（A0B0）在问题解决中的综合作用记为低水平（C0）．

例2 某水利工地派48人去挖土和运土．如果每人每天平均挖土5方或运土3方，那么应怎样分配挖土和运土的人数，正好能够使挖出的土及时运走？（83版代数第二册24页例1）

本文应用Graham法和公式（4）分别估算该工况下溃坝造成的生命损失（LOL），估算结果见表6所示。当警报时间小于或等于5 h，生命社会风险均是不可容忍的，采用本文方法计算，当警报时间小于或等于0.5 h，生命社会风险均是不可容忍的，当警报时间大于0.5 h，社会风险是可容忍的，根据工程及城市所在位置来说，本文公式（4）的计算结果比采用Graham法计算结果较符合客观实际。

解决该题时，仅需根据情境提供的信息找到挖土与运土人数间的关系、挖土量与运土量间的关系，便能实现问题的数学化，故“表达”水平为A1；得到数学结果后，需将其转化为现实世界中的人数，故“翻译”水平为B1．由于A1B1属于图2中的黄色区域，故将情境在问题解决中的综合作用记为中水平（C1）．

例3 中国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何？”（13版七年级下册90页习题第4题）

该题为解二元一次方程的实际问题，仅根据题目中出现的信息并不能将问题数学化，还需要学生根据生活经验补充必要解题条件（每只鸡和兔子的头数与脚数），故“表达”水平为A2；得到数学结果后，仅需简单地转化为具体的鸡与兔的数量，故“翻译”水平为B1．由图2可知，这一情境（A2B1）在问题解决中的综合作用记为高水平（C2）．

例4 统计全班同学上学所用时间，对所得数据进行整理、描述和分析，看看你能得出哪些结论．（08版八年级下册154页复习第8题）

该题是一道需要学生收集数据的开放式问题，不仅需要学习者亲自统计全班学生的上学时间，并且需要基于上学时间的分布情况自行确立研究问题，故“表达”水平为A2；而通过数据分析所得到的结论，需要结合班级情况进行具有现实意义的阐明解释，故“翻译”水平为B2．由图2可知，这一情境（A2B2）在问题解决中的综合作用记为高水平（C2）．

3 不同时期教科书中情境作用的演变

人教版初中数学教科书是中国发行量最大、使用范围最广、影响力最大的初中数学教科书，在中国数学课程实施的过程中扮演着重要角色．研究选取改革开放40年来人民教育出版社编写的5套初中数学教科书为分析文本．由于每套教科书中各册出版时间不一，故以最早出版册时间对该套教科书进行命名，分别记为1978版、1983版（包含《几何》与《代数》）、1992版（包含《几何》与《代数》）、2008版、2013版．以上5套教科书分别依据《全日制十年制学校中学数学教学大纲（试行草案）》（1978年）、《全日制六年制重点中学数学教学大纲（征求意见稿）》（1982年）、《全日制中学数学教学大纲》（1987年）、《义务教育数学课程标准（实验稿）》（2001年）、《义务教育数学课程标准（2011年版）》（2011年）进行编写，表明所选取的5版教科书能够代表中国不同时期数学课程的发展特点．

选取教科书中的问题解决类现实情境问题为研究对象，即不包括问题提出类、简单转换类（如用科学计数法表示数）、特点观察类（如图像是否相似）、操作类（如制作笔筒）、作图类（如画三视图）、简单判断类（如判断随机事件）情境问题．经过遴选，最终确定3 209道现实情境问题为分析对象．选取不同编码者，依据表1对每道问题的情境作用进行两次编码，表达、翻译两类作用的总体编码一致性分别为88.3%、89.1%，编码一致性良好（见表3），而对于不一致的编码，共同协商处理．

表3 编码一致性

3.1 情境“表达”作用的演变

表4为5版教科书中不同“表达”水平的情境数量与百分比分布．从1978版到2008版教科书中情境的“表达”作用整体趋势来看，低水平情境的比例逐渐降低，中水平情境的比例逐渐升高，表明在这一阶段，教科书编写者注意到了与问题数学化不相关的情境所占比例过大，开始减少与问题数学化无关的情境．但在2013版教科书中并未遵循这一趋势继续发展，低水平情境的比例略有提升，中水平情境略有下降．

至于高水平问题情境的比例，5版本教科书对这类情境的设置情况都不理想，平均百分比仅为1.8%．但在整体情况不理想的背景下，也能发现一些可喜之处．在1978版、1983版和1992版教科书中，高水平问题情境至多出现2次，而2008版教科书中出现24次，再至2013版出现28次．不难发现，2001年课程改革以后，教科书编写者开始重视高水平“表达”作用情境的设置．

表4 5版教科书中不同“表达”水平的情境数量与百分比

3.2 情境“翻译”作用的演变

表5为5版教科书中不同“翻译”水平的情境数量与百分比分布．从1983版到2013版教科书中情境的“翻译”作用来看，低水平情境的演变呈现出递增趋势．而中水平情境的发展趋势，主要体现在1992版到2013版的比例变化上，在此期间中水平情境的比例逐年下降．

高水平情境的比例从1978版与1983版的12.6%左右，减至1992版的7.9%，再升至2008版与2013版的15.6%左右，整体呈现出“V形”发展趋势．此外，对比2001年课改前的1992版教科书与课改后的2008版教科书：在高水平情境的数量上，后者超过前者的3倍；在高水平情境的比例上，后者超过前者的两倍．以上数据无不说明2001年课改后，教科书编写者对于高水平“翻译”作用的问题情境的重视．

表5 5版教科书中不同“翻译”水平的情境数量与百分比

3.3 情境综合作用的演变

根据“情境在问题解决中的综合作用水平分析框架”，可以得到5版教科书中不同综合作用水平的情境数量与百分比分布，见表6．从1978版到2008版教科书，其低水平情境的百分比逐年下降，但这一比例在2013版教科书中略微上升，5版教科书中除2008版为14.2%，其余4版的整体比例维持在两成左右．而纵览1978版到2013版教科书，中水平情境呈现出先升后降的“A形”发展趋势．至于高水平情境在各版教科书中的所占比例，其整体发展呈现出3个阶段：第一阶段，从1978版的11.6%小幅上升至1983版的13.3%；第二阶段，比例大幅下降至1992版的8.3%；第三阶段，比例翻番，骤升至2008版的17.7%，2013版中这一比例略微下降至16.4%，3个阶段的高水平情境比例呈“V形”发展趋势．

综合考虑5版教科书中不同水平情境的数量与百分比分布，发现1992版与2008版教科书中情境作用的变化较大．从1978年改革开放至20世纪90年代初期，中国数学课程在继承已有经验的同时逐步摸索前进．随着21世纪的来临，国家对于数学教育的要求也有了新的变化，数学课程期待着更能发展学生能力与素养的变革．国家对于数学课程的新要求，在2001年课改后的教科书中得到体现，如2008版与2013版教科书中的“探究”“课题学习”“数学活动”等栏目的增设，都将现实任务与数学学习紧密联系，保证了高水平综合作用问题情境比例的上升．

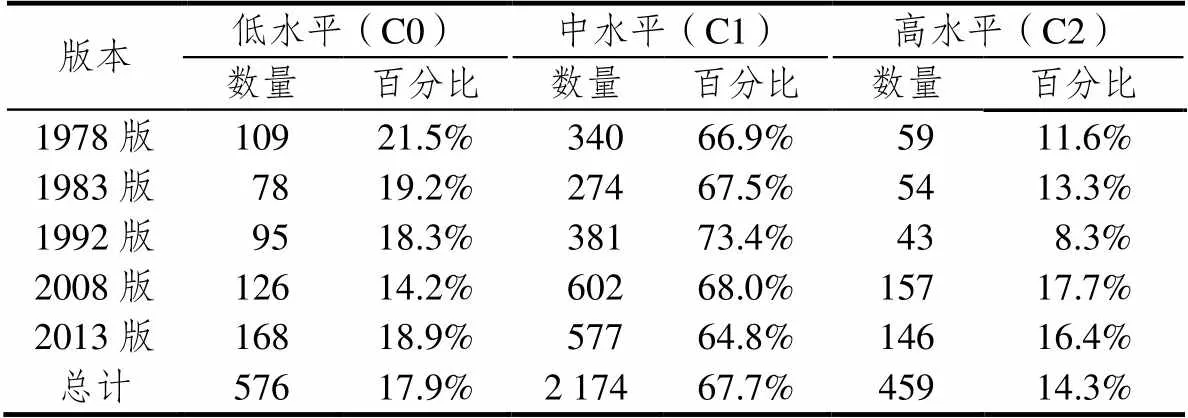
表6 5版教科书中不同综合作用水平的情境数量与百分比

4 讨论与结论

4.1 讨论

进入21世纪以来，中国学生在TIMSS、PISA等国际大型数学测评中名列前茅，但解决现实情境问题的能力却仍有提升空间．如在PISA2012测评中，中国（以上海为代表）、新加坡、韩国、日本等东亚国家的数学成就领先于世界其他国家，但中国学生在问题解决方面的表现却落后于其他东亚国家学生，比其他东亚国家最少低12分[19]．因此，破解中国学生数学学业成就与实际问题解决能力间的不匹配问题，业已成为中国数学课程有效性发展的重要关注点．而导致中国学生“数学学业成就与实际问题解决能力不匹配”的原因复杂多样，研究显示教科书中高水平现实问题情境的匮乏，或许是造成这一现象的可能影响因素之一．

2001年课程改革以来，初中数学教科书中的现实问题情境，在“表达”与“翻译”两个维度上的作用均有所提升．整体呈增长趋势的高水平现实问题情境，体现出中国数学课程对于问题情境的重视，这与20世纪末世界范围内多国所倡导的情境化课程设计理念[1]相一致．这一变革对中国学生现实问题解决能力、建模能力的提升均十分有益，也是对21世纪中国数学课程“应该培养什么样的人、怎样培养人”的有力回应．

4.2 结论

利用修订后的具有可操作性的情境作用分析框架，通过对不同时期初中数学教科书的分析发现：改革开放以来，中国数学教科书中高水平作用情境比例偏低；但2001年课改之后，初中数学教科书中的高水平作用情境明显增加，展现出良好的发展态势．

5 建议

如何处理数学教科书中情境的解题作用？这是情境化理念落地课堂、生根教学的重要着力点，更是教科书研究与建设的深水区．因此提出中国初中数学教科书情境设置的3条建议，分别指向教科书编写的方向性、科学性和保障性．

5.1 方向性：问题解决能力提升应指向不良结构情境问题的适度增加

随着中国数学课程标准对初中生数学问题解决能力要求的不断提升[20]，加强问题解决过程中对情境与问题间的关联度，尤为重要．研究显示，具有不良结构的开放性情境问题更易体现情境在问题解决中的作用．为此，建议适度增加教科书中不良结构问题，注重条件冗余或条件缺失问题的数量提升，这将保证教科书情境作用整体水平的由低至高涌动．适度增加的高水平情境，将保证学生获得更多高质量数学思维锻炼的机会，这是中国教科书指向初中生问题解决能力提升的必由之路．

5.2 科学性：问题情境设置需注重学科特点与学生认知的有效统整

数学教科书是数学课程有效实施的重要教学资源，编写教科书要兼顾数学的学科特点与学生数学学习的心理认知发展特点．不同数学领域之间、不同年级之间，都应纳入情境设置影响因素的范围之内．如代数类问题与几何类问题相比，前者就更容易考察数学模型的建立与现实问题的解决，对高水平问题情境在两类知识领域上设置比例差异的解读，就应该考虑这一因素．只有同时兼顾学科特点与学生认知[21-24]，才能科学把控数学教科书中情境作用的设置．

5.3 保障性：各水平情境比例调整需关联课堂情境教学的实施反馈

数学教科书中不同作用水平现实问题情境的调整，离不开课堂情境教学的实施反馈，以此方可科学配比各水平作用的问题情境．尽管研究者对5版教科书中情境作用的演变进行了量化分析，但其功能仅在于描述教科书的实然状态，未来教科书中各水平情境应该如何调整，亟待一定范围、规模下的课堂反馈支持．合理有效地调查实验区（校）教师的问题情境使用情况，确保收集到真实有效的教科书情境使用反馈，将成为教科书情境作用质量提升的有力保障．

[1] 黄翔，李开慧．关于数学课程的情境化设计[J]．课程·教材·教法，2006，26（9）：39-43．

[2] 约翰·D·布兰思福特．人是如何学习的[M]．程可拉，孙亚玲，王旭卿，译．上海：华东师范大学出版社，2002：44．

[3] 彭寿清，张增田．从学科知识到核心素养：教科书编写理念的时代转换[J]．教育研究，2016，37（12）：106-111．

[4] 王建磐，鲍建生．高中数学教材中例题的综合难度的国际比较[J]．全球教育展望，2014，43（8）：101-110．

[5] 孔凡哲．数学课程标准实验教科书发展中的问题及其对策[J]．教育科学研究，2005（3）：53-56．

[6] 陈志辉．中美两国初中数学课程的问题情境水平比较研究——以“函数”内容为例[J]．数学教育学报，2016，25（1）：5-9．

[7] 章建跃．高中数学教材落实核心素养的几点思考[J]．课程·教材·教法，2016，36（7）：44-49．

[8] van den Heuvel-Panhuizen M H A M. The role of contexts in assessment problems in mathematics [J]. For the Learning of Mathematics, 2005, 25 (2): 2-9.

[9] ALMUNA SALGADO F. Developing a theoretical framework for classifying levels of context use for mathematical problems [C] // WHITE B, CHINNAPPAN M, TRENHOLM S. Opening up mathematics education research (Proceedings of the 39th annual conference of the Mathematics Education Research Group of Australasia), 2016: 110-117.

[10] 董玲．小学低年级数学教科书中的情境题材研究[D]．长春：东北师范大学，2010：34-36．

[11] 曹新，纪雪颖，张永雪．对数学情境及其性质、作用的探讨[J]．课程·教材·教法，2011，31（1）：89-94．

[12] 陈小娴．苏科版初中数学教材问题情境设置现状的调查研究[D]．南京：南京师范大学，2015：39-40．

[13] 赵颖．对北师大版七年级（上）数学教材中问题情境的调查分析及研究[D]．西安：陕西师范大学，2013：38．

[14] LITTLE C T. The use of real-world contextual framing in UK university entrance level mathematics examinations [D]. Southampton: University of Southampton, 2010: 79-80.

[15] AHMED A, POLLITT A. Improving the quality of contextualized questions: An experimental investigation of focus [J]. Assessment in Education Principles Policy & Practice, 2007, 14 (2): 201-232.

[16] De LANGE J. Assessment: No change without problems [M] // THOMAS A R. Reform in school mathematics and authentic assessment. New York: State Universtity of New York Press, 1995: 87-172.

[17] WATANABE R, ISCHINGER B. Learning mathematics for life: A perspective from PISA [M]. Organisation for Economic Co-operation and Development, 2009: 30-31.

[18] 凯·斯泰西，罗斯·特纳．数学素养的测评——走进PISA测试[M]．雷一鸣，译．北京：教育科学出版社，2007：28．

[19] 曹一鸣，梁贯成．21世纪的中国数学教育[M]．北京：人民教育出版社，2018：8．

[20] 高翔．20世纪以来中国初中数学课程标准中数学问题解决能力内涵与要求的演变[J]．数学教育学报，2019，28（3）：30-35．

[21] 史宁中．高中数学课程标准修订中的关键问题[J]．数学教育学报，2018，27（1）：8-10．

[22] 李海东．基于核心素养的“立体几何初步”教材设计与教学思考[J]．数学教育学报，2019，28（1）：8-11．

[23] 李健．初中数学教科书中现实问题情境设置的实证研究——基于中外九版初中数学教科书的纵向与横向比较[D]．天津：天津师范大学，2019：182．

[24] 李健，李海东．数学教科书中设置问题情境的作用与原则[J]．基础教育课程，2020（17）：59-66．

The Role of Context in the Solving of Real-World Problems——A Historical Comparison of Five Editions of PEP Junior High School Mathematics Textbooks

LI Jian1, LI Hai-dong2

(1. Postdoctoral Research Station, People’s Education Press, Beijing 100081, China;2. Curriculum and Teaching Materials Research Institute, People’s Education Press, Beijing 100081, China)

The role of context in solving real-world problems in mathematics textbooks affects development opportunities for students’ problem-solving ability, which is very important for the development of students’ core mathematics literacy. Using the updated analysis framework of the role of context for mathematics textbooks, this paper takes five editions of junior higher school mathematics textbooks published by People’s Education Press in different periods during the 40 years of reform and opening up as the objects of analysis for codes of context. The results showed that the proportion of high-level contexts is relatively low but the proportion is rising over the 40 years. It is suggested that the following three points should be paid attention to in future textbook construction: (1) Directivity: The improvement of problem-solving ability should point to moderate increases in ill-structured problem context; (2) Scientificity: The setting of the problem context should take into account the effective integration of characteristics of the mathematics as the subject and students’ cognition; and (3) Supportability: The adjustment of the proportion of each level of contexts needs to be related to feedback from classroom teaching.

mathematics; textbooks; teaching material; context; problem solving; reform and opening up; curriculum reform

2021-04-28

天津市教育科学“十三五”规划课题——天津市义务教育阶段学生数学学习质量评价研究（BE3282）；人民教育出版社课程教材研究所“十三五”课题——数学教材中问题情境呈现的内容与方法（KC2019-055）

李健（1988—），男，重庆人，博士后，主要从事数学课程与教学论研究．王光明为本文

．

G623.5

A

1004-9894（2021）04-0030-05

李健，李海东，王光明．情境在现实问题解决中的作用——基于5套人教版初中数学教科书的纵向比较[J]．数学教育学报，2021，30（4）：30-34．

[责任编校：周学智、张楠]