高中数学学科核心素养：生成机制与培养路径

武丽莎，朱立明

高中数学学科核心素养：生成机制与培养路径

武丽莎1，朱立明2

（1．唐山师范学院 数学与计算科学学院，河北 唐山 063000；2．唐山师范学院 教育学院，河北 唐山 063000）

基于测量的视角，数学知识、问题解决与数学思维可以构成数学学科核心素养，其结构的基本特征表现为内容构成具有复杂性，发展水平具有双重性，生成路径具有多元性．数学学科核心素养形成于数学学习与应用的过程，“融合—进阶”是数学学科核心素养的生成机制，在培养学生数学学科核心素养时，应以“大概念”为生长点，构建学生学科知识结构；以“真情境”为出发点，培养学生问题解决能力；以“双向度”为切入点，提升学生学科思维品质．

数学学科核心素养；生成机制；培养路径

2018年1月，教育部颁布了《普通高中数学课程标准（2017年版）》（以下简称《课程标准（2017年版）》），凝练了数学学科核心素养，学生数学学科核心素养是核心素养在数学学科的投射，也是核心素养体系学科化的具象表现，在学生数学学习与应用过程中发展形成，数学学科核心素养已经成为不断深化基础教育数学课课程改革的育人理念和引领方向．数学学科核心素养作为对数学课程三维目标体系的继承与超越，具有一定的独特性，为了保证数学课程改革有效实施，促进数学学科核心素养从顶层理念走向实践场域，必须解决两个基本问题，即学生数学学科核心素养的生成机制是什么？学生数学学科核心素养的培养路径有哪些？这里在阐释数学学科核心素养基本结构的基础上对上述两个问题进行探讨．

1 数学学科核心素养的基本结构

1.1 数学学科核心素养结构模型述评

随着数学学科核心素养相关研究的不断深入，关于其结构模型的探究也越来越多，可以概括为以下4类核心观点：第一类是基于知识学习形态视角的数学学科核心素养结构，强调了数学知识的重要性，将数学知识作为数学学科核心素养的重要考量维度．例如喻平指出学生数学核心素养的生成，源于对数学知识的学习，数学核心素养形成的评价应当基于知识学习的3种形态（知识理解、知识迁移、知识创新），据此对数学核心素养分为3种不同水平[1]．第二类是基于情境视角的数学学科核心素养结构，突出情境在数学学科核心素养形成过程中的重要性．例如，常磊等关注数学学科核心素养与情境之间的深刻关系，探索在情境（数学情境、科学情境、社会情境）中培养和评价数学核心素养的过程与方法[2]．第三类是基于高考内容改革的数学学科核心素养结构，充分考虑高考测评中的数学学科核心素养维度．任子朝等认为数学学科核心素养的评价应以数学知识为基础，以数学思想方法为引领，注重知识学习和运用中的素养考核[3]．第四类基于人才观和数学观的数学学科核心素养结构，将数学学科核心素养放入大人才观与数学观中，突出了学科本质特征．例如徐斌艳等在比较分析美国、芬兰、德国与新加坡等国数学素养测评的基础上，给出数学学科核心素养（数学交流与数学情感）的测评指标工具与技术[4]．

随着《深化新时代教育评价改革总体方案》的颁布，指向克服唯分数的评价局面，实施学生综合素质评价，因此，数学学科核心素养不能仅关注学生对数学知识与技能的掌握，而忽视学生数学思维与数学精神的感悟．在现有研究中，虽然谈及了数学学科核心素养测评的诸多层面，结构模型也各有异同，但是目前对数学学科核心素养结构的研究还处于起步阶段，相关研究观点更是见仁见智，对于数学学科核心素养的具体结构要素尚未达成共识，基于何种维度进行探究依然存在分歧，无论是哪一层面，哪一种视角，数学知识、数学思维、数学能力等关键词在数学学科核心素养构成要素中出现的频率较高[5]．

1.2 数学学科核心素养基本结构构建

数学学科核心素养是“四基”的整合与发展，从“四基”到数学学科核心素养是“以人为本”教育理念的时代转换，集中体现为会用数学的眼光观察现实世界、会用数学的思维思考现实世界、会用数学的语言表达现实世界，李艺等指出学科核心素养由“‘双基’层”“问题解决层”“学科思维层”3个层面构成，“‘双基’层”以基础知识和基本技能为核心，“问题解决层”以解决问题过程中所获得的基本方法为核心，“学科思维层”是在系统的学科学习中通过体验、认识及内化等过程逐步形成的相对稳定的思考问题、解决问题的思维方法和价值观[6]．该模型清晰地阐释了学科核心素养的结构与层次，在关照双基的同时强调了学科思维的教育价值，对数学学科核心素养结构分析具有一定的启示作用．

《课程标准（2017年版）》指出数学学科核心素养是具有数学学科基本特征的思维品质、关键能力以及情感、态度价值观的综合体现．在水平描述时涉及4个层面，即情境与问题、知识与技能、思维与表达、交流与反思[7]，“数学知识”包括对数学学科知识的“概念和性质”的理解，也包括学生自己给出关于概念的“定义”和关于性质的“命题”，因此，在一定程度上包括了“数学交流”，在数学思维中也涉及数学交流与表达，基本技能是学生在掌握和理解数学知识的基础上形成的程序化的操作性活动方式和心智活动方式[8]，是对学生的共性要求，这个共性要求首先是以结论或答案的正确为重点，正确的基础之上再考虑其合理性[9]，数学技能是数学能力形成的重要前提，借助问题解决可以进一步形成数学能力．而“情境”应当作为“问题解决”的一个组成部分，从波利亚（G. Polya）的《怎样解题》到哈尔莫斯（P. Halmos）提出“问题数学的心脏”，再到国际数学教育改革把问题解决作为重要议题来研究，问题解决一直备受关注．

基于以上分析，结合相关研究成果，从可测量的角度出发，关照了数学学科核心素养的4个层次，将数学学科核心素养的结构模型构成指向其知识层面、能力层面与思维层面，这与《中国高考评价体系》中所提及重点考核学生必备知识、关键能力以及学科思维相一致，将学生数学学科核心素养分为数学知识（Knowledge-K）、问题解决（Solving-S）与数学思维（Thinking-T）3个层面，其结构如图1所示．

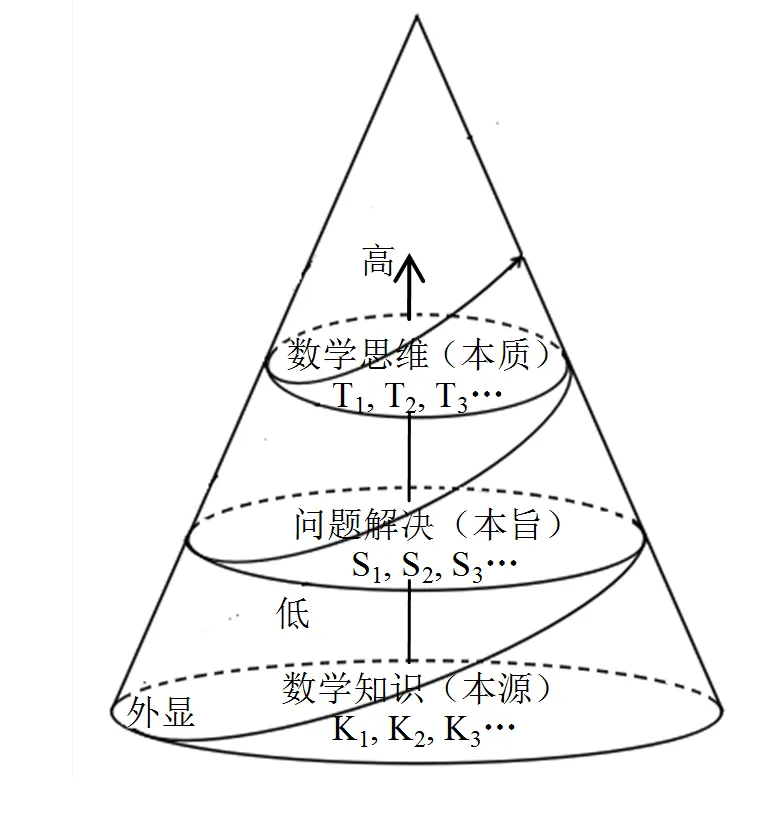
图1 数学学科核心素养三层结构

从图1可以看出，学生数学学科核心素养的三层结构，具有以下特征，第一，数学学科核心素养的内容构成具有复杂性，包含了数学知识、问题解决与数学思维3个层面，其中，数学知识是数学学科核心素养生成的本源，指向其知识层面，问题解决是数学学科核心素养教学的本旨，指向其能力层面，数学思维是数学学科核心素养内化的本质，指向其思维层面．第二，数学学科核心素养的发展水平具有双重性，其中涵盖两条“进阶线”，一条为课程目标指向的螺旋线，数学学科核心素养包含显性目标与隐性目标，其进阶过程体现了显性目标到隐性目标的转化，即从外显的数学知识到内隐的数学思维，也是从知识习得到思维内化的过程．另一条为纵向层次指向的直线，从数学知识到问题解决，再到数学思维，是由低到高，逐层进阶的．在两条“进阶线”的牵引下，数学知识、问题解决与数学思维构成相互融合的有机整体．第三，数学学科核心素养的生成路径具有多元性，数学知识以“点”分布，以“线”贯穿，以“面”支撑，以“体”呈现，形成了“数学知识块”，图1中用字母K1，K2，K3，…表示“数学知识块”，每个“数学知识块”都是不同数学知识（例如K1-1，K1-2，K1-3）之间的相互联系，学生运用知识解决问题（S1，S2，S3，…）甚至形成数学思维（T1，T2，T3，…）的路径也是多元的，称之为“KST序列”．发展路径的多元性受到学生的认知水平及其数学学习方式影响，经过学生的个性化深度学习之后，所习得的数学知识会在相关问题解决的情境中被运用并得到强化，多次运用、强化可以逐渐形成相应的数学思维．

2 数学学科核心素养生成机制

数学学科核心素养与数学知识、问题解决、数学思维之间不是简单累加的关系，数学学科核心素养的生成是数学知识、问题解决、数学思维联结融合的结果．数学知识、问题解决与数学思维在一定程度上先后作用于数学学科发展的不同水平，促进学生数学学科核心素养的进阶发展，同时数学学科核心素养的发展依赖于3者的融合状况，这就是数学学科核心素养的“融合—进阶”生成机制．

2.1 “融合—进阶”机制的结构阐释

学生数学学科核心素养不能凭空产生，其形成于数学学习与应用的过程之中．KST序列在这个过程中起到至关重要的作用．数学知识是数学学科核心素养形成的关键载体，这里所说的数学知识不是知识点的线性排列和无序堆积，是由“点”“线”“面”“体”经纬交织、融会贯通而成的数学知识块；问题解决是数学学科核心素养形成的基本场域，为数学知识提供“用武之地”，问题解决反过来帮助学生建立新的图式，形成新的数学知识，提高相应技能的熟练程度，进而生成数学能力；数学思维是在数学知识与问题解决的基础上形成的思维模式，也是数学学科核心素养的内核，数学思维的形成，预示着某一数学学科核心素养在某一水平上生成完毕．

KST序列在数学学科核心素养生成机制中的运行如图2所示，可以将其理解为数学学科核心素养三层结构在平面的投影，其中包含了数学学科核心素养的水平，每一个独立的单元代表一个数学学科核心素养．《课程标准（2017年版）》中凝练了数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六大数学学科核心素养，每个素养涵盖3个水平，因此，“融合—进阶”生成机制中含有6个单元，每一个数学学科核心素养单元都经历KST序列，实现从水平1到水平3的生成，一个数学学科核心素养生成完毕，才进入下一个数学学科核心素养的生成．需要强调的是，由于数学学科核心素养彼此独立，又相互联系，因此，其生成并非完全成线性排列，除此之外，图中的数学知识、问题解决、数学思维也是某个数学学科核心素养着重反映的内容，下面阐述数学学科核心素养生成机制中的KST序列．

（1）数学知识：数学学科核心素养生成的本源．

数学学科核心素养始于数学知识的学习，数学知识可以分为陈述性知识、程序性知识与过程性知识3类[10]，陈述性知识与程序性知识与希伯特和卡彭特的分类是一致的，即概念性知识与方法性知识，前者是对数学的概念、原理是什么的描述，指向彼此联系的网络结构，后者是对概念、原理如何运用的描述，是一系列的动作，而过程性知识是一种内隐的、动态的知识，需要学生在学习过程中体悟和习得[11]．这3类知识共同构成数学学科核心素养中的“数学知识块”．“数学知识块”是数学知识体系中的知识架构，在“数学知识块”中存在多种形式的数学知识，有些较为抽象，有些较为具体，并且这些数学知识并不在一个层次．学生在数学知识习得过程中，需要将基本生活经验与数学知识相结合，掌握知识并感悟知识所蕴含的应用价值，利用同化作用不断建立新旧知识之间的联系，从而形成“数学知识块”．

图2 学生数学学科核心素养“融合—进阶”生成机制结构

（2）问题解决：数学学科核心素养生成的本旨．

数学学科核心素养离不开问题解决，问题解决为数学学科核心素养的生成提供场域，在问题解决过程中，学生被置于一个问题情境里，当学生利用数学知识解决问题时，会根据问题情境中的信息选择相关的数学知识表征，并运用数学知识来探求问题解决的方案与策略，一旦问题获得解决，便建立了适合该情境下数学知识与解题策略的联合，这样的联合建立之后，学生所解决的不仅仅是该问题，还会掌握解决相似情境下同种类型问题的“高级规则”，这些“高级规则”使“数学知识块”不断被强化，并纳入学生的记忆库，成为认知结构的一部分，以备在类似问题或任务中再次应用，如此反复“强化—运用”，学生对数学知识的掌握会逐渐深刻．当不能解决问题时，会促使学生形成新的知识，从而拓展学生原有的“数学知识块”，直到问题解决，进而强化新形成的数学知识，通过问题解决，可以激励学生，使学生在深度学习中加深对知识的理解，学生在理论知识学习与实践应用交互过程中不断强化并拓展“数学知识块”．

（3）数学思维：数学学科核心素养生成的本质．

数学思维是数学学科核心素养的内化，具有人类一般思维的共性，同时又具有数学学科严谨性、抽象性等特征．数学思维是学生对数学概念、规则、公理等数学事实的概括与间接反应，以数量与数量关系、图形与图形关系为对象，以数学语言为工具，以数学教学活动为载体，以发现数学规律为旨要，是学生在数学学习与应用过程中产生的一种特有的数学学科精神活动．可以看出，数学思维是在数学知识与问题解决的基础上逐渐形成与发展起来的，指向数学学科核心素养的“思维层”．数学学科核心素养涵盖了理性思维、逻辑思维、创新思维、直觉思维、大数据思维，其中理性思维指向数学抽象，逻辑思维指向逻辑推理，数学运算，创新思维指向数学建模，直觉思维指向直观想象，大数据思维指向数据分析．

数学思维不像数学知识那样条理清晰，它的形成是一个长期的、复杂的、循序渐进的过程，在一定程度上具有反复性，需要在数学深度学习与运用数学知识解决问题的基础上，借助数学表达，通过多次经历、体验、感悟、内化，才能形成较为稳定的思维方式．在数学学科核心素养生成过程中，当数学思维形成失败，学生会再次重复经历类似的数学知识与问题解决，直至形成该数学思维．当某个数学学科核心素养水平1的一个数学思维形成之后，进入到第二个数学思维，当该水平中的数学思维全部形成后，进入到该数学学科核心素养的下一水平，若只含有一个水平，则整个数学学科核心素养内化为学生素养，从而进入下一个数学学科核心素养的生成．需要说明两点，其一，在实践教学中，有些内容可能会涵盖两个或两个以上的数学学科核心素养，因此学生可能是同时去生成多个数学学科核心素养的多个水平，但是对于每个数学学科核心素养、每个水平而言，都是要经历上述过程．其二，不是每个教学内容都指向数学学科核心素养的所有水平，有的内容可能只对应数学学科核心素养的一个水平，有的内容可以对应两个或3个水平．

2.2 “融合—进阶”机制的影响效应

“融合—进阶”机制在学生数学学科核心素养生成过程中表现出两个影响效应，其一为联结效应，在“融合—进阶”机制的影响下，数学学科核心素养的各个成分交织整合、渗透贯通，联结所产生的凝聚力作用于数学学科核心素养发展之中，可以说，数学学科核心素养的生成过程，就是数学知识、问题解决与数学思维相互促进、彼此统整的过程，表现为整体功能大于部分功能之和；其二为渐变效应，通过“交互—整合”机制的作用，学生的数学学科核心素养是逐渐生成的，这取决于数学学科核心素养是内隐修养（数学思维）与外在表现（数学知识、问题解决）相互影响，因此，这种内化与外化的交互使数学学科核心素养的生成是一个长期的、渐变的过程．

学生数学学科核心素养是在数学学习与应用过程中生成的，在课堂教学条件下，“融合—进阶”机制的联结效应指向融合，首先，不同的教学内容有效组织并构成秩序，相互配合、相互影响，协同作用于数学学科核心素养生成；其次，教学活动的各个层面共同作用于数学学科核心素养，促进学生数学关键能力的培养与数学思维品质的提升；最后，数学学科核心素养各个成分共同凝聚于数学学科核心素养发展之中，学生已经形成和正在形成的经验、知识、技能、能力、情感、精神等各种学科素养成分，都会在学科思维的统领下相互配合、相互协调，共同汇聚于学生的数学学科核心素养发展之中．“融合—进阶”机制的渐变效应指向进阶，一方面，数学学科核心素养的生成不是一蹴而就的，是一个循序渐进的过程，首先数学学科核心素养各要素在数量上逐渐增加[12]，例如“数学知识块”的不断拓展，学生认知结构不断完善，然后，数学学科核心素养在质量上逐渐提升，例如对于数学思维品质的提升，从量变到质变是缓慢的．另一方面，数学学科核心素养水平的发展是逐渐由低到高的，要有计划、按阶段地逐步实现，当学生数学学科核心素养要素的数量与质量达到某一节点，就会引起数学学科核心素养水平的进阶．

3 数学学科核心素养的培养路径

学生数学学科核心素养可以在数学学习与应用过程中获得，包含数学知识、问题解决与数学思维3个层次．问题解决以数学知识为基础，数学思维以数学知识与问题解决为基础，一方面，数学学习与应用指向深度学习，通过借助数学核心内容探究，帮助学生理解数学本质，构建网状数学知识结构，通过融合运用和有效迁移，使学生在掌握数学学科核心知识的基础上，培养学生问题解决能力，逐渐形成高阶数学思维．另一方面，数学学习与应用关照了学生的个性化学习，通过数学学习，人人都能获得良好的数学教育，不同的人在数学上得到不同的发展，数学学科核心素养的生成具有不同的层次与水平．其生成机制为“融合—进阶”机制，在培养学生数学学科核心素养时，应以“大概念”为生长点，构建学生学科知识结构；以“真情境”为出发点，培养学生问题解决能力；以“双向度”为切入点，提升学生学科思维品质．

3.1 以“大概念”为生长点 构建学生学科知识结构

数学学科大概念是指能够反映数学学科本质与学科特征并构成学科框架的概念，具有中心性、持久性、网状性与迁移性[13]．大概念是静态知识观转向动态知识观的产物，在传统数学课堂教学中，通常将教学的核心聚焦在数学概念、术语、公式与定理等数学知识点的传授上，这样的知识点是静态的、无关联的、碎片化的、杂乱无章的，难以实现迁移，与数学学科核心素养中对“数学知识块”的要求相去甚远．数学学科核心素养中的数学知识指向能够促进学科发展、联结学科不同领域的相关内容，在学科本质上具有共同性，在思维方式上具有同一性，在学习方式上具有生成性，在教学设计上具有一致性，这与大概念在一定程度上是相互对应的，大概念使数学学科知识具有生长力，在彼此关联之中形成新的数学知识，体现了动态知识观．

布鲁纳（Bruner. J. S）曾强调，无论教授哪个学科，一定要让学生理解该学科的基本结构，大概念的理解和运用有利于学生对数学学科结构与发展脉络进行系统把握．查尔斯（Charles. R. I）指出大概念是数学学习的核心，在数学学习过程中起着重要作用，能够将数学概念、术语、公式与定理联结成一个有机整体[14]．大概念可以统整数学学科的结构要素，从庞杂的数学知识体系中厘清数学内容的核心架构，学习这种数学基本结构有助于掌握数学学科内部及其与其它学科之间的关联[15]．将大概念作为学科核心素养教学的逻辑起点，构建数学核心知识，把握数学学科基本结构，理解数学学科本质，实现学生学习数学知识的心理认知逻辑与学科发展逻辑之间的统一，从而使学生在数学学习过程中可以像数学家那样进行思考，促进数学学科核心素养从理论层面的分析走向实践场域的教学．

3.2 以“真情境”为出发点 培养学生问题解决能力

数学学科核心素养要求学生对数学的学习不能停留在对现有知识的记忆与模仿，而是要将数学知识运用到解决问题的实践中．因此，问题解决能力是数学学科核心素养关键能力维度的重要体现，《课程标准（2017年版）》中也明确提出引导学生用数学的眼光观察现象，发现问题，用恰当的数学语言描述交流问题，用数学思想方法解决问题．问题解决能力是通过识别情境中与问题解决相关的素材，发现、分析其中所蕴含的数学问题，灵活地运用数学知识和解题策略解决问题．问题解决离不开情境，例如现实情境，数学情境与科学情境，这3类情境都可以作为数学问题背景信息的重要来源．判断一个情境是否为“真情境”的标准就在于依据该情境所提出的问题是否揭示数学的本质，好的问题情境可以唤醒学生的回忆，实现知识的迁移．将数学知识应用于问题解决，通过问题解决，也可以反过来深化学生对数学知识的理解，建立数学知识与解题策略之间联系．

问题解决以解决“真情境”里某类问题过程中所获得的方法为核心，这里的方法并不是处理某个具体问题时采用的微观、具体技能和技巧，例如几何中辅助线的技巧或者构造数列的技巧，这样的方法虽然针对性很强，但是应对的情境相对单一，不具有一般性，而且很容易忘记．一般所说的解题方法是宏观的、可迁移的、能检验的解题模式，例如波利亚的双轨迹模式、笛卡尔的万能模式、递归模式、叠加模式等，这些模式是可以帮助学生形成数学学科核心素养的．问题解决不是对先前所学知识与规则的简单应用，需要学生在解决问题时需要将已有的概念、原理、知识进行重组，并与情境中的信息相匹配，问题解决过程就是促进学生建立新规则，形成新概念，发现新原理，获得新策略的过程，一些数学学科核心素养，例如数学抽象、数学运算、数学建模、数据分析均可以在这个过程中形成．

3.3 以“双向度”为切入点 提升学生学科思维品质

数学思维与其它思维的区别是在学生经历数学学习和利用数学知识解决特定情境的问题后形成的，在形成的过程中涵盖了学生对数学问题的理解和解决的体验、认识与内化．从数学学科核心素养的三层结构来看，形成数学思维有两条线，一条是目标指向的螺旋线，表现为从外显目标到内隐目标的转换，另外一条是层次指向的直线，表现为从数学知识到问题解决，再到数学思维的转换．从横向来看，体现外显目标与内隐目标的数学对象可能会具有同构关系，从而形成一个联结式的目标网，指引数学思维品质的提升；从纵向来看，随着数学学习的不断深入，在数学知识与问题解决的基础上，学生逐渐生成数学思维，其中陈述性知识是数学思维生成的基础，程序性知识是数学思维生成的媒介，过程性知识是数学思维生成的环境，有了基础、媒介与环境，学生在问题解决过程中，就逐渐形成思维模式．

从目标指向的螺旋线来看，要注重显性目标与隐性目标的统整性，两者是有机整体，不能被人为割裂，两者是课程目标的两个方面，而不是彼此孤立的目标，是在显性目标实现的基础上，才能逐渐达成隐性目标，因此，不能将教学目标的与教学内容生搬硬套，只有实现两者整合的教学，才能实现学生数学思维品质的提升．从层次指向的直线来看，可以理解为在数学知识理解与掌握的基础上，根据知识之间的逻辑关系构成“数学知识块”，并在问题解决过程中对知识与方法再次进行概括、析取，最终形成数学思维．例如，函数单调性、奇偶性、周期性是借助函数图象的直观，用数学符号语言来刻画函数的特征与变化规律，蕴含了数学直观思维、数学抽象思维与数学逻辑思维，再如，在解决函数与方程、不等式关系等相关问题时蕴含了数学类比思维与化归思维．

[1] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19-23．

[2] 常磊，鲍建生．情境视角下的数学核心素养[J]．数学教育学报，2017，26（2）：24-28．

[3] 任子朝，陈昂，赵轩．数学核心素养评价研究[J]．课程·教材·教法，2018，38（5）：116-121．

[4] 徐斌艳，蔡金法．关于数学素养测评及其践行[J]．全球教育展望，2017，46（9）：13-24．

[5] 朱立明．我国学生数学学科核心素养研究述评[J]．数学教育学报，2020，29（2）：84-88．

[6] 李艺，钟柏昌．谈“核心素养”[J]．教育研究，2015，36（9）：17-23．

[7] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：4，74-75．

[8] 吕世虎，吴振英．数学核心素养的内涵及其体系构建[J]．课程·教材·教法，2017，37（9）：12-17．

[9] 朱立明，胡洪强，马云鹏．数学核心素养的理解与生成路径——以高中数学课程为例[J]．数学教育学报，2018，27（1）：42-46．

[10] 喻平．数学教学心理学[M]．北京：北京师范大学出版社，2018：38．

[11] 格劳斯．数学教与学研究手册[M]．陈昌平，等译．上海：上海教育出版社，1999．

[12] 李松林．学科核心素养的发展机制与培养路径[J]．课程·教材·教法，2018，38（3）：31-36．

[13] 李刚，吕立杰．大概念课程设计：指向学科核心素养落实的课程架构[J]．教育发展研究，2018，38（Z2）：35-42．

[14] CHARLES R I. Big ideas and understandings as the foundation for early and middle school mathematics [J]. NCSM Journal of Educational Leadership, 2005, 8(1): 9-24.

[15] 余文森．论学科核心素养形成的机制[J]．课程·教材·教法，2018，38（1）：4-11．

Generation Mechanism and Cultivation Path of Key Competencies of Mathematics

WU Li-sha1, ZHU Li-ming2

(1. Tangshan Normal University School of Mathematics and Computational Sciences, Hebei Tangshan 063000, China;2. Tangshan Normal University Faculty of Education, Hebei Tangshan 063000, China)

The key competencies of mathematics are constructed on the basis of the perspective of measurement, mathematical knowledge, problem solving, and mathematical thinking, and the basic characteristics of their structure are shown to be the complexity of content composition, the duality of development level, and the diversity of generation paths. The key competencies of mathematics are formed in the process of learning and application. “Integration—Progression” is the generation mechanism of key competencies of mathematics. When cultivating students’ key competencies of mathematics, we should take “big ideas” as the foundation for constructing the structure of students’ knowledge of mathematics. Take “authentic situation” as the basis for developing students’ problem-solving ability; take “two dimension” as the starting point for improving students’ mathematical thinking.

mathematics key competencies; generation mechanism; cultivating path

G632

A

1004-9894（2021）04-0025-05

武丽莎，朱立明．高中数学学科核心素养：生成机制与培养路径[J]．数学教育学报，2021，30（4）：25-29．

2021-05-10

教育部人文社会科学研究青年基金项目——高中数学教师核心素养测评模型构建与应用研究（20YJC880101）；2020年度河北省社会科学发展研究课题——河北省学科核心素养的政策理解与生成机制研究（20200501002）

武丽莎（1986—），女，河北唐山人，讲师，主要从事数学课程论研究．

[责任编校：周学智、张楠]