高中向量教学中数学思想的渗透

吕松涛，曹广福

高中向量教学中数学思想的渗透

吕松涛1，2，曹广福1

（1．广州大学 数学与信息科学学院，广东 广州 510006；2．商丘师范学院数学与统计学院，河南 商丘 476000）

针对中学向量教学重知识、轻思想的现状，以中学向量教学中渗透数学思想为导向展开讨论．分析中学数学教材中向量内容的编排思路，阐明中学向量教学渗透向量思想的必要性；从数学史中追溯向量概念产生的动因及形成过程，探讨向量对数学发展的影响，明确向量在数学中的价值，揭示向量丰富的数学内涵；分别从宏观和微观两个层面对中学向量内容进行分析，并做出教学思考；最后基于学生的认知能力提出让学生理解向量本质、领悟向量思想的课堂教学策略．

向量教学；教育目的；数学思想；教学策略

数学家怀特海论教育的目的时指出，真正有价值的教育是使学生透彻理解一些普遍的原理，这些原理适用于各种不同的具体实例[1]．也就是说，数学教育的目的不仅仅是让学生掌握数学知识，更重要的是让学生获得数学知识蕴含的数学思想，并利用数学思想解决实际问题或为进一步学习提供数学思维方法．

中学数学中的向量不同于传统的初等数学知识，它是现代数学中的重要概念，原本为大学数学的内容．因向量具有丰富的数学内涵，能为中学数学提供新的思想和方法，新课程改革将其纳入到中学数学课程．向量不仅有助于学生对几何、复数、三角函数等知识的理解，也是学习线性代数、解析几何、泛函分析等大学课程的理论基础．毫无疑问，向量内容在中学数学中有着举足轻重的地位．中学向量教学不能只把向量当作解题的工具，应让学生理解向量的本质、领悟向量所蕴含的数学思想，为大学数学的学习做好铺垫．鉴于此，以中学向量教学中数学思想的渗透为导向，分析现行中学数学教材中向量内容的编写思路，追溯向量产生的历史以及对数学发展的影响，呈现向量丰富的数学内涵，探讨中学向量的教学策略．

1 中学数学教材中向量编排内容分析

普通高中数学课程标准将中学向量内容设计为平面向量和空间向量两个部分，采取知识螺旋式上升的编排方式，分别设置在高中数学必修课程和选择性必修课程中的相关章节．课程标准指出，应从物理、几何、代数等多种角度让学生理解向量概念及其运算，并强调类比在探索向量性质、由平面向量推广到空间向量中的作用[2]．根据课程标准的内容设置要求，中国现行高中数学教材编排的向量内容大致相同．这里以人教版为例[3-4]．

在内容安排上，平面向量和空间向量的章节结构相同．在给出向量的概念后，先以向量的几何描述建立向量的线性运算、基本定理、正交分解和数量积等理论，再用向量的坐标描述重新构建这些知识，最后结合例题给出向量的应用．在情境的创设上，平面向量章节内容利用物理中的模型设置问题情境，从位移、力引入向量的概念，从运动的合成引入向量的加法，从力的分解引入平面向量的正交分解，从力做的功引入向量的数量积．空间向量的相关内容则是类比平面向量的相应知识进行引入．

教材中向量内容是根据学生的认知发展规律，按照知识的逻辑顺序编排的．结合物理问题，通过知识的分层和递进的方式，让学生在循序渐进中对向量有更加深入的理解和认识．突显向量融代数和几何为一体的性质，即向量不仅能将几何问题直接转化为算术化的分析，也能在代数中引入几何语言，将有序实数组用平面或空间中的向量来表示，每个有序数组对应于平面或空间中的一个点．尽管高中数学只是编排了平面向量和三维空间向量的知识，但是在其内容上却包含了从向量概念到向量运算体系的构造、从向量的直观几何表示到抽象的数组表示的转变，这其中蕴含着向量公理化的结构体系．这即是说，高中数学的向量内容不是碎片化的知识堆砌，而是一个描述低维几何空间性质的代数理论体系．

向量不是实数的简单扩充，它与实数运算的本质不同，是更为一般的运算对象．向量可以代表平面或空间中的点、线段，得到的是一个具有新运算规则的代数体系．因此，中学向量内容蕴含着代数的一般性质及其体系的发展．向量不仅描述了从数的算术运算到一般对象的代数运算的转变，并且其线性运算的特点构成一种应用极其广泛的数学结构，即线性空间．具有加减、数乘与数量积运算的向量集合，则能构建出完全利用代数的数量关系量化描述几何性质的代数化系统，也就是平时所说的欧几里得空间．

然而，考虑到知识的系统性和严谨性，教科书在内容编排上不可能呈现向量这些丰富的数学内涵．这就需要教师弄清楚向量的来龙去脉，明确向量在数学中的价值，进而在教学中揭示向量的本质，让学生领悟向量的思想，深化对数学的认识，有效提升学生的数学核心素养．

2 向量产生的历史及其对数学发展的影响

2.1 向量概念产生的动因

数学概念的产生通常基于两个原因，一是源于科学现实问题，二是源于数学内部的矛盾冲突．向量的产生同时兼顾了这两个方面的因素，而这两个因素又同时指向如何利用代数简单地研究几何的问题．

（1）物理中的运动问题．

运动是物理学中的基本问题，但是对它的描述几千年里一直处于模糊状态．古希腊的亚里士多德给出了描述复合运动的平行四边形法则，但他并没有做出清晰的论述．事实上，运动的本质在近代数学以前是一个复杂的问题，因为人们并不把速度或力看作有向的量[5]．牛顿在《自然哲学之数学原理》中并没有给出力、加速度的明确定义，也没有解释力和加速度是什么样的量，直接给出力等于质量乘以加速度．为了论证现实问题，数学家欧拉在1736年重新澄清和发展了牛顿的概念，引入“有方向的量”的概念[6]．欧拉认为，这个“有方向的量”不仅适用于力，也适用于速度、加速度和其它的量．

19世纪初期的科学家在研究力学问题时，开始用有向线段来表示这些“有方向的量”．然而，在解决以力学为表现的数学问题上，联系代数、分析和几何的笛卡儿坐标系统却显得繁琐而无力．其实，早在1679年莱布尼兹就发现了这个问题，他认为尽管笛卡儿的坐标系统能将几何量转化为代数方法的分析，但不是几何量之间的直接运算，有时是复杂的．这种把代数用于几何是一个正确的方法，但不是最好的[7]．在莱布尼茨的思想影响下，人们试图找出一种直接表达几何中位置、角和运动问题的方法．为了达到这一目的，必须同时考查有向线段大小和方向两个方面的性质，并找到有向线段之间的运算方法．

（2）复数的几何表示．

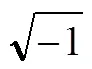
直到两个世纪后的1799年，挪威测量员韦塞尔才给出了复数的几何解释，他将复数对应于复平面的点，可用从原点到这个点的有向线段来表示[8]．而韦塞尔的主要目的是创造出一个新的几何研究方法，他认为方向的变化可由代数运算产生，也可以用符号表示，并用有向线段的乘法定义了有向线段的平面旋转变换．

2.2 向量概念的形成

为了简便地解决有向线段表示的力学问题，1832年，德国数学家格拉斯曼开始寻找一种直接用代数方法处理几何对象之间关系的系统．从这个出发点，尽管没有给出“向量”的称呼，1844年格拉斯曼直接采取有向线段的形式在《扩张论》[9]中创造了向量的基础理论．

1873年，麦克斯韦开始用四元数来处理电动力学问题, 他发现若干物理量彼此之间的关系用哈密尔顿的四元数比用笛卡儿坐标系下的方程要简单得多．但是，麦克斯韦在应用中分开处理了四元数乘积的数量和向量部分[10]．19世纪末，吉布斯和海维赛德认为在讨论物理概念时不必利用整个四元数，而只需向量部分就足够了，他们分别在格拉斯曼和哈密尔顿的基础上将向量理论系统化，创立了现代意义的向量概念及其理论体系．

2.3 向量对数学发展的影响

2.3.1 向量为几何的发展注入活力

向量集代数和几何的性质为一体，能将几何问题直接转化为算术化的分析，这有效弥补了利用笛卡儿坐标解决几何问题带来的繁琐，为人们研究几何提供了新的方法．特别地，以两个向量和的数量积=||||cos为基础，可以用与坐标无关的代数方法表示欧几里得几何的长度和角的概念[11]．1872年，克莱因利用向量将代数变换的思想引入到几何，给出几何学新的定义，即几何是研究图形在一个变换群的作用下保持不变的那些性质的一门学科[12]．这为几何学的研究开辟了新的、富有成果的途径．

利用向量线性无关的思想，格拉斯曼建立了维空间的概念，将一直囿于三维空间的几何推向了维空间的研究，让人们对几何研究的对象有了新的认识．类似于把几何从三维推广到任意维，黎曼根据向量内积和外积运算而得到的张量理论，把曲线、曲面推广到任意维流形的研究，从而开拓了黎曼几何的新篇章[13]．

2.3.2 向量扩充了代数运算的对象

代数最初是建立在数字算术运算基础上的学说[14]．人们从生产实践中不仅抽象出数的概念，也建立了数与数之间的运算关系，实现了认识上的第一次抽象．在830年，花拉子米基于解方程的形式规则给出了“代数”的名称，体现了代数是一门关于形式运算的学说．16世纪韦达发展了代数符号体系，这标志着人们在认识上实现了从算术到代数的转化．这是人类活动抽象层次的第二次飞跃，也是数学走向抽象化的重要一步[15]．

向量的出现打破了人们认为运算必须遵循“数”的规则的古老信念．不同于数的运算，向量的运算规则具有新的特点，例如两个向量的数量积不再是向量，而是一个实数或数量；当两个因子都不是零时，其数量积却可以是零．这即是说，向量形成了不同于“数系”的崭新代数体系．向量的产生是代数学从数的算术运算到代数运算转变之后的又一次质的飞跃，它使得代数保持数的运算基础的同时，把运算的对象推广成更为一般的对象．这是更高层次的抽象，使得人们对代数研究的重点开始转向运算对象所遵循的规律，因为不同的运算对象和规律描述了不同的代数体系．

2.3.3 向量促进了分析学的发展

利用数学描述物理学中量与量之间的关系，并解决物理实际问题是分析学不断发展的主要动力．向量概念的出现以及在物理学中的应用，使得人们在分析中引入向量方法，用向量来表示分析中的一些基本定理，进而将普通函数的性质推广到向量函数的研究，这开创了一个新的研究方向，即向量分析．

向量线性运算构成的维向量空间，也为分析的发展提供了一个很大的舞台，产生了极其深远的影响．建立数学知识之间的相似性与联系一直是数学家研究的重点．人们发现，由闭区间上连续函数的全体构成的集合，按照函数的加法及函数与数的乘法也有类似于向量空间的性质．因此，可以把闭区间上的连续函数看作向量，而把具体函数的研究转变为一些函数构成的集合结构的研究．将函数看作空间的一个点，可以用变换或算子的观点统一处理经典分析不同分支的具体问题[16]．若将函数看成空间的元素或点，那么算子就是定义在这种空间上并将其中的点映射为另一空间中点的映射．为了研究算子的性质，也需要研究算子的定义域所在的函数空间的结构．这种思想推动了20世纪数学中的一项重大成就——泛函分析的产生．

综上可知，向量是在问题的解决中由数学家经过抽象、概括得到的概念．向量很大程度地扩充了数学的研究范围，使原先数学研究对象中的“数量关系”和“空间形式”具备了更加丰富的内涵和更加广泛的外延．在数学的发展中，向量思想能将不同的知识用统一的语言简单地结合在一起，体现了数学的本质．数学的目的就是用简单而基本的词汇去尽可能多地解释世界[17]．

3 对中学向量内容的教学思考

通过对中学向量编排内容的分析，根据向量产生的历史及其在数学中的价值可知，中学向量的教学不能简单地按教材“就课论课”，应从宏观和微观两个层面来构建一个完整的向量理论体系的教学[18]．教师首先应从整体上把握向量内容，将章节中各个知识点串联成一个连续的知识体系，然后再具体分析每节课的教学内容，进而实现由知识点到知识体系的构建，让学生在思想方法的融合中形成稳固的知识结构．

从整体上，中学向量内容可看作从“已有的几何”到“代数化的几何”的演化过程．在这个从存在到演化的过程中，包含着数学知识的形成、代数与几何相互作用方法的更新、代数对象的一般化以及数学结构等再抽象的过程．这就要求，中学向量的教学不仅要让学生掌握教材中的知识内容，也要让学生理解应用向量定量运算描述几何定性性质的方法，深化学生对数学的认识，逐步引导学生认识到向量理论构成了一个与欧式几何体系完全等同的、能描述几何性质的代数理论体系．

从教材具体内容可知，向量章节的知识点比较多，并且每个小节的内容都有实际的物理例子或模型，这会让人误以为向量理论是由物理中不同的概念抽象得到的各种结论，而掩盖了向量结构体系以及丰富的数学内涵．另外，考虑到学生的认知能力，中学数学教材中既没有直接给出向量体系构造中的一些重要概念，比如线性相关、线性无关等概念，也没有明确现代数学意义下的代数结构体系，而是把这些概念和内容化整为零地分布到各个小节里面．这就需要以部分章节内容为单位，逐步实现从几何直观上的向量到具有运算法则的代数对象、再到现代数学结构下一般向量概念的认识．让学生理解向量的本质，掌握利用向量研究代数和几何的方法，感悟向量蕴含的现代数学思想．

4 中学向量内容的课堂教学策略

教材只是承载知识的半成品，需要教师在课堂上再发挥．知识本身也是一种承载着思想的载体，教师课堂上的任务就是透过书本知识，引导学生发现隐藏在知识背后的深刻思想[19]．基于学生的认知能力，中学向量教学应采取低起点引入、高观点分析的教学策略，以让学生理解向量的本质，领悟向量的思想，体现向量的教育价值．

4.1 以问题驱动课堂教学 明确向量概念本质

张奠宙先生认为，一切科学研究都是由问题驱动的，数学教学应该用数学被发现时的本原性问题，加以提炼和加工，呈现给学生，在数学问题驱动下呈现数学[20]．所谓的本原性问题就是促使一个概念产生或一个原理被发现的那个原始问题[21]．本原性问题是数学知识理论形成和发展的基础，体现了数学家建立数学概念和原理的初衷，能充分说明数学概念的本质．因此教师在课堂教学中必须抓住这个问题，只有围绕着本原性问题展开教学，才能让学生明白概念和原理的来龙去脉，对所学的知识有一个本质的认识和理解．

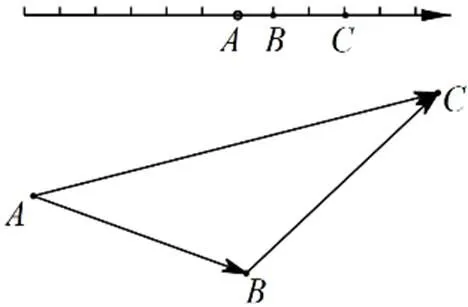
图1 示例1

向量丰富的物理背景为中学向量教学提供了现实的问题情境．借助物理中的实验或结论能帮助学生认识和理解抽象的向量概念，为向量理论的建立提供佐证．但是，在教学中不能停留在由物理问题情境直接得到向量概念的知识层面，应让学生明白为什么要抽象出这些向量理论．数学与其它自然科学的结论不同，它有着更广泛的应用性，因为抽象得到每个数学知识都蕴含着一定的数学思想．中学向量的教学既要让学生知道学什么，又要让他们知道为什么学．不然学生对向量只是表层的认知，并不能理解向量理论的本质．也就是说，无论采取什么样的教学方式，都不能偏离了数学学科的本质．美国数学家赫什曾指出，教学存在的问题并不在于教学的最好方式是什么，而在于数学到底是什么．如果不正视数学的本质问题，便解决不了关于教学的争议[22]．

在中学向量教学中，应让学生明白向量及其运算产生的本原性问题是如何利用代数简单地研究几何问题．以本原问题驱动向量教学，能引领学生思维的方向，让学生在分析和解决问题中认识到向量的本质是一个可建立运算关系的量，其几何表示是一个有向线段，具有在平面上或空间中平行移动而不失恒同性的特点．显然，问题驱动的教学过程是知识再创造的过程．弗赖登塔尔曾指出，学习数学唯一正确的方法就是实行“再创造”[23]．在问题驱动下，能让学生感悟到引入向量、将代数运算对象一般化是数学发展的必然需求，明确向量的本质和价值．

4.2 用代数研究的思路 建构向量知识体系

为便于学生理解向量理论，教材中关于向量及其运算的概念都是以几何直观的表示形式呈现的，并通过例子让学生明白利用向量的代数运算可以描述几何图形的性质．然而，如果在教学中只是以向量作为解题的工具为导向，而不注重逻辑关系下的知识结构，将会使向量理论的教学成为碎片化的知识灌输．在这种教学情形下，学生掌握的向量理论只是一个大杂烩，仅知道向量提供了一种数形结合的解题方法，而不能感知数学知识发展、完善的过程，不能认识数学化的向量理论体系．

如前所述，向量概念的产生是代数学从数的算术运算到抽象符号的代数运算转变之后的又一次质的飞跃，这是更高层次的抽象．从抽象的形式化数学概念的学习心理层面来看，学生需要依托具体的载体来理解抽象的形式化概念，而且需要把理解建立在学生非常熟悉的、牢固掌握的知识基础之上[24]．这就需要在教学时从学生已有数的知识结构出发，按照代数研究的一般思路展开．即引入研究对象，然后抽象出概念，进而分析向量之间的关系，建立向量的运算与运算律，在层层递进中引领学生构建出整体的向量知识体系．

首先，让学生认识到向量始于问题的解决，利用向量不仅能描述物理中的运动问题，而且可将问题转化为简单的数学模型．明确思维的方向，让学生感知向量是一个可以建立代数运算关系的量；其次，抽象出向量的概念，给出向量的定义及其表示．在这个环节中，不仅要关注向量的几何直观表示，更要引导学生认识到向量可以量化的代数属性，以处理好从几何直观的向量到抽象代数对象的向量概念的过渡；再次，结合学生熟悉和亲身经历过的问题，深化对向量概念的认识，建立向量之间的关系；最后，构建向量的运算，呈现向量的代数结构．因为在学习向量以前，学生非常熟悉的数的运算及运算律已包含了“结构”的雏形[15]．这里只需进一步明确，运算是代数对象性质的体现，也是建立代数对象之间关系的唯一途径，进而实现学生从算术运算到代数运算的认识转变，实现从运算到结构体系的建构．

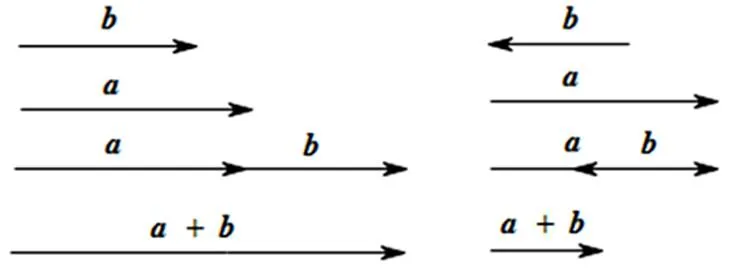
图2 示例2

4.3 合理利用类比推理 呈现向量理论体系

类比是根据两个对象的某些相似的特征属性，由其中一个对象已有的特性猜测另一个对象具有相似特性的思维方法．类比不是一般的相似性，它和其它类型的相似性之间有着本质的差别，它是思考者出于弄明白事物性质的意图而找出的相似性[25]．类比在教学中起着一个脚手架的作用，通过已有知识的类比，学生不仅能建立数学知识之间的联系，也能在原有的认知结构中找到理解和掌握新概念、新知识的“固着点”．在中学向量教学中，向量极其简洁的定义，常让人迷惑地认为理解起来简单易行，而忽视向量结构的复杂性．如果未加分析地直接给出零向量、单位向量、向量的运算等概念，学生将不能明白向量体系的特性．利用类比则能揭示出向量理论的生成过程，有效呈现向量理论体系．

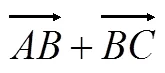
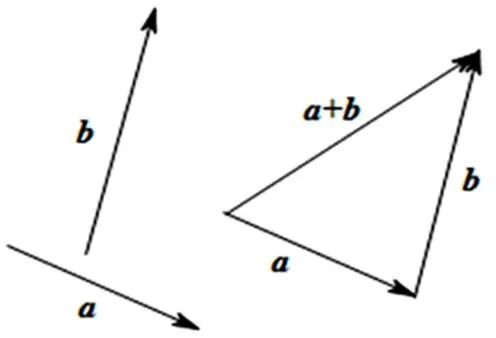
图3 示例3

在类比的过程中，学生能明确认识到加法符号“+”只是一个形式化的表示，它所代表的规则才是运算的本质．不同规则的代数运算，得到不同的代数体系．同样的道理，只要规则相同，尽管运算的对象不同，也是相同的运算．这里向量加法的运算对象是由向量代表的有向线段，它更具一般性，建立的是一个新的代数理论体系．

4.4 从现代数学观点分析内容 渗透向量思想

向量概念的产生和发展是一个从低级到高级不断抽象的过程，也是应用范围逐步扩大的过程．从最初作为物理中既有大小又有方向的量、作为复数的几何表示，到维向量空间的有序数组，再到现代数学中线性空间的元素．向量经历了一个从具体到一般、由非形式到形式化不断完善深化的过程．向量理论扩充丰富的过程体现了向量思想在数学中的应用．

菲利克斯·克莱因曾强调，中学数学教师应具备较高的数学观点，因为许多初等数学现象只有在非初等的理论结构内才能得到深刻的理解[12]．现代数学中的向量具有高度的概括性，作为线性空间中的元素，它把几何、代数和分析的研究对象融合在一起，使得数学研究的内容和方法更具一般性．中学向量知识是现代数学向量理论的基础，也可以看作是现代数学中向量概念和理论的特例．在中学向量教学中，如果从现代数学的观点分析中学向量内容，通过旁征博引让学生从看似不同的数学知识中发现它们的共性，能让学生对向量有一个深刻的认识，无形中将向量的思想渗透到知识的讲解过程．

例如，在向量线性运算的教学中，让学生理解向量将代数运算的对象推广为一般情形后，可以先明确数学抽象性的特点，即从不同的事物中发现共同特征，并研究这些共同特征，得到放之四海而皆准的原理，再用到更多的不同事物中去．接下来，从现代数学线性空间的观点，分析向量线性运算规律的适用对象．给出闭区间上的几个初等函数或几个实系数多项式，验证这些函数和多项式也满足向量加法与数乘的运算规律．进而让学生感知闭区间上的初等函数和实系数多项式与向量有着相同的线性运算，即由向量、函数、多项式分别构成的集合具有相同的代数结构．数学知识一般化的过程体现了数学知识蕴含的数学思想，虽然这里没有直接说明可把闭区间上的连续函数和实系数多项式看作向量，却已经把向量的思想潜移默化地传递给学生．他们能感悟到利用向量可以把看似不相同的事情联系起来，也正如怀特海所指出的，让学生明白所学习的向量理论适用于不同的情况．

类似地，在向量基本定理的教学中，可先从现代数学中向量线性无关的思想分析基本定理的重要价值，然后让学生理解平面或空间中的任一向量可由它的一组基底表示，进而认识到平面或空间内全体向量构成了一个集合，这个集合对向量的线性运算是封闭的，可由它的基生成．有了这些认识之后，可进一步举例让学生感悟向量的思想．比如，可用学生熟悉的多项式作为例子．学生很容易明白全体一元三次多项式构成的集合对线性运算也是封闭的，每个多项式都可以由1、、2、3唯一地表示，所以这个集合与向量构成的集合本质上相同，可由1、、2、3生成．同样地，在向量的坐标表示和数量积的教学中也可从向量的长度、正交基以及空间的几何性质进行分析，深化学生对向量的认识，体会向量概念的深刻内涵，最终让学生感悟利用向量可以用代数语言完全量化描述欧几里得几何体系．

5 结束语

数学思想与数学知识是共生的个体，不是割裂的二物[17]．每个数学概念、定理都蕴含着重要的数学思想，数学思想是数学知识的本质体现．但是，有些时候并不能直接将数学思想呈现给学生．正如文中所述，学生不易理解高度抽象、概括性的向量思想．这时可以采取通俗化的数学语言对其进行描述，在知识的教学中将向量的思想渗透给学生．在数学教学中渗透数学思想，能让学生对数学有一个深刻的认识，让他们看到数学知识的整体联系，为后续的学习做好铺垫[26-34]．反之，缺少数学思想的教学，学生掌握的知识是僵化的，只见树木不见森林，会误认为数学只是解题的技巧，不能理解数学的本质和价值．数学教学不是技能或技巧的培训，而是让学生从数学学习中获取数学思想的一门艺术．只有让学生理解了数学知识蕴含的数学思想，他们才会掌握数学思维的方式，才能切实提升学生的数学素养．

[1] 怀特海．教育的目的[M]．北京：生活·读书·新知三联书店，2002：48-49．

[2] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：25-26，41-43．

[3] 人民教育出版社课程教材研究所．普通高中课程标准实验教科书·数学必修4[M]．北京：人民教育出版社，2007：73-114．

[4] 人民教育出版社课程教材研究所．普通高中课程标准实验教科书·数学选修2-1[M]．北京：人民教育出版社，2007：83-110．

[5] MILLER D M. The parallelogram rule from pseudo-aristotle to Newton [J]. Arch Hist Exact Sci, 2017, 71 (2):157-191.

[6] TRUESDELL C. Essay in the history of mechanics [M]. Berlin Heidelberg: Springer-Verlag, 1968: 106-107.

[7] MICHAEL J C. A history of vector analysis [M]. New York: Dover Publications Inc, 1985: 1-10.

[8] M·克莱因．古今数学思想（第三册）[M]．上海：上海科学技术出版社，2002：4-5．

[9] GRASSMANN H. A new branch of mathematics: The ausdehnungslehre of 1844 and other works [M]. Chicago: Open Court, 1995: 1-9.

[10] 孙庆华，包芳勋．向量理论的产生与发展[J]．自然辩证法通讯，2011（1）：49-54．

[11] L·戈丁．数学概观[M]．北京：科学出版社，2001：86-90，103-106．

[12] F·克莱因．高观点下的初等数学（第二卷）[M]．上海：复旦大学出版社，2011：29，80-90．

[13] 胡作玄，邓明立．20世纪数学思想[M]．济南：山东教育出版社，1999：20-34．

[14] A·D·亚历山大洛夫．数学——它的内容、方法和意义（第一卷）[M]．北京：科学出版社，2001：55-58．

[15] 张顺燕．从变量数学到现代数学（续一）[J]．高等数学研究，2006，9（6）：7-11．

[16] 徐宗本．从大学数学走向现代数学[M]．北京：科学出版社，2007：1-2，30-39．

[17] 阿蒂亚．数学的统一性[M]．南京：江苏教育出版社，1995：208-211．

[18] 曹广福．把教学过程当成科研过程[J]．中国大学数学，2017（12）：11-14．

[19] 曹广福．数学课程标准、教材与课堂教学浅议[J]．课程·教材·教法，2016，36（4）：12-16．

[20] 张奠宙，张荫南．新概念：用问题驱动的数学教学[J]．高等数学研究，2004，7（3）：8-10．

[21] 曹广福，张蜀青．论数学课堂教学与评价的核心因素——以高中导数概念课教学为例[J]．数学教育学报，2016，25（4）：17-20．

[22] HERSH R. Some proposals for reviving the philosophy of mathematics [J]. Advances in Mathematics, 1979 (31): 31-50.

[23] 弗赖登塔尔．作为教育任务的数学[M]．上海：上海教育出版社，1999：102-120．

[24] 李大永，章红．基于整体把握的运算主线下的“分数指数幂”教学[J]．数学教育学报，2016，25（1）：61-66．

[25] 波利亚．数学与猜想：数学中的归纳和类比（第一卷）[M]．北京：科学出版社，2001：12-17．

[26] 李杰民，廖运章．条件概率的本质及其教学建议[J]．数学教育学报，2021，30（1）：54-60．

[27] 邓海英，严卿，魏亚楠．数学情境问题解决错误分析与评价[J]．数学教育学报，2021，30（1）：61-67．

[28] 马淑杰，张景斌．高中学生数学原有知识水平和学习认知负荷对数学课堂学习效率的影响研究[J]．数学教育学报，2021，30（2）：26-31．

[29] 江春莲，胡玲．基于APOS理论和RMI原则的二次函数图象平移教学实验研究[J]．数学教育学报，2020，29（6）：32-39．

[30] 杨怡，梁会芳，张定强．“数学探究”研究二十年：回顾经验展望[J]．数学教育学报，2020，29（6）：40-45．

[31] 邵贵明，胡典顺，柳福祥．论数学核心素养在高中数学课堂落地生根——以人教版高中“对数”教学为例[J]．数学教育学报，2020，29（6）：46-50．

[32] 郑庆全，周友士．透析数学课堂教学：“评价原理”的“认识”“应用”与“启示”[J]．数学教育学报，2020，29（6）：51-55．

[33] 王钦敏，余明芳．数学思维素养深度涵育：教学的进路与方略[J]．数学教育学报，2020，29（6）：56-60．

[34] 杜剑南，赵戌梅．基于“关键词”视角的2017年版与实验版《普通高中数学课程标准》的比较研究[J]．数学教育学报，2020，29（6）：61-68．

Integration of Mathematical Thought in the Teaching of Vector in Senior High School

LV Song-tao1, 2, CAO Guang-fu1

(1. School of Mathematics and Information Science, Guangzhou University, Guangdong Guangzhou 510006, China;2. School of Mathematics and Statistics, Shangqiu Normal University, Henan Shangqiu 476000, China)

This paper discusses the importance of vector concepts and how to integrate mathematical thought in vector teaching in view of the current situation that vector teaching in middle school attaches emphasis to knowledge rather than thought. This paper analyzes the arrangement of vector content in textbooks and expounds on the necessity of integrating vector ideas in teaching. From the perspective of historical development, the paper also points out the original problem that gave rise to vectors. By seeking the influence of vector concepts on mathematical development, this paper clarifies the value of vector ideas and reveals the rich mathematical connotation of the concept of vector. Then, it provides insights on vector teaching in middle school based on analyzing vector teaching content from the macrocosm and the microcosm. Finally, some suggestions are given for the teaching of vector and how to foster students’ understanding of the essence and mathematical thought behind vector based on students’ cognitive ability.

vector teaching; educational aim; mathematical thought; teaching strategy

2021-05-10

2020年度河南省教师教育课程改革研究项目——“互联网+”数学师范生教学技能培养模式研究与实践（2020-JSJYYB-064）；国家应用数学中学粤港澳大亚湾应用数学中心资助项目——问题驱动的中小学数学教育研究（2020B1515310020）

吕松涛（1978—），男，河南杞县人，副教授，博士生，主要从事数学教育研究．

G632

A

1004-9894（2021）04-0019-06

吕松涛，曹广福．高中向量教学中数学思想的渗透[J]．数学教育学报，2021，30（4）：19-24．

[责任编校：周学智、陈隽]