基于AdvantEdge切削工艺参数及刀具几何参数对切削力影响研究
2021-08-02赵先锋史红艳胡小龙汤朋飞
胡 波,赵先锋,史红艳,胡小龙,汤朋飞
(贵州大学机械工程学院,贵阳 550025)
0 引言
Ti6Al4V合金具有质量轻、强度高、耐高温等性能,广泛应用于飞机发动机压气机部件、火箭、导弹和高速飞机的结构件等领域[1-2],但由于其较低的导热性、较高的化学活性以及弹性模量较小等缺点,故而在进行切削时难免会出现切削温度高、刀具磨损严重等问题,以至于企业在加工过程中产生的成本较高[3]。
切削加工过程中,切削工艺参数和刀具几何参数以及环境因素等都对切削力的改变有直接或间接的关系[4-7]。关于切削力的研究最开始是由Kienzle O[8]使用经验方法得出切削过程中产生的切削力,即将横截面面积和特定能量系数乘积来表示切削力。关于切削工艺参数和刀具几何参数时怎么影响切削力这个问题国内外学者一直在研究,而绝大多数学者是在研究高速切削下的影响,这其中对高速铣削的研究居多。关于硬质合金材料的刨刀,由于其切削时独特的切削方式限制了切削速度,并在回程时不切削,故而切削效率不是很高,但刨削所需的机床、刀具结构简单,制造安装方便,调整容易,通用性强。因此在单件、小批生产中特别是加工狭长平面时被广泛应用。
本文就基于AdvantEdge对正交刨削进行有限元分析,通过29组在不同加工工艺参数下的仿真结果,采用单因素变量对仿真的切削工艺参数和刀具几何参数进行分析,总结出在低速切削下进给量、切削速度、切削深度、工件初始温度、前角、后角、刀刃钝圆半径对切削力的影响。同时找出影响切削力最主要的4个因素即切削深度、进给量、前角和钝圆半径,建立进给抗力指数公式、主切削力指数公式和切削合力指数公式,利用回归分析和最小二乘法解得各参数,最后将计算结果与仿真结果对比效果良好,具有一定的理论参考价值。
1 正交刨削切削模型的建立
1.1 材料本构模型
本文以AdvantEdge[9-10]进行仿真,本构模型为应用广泛的Johnson-Cook:
(1)
式中,A是初始屈服应力,单位是MPa;B是应变硬化常数,单位是MPa;C是特性系数;m是热软化系数;n是切削硬化指数,见表1。

表1 Ti6Al4V的JC模型参数[11]
1.2 材料的力学性能
刀具材料为硬质合金刀具,切削材料为Ti6Al4V合金,两者主要的物理性能如表2所示。

表2 工件和刀具材料的物理性能
1.3 有限元仿真模型
本文目的时为了验证正交刨削[12]时,切削工艺参数及刀具几何参数对切削力的影响,故而为了方便对比,将对29组参数进行仿真,通过查阅钛铝合金Ti6Al4V的机械强度与钢相差不多,故而吧切削过程中的硬质合金刀对钛合金看作钢对钢的过程,设置摩擦系数为f=0.2,网格为0.007。表3为仿真时会涉及到的切削工艺参数和刀具几何参数。

表3 切削工艺参数和刀具几何参数
图1为仿真过程,仿真结果含进给抗力和主切削力,切削合力通过下式计算:
(2)
式中,Fx为进给抗力,Fy为主切削力。
图1 AdvantEdge模拟切削
2 仿真结果分析
从仿真结果图(见图2)我们可以知道,整个的切削过程主要划分为两个过程即初始切削阶段和稳定切削阶段。初始切削阶段为刀具刚开始接触工件初始,由于电机的转动而使得刨刀高速旋转工件初始逐渐形成切屑,主切削力和进给抗力同时增长,但主切削力增加较快;稳定切削阶段,电机旋转稳定,刀具渡过磨合使得主切削力和进给抗力均趋于稳定,但随着各种参数的不断改变,我们可以通过将AdvantEdge仿真得到的结果依次进行控制变量分析。

图2 仿真结果
2.1 进给量对切削力的影响
图3为不同进给量(0.1 mm、0.2 mm、0.3 mm、0.4 mm、0.5 mm)下X、Y和切削合力的变化曲线图,其他设置参数分别为切削深度5 mm、切削速度15 m/min、前角10°、后角5°、摩擦系数u=0.2以及钝圆半径为0.1 mm,表4为仿真结果。从图中可以看出:随着进给量的增加,进给抗力、主切削力和切削合力都在增加,非正比变化。主要原因为:低速切削情况下,随着进给量的增加会出现积屑瘤,同时随着相同圈数所切削的长度相对变长而使得进给时的阻力变大,故而直接影响进给抗力的增加,间接影响主切削力和切削合力。

表4 不同进给量下仿真结果

图3 进给量对切削力的影响
2.2 切削速度对切削力的影响
图4是切削速度分别为15 m/min、21 m/min、30 m/min、40 m/min进行仿真所得结果,其余设置参数分别为:切削深度5 mm、进给量0.1 mm/r、前角10°、后角5°、摩擦系数u=0.2以及钝圆半径为0.02 mm,表5为仿真结果。通过图4可知总趋势为各切削力随切削速度的增加而增加。形成的主要原因为:随着切削速度的增加,积屑瘤也在渐渐增加,直接影响为各切削力的增加。
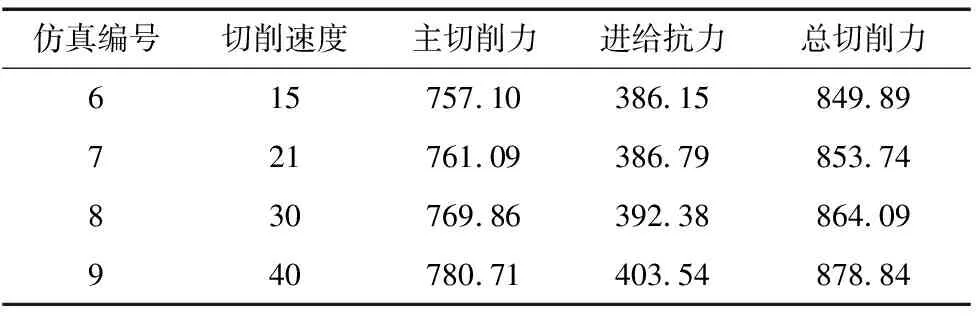
表5 不同切削深度下仿真结果

图4 切削速度对切削力的影响
2.3 切削深度对切削力的影响
图5是切削深度分别为2 mm、3 mm、4 mm、5 mm时切削深度与切削力的变化曲线图,其他参数设置为:切削速度15 m/min、进给量0.1 mm/r、前角10°、后角5°、摩擦系数u=0.2以及钝圆半径为0.02 mm,表6为仿真结果。由曲线图可知:切削力随切削深度的增加而增加且呈线性增长,其次切削深度对各个方向切削力的影响是比较大的,特别是对主切削力的影响。主要原因为:切削深度的增加切削厚度不变,而切削宽度增加,切削刃上的切削负荷也增加,最终表现为对主切削力的影响大而进给抗力相对较小。

表6 不同切削深度下仿真结果

图5 切削深度对切削力的影响
2.4 工件初始温度对切削力的影响
图6 是工件初始温度设置为20 ℃、40 ℃、60 ℃、80 ℃时的切削力变化曲线图,其余参数设置为切削速度15 m/min、进给量0.1 mm/r、切削深度5 mm、前角10°、后角5°、摩擦系数u=0.2以及钝圆半径为0.02 mm,表7为不同工件初始温度下的仿真结果。由图可知:随着工件初始温度的增加,切削力是减小的,主要原因是随着工件初始温度增加会使得工件材料“软化”,即材料的硬度和刚度会减小,最终表现为各个切削力的减小。
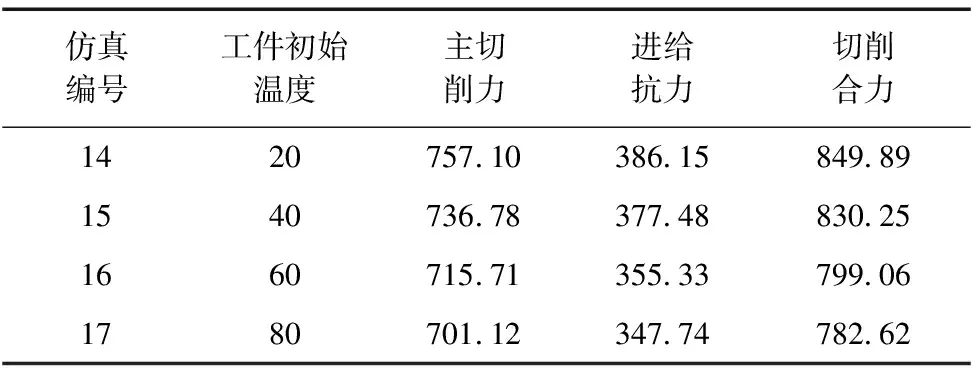
表7 不同工件初始温度下仿真结果
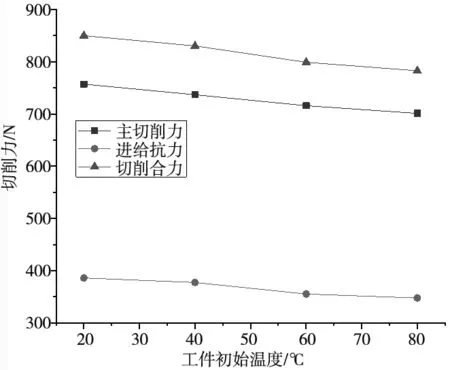
图6 工件初始温度对切削力的影响
2.5 前角对切削力的影响
图7是前角设置为5°、10°、15°、20°时的切削力变化曲线图,其余参数设置为切削速度15 m/min、进给量0.1 mm/r、切削深度5 mm、后角5°、摩擦系数u=0.2以及钝圆半径为0.02 mm,表8为不同前角下的仿真结果。由图可知各方向切削力随前角的增大而逐渐减小,且越到后面越趋于平稳,主要原因是随着前角的增大,使得剪切角增大,导致变形系数减小,即最终表现为切削力的减小。
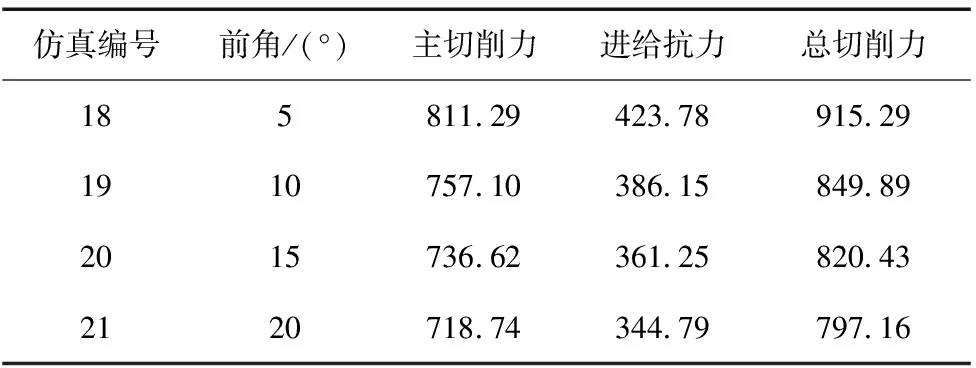
表8 不同前角下仿真结果

图7 前角对切削力的影响
2.6 后角对切削力的影响
图8 是后角设置为5°、10°、15°、20°时的切削力变化曲线图,其余参数设置为切削速度15 m/min、进给量0.1 mm/r、切削深度5 mm、前角10°、摩擦系数u=0.2以及钝圆半径为0.02 mm,表9为不同后角下的仿真结果。由图可知后角对进给抗力几乎没有影响,对主切削力和切削合力有细微影响。主要原因是随着后角的增大,会使得刀刃的锋利度增加,但同时也会使得切削刃强度降低,由于是低速切削故而切削的锋利度对切削力的影响并不明显,反而在低速情况下后角的增加会使得切削力有细微的减小。

表9 不同后角下仿真结果
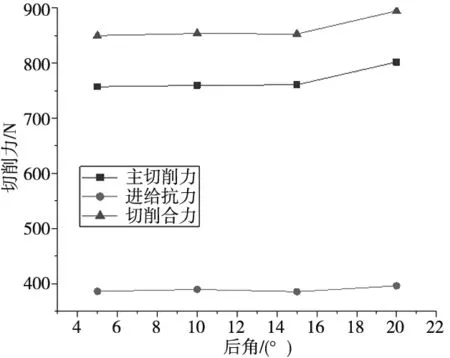
图8 后角对切削力的影响
2.7 钝圆半径对切削力的影响
图9是正交切削时钝圆半径设置为0.002 mm、0.004 mm、0.008 mm、0.1 mm时的切削力变化曲线图,其余参数设置为切削速度15 m/min、进给量0.1 mm/r、切削深度5 mm、前角10°、后角5°以及摩擦系数u=0.2,表10为不同钝圆半径下的仿真结果。由变化曲线图可知,钝圆半径对主切削力的影响相对于进给抗力的影响较小,总的趋势为随着钝圆半径的增加而增加。主要原因为:刀尖钝圆半径的增加会使得切削曲线部分的长度和切削宽度增大,但切削厚度会减薄,导致各点的主偏角减小,最终表现为钝圆半径的增加使得主切削力和进给抗力增加,而进给抗力增加明显。

表10 不同钝圆半径下仿真结果

图9 钝圆半径对切削力的影响
3 切削力预测
通过分析切削工艺参数和刀具几何参数对切削力的影响,得出进给量、切削深度、前角以及钝圆半径对切削力的影响最明显,故而建立以切削深度、进给量、前角和钝圆半径为变量,分别以主切削力、进给抗力和切削合力为因变量的指数模型公式,即:
Fx=C1apa1fb1γc1rd1
(3)
Fy=C2apa2fb2γc2rd2
(4)
F=C3apa3fb3γc3rd3
(5)
式中,Fx、Fy和F分别表示进给抗力、主切削力和切削合力;ap、f、γ和r分别表示切削深度、进给量、前角和钝圆半径;ax、bx、cx、dx分别表示切削深度、进给量、前角和钝圆半径的指数,x=1、2、3;C1、C2、C3为常数。
通过SPSS软件对仿真编号1~5、11~13、18~21、26~29共16组数据进行回归分析,得到各变量的指数,并通过最小二乘法计算出C1、C2、C3后得到指数模型公式分别为:
Fx=5052.35×ap0.165×f0.421×γ-0.043r0.503
(6)
Fy=9657.05×ap0.151×f0.761×γ-0.019×r0.262
(7)
F=13296.15×ap0.157×f0.677×γ-0.024×r0.384
(8)
为了说明3个公式的显著性,对3个建立的模型进行方差分析,分析结果见表11。

表11 方差分析
如上表所示,3个方差分析中回归平方和的自由度均为4,残差平方和的自由度均为16,通过查检验表得F0.01(4,16)=4.77,F0.05(4,16)=3.01,从表11可以看出几个模型F值远大于F0.01(4,16),概率值p=0.00<α<0.01,故回归模型拟合度很高,线性回归效果为高度显著。

(a)进给抗力预测对比

(b) 主切削力预测对比

(c)切削合力预测对比 图10 指数公式计算计算结果与仿真对比
通过计算结果和仿真结果进行对比可以发现,其相差很小,仅有极个别点会存在大误差,故而在排除一些非人为影响因素后,该模型是具有一定可借鉴性的。
4 结论
本文基于AdvantEdge软件进行有限元分析,通过29组在不同切削工艺参数和不同刀具几何参数的条件下对工件材料Ti6Al4V合金进行切削仿真, 探究了各变量对切削力的影响,故而可得结论为:
(1)切削工艺参数:各方向切削力随进给量的增加而增加,但非线性;各切削力随切削速度的增加而增加;切削力随切削深度的增加而增加且呈线性增长,其次切削深度对各个方向切削力的影响是比较大的,特别是对主切削力的影响;随着工件初始温度的增加,切削力减小。
(2)刀具几何参数:各方向切削力随前角的增大而逐渐减小,且越到后面越趋于平稳;在低速情况下后角对进给抗力几乎没有影响,对主切削力和切削合力有细微影响,主要表现为后角增加会使得切削力有细微的减小;钝圆半径对主切削力的影响相对于进给抗力的影响较小,但总的趋势为随着钝圆半径的增加而增加。
(3)通过SPSS对数据的回归分析,拟合出进给抗力指数公式、主切削力指数公式和切削合力经验公式。
基于上述结论得出在低速正交刨削时,和高速切削时会有些许一样的结论,故而在加工时我们应该针对低速、中速和高速切削设定变化范围,分段式的建立不同速度下的结论。
