基于KECA的离心泵健康状态评价方法*

王前江，陈 磊，徐向阳，岳帅旭

(郑州大学机械与动力工程学院，郑州 450001)

0 引言

离心泵是人们生产生活中常见的机器设备之一，主要用于传输液体和传递动力，城市生活给排水、农业灌溉以及化工厂液态原料传输等领域都有离心泵的参与。离心泵可靠性研究对提高其使用寿命和防止事故发生具有重要意义。健康状态评价作为离心泵可靠性研究的一个重要方向，其核心任务是对离心泵的综合性能进行定量评估和安全等级划分，直观地展现离心泵健康水平，为后续维修决策提供依据。

在设备维护过程中往往是先对设备进行一个整体把握，然后再具体分析故障类型。设备故障诊断研究成果丰富，但是同样以故障机理为基础的状态评价是一个难点，进展缓慢。目前设备状态评价的方法主要有以下几种：模糊综合评价法[1]，熵权法[2]，灰色关联分析法[3]，主成分分析法[4]，人工神经网络[5]。以上几种方法模型在离心泵状态评价中也有所应用，文献[6]将离心泵系统评价分为5个安全等级，利用AHP—模糊综合评价法给离心泵进行打分，并确定离心泵安全等级。为了摆脱AHP—模糊综合评价法在权重确定中的主观干扰，文献[7]用突变理论代替了层次分析法,提出了突变理论和模糊数学相结合的突变级数评价模型。除此之外，在离心泵状态评价中还尝试了其他方法。文献[8]将在机械方面应用较少的熵产理论引入了离心泵的能耗评价中，减小了能耗评价误差。在研究中发现，单一指标不能全面反映设备运行状态，一般是多指标参与，通过设置各个指标权重来综合评价。但是指标过多容易造成数据冗余，以至于无法定位关键信息，同时给指标赋权重增加困难。

由Jenssen Robert[9]在2010年提出的核熵成分分析(KECA)是在核主成分分析(KPCA)的基础上发展出来的一种新的降维算法。KECA与KPCA最大的区别是，KECA以信息熵的大小来选取核矩阵的特征值及特征向量，从而确定所保留的主元的。目前KECA已被成功应用到许多领域，如人脸识别[10]、产品监测[11]、化工故障诊断[12]等。针对目前离心泵运行数据冗余、非线性的特点，本文将KECA应用到离心泵状态评价中，优化数据结构同时，并根据熵值的贡献率来设置所保留各个主元的权重，提高评价的客观性。为了使输入KECA的指标更加准确，对原始信号进行经验模态分解(EMD)，利用相关系数理论剔除掉与原始信号无关的分量，提高信号的信噪比[13-14]。最后，引入健康度的概念，通过健康度直观表达离心泵的运行状态。

1 KECA算法

给定N维样本x，p(x)是概率密度函数，则其Renyi熵计算公式为：

(1)

(2)

式中，K为N×N的核矩阵；I为元素均为1的N×1的向量。Renyi熵估计可由核矩阵的特征值和特征向量来表示，将核矩阵进行特征分解K=φTφ=EDET，D为特征值矩阵D=diag(λ1,…,λN)，E为特征向量矩阵E=(e1,…,eN)，代入式(2)得到：

(3)

从以上式子可以看出，Renyi熵是N个分量的累计，特征值和特征向量对熵值的估计都有一定影响。Renyi熵较大的特征向量来确定降维空间可以最大可能的保证数据中原有信息。在此，定义一个Renyi熵相关量来选取特征向量。

(4)

核矩阵K特征分解后，将其特征值及特征向量代入式(4)并排序，得ξ1>ξ2>…>ξN。选择前m项对应的特征值作为保留主元方向并对其特征向量进行标准化，得子空间U=(β1,β2…βm)。于是，N维训练样本x的主成分为Z=Uφ，新的N维测试样本xnew的主成分Znew为：

(5)

2 基于KECA的离心泵健康状态评价实现过程

首先将原始信号进行经EMD分解,利用相关系数理论选取与原信号相关性高的IMF分量重构信号；然后将重构信号分成若干样本，计算出每个样本的15个时频域指标作为KECA的输入实现数据降维；最后以熵值贡献率作为保留主元的权重计算出健康度值，完成离心泵运行状态定量分析并根据健康度值划分安全等级。实现流程图如图1所示。

图1 基于KECA的离心泵健康状态评价实现流程图

2.1 信号降噪

EMD的本质是将信号x(t)进行平稳处理，将被分解信号的相邻峰值点间的时延定义为时间尺度，并让信号进行筛选分解。经过EMD分解后得到一系列不同频率范围的平稳信号di(t)(i=1,2,3,…,n)和残差信号r(t)。di(t)又叫信号x(t)的不同阶数的IMF分量,它们必须满足两个条件：①在时域坐标内，零点的个数与极值点的个数相等或者它们的差值为1；②在任何位置，其局部构成的最大包络和最小包络平均值为1。分解形式如下：

(6)

由于边界效应、插值误差以及过分解的原因，在EMD分解中会出现与原信号不相关的IMF伪分量，这些分量的频率成分往往与特征频带重合以至于影响特征提取，所以要将这些分量予以剔除达到降噪目的。根据相关系数原理判断IMF分量的真伪，在重构信号时剔除与原信号相关度低的IMF分量和残差信号，保留相关度高的IMF分量，从而提高信号信噪比。相关系数的计算方法如下式：

(7)

2.2 定量评价

将EMD降噪后的信号分成若干个样本，提取样本中的特征指标，离心泵的健康状态就体现在这些特征指标中。为了有效对离心泵健康状态进行定量评价，选取指标把握两个原则：第一，特征指标对离心泵的运行状态需要足够敏感；第二，特征指标变化尽量与离心泵劣化程度变化趋势同向。经筛选，选取以下15个指标作为KECA输入数据，分别是均值、标准差、方差、有效值、偏斜度指标、平均幅值、均方幅值、方根幅值、峰值、峰峰值、裕度指标、歪度指标、峭度指标、波形指标、振动烈度值。

样本标准化后求出核矩阵K，计算出核矩阵K的特征值和特征向量并带入式(4)求ξi,根据ξi对主元熵值大小排序，计算贡献率w=(w1,w2,…,wN)和累计贡献率W=(W1,W2,…,1)，贡献率和累计贡献率计算公式如下：

(8)

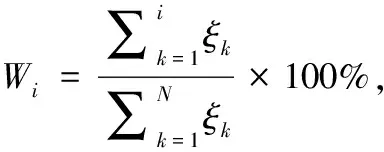
(9)

取累计贡献率为90%前m项ξi对应的特征向量U=(β1,β2…βm)，根据式(5)求得主成分Z=(z1,z2,…,zm),对于所保留主元的权值Q=(q1,q2,…,qm)为：

(10)

离心泵运行状态综合评价函数表达式：

F=ZQT=z1q1+z2q2+…+zmqm

(11)

2.3 等级划分

为了标准化离心泵健康指标，定义健康度值(HD)来表示离心泵健康状况[15]。

(12)

在式(12)的定义下，离心泵健康度的取值为0～1，HD=0时，说明离心泵为严重故障状态，HD=1时，说明离心泵为正常状态。在工程应用中，为了使维护人员更直观地了解离心泵运行状态，状态评价基于健康度被分成正常、一般、注意、危险4类安全等级。离心泵运行状态描述及健康度取值范围可以参考表1，因为工况不同，离心泵之间存在差异性，健康度取值范围的设定可以在此基础上作适当修改。

表1 离心泵健康状况的等级划分

3 实验研究

为了验证基于KECA的离心泵健康状态评价方法的有效性，选用型号为CR10-02A-FJ-A-E-HQQE的立式多级离心泵作为实验对象。离心泵转速设置为3000 r/min，采样频率为2560 Hz，采样点数设置为4096点，测点位置为泵体如图2所示，分别采集离心泵不对中、不平衡及叶轮损坏三类故障下和正常状态下的振动数据并输入方法模型，通过对比评价结果突出不同运行状态下该方法的适应性。

图2 现场实验测点图

离心泵的工作环境往往比较恶劣，造成采集的振动信号掺杂着各种不相关的成分，降低信噪比，从而影响评价结果，所以在提取故障特征前有必要进行信号降噪处理，如图3所示是未降噪处理的离心泵的振动信号。原始信号通过EMD分解可以筛选出高频成分，将EMD与相关系数理论结合又能剔除不相关成分，两种措施结合使用可充分提高信号质量，图4是经过EMD降噪后的振动信号。

图3 离心泵的原始振动信号

图4 经过EMD降噪后的振动信号

将重构的信号每50个数据点分为一组，分成若干组样本，提取每组样本的15个特征指标作为KECA的输入，选取的核函数为高斯核函数，通过调节核参数改变特征空间，优化评价结果的稳定性和准确性。保留累计超过90%的主元，代入离心泵运行状态综合评价函数表达式计算得分，并于KPCA方法作对比，两种方法的评分结果如图5、图6所示。由图可知，KECA和KPCA两种方法对离心泵的各种状态都有一定的区分度，但相对KPCA，基于KECA的离心泵健康状态评价方法更加准确和稳定，所以KECA更有优势。

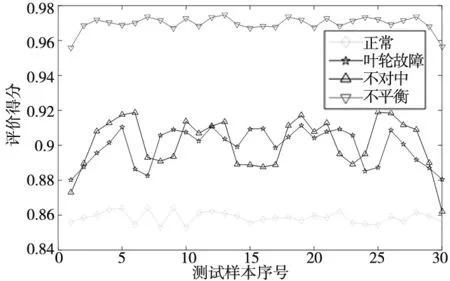
图5 基于KECA的离心泵健康状态评价

图6 基于KPCA的离心泵健康状态评价

图7 离心泵健康度及安全等级

4 总结

KECA是将原始数据映射到高维特征空间，以信息熵的大小来选取核矩阵的特征值及特征向量，从而确定所保留的主元。将KECA算法引入到离心泵健康评价中，首先利用EMD对数据进行降噪预处理，然后利用KECA提取出熵值较高的主元，并根据熵值的贡献率来设置所保留各个主元的权重，最后以健康度值来定量评价离心泵运行状态。实验结果表明，基于KECA的离心泵状态评价方法在降低维度的同时，能够有效提取出离心泵运行数据中的关键信息，实现对离心泵的健康状态客观评价，证明了该方法的科学性和有效性。在接下来的研究中，还可以扩大KECA的输入指标维度，更全面地提取离心泵的运行状态信息，从而进一步提高健康评价的准确性。