基于滚道型面参数和摩擦力矩匹配的滚珠丝杠副高效装配*

吴 剑，欧 屹，王 凯

(南京理工大学机械工程学院，南京 210094)

0 引言

单螺母滚珠丝杠副通过控制螺母导程大小控制滚珠丝杠副预紧力大小，具有传动效率高、定位精度好、反向间隙小等优点[1-2]，被广泛应用于机床行业，但由于加工误差不可避免，滚珠丝杠、滚珠螺母总是存在型面误差，型面误差将直接影响滚珠丝杠副的使用性能。摩擦力矩作为滚珠丝杠副最重要的性能之一[3]，其优劣直接决定滚珠丝杠副的使用情况。在滚珠丝杠副磨损导致摩擦力矩衰退后，常采用更换滚珠的方式调整预紧力，从而调整摩擦力矩。因此，研究型面参数以及滚珠大小对滚珠丝杠副摩擦力矩的影响具有重要意义。

近年来，多通过预紧力计算摩擦力矩。程光仁[4]提出了目前国内通用的滚珠丝杠副预紧力与空载扭矩(即DIN ISO 3408-3中的规定方法测得的摩擦力矩)的经验公式，该公式没有考虑接触角和摩擦系数对摩擦力矩的影响，也没有说明测量条件。胡建忠等[5]通过坐标变换计算双螺母滚珠丝杠副轴向预紧力，但计算中并未考虑误差因素；崔高尚等[6]分析了双螺母滚珠丝杠副预紧力与垫片预紧量的关系，但并未说明预紧量的计算方法；Zhou C G等[7]基于经验公式提出新的摩擦力矩计算模型，但理论模型假设各滚珠载荷、接触角均匀分布会造成偏差。陈斌斌等[8]通过考虑到滚珠丝杠副的接触角、螺旋角、有效承载滚珠个数、滚珠直径和滚道的型面参数等因素，建立了基于滚珠过盈量的滚珠丝杠副预紧力计算模型，但其型面参数只是理论的型面参数，未测量出滚珠丝杠和滚珠螺母实际的型面参数。以上对摩擦力矩的研究均未考虑丝杠、螺母型面误差的影响。

本文在前人对滚珠丝杠摩擦力矩研究的基础上，通过丝杠螺母型面检测装置检测出精确的型面参数，从而计算出滚珠的精确变形，根据赫兹接触理论和预紧力与摩擦力矩的关系建立滚珠丝杠副摩擦力矩计算模型，并通过滚珠丝杠副摩擦力矩计算公式，计算出对摩擦力矩失效的滚珠丝杠所需要的滚珠大小，对其摩擦力矩进行恢复。

1 接触变形分析

1.1 滚珠接触状态

滚珠丝杠副在预紧力或工作载荷的作用下，滚珠与丝杠滚道面之间、滚珠与螺母滚道面之间会产生一定的弹性接触变形量[9]，单螺母滚珠丝杠副在不受外部载荷作用的情况下，滚珠与滚道的法向截面接触如图1所示。以螺母变导程中心点将螺母分为左右两个半区，滚珠在螺母左半区和右半区的接触点位置刚好相反。在螺母和丝杠螺距相等的情况下，丝杠滚道理论滚珠圆心Os与螺母滚道理论滚珠圆心On应在同一径向上，由于螺母变导程螺距大于pnh丝杠螺距Psh，螺母滚道偏移位移量σα，又因为丝杠中径与螺母中径不等会产生偏移量σh，丝杠、螺母滚道挤压滚珠产生预紧力。在预紧力作用下，其产生的变形为弹性变形，可采用赫兹理论对其接触变形进行分析[10]。

则法向平面内单螺母滚珠丝杠副中螺母相对于丝杠有一偏移量ΔS为：

ΔS=Pnh-Psh

(1)

则左半区丝杠滚道理论滚珠圆心与螺母滚道理论滚珠圆心的偏移量为：

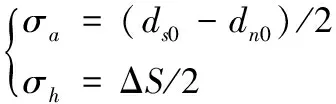
(2)

其中，σα为丝杠滚道理论滚珠圆心与螺母滚道理论滚珠圆心的法向平面的轴向偏移量，σh为丝杠滚道理论滚珠圆心与螺母滚道理论滚珠圆心的法向平面的径向偏移量,ds0为丝杠中径，dn0为螺母中径。

图1 单螺母滚珠丝杠滚珠接触状态

1.2 滚珠法向变形

由于螺母左右半区，滚珠变形原理相同，对左半区滚珠变形进行分析，滚珠法向变形如图2所示，rsL为丝杠左圆弧曲率半径，rnR为螺母右圆弧曲率半径，OsL为丝杠左圆弧圆心，OnR为螺母右圆弧圆心，esL为丝杠左圆弧轴向偏心距，hsL为丝杠左圆弧径向偏心距，enR为螺母右滚道轴向偏心距，hnR为螺母右圆弧径向偏心距，Ods为丝杠滚道理论滚珠圆心，Odn为螺母滚道理论滚珠圆心，O为滚珠受挤压后滚珠圆心，Δx为丝杠法向滚道理论滚珠圆心与螺母法向滚道理论滚珠圆心的轴向偏差，Δy为丝杠中径与螺母中径差。

图2 滚珠法向截面接触变形简图

根据几何关系，此时滚珠的法向变形量与接触角为：

(3)

其中，α为接触角，δ为滚珠法向变形量。

1.3 赫兹接触理论

根据赫兹接触理论，弹性体接触时弹性变形量为：

(4)

式中，K(e)为第一类完全椭圆积分，ma为与椭圆偏心率有关的系数，μ1、μ2为泊松比，E1、E2为材料弹性模量，P为法向载荷，∑ρ为接触点主曲率和。

根据赫兹接触理论，接触点处的主曲率和为：

∑ρ=ρ11+ρ12+ρ21+ρ22

(5)

主曲率函数为：

(6)

滚珠丝杠副中滚珠与丝杠和螺母滚道面接触点的曲率如表1所示。

表1 滚珠与滚道面接触点的曲率

表1中，Rb为滚珠直径，frs为丝杠左圆弧滚道半径与滚珠半径之比，frn为螺母右圆弧滚道半径与滚珠半径之比，ds0为丝杠中径，dn0为螺母中径，α为接触角。

将丝杠和螺母滚道面接触点的曲率带入式(2)、式 (3)可得滚珠与丝杠滚道接触处的弹性变形量δS为：

(7)

式中，Ks(e)为丝杠圆弧的第一类完全椭圆积分，mas为与椭圆偏心率有关的系数，μ1、μ2为泊松比，E1、E2为材料弹性模量，P为法向载荷，∑ρs为滚珠与丝杠接触点处主曲率和。

滚珠与丝杠滚道接触处的弹性变形量δN为：

(8)

式中，Kn(e)为丝杠圆弧的第一类完全椭圆积分，mas为与椭圆偏心率有关的系数μ1、μ2为泊松比，E1、E2为材料弹性模量，P为法向载荷，∑ρs为滚珠与丝杠接触点处主曲率和。

2 摩擦力矩计算模型

2.1 预紧力计算模型

如图3所示为滚珠与丝杠接触点受力分解图，Fn为合力，Fa为轴向力分量，Fr为径向力分量，Ft为圆周力分量。

(9)

其中，λ为丝杠螺旋升角。

图3 滚珠与丝杠接触点受力分解图

滚珠法向的总变形量δ为：

δ=δS+δN

(10)

将式(9)、式(10)带入式(7)、式(8)可得预紧力Fp与变形量δ的关系为：

(11)

其中，n为滚珠丝杠副有效承载滚珠个数。

2.2 摩擦力矩计算模型

Zhou C G提出了预紧滚珠丝杠副预紧力与空载扭矩(即DIN ISO 3408-3 中的规定方法测得的摩擦力矩)的关系[7]，滚珠丝杠副预紧力与摩擦力矩的关系如式(12)所示。其中，Mf为摩擦力矩，μ为摩擦系数，rm为丝杠轴的半径，rb为滚珠半径。将式(1)～式(3)、式(5)、式(10)、式(11)带入式(12)可以得到基于滚道型面参数的滚珠丝杠副的摩擦力矩：

(12)

3 实验分析

3.1 摩擦力矩计算模型实验验证

为了验证摩擦力矩理论模型的准确性，通过测量丝杠、螺母准确的型面参数并更换不同直径滚珠重新装配后测量滚珠丝杠副摩擦力矩。

如图4所示为滚珠丝杠型面检测试验台，该试验台由电机、位移平台、直线光栅尺、光幕式传感器等组成。安装好待测丝杠后，通过转台旋转丝杠螺旋升角，通过电机带动位移平台从而带动光幕式传感器，测量出丝杠母线的法向轮廓的坐标，通过软件计算得到滚珠丝杠的型面参数。

图4 滚珠丝杠型面检测试验台

如图5所示为滚珠螺母型面检测试验台，该试验台由水平电机、竖直电机、水平位移平台、竖直位移平台、直线光栅尺、激光位移传感器、三坐标位移平台、V型块等组成。将待测螺母放在V型块上，通过三坐标位移平台，将螺母旋转一个螺旋升角，通过竖直电机和水平电机将激光位移传感器测量头调整到合适的位置，通过水平电机带动测量头测量螺母内滚道，测量出螺母母线的法向轮廓的数据，通过软件计算得到滚珠螺母的型面参数。

图5 滚珠螺母型面检测试验台

如图6所示为滚珠丝杠副摩擦力矩试验台，该试验台由伺服电机、工作台、一对滚动直线导轨和力传感器组成。伺服电机驱动丝杠旋转，工作台由滚动直线导轨支撑，可沿轴向移动，工作台装有可与丝杠滚道啮合的支撑座，使丝杠在无附加力的条件下带动工作台轴向移动。滚珠丝杠副螺母法兰装有螺栓，伸出法兰端面的螺栓与力传感器接触，通过软件计算得到滚珠丝杠副的摩擦力矩。

图6 滚珠丝杠副摩擦力矩试验台

选用THK生产的单螺母变导程预紧滚珠丝杠副，型号为BIF4010-7，1级精度。滚珠丝杠副中，有效承载的滚珠个数约为60个。

利用丝杠型面检测试验台和螺母型面检测试验台对样件进行检测，测得螺母左半区右圆弧的型面参数为：rnR为3.489 mm，enR为0.201 2 mm，hnR为0.236 6 mm，变导程螺距为10.030 5 mm，dn0为41.783 mm。测得丝杠左圆弧型面参数平均值为：rsL为3.504 9 mm，esL为0.229 7 mm，hsL为0.241 1 mm，平均螺距为10.018 mm，ds0为41.785 mm。

标准大小的钢球为6.35 mm，更换不同直径的钢球来改变滚珠丝杠副的摩擦力矩，通过滚珠丝杠副摩擦力矩试验台测量出不同直径滚珠滚珠丝杠副摩擦力矩。由于丝杠和螺母型面参数变化不大所以用型面参数平均值来计算摩擦力矩，所以将平均型面参数带入式(13)得到理论的平均摩擦力矩。实验测得摩擦力矩与理论测得摩擦力矩如表2所示。

表2 理论摩擦力矩与实际摩擦力矩比较

将理论摩擦力矩与实际摩擦力矩进行比较，结果如图7所示。

图7 摩擦力对比分析

根据表3中的分析和图7中曲线的对比，可以看出在不受外部载荷情况下，理论摩擦力矩与实际测得的摩擦力矩基本重合，理论摩擦力矩与实际摩擦力矩的相对误差在5.96%之内，理论模型与实际预紧力的一致性较好。

3.2 基于型面参数的滚珠丝杠副快速装配

滚珠丝杠副使用一段时间后由于滚道型面磨损导致摩擦力矩衰退，通常选择增加滚珠直径来恢复摩擦力矩。为了更加高效的选择滚珠大小，可以先用丝杠、螺母型面检测装置，检测出磨损后丝杠、螺母的型面参数，再通过公式算出所需摩擦力矩大小情况下最适合的滚珠大小，从而实现更加高效的装配。

为了验证取了一个摩擦力矩减小的滚珠丝杠副，先检测它的型面参数，测得螺母左半区右圆弧的型面参数为：rnR为3.498 4 mm，enR为0.209 3 mm，hnR为0.240 1 mm，变导程螺距为10.029 5 mm，dn0为41.773 mm。测得丝杠左圆弧型面参数平均值：rsL为3.511 8 mm，esL为0.230 5 mm，hsL为0.247 3 mm，平均螺距为10.017 1 mm，ds0为41.771 mm。未减小前测得其摩擦力矩为1.177 9 Nm。原有滚珠大小是6.35 mm。通过公式(13)计算出在滚珠过盈量为3.3 μm时理论摩擦力矩为1.254 5 Nm。将摩擦力矩减少的滚珠丝杠换上过盈量为3.3 μm的滚珠，通过滚珠丝杠副摩擦力矩试验台测得其摩擦力矩为1.214 5 Nm，与未磨损前摩擦力矩差1.38%，满足要求。大大减少了装配工人试错的时间，提升了装配效率。

4 结论

基于丝杠螺母型面检测试验台，测量出丝杠螺母精确的型面参数，并通过对滚珠丝杠副接触变形分析和滚珠受力平衡分析，建立了单螺母滚珠丝杠副摩擦力矩计算模型。与实验结果相比较可知，理论摩擦力矩与实际摩擦力矩，相对误差在5.96 %之内。该理论可应用于摩擦力矩衰退的滚珠丝杠副快速恢复，准确性较高，且与人工反复适配目标预紧摩擦力矩相比，提高了工作效率。