基于刀-屑摩擦与切削速度关联模型的切削力数值分析*

郭建英 吕 明

(①太原理工大学矿业工程学院，山西 太原030024;②太原理工大学机械工程学院，山西 太原030024)

在切削加工中，提高切削速度可以提高生产效率，改善加工精度，减小切削阻力，但切削力随切削速度提高而减小的确切机理仍不清楚［1-2］。切削时，切屑第一变形区内工件材料的剪切变形抗力与第二变形区内的刀-屑摩擦阻力是产生切削力的主要来源。当切削速度提高时，第一变形区温度升高会使工件材料变形抗力减小，第二变形区温度升高会使切屑底层材料热软化，刀-屑摩擦系数减小［3-4］。

切削是复杂的物理力学变化过程，高效精确的数值分析技术已成为研究切削机理的一种重要手段。Lin Z C［5］采用有限元法研究了3 种不同低切削速度(低于0.6 m/s)时切削力的变化特性，在其建立的有限元模型中，只考虑工件材料的变形阻力随高温热软化而减小，未考虑刀-屑摩擦的影响，因此其切削力模拟值的误差较大。Moufki A［6］认为随着切削速度提高，工件材料高温热软化，刀- 屑摩擦系数减小。因此，他采用刀-屑摩擦系数随切削温度减小的关联模型，研究切削速度对切削力的影响特性。然而，在切削过程中，可以引起切削温度升高的因素不仅有切削速度，还有刀具前角等其他参数。因此，刀-屑摩擦与切削温度的关联模型不能直接用于研究或解释切削速度对切削力的影响机理。

本文通过直角切削实验，测试在形成连续切屑的条件下，切削力随切削速度的变化特性;并建立刀-屑摩擦系数与切削速度的关联模型，采用该模型对不同切削速度时的切削过程进行热力耦合数值分析。将切削力分析值与实测值进行比较，分析切削力随切削速度增大而减小的主要原因，为建立准确的切削过程数值分析方法提供参考。

1 切削力实验测试

1.1 直角切削实验

在CA6140 车床上对Q235 钢进行直角切削实验。为了满足直角切削条件，将工件预先车出深槽，并用直线尖角刀刃进行干式切削。实验过程中，刀具材料为硬质合金，切削速度为0.042～2.09 m/s，刀具前角γo分别取20°和30°，刀具后角α0为6°～7°，切削深度ac为0.3 mm，切削宽度aw为2.5 mm，采用电阻应变片式三向测力仪测量切削主力。

1.2 实验结果

表1 和表2 显示了在刀具前角分别为20°和30°，不同切削速度时切削力的实测值。从表中可以看出，随着切削速度的提高，切削力呈明显的减小趋势。

表1 不同切削速度时主切削力实测值(刀具前角γo =20°)

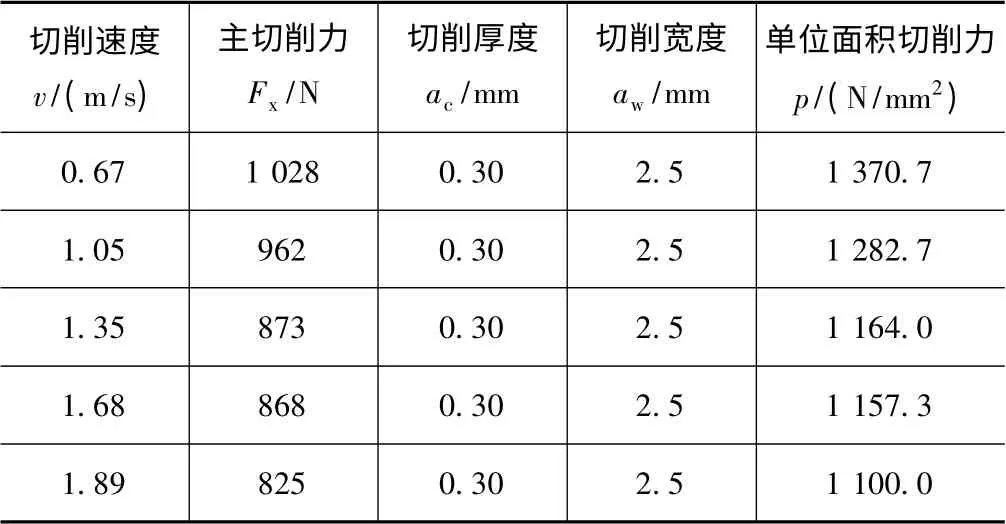
表2 不同切削速度时主切削力实测值(刀具前角γo =30°)

图1 为实验过程中提取的不同切削速度时切屑的外观形态。从图中可以看出，当切削速度为0.042 m/s时，切屑卷曲外表面很粗糙，表明切屑流出时切屑底层材料与前刀面有粘接剪切现象，即刀-屑间摩擦系数较大，表现为粘接摩擦;当切削速度增大到0.67 m/s时，切屑卷曲外表面粗糙度值有所减小;而当切削速度增大到2.09 m/s 时，切削卷曲外表面非常光滑，表明这时切屑与前刀面间摩擦系数较小，表现为滑动摩擦。该结果表明，随切削速度的提高，刀-屑摩擦系数会减小。

2 切削过程热力耦合有限元分析

2.1 有限元模型

采用通用显式有限元程序ANSYS/LS -DYNA 对低碳钢Q235 直角切削过程进行热力耦合数值分析。金属切削过程中，切削层材料会发生大变形，并伴随高的应变率。当切削速度较高时，还会产生较高的切削温度。为了考虑这些因素对材料特性的影响，切削层材料模型采用带热效应的弹-粘塑性本构关系，即材料的流动应力依赖于应变、应变率和温度。这时，材料的单轴应力应变曲线函数为［7］

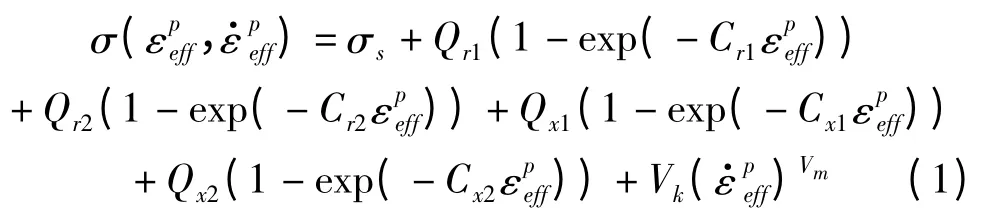
式中:σs为材料初始屈服应力为有效应变率，为有效塑性应变，Qr1、Qr2、Cr1、Cr2为各向同性硬化参数，Qx1、Qx2、Cx1、Cx2为动态硬化参数，Vk、Vm为材料应变率相关的黏性参数，应变率效应通过Cowper and Symonds 模型来定义，它对屈服应力的缩比因数为:

Vk、Vm的值为:

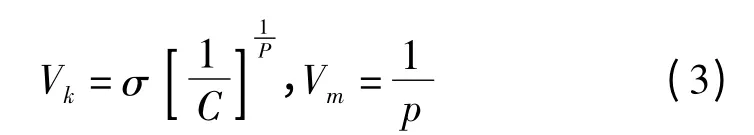
式中:C、p为Cowper -Symonds 模型中的应变率常数，C=40.0，p=5.0。工件材料的弹性模量E、初始屈服应力σs、热膨胀系数α 随温度的变化关系如表3 所示。由于刀具的弹性模量较高，因此模型中将刀具设为刚体，仅对其进行热传导分析。表4 为工件与刀具材料的物理特性。

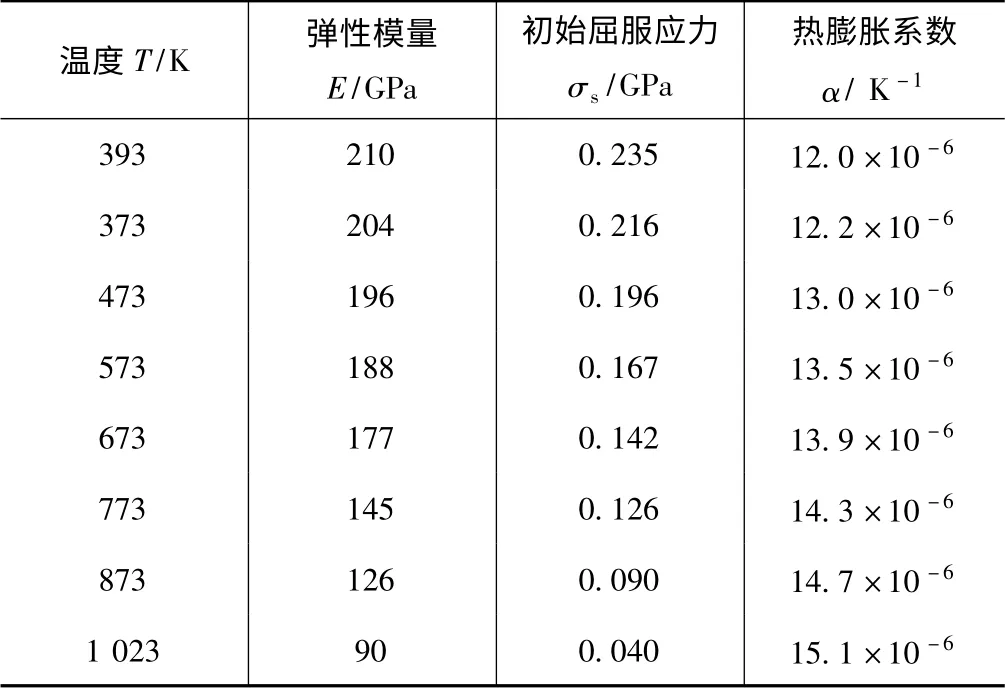
表3 低碳钢Q235 在不同温度下的热粘性特性

表4 工件与刀具材料的物理特性

在有限元模型中，采用面-面固连断开接触算法模拟切屑的形成过程;采用修正的库仑摩擦模型来计算刀-屑间的摩擦应力f:

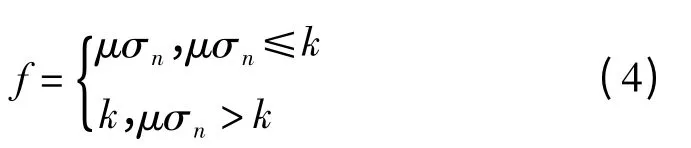
式中:σn为刀-屑接触界面的正应力;μ 为刀-屑摩擦系数;k为粘性摩擦系数，用于限制最大摩擦应力，k为工件材料屈服应力。

2.2 刀－屑摩擦系数为恒定值时切削力数值分析

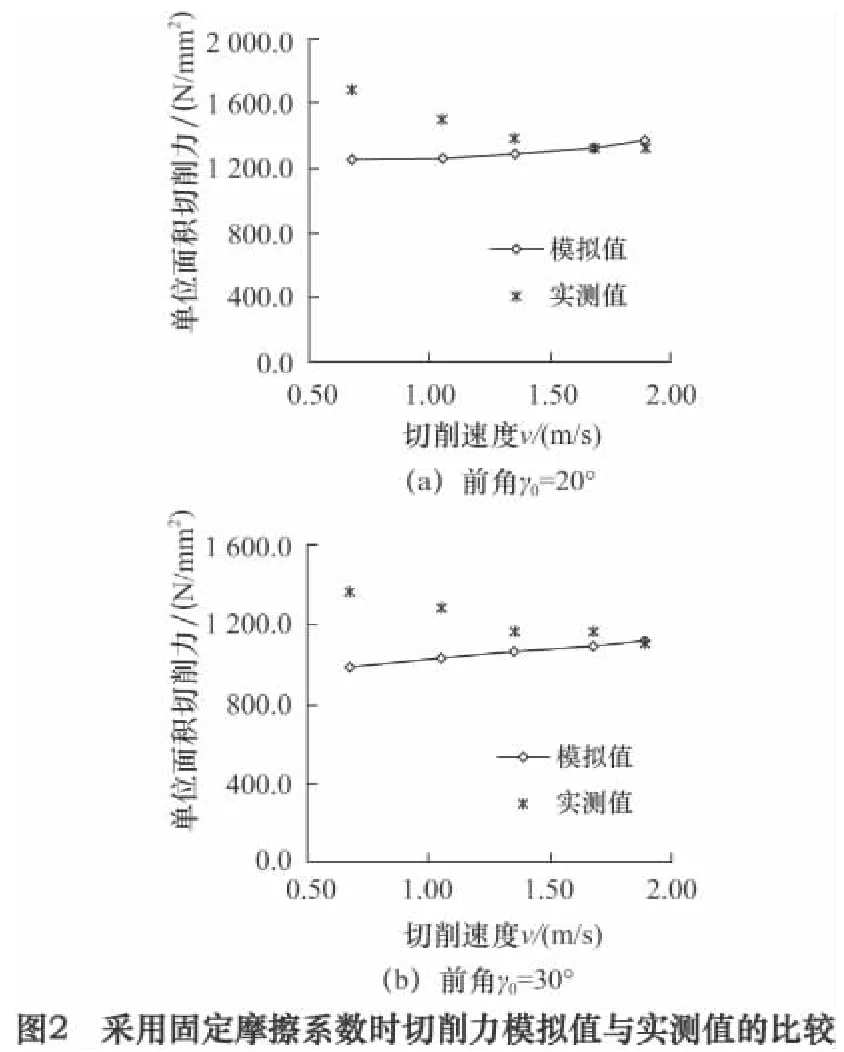
切削过程中，提高切削速度，工件材料的变形抗力会随切削温度的升高而降低。为了单独考察工件材料变形抗力的下降对切削阻力的影响程度，本文先将刀-屑摩擦系数取为一恒定值，即μ =0.4，对不同切削速度时的切削过程进行热力耦合分析。切削力模拟结果见图2。从图中可以看出，随着切削速度的提高，切削力的模拟值没有降低，反而有小幅升高。

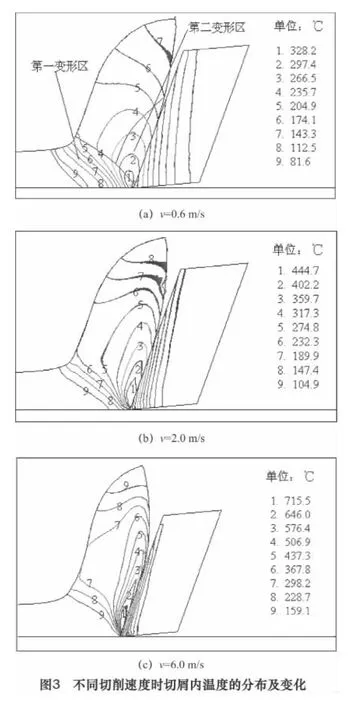
该结果可以从切屑内的温度分布及其随切削速度的变化规律得到解释。图3 显示了刀具前角为20°，切削速度分别为0.6 m/s、2.0 m/s、6.0 m/s 时切屑内温度场的分布及变化。从图3a 可以看出，最高切削温度位于第二变形区切屑底层与前刀面接触区域内，切屑内部温度逐渐下降。而在第一变形区，切削温度呈带状分布，且数值较低。比较图3a、b、c 可以发现，当切削速度从0.6 m/s 增加到6.0 m/s 时，第二变形区内最高温度由328.2 ℃增大到715.5 ℃，增幅为118%;而第一变形区内切削温度增幅很小，其数值始终保持在100～250 ℃左右。

切削温度的分布及变化情况表明，随切削速度的提高，第一变形区内工件材料的剪切变形抗力不会有显著的减小;反而由于切削速度提高，材料应变率增大，使得切削阻力小幅增大。再结合图1 中不同切削速度时切屑的变形形态可以看出，第二变形区内切屑底层材料由于温度的大幅上升而热软化，塑性增加，刀-屑间摩擦系数减小，这可能是导致切削力随切削速度提高而减小的主要原因。

2.3 建立刀－屑摩擦系数与切削速度的关联模型

图2a 的数据显示，在刀具前角为20°的情况下，当切削速度为0.67 m/s 时，单位面积切削力的模拟值远小于实测值，其误差高达-29.45%;当切削速度逐渐增大为1.05 m/s 和1.35 m/s 时，单位面积切削力的模拟值仍小于实测值，但其误差在逐渐减小;当切削速度提高到1.68 m/s 时，该误差值达到最小，为0.96%。同样，在刀具前角为30°的情况下，(见图2b)，当切削速度由0.67 m/s 提高到1.89 m/s 时，单位面积切削力模拟值的误差由- 28.12% 降低到1.68%。这些数据表明，当切削速度为0.67 m/s 时，实验中刀-屑摩擦系数的真实值远大于0.4;随切削速度提高，刀- 屑摩擦系数减小;当切削速度达到1.68 m/s 时，刀-屑摩擦系数真实值约为0.4。

因此，本文建立刀-屑摩擦系数μ 随切削速度v呈指数下降关系的数学模型:

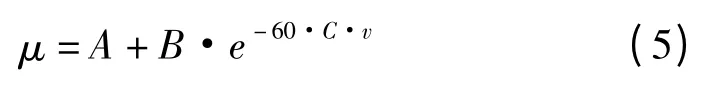
式中:A、B、C为常数，其中A=0.2，取为钢-软钢间的静摩擦系数;B=0.8，取为钢-钢间滑动摩擦系数［8］;C=0.014，该值是按照表1、表2 中单位面积切削力实测值的变化趋势，并进行曲线拟合后确定;v为切削速度，m/s。

2.4 基于刀－屑摩擦系数与切削速度关联模型的切削过程数值分析

为了验证模型(5)的准确性，在切削有限元模型中，将式(5)代入式(4)来计算切屑与前刀面间的摩擦应力f，再对切削速度分别为0.67 m/s、1.05 m/s、1.35 m/s、1.68 m/s、1.89 m/s 时的切削过程进行热力耦合数值模拟。图4 显示了刀具前角为20°和30°时，切削力随切削速度的变化情况。从两图中均可看出，随着切削速度提高，切削力模拟值减小，其变化趋势与实测值的变化趋势一致;当刀具前角γo为20°时，切削力模拟值的最大误差为-6.74%，最小误差为-0.63%;当刀具前角γo为30°时，切削力模拟值的最大误差为-8.21%，最小误差为-3.35%。

该结果表明，本文所建立的刀-屑摩擦系数与切削速度呈指数下降关系的数学模型，可用于描述在形成连续切屑的条件下，低碳钢切削速度对切削力的影响特性，也可实现对不同切削速度时切削力数值的准确预测。

3 结语

(1)切削过程中，在形成连续切屑的条件下，当提高切削速度时，第一变形区内温度较低且增幅很小，由其引起的工件材料变形抗力的降低，对切削力影响很小;而第二变形区温度较高且增幅较大，与前刀面相接触的切屑底层材料由于高温热软化，塑性增加，刀-屑间摩擦系数减小，是切削力减小的主要原因。

(2)建立了刀-屑摩擦系数与切削速度呈指数下降关系的关联模型。采用该模型对不同切削速度时的切削力进行数值分析，刀具前角为20°时，切削力模拟值的最大误差为-6.74%，最小误差为-0.63%;刀具前角为30°时，切削力模拟值的最大误差为-8.21%，最小误差为-3.35%。

［1］姚永琪，郭乙木，朱凌，等. 高速切削时摩擦系数对切削影响的数值模拟［J］. 工程设计学报，2004，11(1):31 -36.

［2］Bäker M. Finite element simulation of high -speed cutting forces［J］.Journal of Materials Processing Technology，2006，176:117 -126.

［3］Özel Tugrul. The influence of friction models on finite element simulations of machining［J］. International Journal of Machine Tools ＆ Manufacture，2006，46:518 –530.

［4］Childs T H C. Friction modelling in metal cutting［J］. Wear，2006，260:310 –318

［5］Lin Z C，Lin Y Y. A study of oblique cutting for different low speed［J］.Journal of Materials Processing Technology，2001，115:313 -325.

［6］Moufki A，Dudzinski D，Molinari A，et al. Thermoviscoplastic modelling of oblique cutting:forces and chip flow predictions［J］. International Journal of Mechanical Sciences，2000，42:1205 -1232.

［7］吕明，郭建英. 刀-屑摩擦对斜角切削切屑流动特性影响的仿真研究［J］. 兵工学报，2010，31(11):1491 -1497.

［8］周大隽. 锻压技术数据手册［M］. 北京:机械工业出版社，1998:61 -64.