考虑喷注流强分布的纵向稳定性建模与分析

2021-07-07汪广旭谭永华陈建华庄逢辰洪流陈宏玉杨宝娥

航空学报 2021年6期

汪广旭，谭永华，陈建华，庄逢辰，洪流，陈宏玉，杨宝娥

1. 西安航天动力研究所液体火箭发动机技术重点实验室，西安 710100

2. 航天推进技术研究院，西安 710100

3. 航天工程大学宇航科学与技术系，北京 101416

燃烧不稳定问题几乎伴随着液体火箭发动机的整个研制历程[1-4]，也是现役型号发动机面临的最大威胁。液体推进剂的燃烧涉及喷注、雾化、蒸发、混合以及化学反应等多个子过程，其高频燃烧不稳定的形成本质上是这些子过程与燃烧室内各种类型扰动之间形成的非线性耦合振荡，其中涉及复杂的湍流、多相流、超临界流动、非线性声学、化学反应等过程，是该领域研究面临的主要挑战。

通过喷注器面流强的非均匀分布来直接或间接改变燃烧室内的横向和轴向燃烧分布，是除阻尼装置以外，使发动机稳定工作的一种重要工程方法。一般认为，喷注器面附近是稳定性的敏感区域。对于横向振型，此区域内横向波动容易与推进剂喷雾燃烧过程耦合，进而激发振荡。喷注器径向流强分布能使主燃烧区尽量避开径向和切向振型波腹区，并且由此导致的横向不均匀性也不利于横向波动的传播，从而起到了抑制横向振荡的作用。对于纵向振型，喷注器面是一阶纵向声振波腹区，燃烧过于集中或靠近该区域能够最大程度地补充热声耦合所需的能量，不利于稳定。喷注器径向流强分布能够使推进剂沿轴向燃烧分布更加均匀，最大限度地减少波腹区燃烧释热量，降低热声耦合的强度，进而有利于纵向稳定。

NASA[1]曾针对不同流强分布的燃烧室进行了实验研究，其研究结果表明：喷注器径向“陡驼峰”形流强分布在爆炸弹引发的扰动下能稳定工作。为了消除研制初期推力室高频纵向燃烧不稳定问题，中国FY-20发动机[2]在改进的S方案中通过增加“驼峰区”流强的方式使能量释放沿燃烧室轴线较均匀地分布，从而抑制了高频纵向燃烧不稳定问题。考虑到结构及热防护等方面的因素，某现役上面级常温自燃推进剂液体火箭发动机推力室单纯采用“驼峰形”流强分布的方式来抑制其横向和纵向振荡。在最近的几次试车过程中，该发动机推力室出现了与燃烧室一阶纵向声振频率一致的燃烧不稳定现象，并且表现出了明显的随机性。根据非线性系统动力学理论，该发动机推力室处于稳定性边界附近[5]，其纵向稳定性裕度较低，需要引起足够的重视。

经验表明：高的燃烧效率会导致出现燃烧不稳定的风险增加，在不明显降低发动机性能的前提下提高稳定性裕度存在一定难度。此外，该发动机采用自击互靠式喷注器，喷注流强主要通过调整喷注孔径的方式来实现。由于各圈喷嘴的流量孔径均不同，任何细微的改变都可能会引起发动机性能和稳定性发生较大的变化。因此，需要建立考虑“驼峰形”流强分布的稳定性分析模型，能够对其振荡抑制特性进行详细的分析，避免因提高稳定性裕度而造成发动机性能的降低。

在这一方面，以全物理过程解析为目标的数值仿真方法仍是该领域主要的研究方向之一，尤其是近年来，在大推力、高室压、可重复使用液氧/烃发动机研制背景下，以AVBP[6]为代表的一些软件或代码在液体推进剂跨临界燃烧流场仿真方面取得了重要进展。理论模型方面，以Flandro等[7-8]提出的能量平衡方法为代表的非线性理论模型在揭示燃烧室压力振荡过程的非线性行为方面取得了一定的进展。为了在型号研制过程中实现快速设计迭代，工程上目前仍普遍采用半经验半解析的理论模型，后者大都通过降阶或线化的方式建立起来，结合大量试车数据，这些理论模型往往能够给出合理的预测结果。较为典型的是NASA在20世纪90年代开发的ROCCID[9-10]代码，该代码至今仍是国内外相关研究机构的重要工具，并且仍在不断改进和完善。

然而，现有的燃烧不稳定性分析模型中，能够考虑流强分布或多喷嘴情况的不多。庄逢辰[11]在自燃推进剂液滴蒸发模型和多流管耦合模型的基础上，建立了适用于撞击式喷注器的发动机性能及稳定性分析模型，其中采用多喷嘴、不同粒径液滴蒸发50%位置的平均值作为纵向稳定性评价参数，为早期常温自燃推进剂液体火箭发动机的研制提供了重要的参考。本文在上述工作的基础上，针对液滴蒸发作为燃烧速率控制过程的情况，拟建立一种基于液滴蒸发模型和三维热声不稳定模型相结合的考虑喷注流强分布的高频纵向燃烧稳定性分析模型。

1 基本原理

1.1 高频纵向集总燃烧模型

目前，针对液体火箭发动机高频纵向不稳定问题,应用最为广泛的工程分析方法是Crocco和Cheng[12]提出的基于敏感时滞理论的高频纵向集总燃烧模型，其原理如图1所示。该模型假设燃烧集中发生在燃烧室某个特定的轴向位置Ψ(集中燃烧锋面)，锋面前后燃气质量流率的变化量采用压力敏感时滞模型给出，并用波动方程描述燃烧锋面后扰动的传播过程。之后，Casiano[13]利用自动控制原理，建立了开环传递函数形式的集总燃烧模型，并进一步引入了喷注导纳、喷管阻抗以及系统耗散效应等。作者团队[14]采用改进后的集总燃烧模型对某型发动机燃气发生器缩尺件高频纵向燃烧不稳定性进行了分析，验证了系统耗散对模型预测精度的影响。

图1 集总燃烧模型

虽然集总燃烧模型并不能用来揭示燃烧释热与振荡之间的详细耦合机理，但在大量试车数据的基础上，该模型可以定性或半定量地给出发动机改进前后稳定性的预测趋势。经过多年的发展，集总燃烧模型已成为工程上分析和预测高频纵向燃烧稳定性的重要方法，并已被ROCCID等采用。

然而，集总燃烧模型在分析考虑喷注流强分布的高频纵向不稳定性时存在2点不足：① 对高频纵向不稳定问题十分关键的集中燃烧位置只能作为经验参数给定，无法与实际喷注条件建立联系，无法考虑不同喷嘴对应集中燃烧区沿轴向分布的情况；② 零维波动方程无法考虑喷嘴的空间分布特性，无法针对多个燃烧响应函数条件下的稳定性进行分析，限制了模型分析范围。因此，需要在集总燃烧模型的基础上，进一步改进，拓展其工程应用范围。

1.2 拓展思路

一般认为，对于液滴蒸发作为燃烧速率控制的情况，不易挥发组元液滴的蒸发过程决定了燃烧的特征时间[1-2]，后者通常与燃烧响应(以压力敏感型为例)所需的时滞τ有关。因此，液滴蒸发是建立此类高频燃烧不稳定问题分析模型的重要基础。在这一方面，Priem、Heidmann和Sirignano等都曾开展过类似的研究，例如，Delplanque和Sirignano[15]在集总燃烧模型的基础上，结合液滴蒸发模型，详细讨论了氧的跨临界蒸发响应对低温推进剂发动机纵向稳定性的影响。

此外，对于采用液滴蒸发作为燃烧速率控制的情况，蒸发所需的时间远大于液体推进剂其他燃烧子过程所需的时间，不易挥发组元液滴的蒸发过程还决定了推进剂燃烧释热的轴向分布，蒸发速率峰值位置Ψe可以近似代替集中燃烧位置Ψ。液滴蒸发的初始粒径可以由雾化公式给出，后者与喷注器类型、孔径、推进剂流量、温度等喷注条件有关。这样，采用Ψe的集总燃烧模型可以将实际喷注条件与稳定性之间建立联系，具有实际工程意义。

燃烧室声学方面，三维频域线化欧拉方程(Linearized Eular Equation，LEE)已能够在短时间内求解，并在近年来热声不稳定方面的研究中得到了广泛的应用。例如，Sun等[16]采用三维热声不稳定分析方法讨论了周向非均匀性对高频纵向振荡的影响；Gutmark等[17]采用类似的方法研究了加力燃烧室的燃烧不稳定问题；Schuermans等[18]基于预混火焰传递函数建立了环形燃烧室的热声不稳定性控制模型；Tamanampudi和Anderson[19]建立了多喷嘴条件下的高频切向燃烧不稳定分析模型。

集总燃烧模型采用压力敏感时滞模型来描述推进剂燃烧释热对压力振荡过程的响应。但严格讲，对于液滴蒸发作为燃烧速率控制的情况，当燃烧室内发生高频燃烧不稳定时，敏感时滞τs应至少是组元液滴蒸发、混合和化学反应3个子过程时滞的总和[2]，且相对于压力扰动，液滴蒸发过程对燃烧室内速度扰动更为敏感。然而，目前还缺乏速度敏感的相互作用指数n和时滞τs的相关经验数据，还无法提供一个较为完整的速度敏感型燃烧响应。此外，对于液滴蒸发作为燃烧速率控制过程，可以近似忽略蒸发后的混合过程，假设不易挥发组元蒸发后即进行化学反应释热。因此，本文仍近似采用基于压力敏感时滞τs和相互作用指数n的燃烧响应来分析缩尺燃烧室的相对稳定性。其中，自燃推进剂压力敏感时滞τs可以采用Harrje和Reardon的经验关系式[1]给出，其表达式为

(1)

式中：Mae为喷管入口马赫数；pc为室压；C′、b为常数；di为喷注孔径。

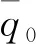
综上，本文在集总燃烧模型的基础上，拟采用三维频域线化欧拉方程描述燃烧室波动过程，采用自燃推进剂雾化及液滴蒸发模型计算不同喷嘴对应的集中释热区位置，并在各集中释热区采用相互独立的压力敏感时滞燃烧响应函数，从而建立考虑喷注流强分布的高频纵向燃烧稳定性分析模型。在此基础上，针对某常温自燃推进剂液体火箭发动机推力室缩尺件“驼峰形”流强分布的稳定性抑制特性进行分析。

2 问题描述

某常温自燃推进剂液体火箭发动机推力室的缩尺实验件如图2所示。与实际推力室一致，该缩尺实验件采用自击互靠式喷注器，喷注流强主要通过调整喷注孔径的方式来实现。燃烧室室压为4.43 MPa、混合比为2.3，远低于燃料偏二甲肼(C2H8N2/UDMH)和氧化剂四氧化二氮(N2O4/NTO)的临界压力，两组元液滴始终处于亚临界蒸发状态，液滴蒸发是推进燃烧的速率控制过程。

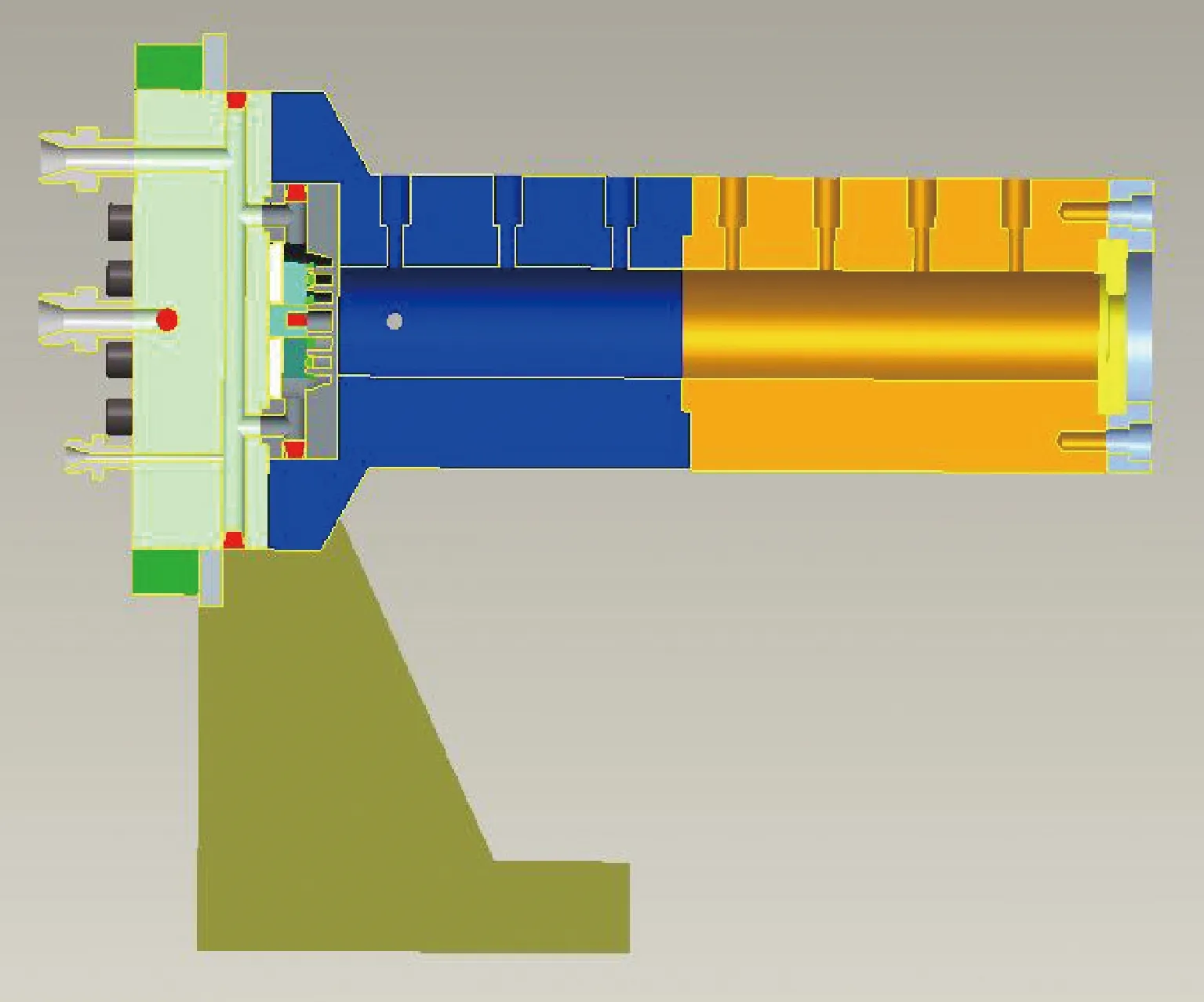
图2 缩尺燃烧室

经过再生冷却后的氧化剂入口温度可以达到98 ℃，相应室压下NTO的离解度[20](如图3所示)可以达到30%，且NTO的饱和蒸汽压较肼类燃料高，可认为该工况下NTO较UDMH蒸发快得多。因此，在对缩尺燃烧室的分析中，近似忽略氧化剂的蒸发过程，单纯以UDMH液滴的蒸发过程作为稳定性分析的基础。

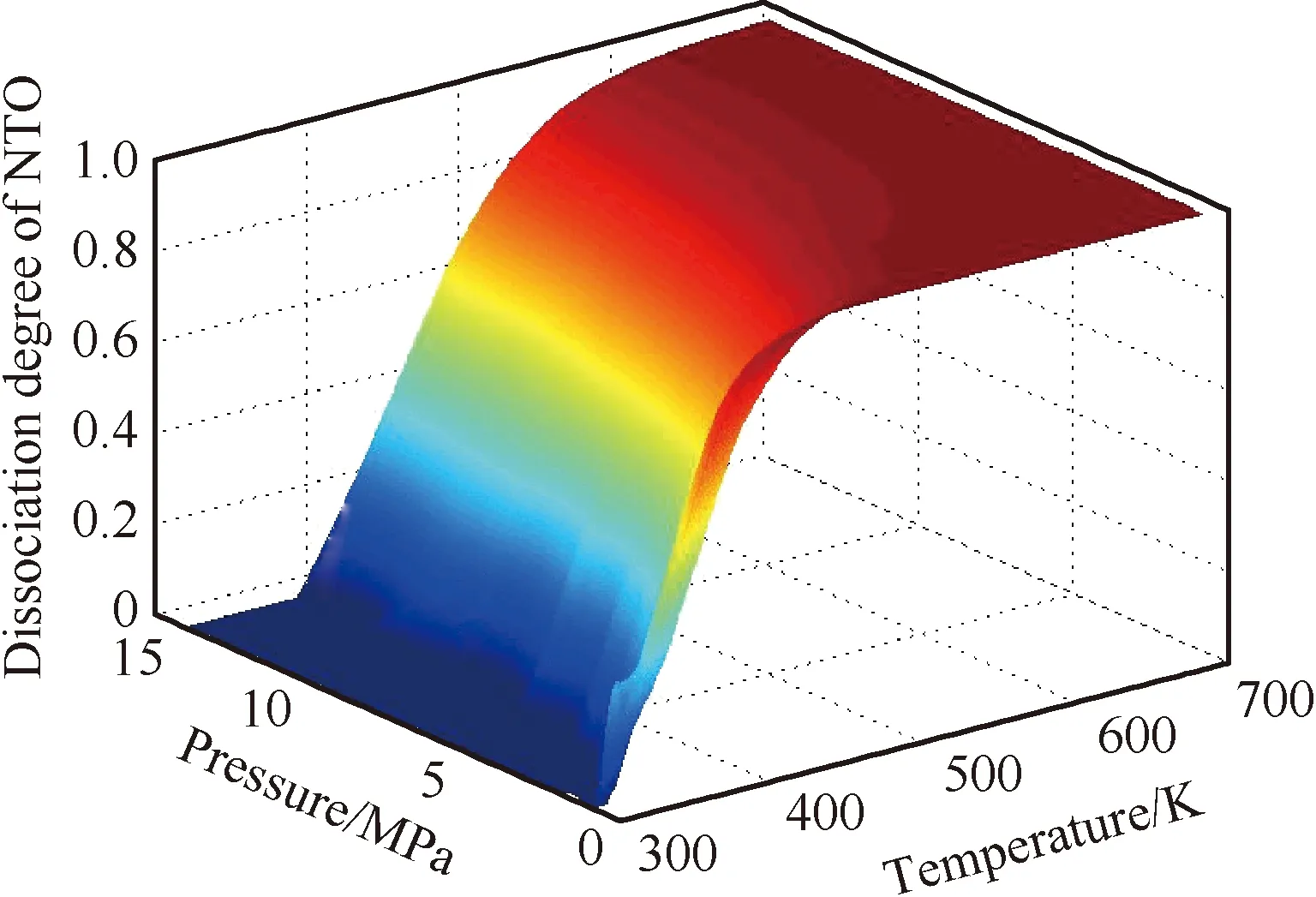
图3 NTO离解度

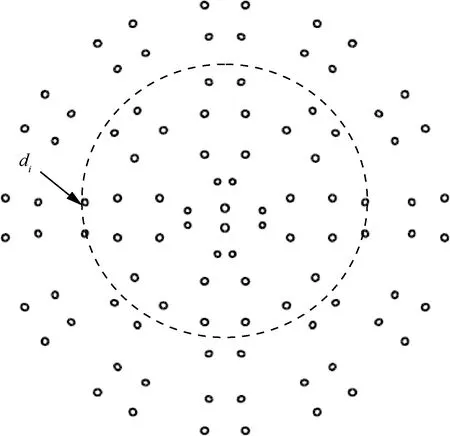
图4 喷嘴分布

(2)

式中：D0为缩尺燃烧室内径；Di为第i圈喷嘴分布圆直径。

除了中心一对自击喷嘴以外，第2、5、6圈均为燃料喷嘴，且由内向外分布圆直径Di分别为8 mm、 30 mm和40 mm，其余为氧化剂喷嘴。这样，第2和3、4和5、6和7圈喷嘴分别构成了径向3个主燃烧区(1、2、3)，各燃烧区流强I的定义与式(1)类似，其中，流量为燃料和氧化剂流量之和。

缩尺燃烧室采用了独立可拆卸喷注器，10个喷注流强分布方案下各燃烧区燃料喷嘴孔径di如图5所示，相应的流强I分别如图6所示。其中，P0-0、P0-1、P0-2、P0-3为第1组对比工况，3区燃料喷嘴孔径和流强依次增加；P0-0、P1-0、P1-1、P1-2为第2组对比工况，2区燃料流强依次增加，即形成径向“驼峰形”流强分布特征；P0-0、P2-0为第3组对比工况，1区燃料流强依次增加；P0-0、P3-0、P4-0为第4组对比工况，3个区域流强基本保持一致，但相对P0-0，P3-0工况整体降低了燃料喷注孔径，P4-0整体增加了燃料喷注孔径。上述所有工况下，各主燃烧区的混合比保持不变，因此燃料流强也可近似代表该区推进剂总流强的大小。

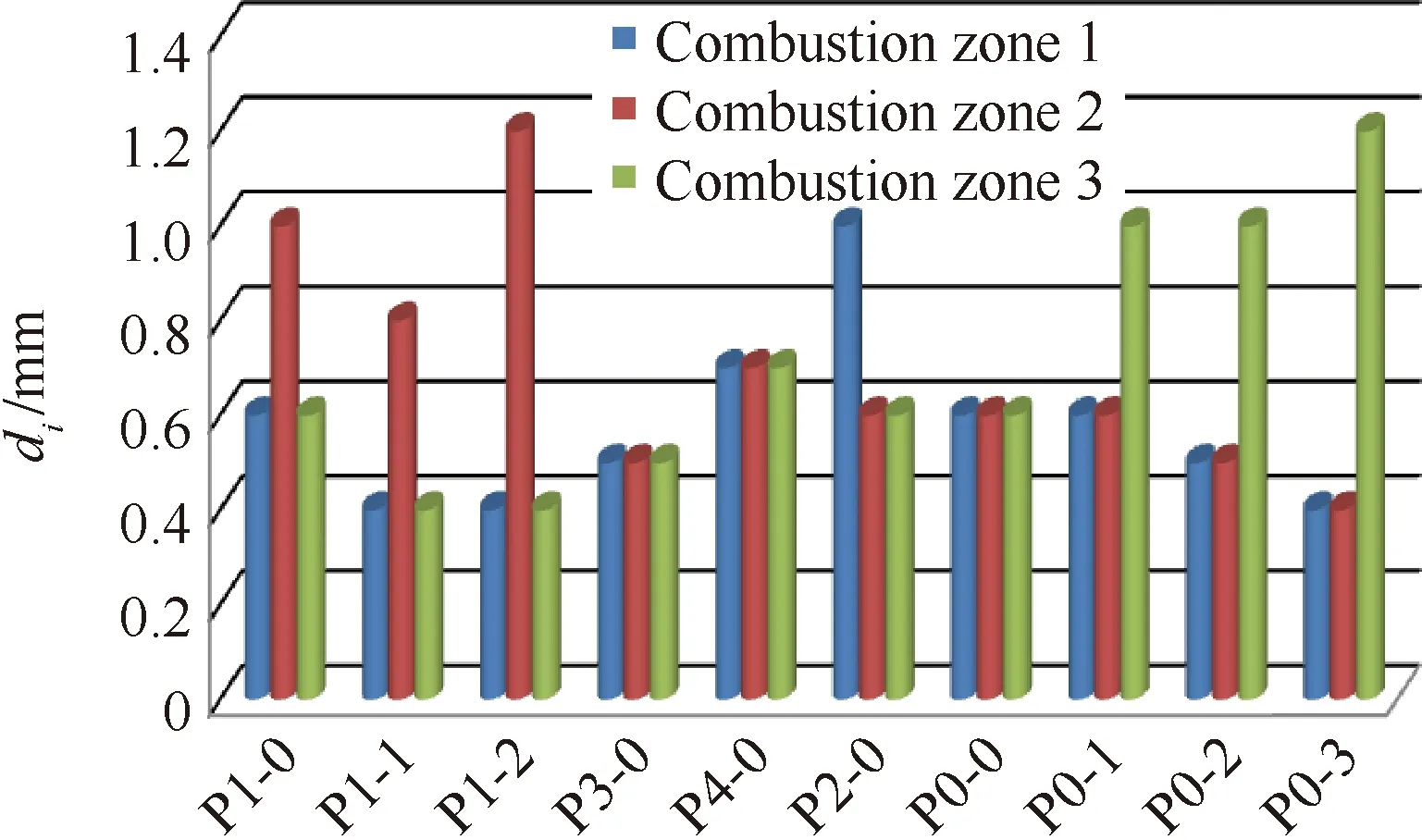
图5 喷注孔径分布

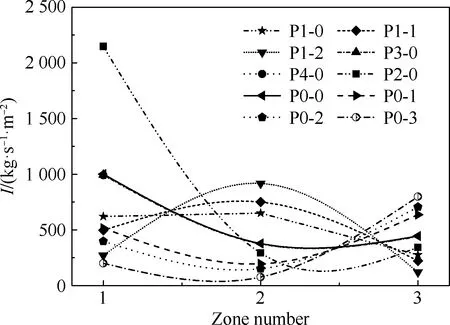
图6 喷注流强(燃料)分布

(3)

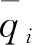
3 理论模型

3.1 稳定性模型

在不考虑非线性效应的前提下，燃烧室内扰动传播特性可以采用以下LEE方程进行描述[19]：

(4)

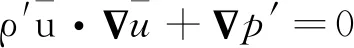
(5)

(6)

式中：x和t分别为空间和时间变量；p、ρ、u、c分别为压力、密度、速度和声速；q为源项(时域)；γ为比热比；上标“-”和“′”表示平均量和脉动量。

假设扰动满足以下时空分离形式：

(7)

式中：上标“^”表示空间分量；ω的实部代表了特征频率，虚部代表了该模态频率信号的增长率，可以用来代表燃烧室内该频率信号对应声模态的稳定性。将式(7)代入到式(4)～式(6)可得以下频域线化欧拉方程：

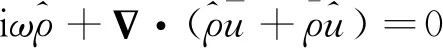
(8)

(9)

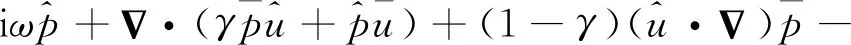
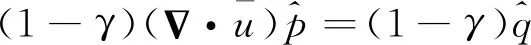
(10)

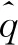
(11)

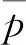
3.2 液滴蒸发

虽然缩尺燃烧室压力较UDMH的临界压力低，但仍需要考虑高压的影响。这一方面，庄逢辰[11]提出的高压液滴蒸发模型具有明确的物理概念，计算量相对较小且准确度高，方便应用于工程实际。与非自燃推进剂不同，在一定的压力和温度下，UDMH液滴存在自分解放热反应，生成热的分解燃烧产物反过来又会加速液滴的蒸发，其物理模型如图7所示(图中T和r分别为温度和径向位置)。在此基础上，聂万胜和庄逢辰[22-23]根据层流火焰传播理论，通过液滴表面蒸发出来的蒸汽向火焰锋流动的速度等于层流火焰传播速度这一主要条件，建立了绝热和非绝热条件下分解火焰锋处的层流火焰传播速度，从而建立了自燃推进剂液滴的高压蒸发模型。以下是对该模型的简单描述。

组分守恒：

(12)

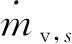
(13)

其中：

非绝热条件下中间量An的推导过程及具体形式见文献[12]，最终得到非绝热分解反应峰处的温度Tf和半径rf的表达式为

(14)

式中：Tf,a和T∞分别为绝热分解反应火焰峰温度和环境温度；r∞为折算薄膜半径；Cp,v和Cp,e分别为液滴表面蒸汽比热和环境气体比热；Cp,I和Cp,II分别为图7中I区和II区混合气体比热；λII为II区混合气体导热系数，近似认为Cp,II和λII与环境气体相同，后者由化学热力学平衡软件(CEA)计算得到。

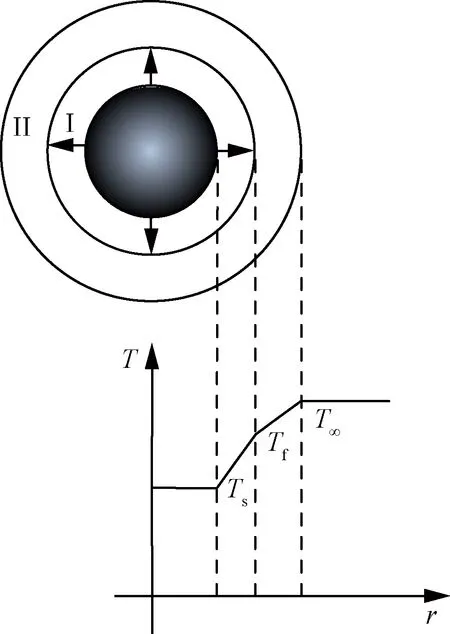
图7 肼类推进剂液滴蒸发计算模型

能量守恒：

(15)

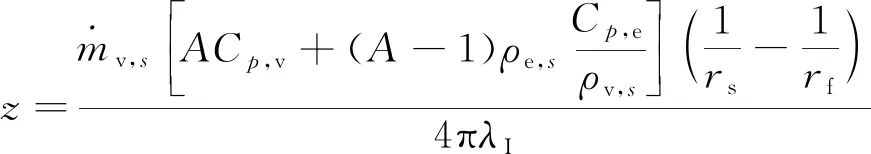
(16)

式中：λI为I区导热系数；qd为传给液滴的热量。假定液滴内部温度均匀，由热平衡方程可以得到：

(17)

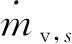
3.3 液滴运动方程

液滴轴向速度的变化是气动阻力作用的结果，根据牛顿第二定律可以写出：

(18)

式中：u和V分别为燃气和液滴速度；ρg为燃气密度；CD为阻力系数，由于液滴有变形，所以阻力系数不符合斯托克斯定律，其值可按以下方式选取：

已知雷诺数Re后，可以用来更新液滴的对流努塞尔数Nu，具体表达式为

Nu=2+0.556Re0.5Pr1/3·

(1+1.237Re-1Pr-4/3)-0.5

式中：Pr为普朗特数。在此基础上，可以计算液滴蒸发过程中的折算薄膜半径r∞，具体形式为

r∞=rsNu/(Nu-2)

这样，可以评估液滴与燃气之间的对流对自燃推进剂液滴蒸发过程的影响。

3.4 喷雾模型

为了将实际喷注条件与稳定性之间建立联系，本文引入了两股自击式喷注器的喷雾模型，其雾化平均粒径普遍采用Ingebo公式[24]。庄逢辰[11]采用该公式对常温推进剂发动机FY-20进行效率计算，取得了与实验一致的结论。但Ingebo公式并未考虑推进剂物性的不同、环境压力的变化以及撞击角的改变。庄逢辰[11]建议对自燃推进剂二股直流自击式喷注单元采用以下计算公式：

(19)

式中：α为修正系数；dj为喷注单元射流直径，一般等于喷注孔径di；uj和ug分别为液滴射流速度和燃气速度，后者需要根据液滴局部蒸发情况确定；K为考虑推进剂物性的修正系数；ρact为燃烧室燃气密度；ρref为空气密度。

4 结果分析

4.1 液滴蒸发过程

为了获得较为可信的燃烧轴向分布，首先需要对UDMH喷雾及蒸发过程进行分析讨论。根据上述模型，在已知燃烧室压力、混合比的条件下，可以根据CEA计算得到相应的环境物性参数；在已知燃料喷注孔径、喷注流量和速度的条件下，可以根据式(18)得到燃料雾化后的质量平均粒径d30之后，根据式(11)～式(17)计算缩尺燃烧室内UDMH液滴沿轴向的蒸发过程。高压条件下，上述UDMH液滴蒸发模型所需的物性参数，包括饱和蒸汽压、密度、比热、导热系数以及黏度等都需要考虑高压下真实流体状态方程以及相应的混合规则，本次计算分别采用了SRK方程和Chung方法[20]。

首先，对不同燃料喷注孔径di下UDMH蒸发过程进行分析。图8给出了di在0.77～1.21 mm范围内(基本涵盖了实际推力室的主要喷注孔径分布范围)，缩尺燃烧室中UDMH液滴蒸发速率沿轴向的分布规律，其中，液滴初始雾化距离为25 mm。可以看到，在距离喷注面大约4.2～5.6 cm 的距离内，液滴UDMH液滴达到了蒸发速率的峰值位置Ψe，但在开始雾化后的很短距离内，蒸发速率会经历一个低谷。这是由于液滴初始喷注速度较喷注面附近的燃气速度要高，但随着蒸发的进行，燃气速度会不断增加，液滴在燃气阻力的作用下速度减小，液滴与燃气之间的速度差会在某一位置等于零。此时，流动对液滴蒸发的影响最小，相应的UDMH液滴蒸发速率也达到了最小值。

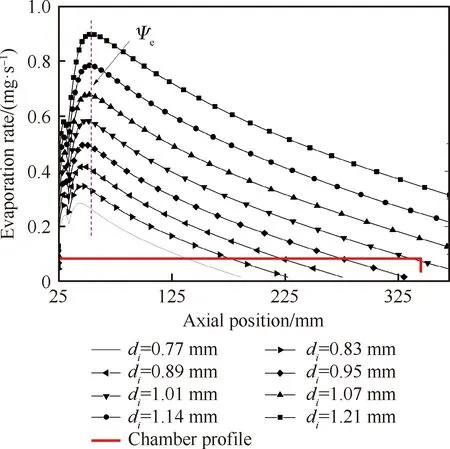
图8 不同喷注孔径下液滴蒸发速率的轴向分布

图8给出了一个明确的结果，即随着喷注孔径di的增加，液滴蒸发速率峰值位置Ψe更远离喷注面。然而，在燃料流量不变的情况下，喷注孔径的增加实际伴随着喷注速度的降低，后者带来的结果是液滴远离喷注面的速度放缓，从而使蒸发速率峰值位置Ψe靠近喷注面。显然，di的增加带来的上述2种结果理论上是矛盾的，意味着喷注孔径的单独改变对于蒸发速率峰值位置Ψe的影响并非是线性的。图9的结果进一步证实了上述结论，其中给出了蒸发速率峰值位置Ψe随喷注孔径的变化规律。虽然总体上，蒸发速率峰值位置Ψe随着di的增加而增加，但两者的关系并非是完全单调线性的，在di=1.02,0.81 mm处，增加di反而会导致Ψe的降低。这说明在所给缩尺燃烧室工况下，平均喷注孔径在以上两点附近时，增加孔径、降低喷注速度有可能会导致燃烧区更靠近喷注面。

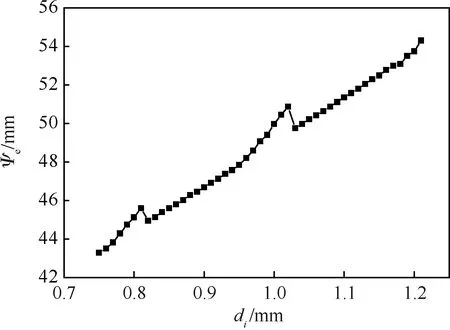
图9 蒸发速率峰值位置Ψe随喷注孔径di的变化规律

4.2 集中释热条件下的稳定性

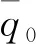
根据缩尺燃烧室各圈喷嘴喷注孔径di及工况参数，由式(1)可以得到相应的敏感时滞范围τs=0.1T1L～0.2T1L(T1L为一阶纵向声模态频率信号的周期)。图11给出了敏感时滞τs=0.1T1L和τs=0.2T1L条件下，增长率α1L随Ψ的变化规律。根据Stow和Dowling[25]的研究结果，热源的加入会使最终的热声耦合频率偏离燃烧室自然频率，但由于偏离幅值相对较小，本文近似忽略了上述影响，即满足图10所示振型分布对应的频率都认为是一阶纵向声学频率f1L。可以看出，随着集中释热位置Ψ的增加，增长率α1L呈下降趋势，意味着随着集中燃烧区远离喷注面时，高频纵向稳定性降低。如果近似采用蒸发速率峰值位置Ψe代替集中燃烧位置Ψ，由4.1节分析可知，喷注孔径di与Ψ之间的关系并不是绝对线性，即喷注孔径的增加或减小并不一定会导致相应的高频纵向稳定性增强或减弱。以上分析结果与Abbe等[26]的研究结论一致，即喷注孔径的增加对纵向稳定性的改善并不绝对。

图10 稳定性分析模型及一阶纵向声模态

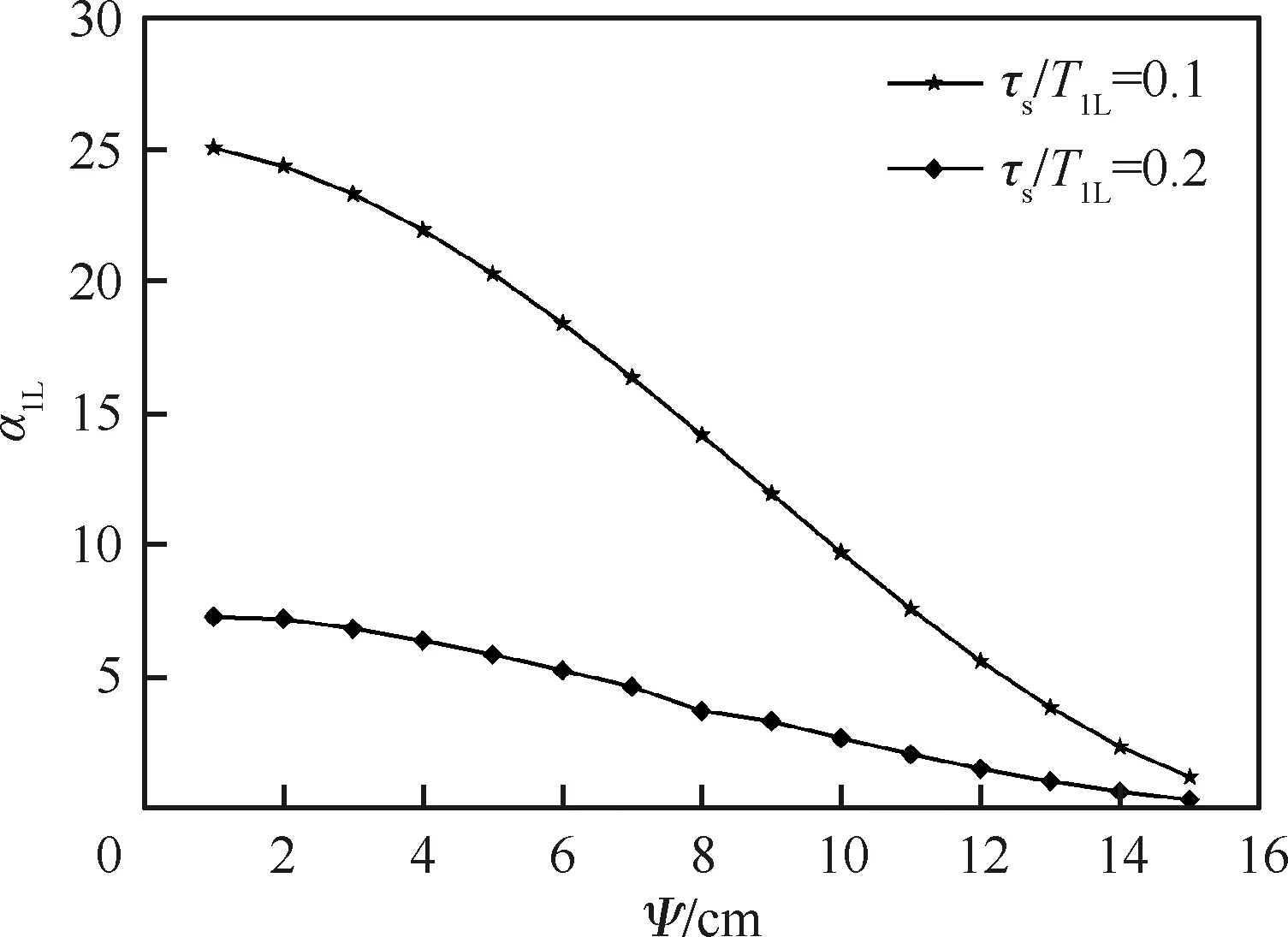
图11 增长率随Ψ的变化规律

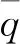
4.3 考虑喷注流强分布条件下的稳定性

考虑实际情况时，各圈喷嘴的集中释热位置仍然可以采用相应喷注孔径di对应质量平均粒径下液滴蒸发过程来确定。实际考虑喷注流强的纵向稳定性计算流程如图12所示。在已知各燃烧区的燃料喷注孔径di的情况下，根据雾化模型求出平均液滴粒径，在已知液滴初始温度Td和喷注速度Uj的条件下，根据蒸发模型求解液滴蒸发过程。其中，液滴环境气体参数(包括环境气体温度Te、比热比γ、导热系数λ、黏度μ等)近似采用燃烧室平均燃气参数，后者由CEA计算得到，并最终获得各燃烧区的集中释热位置。由NASA经验关系式(1)给出敏感时滞和相互作用指数，由式(3)给出各燃烧区平均释热量。在此基础上，建立燃烧响应源项，并采用4.2节的方法构建多喷注条件下的稳定性分析模型。

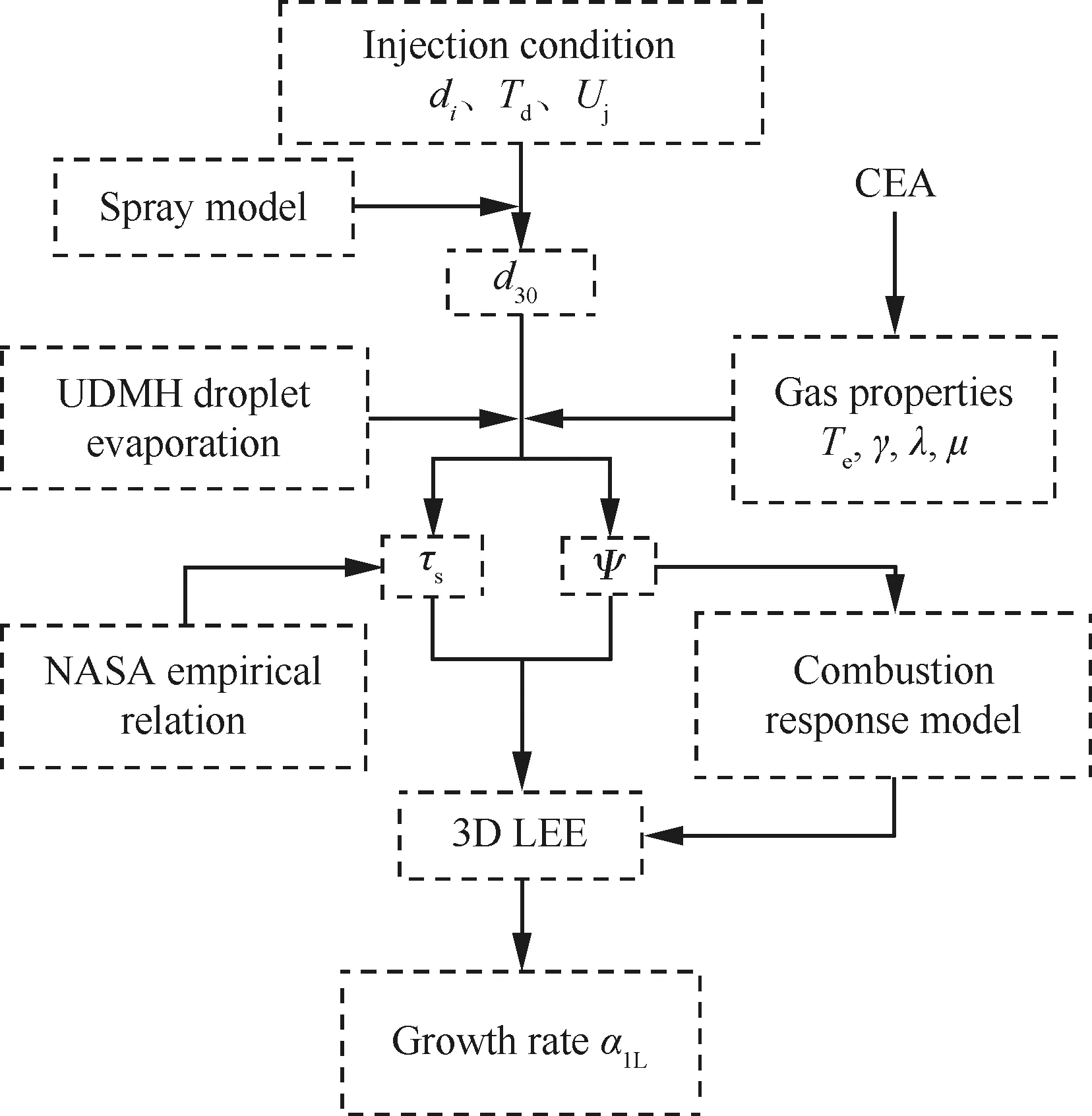
图12 分析流程

图13 考虑喷注流强分布的一阶纵向稳定性分析模型

图14给出了各工况增长率的对比结果，结合图5和图6可以看出，对于第1组对比工况，随着3区流强的增加，一阶纵向声模态信号对应的增长率呈下降的趋势，一方面得益于喷注孔径的增加，使集中释热区远离喷注面，另一方面得益于3区流量的增加。然而，相对P0-1，P0-2工况保持了3区的喷注孔径，降低了1区和2区喷注孔径，但其增长率反而要低于P0-1。这是由于P0-2工况下3区在孔径不变的情况下，流量增加，进而增加了下游燃烧区的释热量，因此稳定性反而要好于P0-1工况。

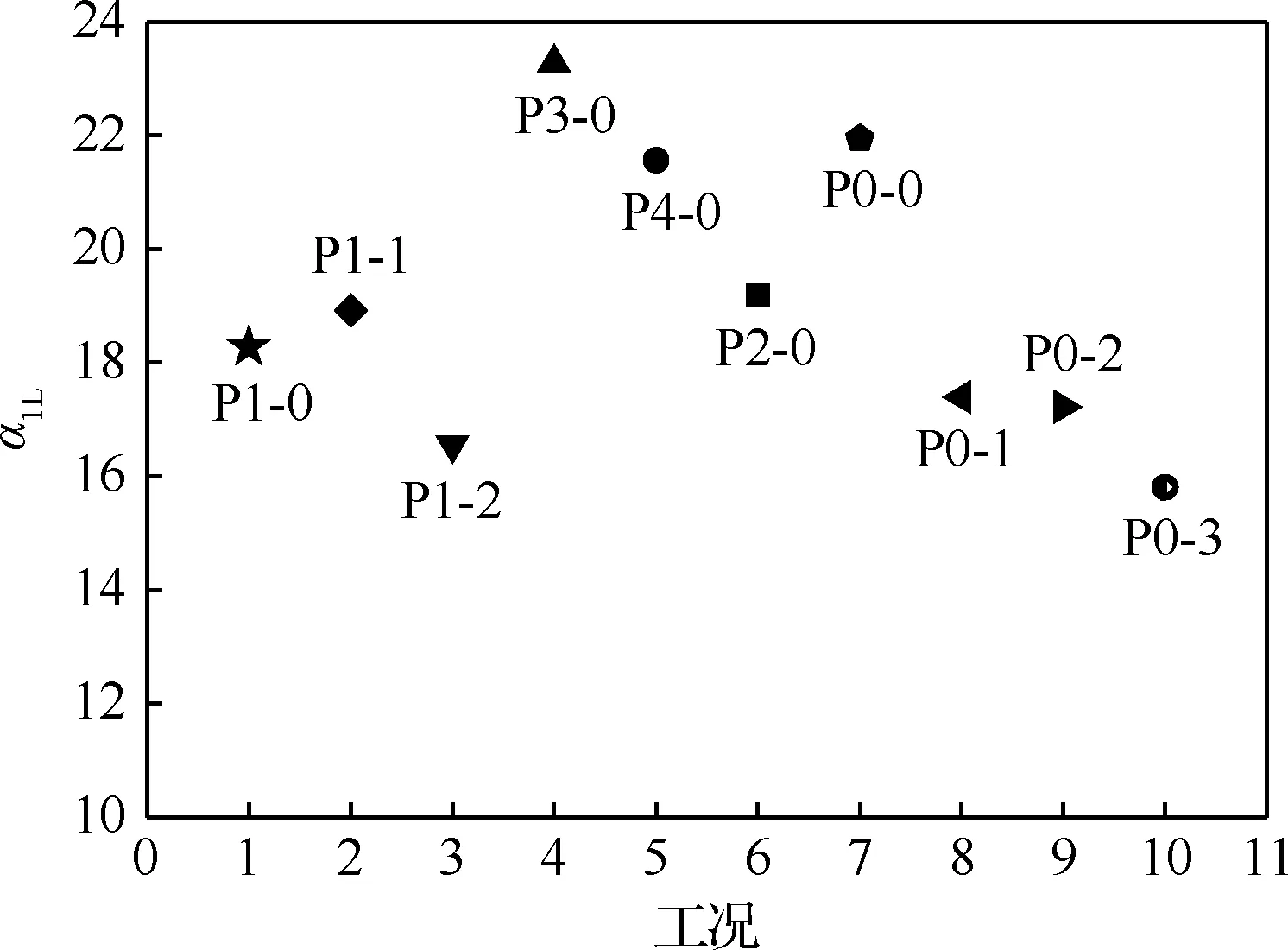
图14 各工况增长率对比

对于第2组对比工况，随着“驼峰区”流强的增加，P0-0、P1-0、P1-1、P1-2的增长率并没有单调递减，P1-1的增长率较P1-0的增长率要大。这是由于，虽然P1-1工况2区的流强较P1-0的大，但前者2区燃料喷注孔径较后者要小，燃烧更靠近喷注面。以上结果说明，实际喷注流强的增加对稳定性的改善并不是绝对的，还需要兼顾喷注孔径的大小。以P1-2和P1-1工况为例，“驼峰区”流强增加30%，相应一阶纵向声振信号增长率降低15%。

第3组对比工况表现出了和第1组对比工况类似的趋势，即随着1区流强的增加，P2-0工况稳定性得到了改善。对于第4组工况，虽然喷注流强相同，但P0-0、P3-0、P4-0仍然表现出了不同的稳定性，总体上增加喷注孔径的P4-0工况增长率较低，稳定性较好。

此外还可以看出，采用统一喷注孔径的第4组工况整体上较其他各组工况的增长率要高、稳定性要差。将第4组工况与P1-1工况对比可见，即使后者1区和3区燃料喷注孔径较小，但P1-1的增长率较低，这一结果证明了流强分布对于抑制纵向不稳定的重要意义。P2-0和P0-1采用了相反的孔径分布，但两者工况存在差异，这主要是由于1和3区的流量不同，相应的平均释热率存在差异。

综上，纵向稳定性对于喷注流强的改变十分敏感，孔径的细微差异都可能造成稳定性显著变化，在优化喷注流强分布以提高稳定性时，应综合考虑各圈喷嘴流量占比以及孔径，尽量保证流量占比高的主要燃烧区远离喷注面，优先考虑增加该区的喷注孔径。